Zenn
ZENKIGENテックブログPublicationへの投稿
🚉

station2vec: 関東の横浜駅は関西の神戸三宮駅？ GNNを用いた駅の埋め込み表現の学習

redtea
2023/10/24に公開
AI
機械学習
PyTorch
GNN
embedding
tech

はじめに

こんにちは。ZENKIGENデータサイエンスチーム所属のredteaです。原籍はオムロンソーシアルソリューションズ株式会社 技術創造センタですが、社外出向でZENKIGENに所属しており、数理最適化や機械学習を用いたデータの分析業務をしております。

本記事でやること

本記事では、タイトル "station2vec" の名の通り[1]、Graph Neural Network (GNN)を用いて、

駅の埋め込み表現を3次元で可視化すると、以下のようなイメージです。このように、駅の特徴を視覚的・定量的に把握することが目的です。

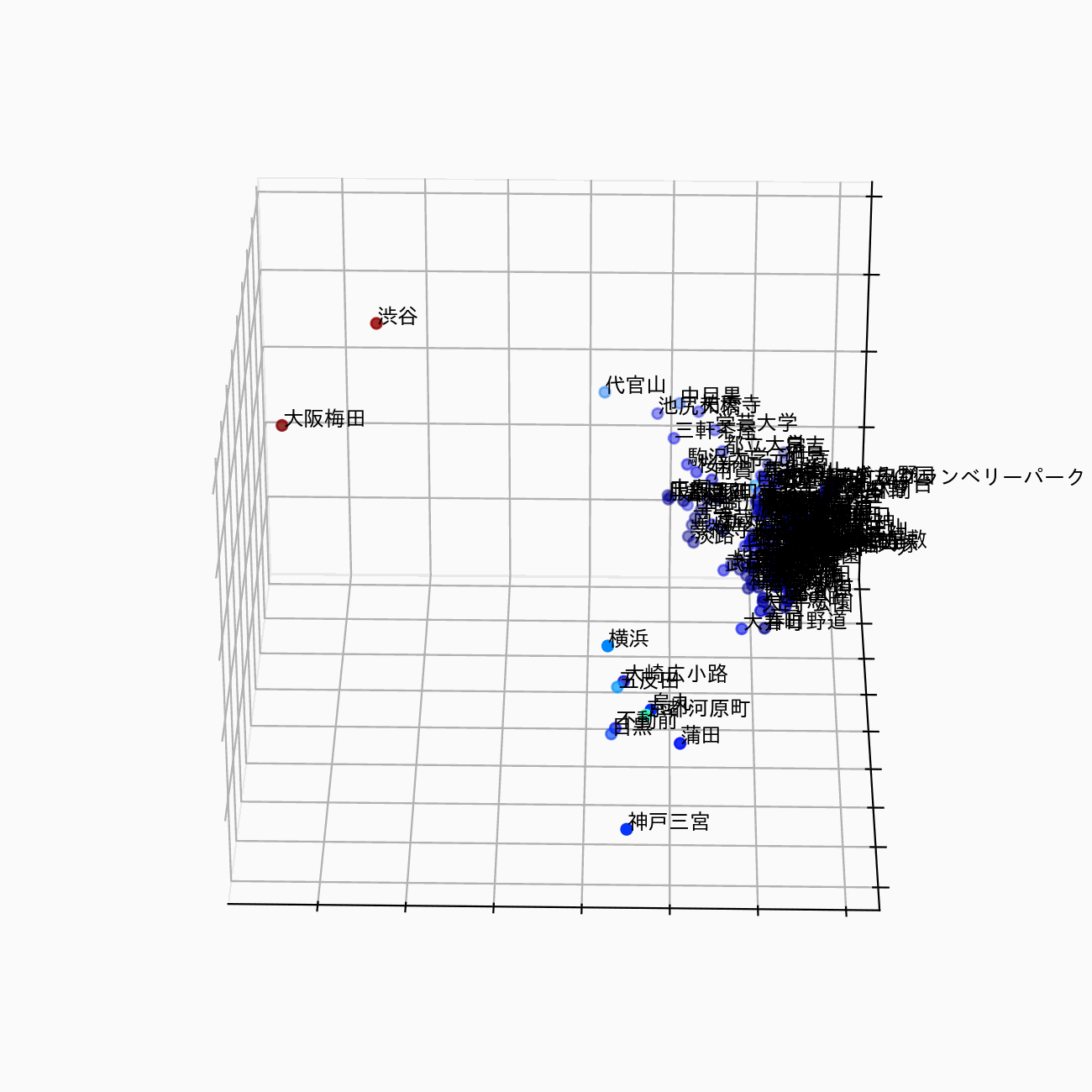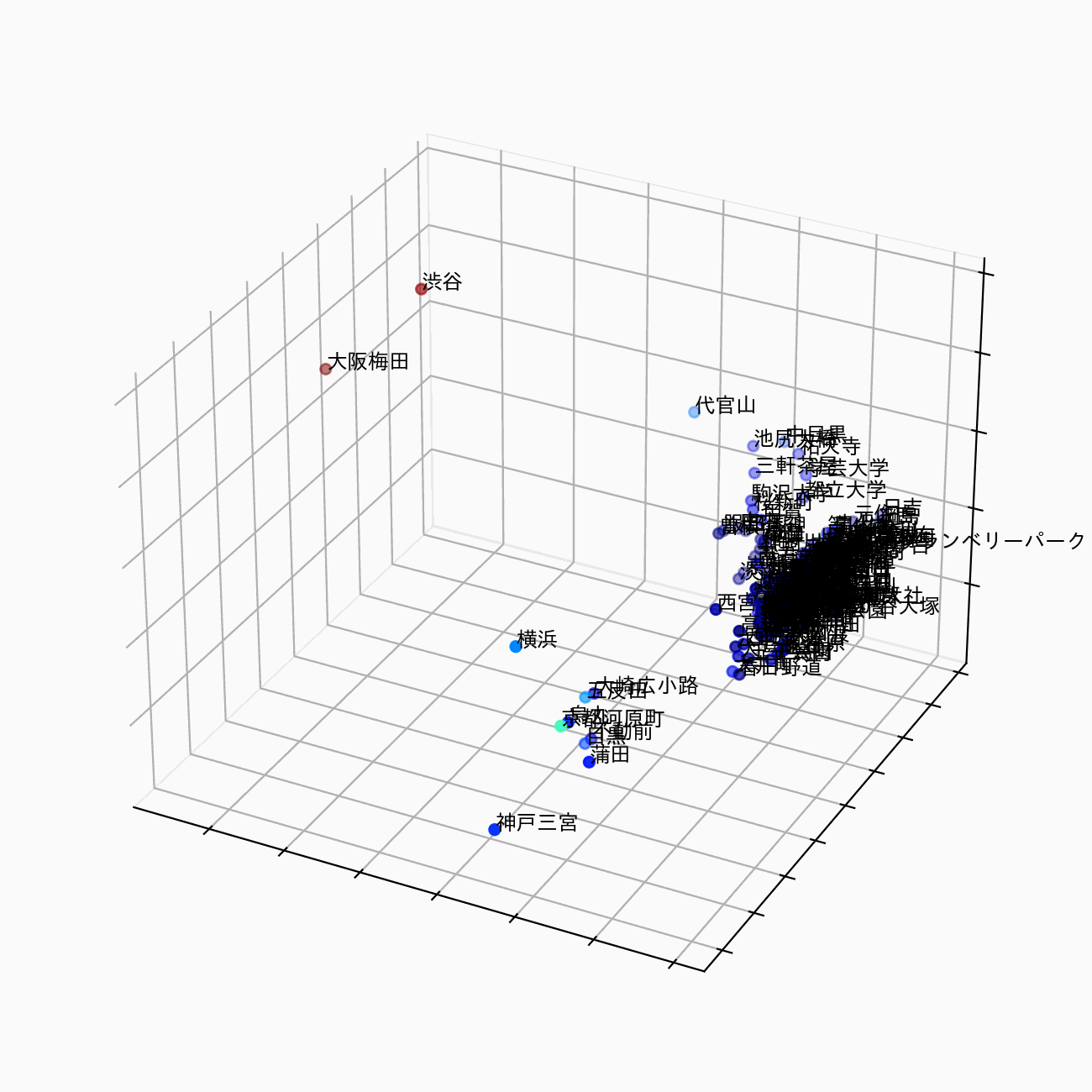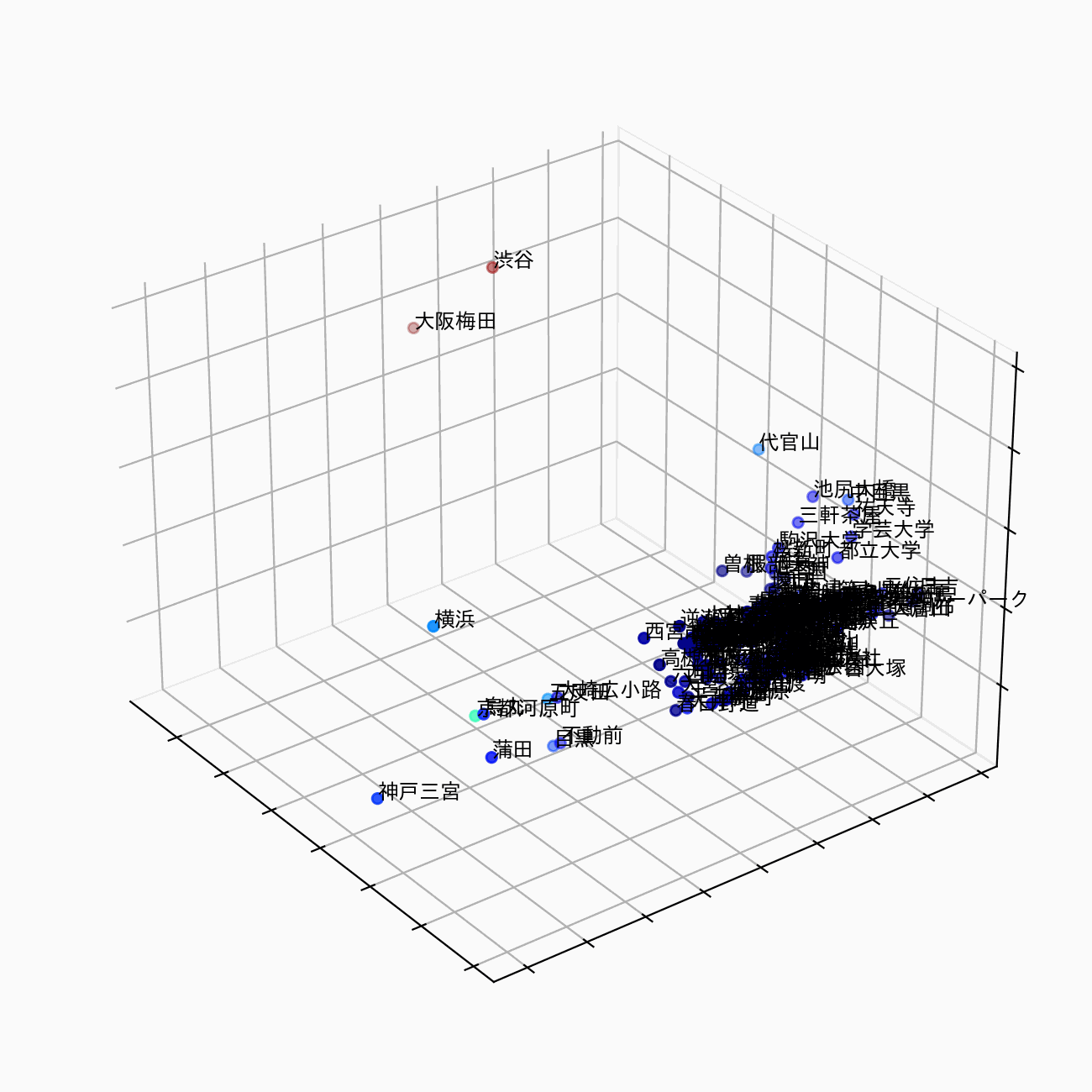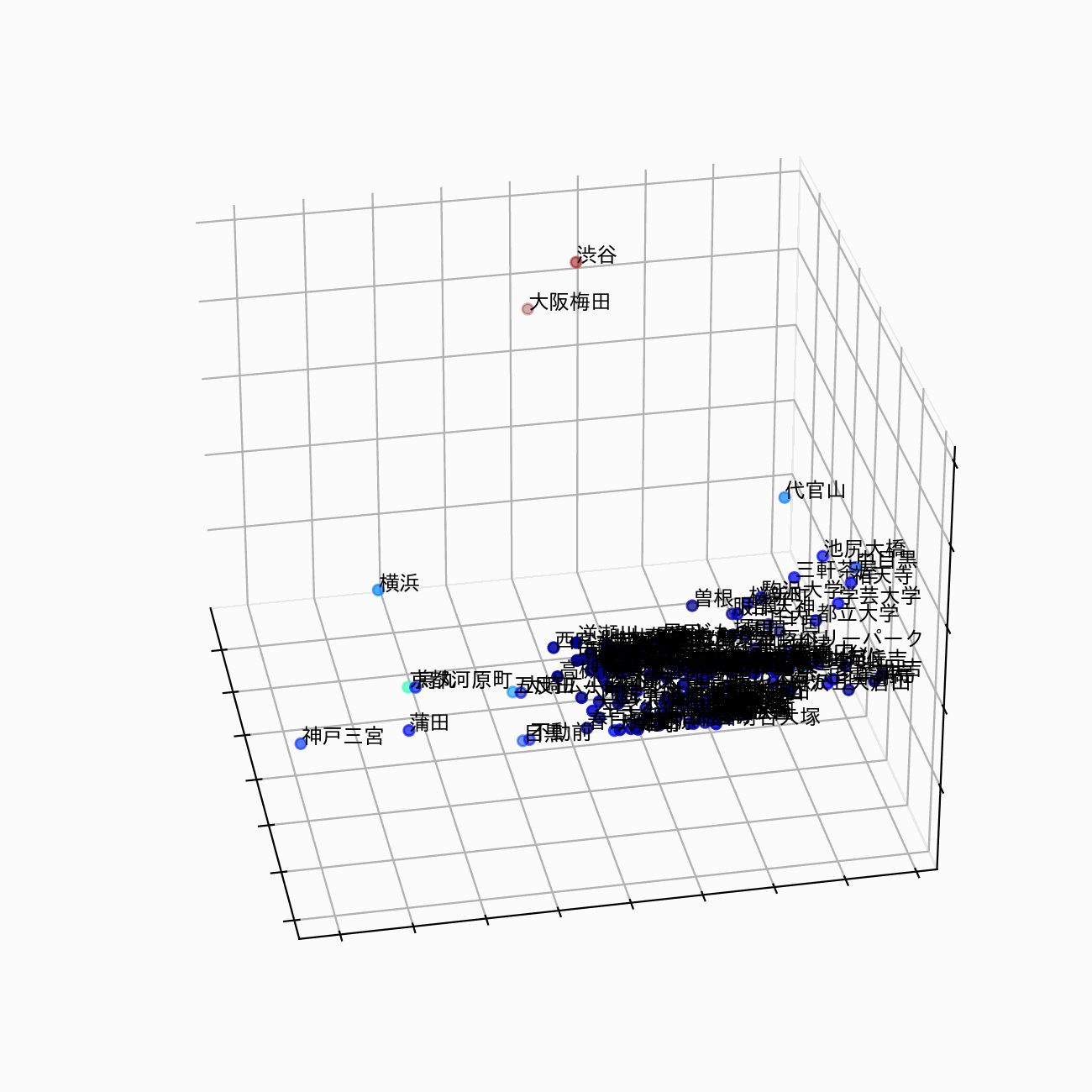
3d-station-vector
駅の埋め込み表現 (station2vec) のイメージ

駅の埋め込み表現は、以下のように活用できます。

  • 慣れ親しんだ駅と似た駅を探すことができる
  • 事業者がイベントの開催地を決める時の判断材料の一つにできる

例えば関西出身者が土地勘のない関東に異動する際、慣れ親しんだ地元と似た駅で、新たな住まいを探すようなことができるようになるかもしれません。また、イベント事業者が、過去にA駅でイベントを開催して大成功した場合には、A駅と似ている駅でも同様のイベントを開催すると成功する可能性が高いかもしれません。

本記事で実装した駅の埋め込み表現を用いた「似ている駅を検索できるサービス」をGitHub Pages を用いて公開していますので、以下のリンクから是非遊んでみてください！

https://atsushi-green.github.io/station2vec/

筆者のモチベーション

個人的な話ですが、筆者はGNNs というグラフ構造を持つデータに対してニューラルネットワークを適用する技術が好きです[3]。GNNsを解説している記事の多くでは、「そもそもグラフとは何か」の説明から始まり、そのグラフ例として、道路交通網、SNSの友人関係、化学式の構造、論文の引用被引用、そして鉄道路線図が紹介されています。しかし、鉄道路線図を用いたGNNsの応用例を私はあまり見かけません。そこで、GNNsを鉄道路線図に適用する応用例を作ってみようと思いました。

また、私自身が関西から関東に引っ越した経験があるので、関西の地元でXX駅に住んでいて気に入っているから、XXに対応する関東の駅周辺に住みたい！を実現できればと思っています。

前提 (似ている駅とは)

「関西のXX駅は関東のYY駅」を実現するにあたって、似ているとはどういう状況かを定義する必要がありますが、これは非常に難しいです。基本的には学習時に与えるデータが似ていれば、似ている駅となるので、どんなデータを与えるかが、どんな駅同士を似ていると定義するのと同等だと考えています。

例えば、

  • 駅周辺の様子が似ていれば似ている(オフィス街 or 住宅街 or 繁華街)
  • 都心までの所要時間が同じだから似ている
  • 近くにある施設が似ているから似ている(半径500m以内に大学・海・病院・有名な神社・ブランドショップがある)

などなど、様々な定義やデータが考えられますし、先行研究(?)では、生ビールの平均価格と、飲食店の料理ジャンルなどを元にしたデータを用いた例もありました。

https://sirabee.com/2014/07/04/780/

できるだけ多種多様なデータを与えることでより面白くなる一方、それだけ時間と労力がかかってしまうことと、どんなデータを入れるかが恣意的[4]になってしまうので、今回は「似ている」の定義をあえて曖昧なまま進め、最低限取得しやすいデータのみを利用した結果を見て、当たっていたり当たっていなかったりして楽しむという逃げ気味のスタンスでやっていきたいと思います。実際に使ったデータは、「利用データ」章で説明します。

GNNsについて

概要

GNNs や、そもそもグラフとは？ については、多数の解説記事がありますので、ここでの概説は控えさせていただきます。私が分かりやすいと感じた記事を1つ紹介しますので、以下のリンクからご参照ください。私もこの記事で学びました。

https://zenn.dev/kami/articles/83c2daff760f5d

Graph Convolutinal Network (GCN)

今回はGNNsの中でも、Graph Convolutinal Network (GCN)というものを利用するので、これだけは簡単に解説させていただきます。

GCNは、グラフ上で畳み込み演算を行います。CNNとGCNのイメージを以下の図に示します。
図左をご覧ください。画像処理でお馴染みのCNN(Convolutional Neural Network)は、あるピクセルに対して、フィルタサイズに応じたその周辺のピクセル情報を加味するような処理をします(畳み込み演算)。これをグラフに拡張したものがGCNです（下記図の右）。赤色になっているノードに対する畳み込み演算は、そのノードと隣接するノードの特徴量にCNNの重みフィルタに相当する重み行列をかけたものを集約することで定義されます。すなはち、画像では、「隣接するピクセル間には何らかの関係性がある」という考えを、グラフでは「エッジにより隣接するノード間には何らかの関係性がある」というアイデアに拡張したものと直感的に解釈できます。

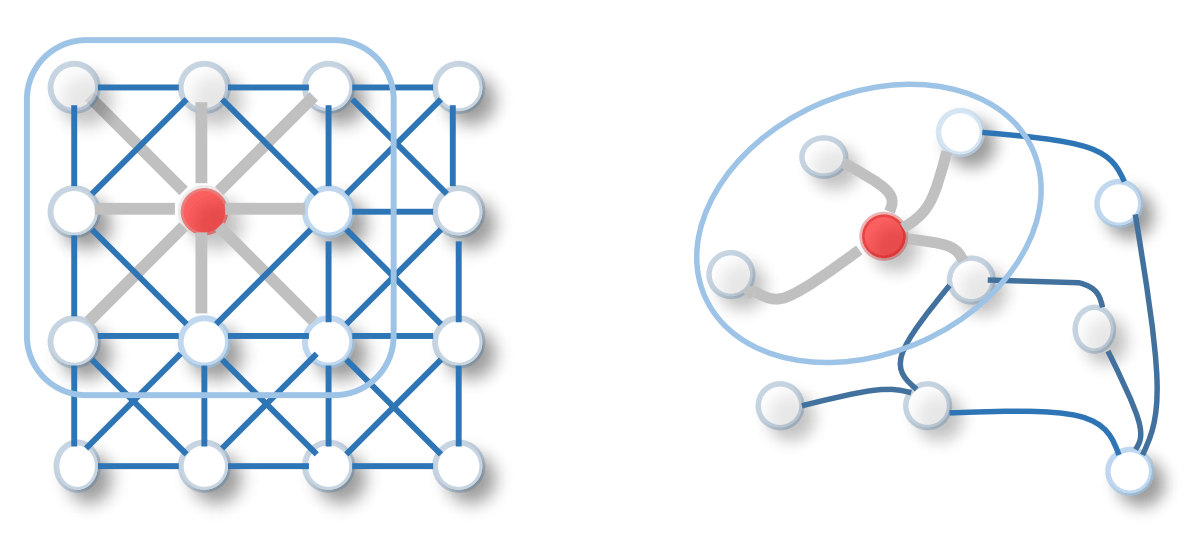
cnn_gcn
左右それぞれがCNN, GCNのイメージ。A Comprehensive Survey on Graph Neural Networks Fig. 1 より引用。

GCNのアイデアを見ると、隣接するノードの特徴しか畳み込めないように思ってしまいますが、GCN層を多層化することでより遠くにあるノードの特徴量を加味することができます。確かに1層目のGCNでは、あるノードに隣接したノードの特徴しか加味できませんが、2層目では、その隣接するノードもさらに隣の隣接ノードの特徴を畳み込んでいるので、結果として、2つ隣のノードの情報も含めることができます。すなはち、層の深さ分だけ、離れたノードの特徴量を加味することができます。

GCNの問題点

駅の路線図のようなグラフ構造では、例えば20個隣のノードのような、離れたノード間にも関係性があると考えられます[5]。前節の、「層の深さの分だけ遠くのノード特徴量を加味できる」ことから、単純に20個ものGCN層を用意すれば良さそうですが、実は単に多層化すると neighbor explosion (近傍爆発) や oversmoothing problem (過剰平滑化問題) といった問題が生じます。

neighbor explosion

GCNの層が深くなるにつれて、加味されるノードの数が指数関数的に増えていきます。次数[6]が高いノードが存在すると、そのノードへ畳み込むノード数が多くなり、計算量が増えてしまったり、次項で説明する oversmoothing problem にも繋がりやすくなってしまいます。駅の路線図では次数の高いノードは存在しないので、計算量の方は心配なさそうです。

oversmoothing problem

多層化により加味されるノードの数が増えていくと、多くのノードにおいて加味するノード特徴量が似通ってしまいます。イメージとしては、GCN層を重ねる度に、各ノードが発する特徴がグラフ全体に広がっていく感覚[7]です。このようにして、ニューラルネットワークの下流の隠れ層では、どのノードも似たような特徴ベクトルを持ってしまうことを oversmoothing problem と言います。これを軽減する1つの方法として、Initial Residual というテクニックがあります。これは入力特徴量ベクトルを各層に加えることで、下流でも入力特徴量を維持できるようにすることが狙いで、本記事でも採用しました。実装章で詳しく見ていきます。

手法

手法選定 (ノードの埋め込み表現の学習方法)

結論は、「Variational Graph Auto-Encoders を用いる。」です。本説ではその他のノード埋め込み表現の学習方法について触れながら、選定理由を説明します。

私が調べたところ、グラフ上のノードの埋め込み表現を学習させる方法は大きく以下の4種に分類できるように思います。

分類 手法例 概要
1. 一般的な次元圧縮 t-SNE, PCA グラフ構造に限らず次元圧縮できる
2. グラフ上を探索 Deep Walk, node2vec グラフ上を探索して、得られた文脈をskip-gramのように学習
3. ノードの繋がり方を利用 LINE ローカル、グローバルな近接性を定義し、グラフ構造から近接性を学習
4. グラフオートエンコーダー系 Graph Auto-Encoders, Variational Graph Auto-Encoders 入力特徴量を圧縮するエンコーダーと、圧縮された特徴量から入力特徴量を再出力するデコーダーにより学習

結論としてはオートエンコーダー系を採用しましたが、以下、それぞれの分類について簡単な解説と、採否の理由を述べます。

1. 一般的な次元圧縮

Principal Component Analysis (PCA) や t-Distributed Stochastic Neighbor Embedding (t-SNE) など、グラフ構造を使わない方法です。単純にノード特徴量を次元圧縮するだけです。せっかくのグラフ構造を使えないので今回は不採用にしますが、グラフ構造を扱う (GNNsを用いる) メリットを比較検証するために、対抗馬として利用します。

2. グラフ上を探索

グラフ上の隣接ノードをランダムに辿り、たどった道 (path) を自然言語における文と捉えます。その文に対してslip-gramアルゴリズム (word2vec でお馴染み) を適用することで、ノードの埋め込み表現を学習する方法です。Deep Walk, node2vec が代表例です。グラフの構造のみから埋め込み表現を学習することができるのが強みですが、ノードやエッジが持つ特徴量を考慮できないことと、関西の駅と関東の駅は路線図は繋がっておらずこれらの関係性を学習できないため、今回は不採用にします。

3. ノードの繋がり方を利用

ローカルな構造 (first-order proximity) と グローバルな構造 (second-order proximity) という2種類の近接性を定義し、近接性が高いノード同士がグラフ構造的に似ているとして、ノードの埋め込み表現を学習する方法です。LINE が代表例です。この2種類の近接性は以下の図で説明します。まず、ノード6とノード7は太い線で繋がっているので、似ていると判断されます(ローカルな構造)。また、ノード5とノード6はそれぞれノード1,2,3,4という同じノードと繋がっているため、似ていると判断されます(グローバルな構造)。この方法では、グラフ構造的に繋がっていなければ似ている駅とならず、「2. グラフ上を探索」と同様に、繋がっていない関西と関東の駅間での類似性が測れないので、不採用とします。

LINE
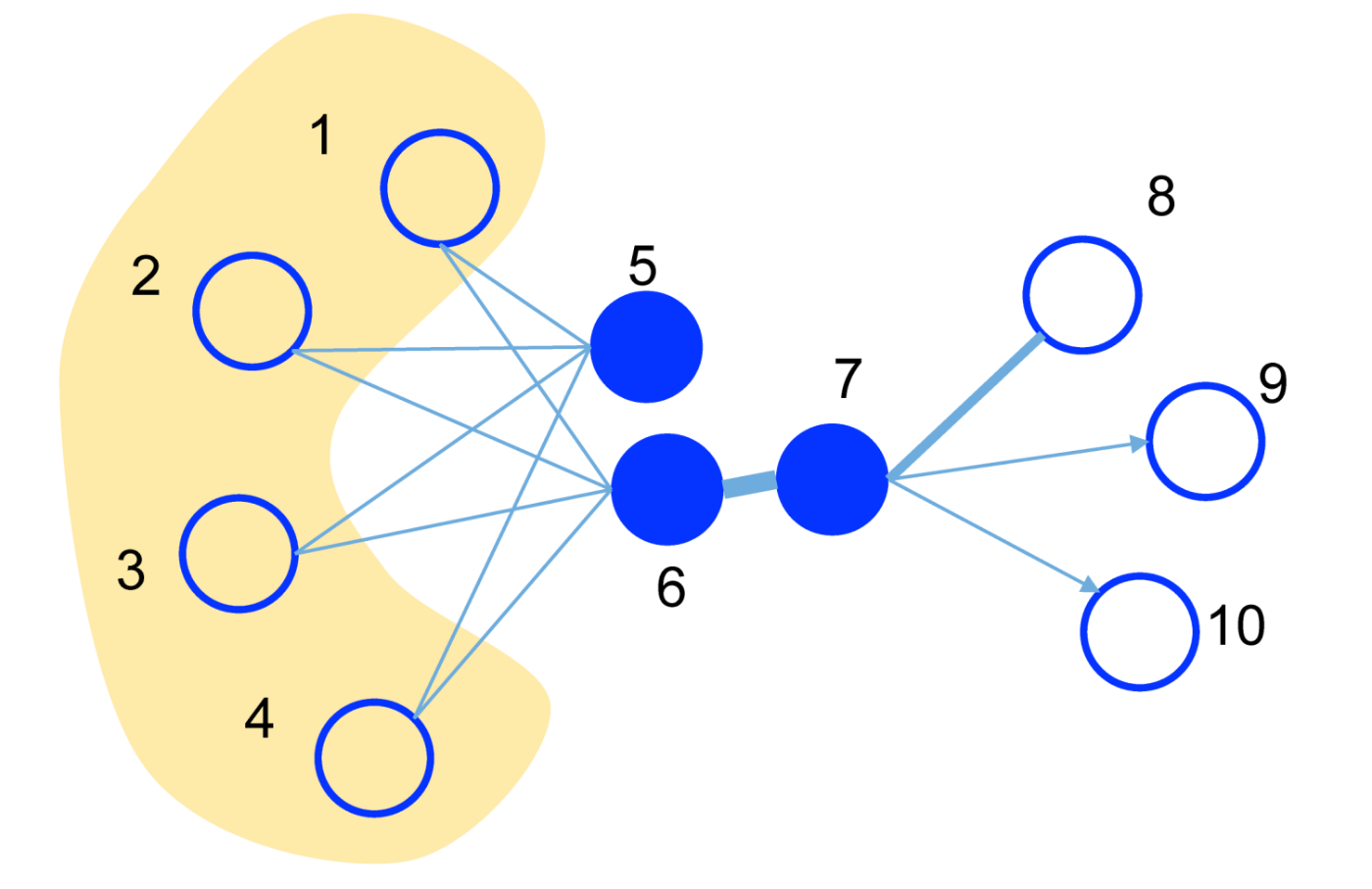
LINE: ローカルな構造とグローバルな構造の考え方 LINE: Large-scale Information Network Embedding Fig. 1 より引用。

4. グラフオートエンコーダー系

オートエンコーダーとは、ニューラルネットワークによって、入力特徴ベクトルと同じ特徴ベクトルを再現することで特徴量を抽出する手法です。グラフオートエンコーダー系では、ノード特徴量とエッジ特徴量を考慮でき、さらに Variational Graph Auto-Encoders を用いることで、埋め込み表現に正規分布を仮定でき、埋め込み表現を利用しやすいと考えたため、今回は Variational Graph Auto-Encoders を用いることにしました。

モデルアーキテクチャ

本節ではGNNを用いた駅の埋め込み表現の学習方法について説明します。

グラフの定義

駅をノードとしたグラフを構築します。そして、ノード間をエッジで繋ぐのですが、駅間は自由に行き来できるので、無向グラフとします。エッジの結び方は素朴に考えると路線図と同じように、隣り合う駅間だけを繋ぎたくなります（以下の東急路線図のように）。しかし、このようにグラフを定義してしまうと、GCNでは1層で1つ隣のノードの特徴量しか畳み込めないので、10個隣のノードの情報を加味するには10層のGCN層が必要になってしまいます。

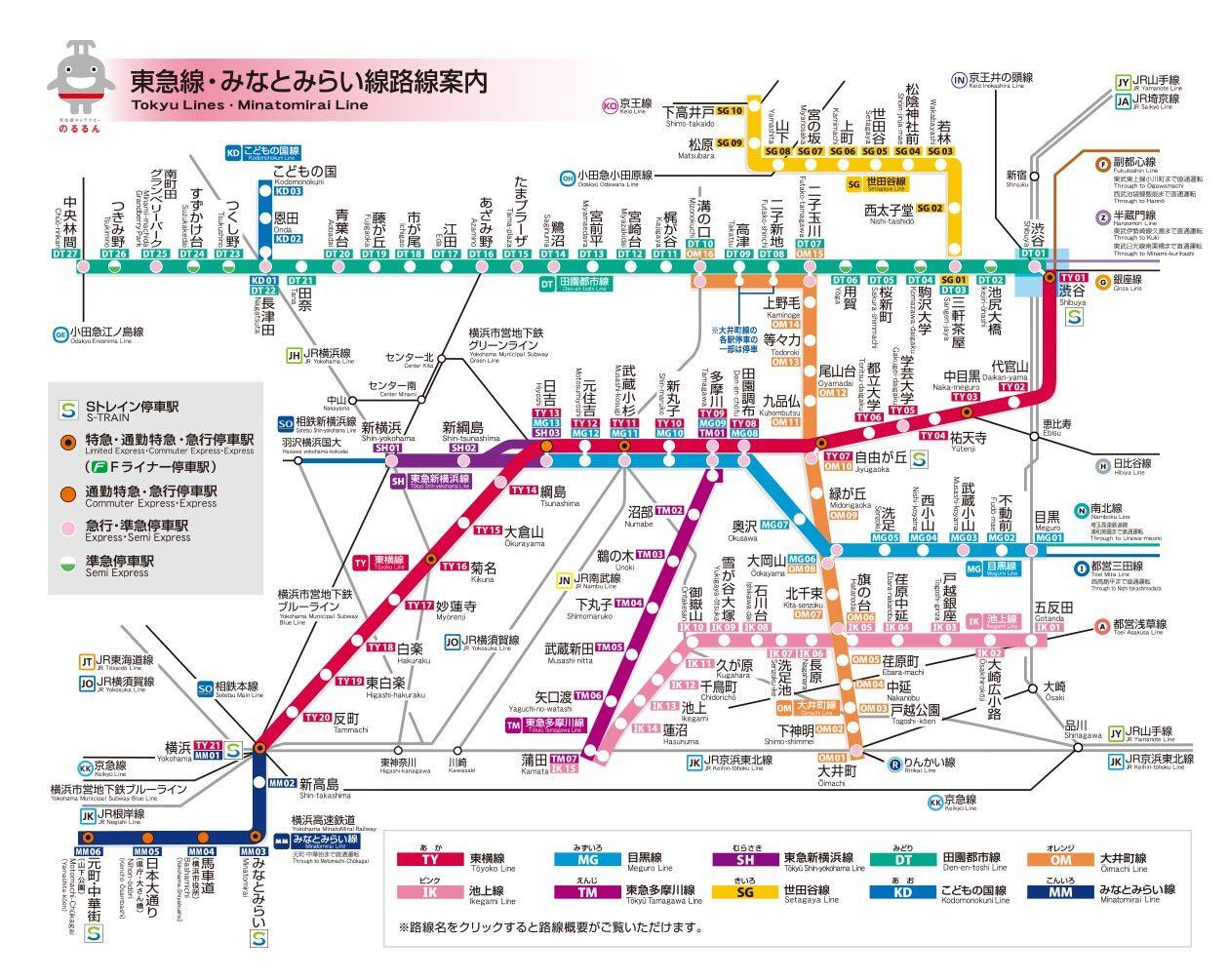
tokyu_rosenzu
路線図（マップ）. WEBサイト 東急株式会社 2023年8月30日参照. https://www.tokyu.co.jp/railway/station/map.html より引用)

そこで、路線図において、5つ隣の駅までをエッジで繋ぐ[8]ことにし、グラフ畳み込み層を4つ用意することで、最大20個[9]隣の駅の情報まで加味できるようにしました。また、自己ループ[10]も加えます。グラフ構造のイメージは以下の図の通りです（東急渋谷駅付近の池尻大橋駅と繋がっているエッジを抜粋しています）。

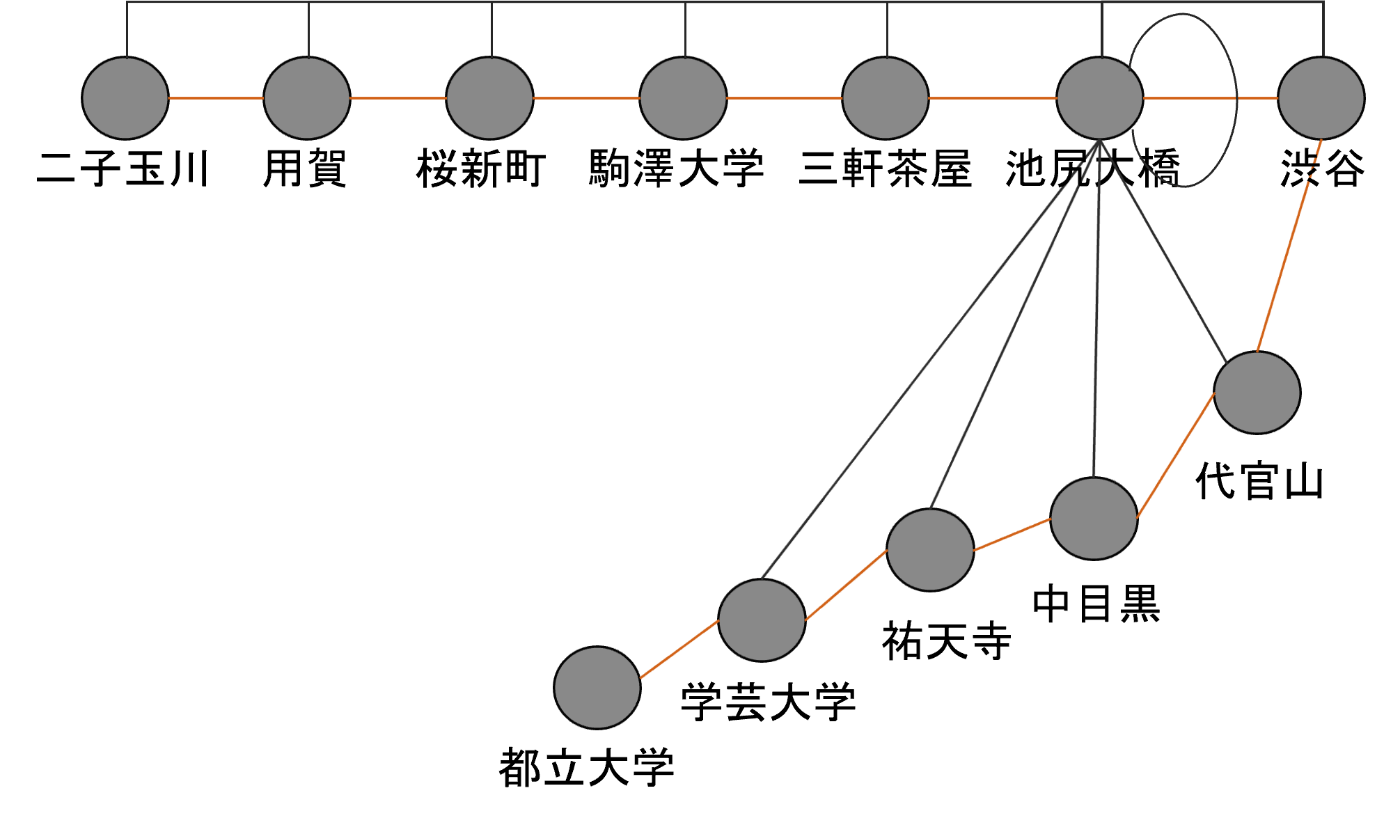
5_edge_graph
東急渋谷駅周辺の、池尻大橋駅のエッジの様子。自分自身へのエッジと、5つ隣の駅までエッジで結びます。オレンジの線は元々の路線図上でのつながりを表します。池尻大橋と都立大学は6駅隣なので、エッジで結ばれていません。池尻大橋から池尻大橋への自己ループもあります。

モデルの定義

以下の図のようなモデルを実装しました。グラフ畳み込みによってEncoderとDecoderを構築しています。図中のグラフ構造はあくまでもイメージで、隣のノード間しか結んでいませんが、実際は前項で決めた方法でグラフ構造を定義しています。

VGAE
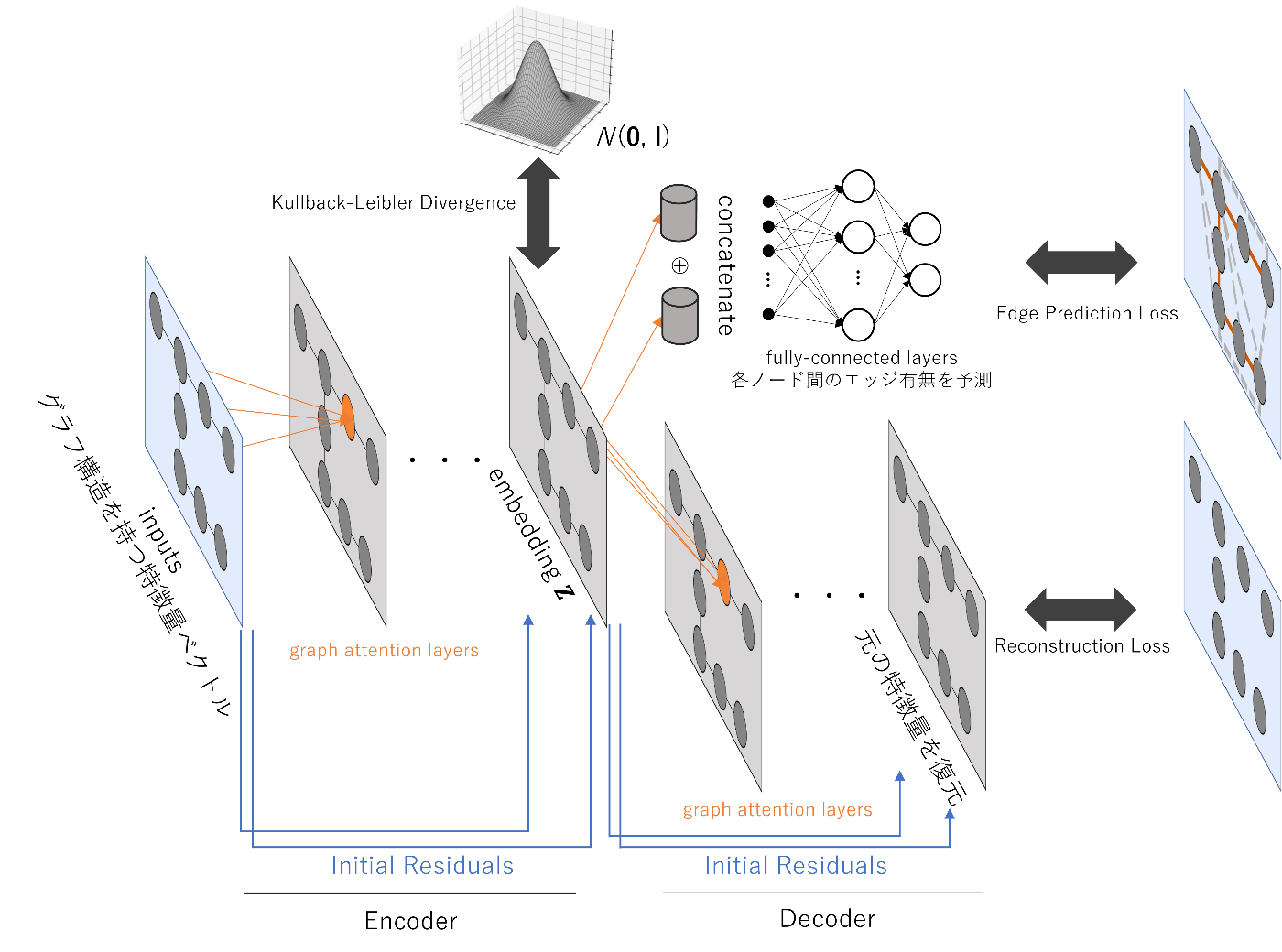
本記事で用いたモデルアーキテクチャ

まず、前項のグラフ構造を持つ特徴量ベクトルを用意し、Encoderによって、各ノードが持つ生データである特徴量ベクトルを潜在変数 \bm{Z} に埋め込みます（図中央のembedding \bm{Z}）。その \bm{Z} をDecoderによって元の生データ特徴ベクトルに復元する出力と、各ノード間のエッジ有無を予測する2種類[11]の出力を行います。このFeed Forwardの計算には、入力特徴量そのものに線形層をかませた特徴ベクトルを各層に加えています (図中青色矢印のInitial Residuals)。これによってoversmoothing problem (過剰平滑化問題) を避けています。今回は次数が非常に高いノードは存在しないので、neighbor explosion (近傍爆発) は問題になりません。

モデルの2種類の出力において、それぞれReconstruction Loss (再構成誤差を二乗誤差で定義)と、Edge Prediction Loss (交差エントロピー誤差で定義)を算出します。また、\bm{Z} を標準正規分布 N(\bm{0}, \bm{I}) に近づけるために、N(\bm{0}, \bm{I}) との Kullback–Leibler Divergence を計算し、この3つの合計を損失関数として、モデルを教師なし学習させます。
ただし、\bm{I} は単位行列であり、分散1、共分散0の分散共分散行列を表します。

EncoderもDecoderも、それぞれ4層のGATConvによって構成されています。グラフ畳み込みの方法としては、

  • GCN
  • GraphSAGE
  • Graph Attention Network (GAT)

などが候補に上がりますが、筆者の実験によって損失関数が最も良かったGATを採用しました。いずれの畳み込みも、本質的には近接ノードの情報を集約することに変わりはありません。

利用データ

対象駅

「関西のXX駅は関東のYY駅」を実現するには、関西と関東それぞれ1社以上の鉄道事業者を選定する必要があります。本記事では以下の2社にしました。

実は、阪急電鉄（以後「阪急」と書きます）と東急電鉄（以後「東急」と書きます）は似ているという声が少なからずあるようなので、似ている駅が見つかりやすいかもしれないというのが安直な選定理由です。
例えば東急電鉄様の公式X(旧Twitter)では以下のような言及がありました。

https://twitter.com/tokyugroup/status/1029252283144368128

東急電鉄では横浜線が2023年3月から開業していますが、オープンデータの方がまだ対応していないため、今回は横浜線を除外しました。また、東急世田谷線についても、オープンデータの仕様の都合で対象外とさせていただきました。ご了承ください。

特徴量とするデータの収集

以下のホームページからデータをダウンロードし、筆者により加工して利用しました（データは全て2023年8月30日取得）。

利用特徴量

今回モデルに付与したノード特徴量は以下の通りです[12]。

特徴量名 定義
公示地価 国土数値情報（地価公示データ）より、該当駅が最寄り駅になっている箇所の平均地価
次数 路線図を見たときに隣にある駅の数
平日昼人口 「全国の人流オープンデータ」（国土交通省）より、駅を含むメッシュ区間内の平日昼人口
休日昼人口 「全国の人流オープンデータ」（国土交通省）より、駅を含むメッシュ区間内の休日昼人口
平日深夜人口 「全国の人流オープンデータ」（国土交通省）より、駅を含むメッシュ区間内の平日深夜人口
休日深夜人口 「全国の人流オープンデータ」（国土交通省）より、駅を含むメッシュ区間内の休日深夜人口
平日昼夜人口比 平日昼人口 / 平日深夜人口
平日休日昼人口比 平日昼人口 / 休日昼人口
急行列車が止まるかどうか その駅に急行列車が停車するかどうか (停まるなら1, 停まらないなら0)

また、エッジ特徴量は以下の通りです。

特徴量名 定義
駅間距離 「駅データ」（駅データ.jp）の緯度経度のユークリッド距離
駅間hop数 路線図を見た時に、駅間の間にある駅の数+1 (隣接している場合1で、1駅間にあると2)

「急行列車が止まるかどうか」を除く全ての特徴量は、各鉄道事業者ごとに、

x \leftarrow (x - \mu) / \sigma

で標準化しています（ \mu はその特徴量の平均値、\sigma は標準偏差を表します）。関西と関東では絶対的な地価や昼人口などが違うため、鉄道事業者間でスケールを揃えるのがこの標準化の狙いです。

実験

実装

今回は Pytorch Geometric を用いて実装しました。Pytorch Geometric は Pytorch をバックエンドにしたライブラリで、GNNs の実装を簡単にしてくれます。
本節では、一部、キーとなるコードを抜粋して紹介します。全コードは以下の GitHub で公開しております。

https://github.com/atsushi-green/station2vec

VAEのEncoder

実装は以下の通りです。各グラフ畳み込み層のベクトル長を hidden_channels_list で用意しています。また、Initial Residual を実現するための線形層の重み行列も nn.Linear で定義し、forward メソッドで、各層に足す処理を加えています。

class VariationalGraohAutoEncoder(torch.nn.Module):
    def __init__(
        self,
        in_channels: int,
        hidden_channels_list: List[int],
        out_channels: int,
        edge_attr: torch.Tensor,
        dropout_rate: Optional[float] = 0.25,
    ):
        super().__init__()
        self.dropout = nn.Dropout(dropout_rate)
        self.edge_attr = edge_attr
        self.conv1 = GATConv(in_channels, hidden_channels_list[0])
        self.conv_list = [
            GATConv(hidden_channels_list[i], hidden_channels_list[i + 1]) for i in range(len(hidden_channels_list) - 1)
        ]
        # initial residualするための形揃えるための線形層
        self.initial_residual_list = [
            nn.Linear(in_channels, hidden_channels_list[i]) for i in range(1, len(hidden_channels_list))
        ]

        self.conv_mu = GATConv(hidden_channels_list[-1], out_channels)
        self.conv_logstd = GATConv(hidden_channels_list[-1], out_channels)

    def forward(self, x: torch.Tensor, edge_index: torch.Tensor) -> Tuple[torch.Tensor, torch.Tensor]:
        h = self.conv1(x, edge_index).relu()
        for conv, res in zip(self.conv_list, self.initial_residual_list):
            # graph conv
            h = conv(h, edge_index, edge_attr=self.edge_attr).relu()
            # initial residual
            x_ = res(x)
            h = h + x_
        return self.conv_mu(h, edge_index, edge_attr=self.edge_attr), self.conv_logstd(
            h, edge_index, edge_attr=self.edge_attr
        )

VAEのDecoder

Decoderの実装も、Encoderとほとんど同じです。こちらは2種類の出力が必要なので、2つのforwardメソッドを定義しています。forward メソッドでは入力を再現する予測をしていますが、0または1の値を取る特徴量 (今回で言うと急行が停まるかどうか) に対してはシグモイド関数を活性化関数として利用しています。edge_pred_forward メソッドでは、2つのノードの埋め込みベクトルをconcatしたものを入力特徴量として、Fully-connected Layerとシグモイド関数でエッジの有無を予測しています[13]。

class VariationalGraohAutoDecoder(torch.nn.Module):
    def __init__(
        self,
        embedding_channels: int,
        hidden_channels_list: List[int],
        out_channels: int,
        edge_attr: torch.Tensor,
        dropout_rate: Optional[float] = 0.25,
    ):
        super().__init__()
        self.dropout = nn.Dropout(dropout_rate)
        self.edge_attr = edge_attr
        self.sigmoid = nn.Sigmoid()
        # 自己符号化器としてのデコーダー
        self.conv1 = GATConv(embedding_channels, hidden_channels_list[0])
        self.conv_list = [
            GATConv(hidden_channels_list[i], hidden_channels_list[i + 1]) for i in range(len(hidden_channels_list) - 1)
        ]
        # initial residualするための形揃えるための線形層
        self.initial_residual_list = [
            nn.Linear(embedding_channels, hidden_channels)
            for hidden_channels in (hidden_channels_list[1:] + [out_channels])
        ]
        self.conv_final = GATConv(hidden_channels_list[-1], out_channels)

        # エッジ予測としてのデコーダー
        # エッジ予測に InnerProductDecoder を使うと、ベクトルが似たノード同士でエッジができやすくなるので、
        # エッジ予測はニューラルネットワークで行う。
        first_layer = nn.Linear(embedding_channels * 2, hidden_channels_list[0])  # 2つのノードの埋め込みをconcatしている
        mid_layer = [
            nn.Linear(hidden_channels_list[i], hidden_channels_list[i + 1])
            for i in range(len(hidden_channels_list) - 1)
        ]
        self.edge_predict_linear = [first_layer] + mid_layer
        self.edge_predict_final = nn.Linear(hidden_channels_list[-1], 1)

    def forward(self, z: torch.Tensor, edge_index: torch.Tensor) -> torch.Tensor:
        # 自己符号化器としてのデコーダー
        h = self.conv1(z, edge_index).relu()
        for conv, res in zip(self.conv_list, self.initial_residual_list):
            # graph conv
            h = conv(h, edge_index, edge_attr=self.edge_attr).relu()
            h = self.dropout(h)
            # initial residual
            z_ = res(z)
            h = h + z_

        h = self.conv_final(h, edge_index)
        z_ = self.initial_residual_list[-1](z)
        h = h + z_
        # 0-1をとる変数にはシグモイド関数をかませる
        h[:, CROSS_ENTROPY_INDEXES] = self.sigmoid(h[:, CROSS_ENTROPY_INDEXES])
        return h

    def edge_pred_forward(self, z1: torch.Tensor, z2: torch.Tensor) -> torch.Tensor:
        """z1の埋め込みを持つノードと、z2の埋め込みを持つノードの間にエッジがある確率を返す。

        Args:
            z1 (torch.Tensor): 埋め込みベクトル
            z2 (torch.Tensor): 埋め込みベクトル

        Returns:
            torch.Tensor: エッジの有無を表す確率
        """
        # エッジ予測としてのデコーダー
        h = torch.cat([z1, z2], dim=1)
        for linear in self.edge_predict_linear:
            h = linear(h).relu()
            h = self.dropout(h)
        h = self.edge_predict_final(h)
        return self.sigmoid(h)

モデルの学習

ハイパーパラメータは以下の通りです。本来であればバリデーション誤差を見て学習を止めるべきですが、今回は10,000回学習させたところで止めてしまいます。

ハイパーパラメータ 値
エポック数 10,000[14]
埋め込みベクトルの次元数 5
EncoderのGATConvの隠れ層の次元数 20, 20, 15, 10, 5(埋め込みベクトル)
DecoderのGATConvの隠れ層の次元数 5(埋め込みベクトル), 10, 15, 20, 20
DecoderのFully-connected Layerの隠れ層の次元数 10(埋め込みベクトル×2), 20, 20, 15, 10, 2
学習率の初期値 0.01
最適化手法 Adam

実行結果 (の一例) は以下の通りで、誤差は収束していそうです。

epoch:100, loss:8.1399
epoch:200, loss:7.6064
epoch:300, loss:7.2345
epoch:400, loss:6.8291
epoch:500, loss:6.2023
epoch:600, loss:5.9493
epoch:700, loss:5.6712
（中略）
epoch:9200, loss:4.0945
epoch:9300, loss:4.0336
epoch:9400, loss:3.9880
epoch:9500, loss:5.4786
epoch:9600, loss:4.5077
epoch:9700, loss:4.3908
epoch:9800, loss:4.3518
epoch:9900, loss:4.1444
epoch:10000, loss:4.1048
100%|█████████████████████| 10000/10000 [02:35<00:00, 64.22it/s]

今回は商用利用可能なオープンデータのみを利用していますが、データセット作成の手順を残していないので[15]、そのままでは学習することはできない点をご了承ください。今回利用したデータは量は非常に少ないので、GPUを使わずにCPUだけで学習しても2分半程度で学習が終わりました。

対抗馬の設定

GNNを用いたことによるメリットを評価するために、GNNを用いない方法で1つ、実験してみました。鉄道事業者ごとのデータの標準化をして、PCAでGNNを用いた方法と同じ5次元に圧縮して、各駅の埋め込み表現を決めました。

結果と感想

ある2駅の似ている度合いはcos類似度[16]を用いることで定量的に測ることができますが、似ているかどうかは定性的な判断しかできません。「前提」の節でも書いた通り、当たっていたり当たっていなかったりしながら楽しみましょう。

なお、似ている駅は、cos類似度が1に近い駅、似ていない駅はcos類似度が-1に近い駅として選出しています。なお、cos類似度が0の駅とはどんな駅かは、解釈が難しかったので本記事では対象外とします。

主要な駅の結果を以下の表にまとめました。なお、筆者の気まぐれでGitHub Pagesで公開している方のモデルをアップデートする可能性があるので、本記事で書かれた結果が異なる場合がございます。ご了承ください。

横浜駅(東急)と似ている駅・似ていない駅

まずは本記事のタイトルにも出している、横浜駅を見てみます。似ている駅として、神戸三宮駅が GNNでは4位、PCAでは1位として選出され、なんとか無事、タイトルを回収できました[17]。また、他に似ている駅はいずれも都心部となっていいるのと、似ていない駅は住宅街が中心に挙がっていることから、VAEの再構成誤差が効いてくれていて、納得の結果です。

順位 GNN似ている駅 GNN似ていない駅 PCA似ている駅 PCA似ていない駅
1位 烏丸(阪急) つきみ野(東急) 神戸三宮(阪急) 緑が丘(東急)
2位 京都河原町(阪急) すずかけ台(東急) 大阪梅田(阪急) 田奈(東急)
3位 大阪梅田(阪急) こどもの国(東急) 中目黒(東急) 大倉山(東急)
4位 神戸三宮(阪急) 恩田(東急) 大井町(東急) つくし野(東急)
5位 蒲田(東急) つくし野(東急) 京都河原町(阪急) つきみ野(東急)

江田駅(東急)と似ている駅・似ていない駅

次は横浜とは毛色の異なる駅として、東急の閑静な住宅街の1つである江田駅[18]を見てみます。GNNでの似ている駅、1位:あざみ野駅、3位:市が尾駅は、江田駅と路線図上で隣り合っています。一方、PCAの方では、地理的に近い駅が挙がっていません。これは、GNNが隣接ノードの情報を集約していること、エッジの有無の予測を行っていることによって、隣接ノードの情報を利用していることを示唆しています。

順位 GNN似ている駅 GNN似ていない駅 PCA似ている駅 PCA似ていない駅
1位 あざみ野(東急) 神戸三宮(阪急) 松尾大社(阪急) 三軒茶屋(東急)
2位 宝塚南口(阪急) 京都河原町(阪急) 妙蓮寺(東急) 烏丸(阪急)
3位 市が尾(東急) 烏丸(阪急) 山田(阪急) 神戸三宮(阪急)
4位 売布神社(阪急) 目黒(東急) 苦楽園口(阪急) 西院(阪急)
5位 大山崎(阪急) 五反田(東急) 九品仏(東急) 武蔵小杉(東急)

渋谷(東急)と似ている駅・似ていない駅

今度は日本を代表する都心駅、東急渋谷駅を確認してみます。GNNもPCAも、およそ似ている駅は都心駅で、似ていない駅には落ち着いた駅が上位にランクインしていますね。繁華街でもない代官山がGNN、PCAともにランクインしているのは意外な結果ですが、これは人口に関するcos類似度を計算しているので、昼夜・平日休日の人口比率が似ていれば(同じベクトルを向いていれば)、似ている駅としてランクインしてしまいます。

順位 GNN似ている駅 GNN似ていない駅 PCA似ている駅 PCA似ていない駅
1位 大阪梅田(阪急) 松尾大社(阪急) 大阪梅田(阪急) 白楽(東急)
2位 代官山(東急) 東向日(阪急) 代官山(東急) 宮前平(東急)
3位 五反田(東急) 南町田グランベリーパーク(東急) 横浜(東急) 洗足池(東急)
4位 大崎広小路(東急) つきみ野(東急) 五反田(東急) 東白楽(東急)
5位 横浜(東急) 西向日(阪急) 目黒(東急) 石川台(東急)

大阪梅田駅(阪急)と似ている駅・似ていない駅

ここからは阪急の駅を見てみましょう。まずは阪急で最も規模の大きい駅、大阪梅田です。やはり似ている駅には都心駅が上位にランクインしています。こちらも渋谷駅の時と同様、代官山がランクインしていますが、同様の理由と考えられます。

順位 GNN似ている駅 GNN似ていない駅 PCA似ている駅 PCA似ていない駅
1位 渋谷(東急) つきみ野(東急) 渋谷(東急) 妙蓮寺(東急)
2位 烏丸(阪急) 嵐山(阪急) 横浜(東急) 鵜の木(東急)
3位 京都河原町(阪急) すずかけ台(東急) 代官山(東急) 白楽(東急)
4位 横浜(東急) こどもの国(東急) 神戸三宮(阪急) 緑が丘(東急)
5位 代官山(東急) 中央林間(東急) 中目黒(東急) 洗足池(東急)

池田駅(阪急)と似ている駅・似ていない駅

最後に、飲食店も多く、住宅街とも言われている池田駅を見てみます。これはGNNの効果が顕著に出ているように見えます。GNNの似ている駅で上位にランクインしている川西能勢口駅、石橋阪大前駅、桜井駅は、以下の阪急路線図の抜粋の通り、池田駅の近くにあります。これはまさに、GNNによる隣接ノードの畳み込み・エッジ予測の影響と考えられます（PCAの方にはこの傾向は見られないです）。

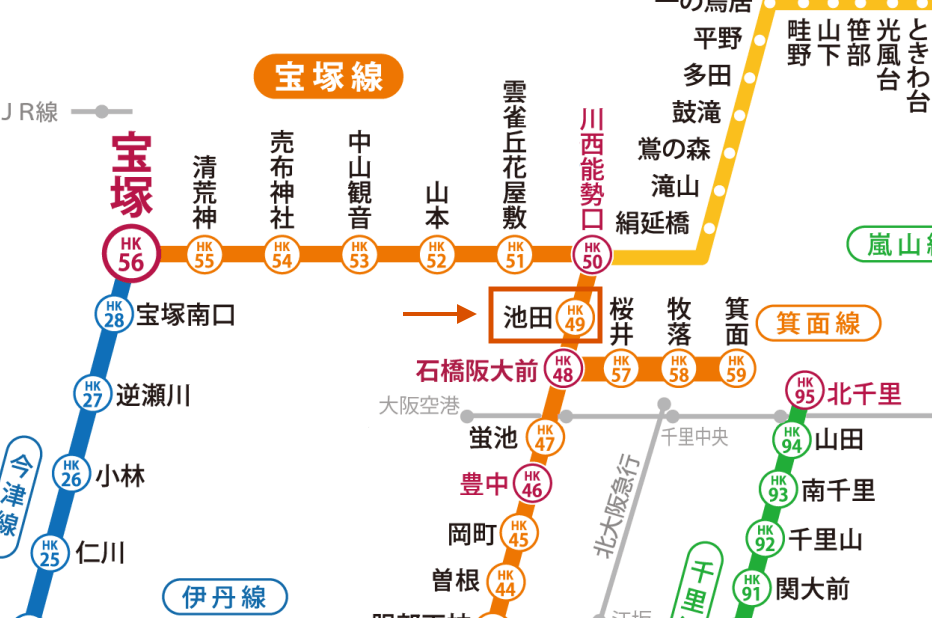
ikeda
阪急池田駅周辺の路線図 (https://www.hankyu.co.jp/station/pdf/map_station.pdf より引用。一部加工。)

順位 GNN似ている駅 GNN似ていない駅 PCA似ている駅 PCA似ていない駅
1位 川西能勢口(阪急) 神戸三宮(阪急) 春日野道(阪急) 都立大学(東急)
2位 石橋阪大前(阪急) 京都河原町(阪急) 西京極(阪急) 用賀(東急)
3位 桜井(阪急) 烏丸(阪急) 六甲(阪急) 稲野(阪急)
4位 上牧(阪急) 五反田(東急) 南茨木(阪急) 桜新町(東急)
5位 西山天王山(阪急) 大崎広小路(東急) 菊名(東急) 祐天寺(東急)

結び

本記事では、鉄道路線図に対してGNNsとVAEを適用し、駅の埋め込み表現を学習させました。GNNsを用いたことで、隣接している駅同士の似ている度合いを高められたことを一部確認できました。

実は今更ですが現状、鉄道路線図に対してGNNsを用いるのはあまり良い方法ではないと考えています。実際、鉄道路線図に対してGNNsを適用している事例は少ないです。というのも、GNNsではエッジで結ばれているノード同士には関係性が強いことを仮定しているにも関わらず、路線図において駅同士が隣り合っているということが、ノード同士(駅同士)に関連性があるとは限らないからです。逆に、隣り合っていない駅同士が似ているということは非常によくあります。隣り合っていれば確かに地理的な位置関係という意味で似ているかもしれませんが、今回扱ったような昼夜人口などの駅の性質は大きく異なることがあるでしょう。また、他のエッジの繋ぎ方のアイデアとして人流の多さ (よく言われるODデータ[19])でエッジを定義する方法もあり得たかもしれませんが、A駅からB駅に移動する人が多いからといって、A駅とB駅が似ているとは限らないので、こちらもあまり良い方法ではなさそうです。

こういう訳で、今回GNNsを用いた利点は「非都心駅において、地理的に近しい駅同士を似ているとする」程度の効果しかありませんでした。反省文のような結びになってしまいましたが、将来的には路線図というグラフ構造から、効果的な特徴量抽出ができるような新たなGNNsの研究が進むことを期待すると同時に、それに貢献していきたいと考えています。

参考文献

お知らせ

少しでも弊社にご興味を持っていただけた方は、お気軽にご連絡頂けますと幸いです。まずはカジュアルにお話を、という形でも、副業を検討したいという形でも歓迎しています。

https://recruit.zenkigen.co.jp/career
https://speakerdeck.com/zenkigenforrecruit/detailed-version-recruitment-materials-for-data-scientists

脚注

  1. xx2yy という表記で、xxをyyに変換するという意味でよく使われています。2は英語の to から来ています。 ↩︎

  2. 単語などの定性的な概念、シンボルを多次元の実数ベクトルで表現することです。 ↩︎

  3. 技術者たるもの、好きな技術は何かと聞かれれば即答しちゃうものですよね。私の場合はGNNsです。 ↩︎

  4. 「関東のXX駅は関西のYY駅」を実現するためには、個人的には飲食店の種類や多さ、近くにある商業施設の規模のような、周辺施設の情報を与えるのがもっともらしくなると思っていますが、考え出すとキリがないので、今回は割り切ったデータになっています。 ↩︎

  5. 路線図以外のグラフでは、これだけ離れていればノード間に関係性がないと捉えて無視できるかもしれません。しかし路線図の場合、中央林間(東急路線図の左上端にある駅)から渋谷駅(東急路線図の右上端にある駅)など、長距離の移動も考えられるため、ある程度遠いノードの関係性も加味する必要があるかもしれません。 ↩︎

  6. あるノードに隣接しているノードの数のことです。 ↩︎

  7. ノードが熱源で、それがGCN層を通るたびに隣ノードへ広がっていく、というのを各ノードが繰り返していると、グラフ全体が似たような温度になる、というようなイメージを筆者は持っています。 ↩︎

  8. 何個隣のエッジであるかを区別するための工夫はしております。詳細は利用特徴量の節をご覧ください。 ↩︎

  9. 20個程度では、路線図を全て網羅しきれませんが20個もあればおよそ最寄りの都心駅にいけるはずと信じています。 ↩︎

  10. 各ノードが、自分自身へのノードとつながるエッジを意味します。 ↩︎

  11. Variational Graph Auto-Encoders の論文では、単にエッジの有無を予測するように紹介されていますが、ノード特徴量を再現するのに必要な情報を潜在変数 \bm{Z} に反映させたいので、2種類の出力を出すようにしました。 ↩︎

  12. 人口に関するデータは、2022年9月現在利用可能なデータが2021年まででした。今回は最新かつ長期休暇などの影響を受けにくい2021年11月のデータを利用しました。 ↩︎

  13. Variational Graph Auto-Encoders の論文では、2つの潜在変数の内積にシグモイド関数で活性化させることでエッジの有無を予測しています。これは、2つのノード埋め込み表現が似ているならばエッジは存在するということを意味しているので、今回の駅の埋め込み表現学習には適していません。そこで、普通の Fully-connected Layer によってエッジの有無を予測するように変更しています。 ↩︎

  14. グラフが大きいときは、ノードをサンプリングして、それをミニバッチとして学習させるのことが一般的です。ただし、今回はグラフが小さいので、グラフ全体を1イテレーションで一気に学習させています。すなはち、1イテレーション = 1エポック ということになります。 ↩︎

  15. すいません、シンプルに面倒でした。前処理のソースコードと、データへのリンクは載せてあリます。どうしても手元で再現したい方はX(旧Twitter)にて直接お声がけください。 ↩︎

  16. ベクトル \bm{x}=(x_1, \cdots, x_n)^T, \bm{y} = (y_1, \cdots, y_n)^T のcos類似度は cos(x,y)=\frac{<\bm{x},\bm{y}>}{||\bm{x}|| \cdot \bm{||y||}} で与えられる。ただし、\bm{||\cdot||} はノルムを表し、<>は内積を表す。cosの性質(というより定義)から、-1~1の値を取るため扱いやすいです。 ↩︎

  17. 横浜と神戸は、港町であったり、中華街があったり、都心であったり、共通点が多くて似ているという印象を持つ方が多いと思います。本記事では、昼夜人口、地価、路線図に関する情報しか与えていないため、この結果が得られたのは(都心であるということを除いては)あくまでも偶然です。 ↩︎

  18. 路線図から田園都市線(緑の線)の中央左寄りを探してみてください。急行が停まらない駅です。 ↩︎

  19. Origin-Destination の略。どこからどこへ移動したかの情報という意味です。 ↩︎

ZENKIGENテックブログ
ZENKIGENテックブログPublication

私たちは「はたらく人の理想」をつくるために、ITと科学で組織課題に立ち向かうAIテックカンパニーです。「テクノロジーを通じて人と企業が全機現できる社会の創出に貢献する」のVisionのもと、人の感覚に寄り添うテクノロジーを用いたでサービスを展開しています。

Discussion