グラフニューラルネットワーク(GNN)徹底解説！用途と仕組みからPyGでの実装まで

株式会社ディー・エヌ・エーに AI スペシャリストとして新卒で入社した @634kami です。

CNNなどディープなニューラルネットワークの台頭により一躍世界中の関心を集めるようになった機械学習分野ですが、最近の生成AIブームによりますます関心が高まっています。機械学習については、画像や自然言語といった馴染み深いデータを対象に扱うものについてはよく知られていますが、グラフと呼ばれるデータを扱うグラフニューラルネットワーク(GNN) については研究における注目度の割に、世間からの知名度がありません。

この記事では、グラフについて知らない方でも分かるように、最初にGNNが何に使えるのかの話を中心に解説した後、実際の仕組みを知りたい方向けにモデルの紹介や様々なトピックについて網羅的に解説します！また、最後に PyTorch Geometric(PyG) を利用した実装方法についても触れます。

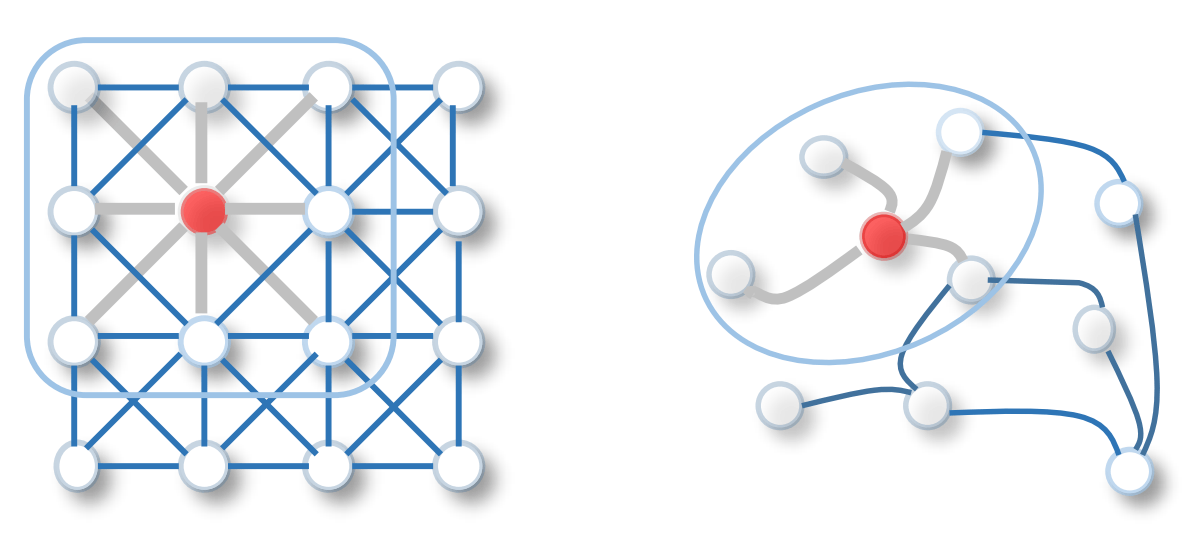
(画像引用元：Wu, Z., Pan, S., Chen, F., Long, G., Zhang, C. and Philip, S.Y., 2020, Fig. 1 ^[1])

前提知識・背景

まずはグラフについてご存知無い方向けに、前提知識や何に使えるのかの背景について説明します。

ここで言うグラフは、通常世間一般で用いられる「（関数やデータを視覚化した）グラフ」ではなく、離散数学におけるグラフを指しているので注意してください。

(離散数学における)グラフとは

グラフは、頂点(ノード)と、頂点同士の関係を表したデータ構造です。

主に以下の2つから構成され、$G=\{V, E\}$などと表現されることが多いです。

• 頂点(ノード): $V$
• 辺(エッジ/リンク): $E(\subset V \times V)$
  • エッジはどちらの頂点を始点としてどちらの頂点を終点とするのかの方向性を持つことがあり、このようなグラフを「有向グラフ」と呼びます
  • 逆に向きを持たないグラフを「無向グラフ」などと呼びます

具体例で見てみましょう。下の図は、頂点の集合が $V=\{0,1,2,3\}$ 、辺の集合が $E=\{(0,1),(0,2),(2,1),(2,3)\}$ となるグラフを表した図です。

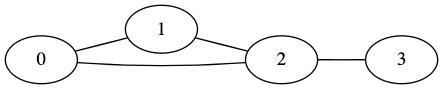
このように表すと何に役立つのか分かりにくいですが、物同士の関係性を直感的に表すことができるため、日常の様々なところでこのグラフ構造が現れます。
具体的にどのような時にグラフ構造が現れるのかを確認してみましょう。

グラフの例

ソーシャルネットワーク

SNSでのフォロー関係などをエッジとしてみなすとグラフ構造となります。このようなある種の社会的相互作用によって生まれるようなネットワークをソーシャルネットワークと呼ぶことがあります。

社会学・社会心理学などの学問とグラフ理論などの側面が合わさった学際的な分野として、ソーシャルネットワークを始めとしたネットワーク構造を分析するネットワーク科学と呼ばれる分野もあります。

このようなネットワーク構造にはグラフの様々な理論が適用できるため応用上でも有用です。

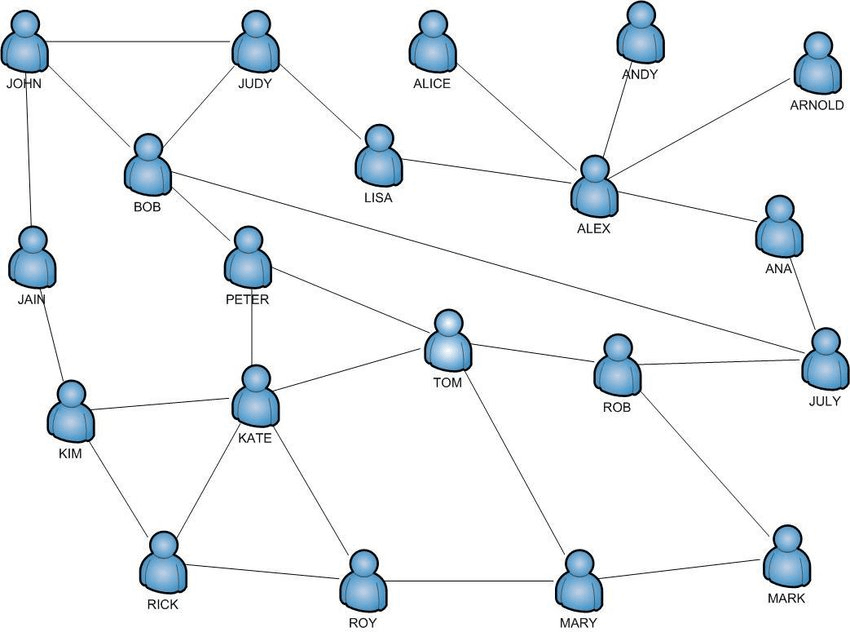
(画像引用元：Filipowski, T., Kazienko, P., Brodka, P. and Kajdanowicz, T., 2012, Figure 2 ^[2])

道路ネットワーク
交差点をノード・道路をエッジとしてみなしたものは道路ネットワークなどと呼ばれることがあります。道路に限らず、駅をノード・線路をエッジとしたグラフなどを含めて交通ネットワークと呼ばれることもあります。

このようなグラフを考えることは応用上で様々な利点があります。

例えば、ある地点からある地点までの最短経路を求めたいときは、このグラフ上でのアルゴリズムを考えることになります。また、GPSから得られる情報を道路ネットワーク上の情報と照らし合わせて自然な経路になるように修正することなども取り組まれています。

(画像引用元：Hu, Z., Shao, F. and Sun, R., 2022, Figure 1 ^[3])

他にもグラフには様々な例がありますが、GNNの応用例について述べる際に追加で言及します。

グラフニューラルネットワーク(GNN)とは

グラフニューラルネットワークとは、グラフデータをニューラルネットワークで扱うものの総称です。近年非常に注目されている分野で、関連論文が増えています。

まずは数式が苦手な方でも分かりやすいように、何のために使われているのかや、どんな応用例があるのかについて確認しましょう。

その後、モデルについての詳細な説明をしていきます。様々なモデルが提案されているため、なるべく一般的・統一的な説明をした後に、必要に応じて細かなモデルについても説明します。

(画像引用元：Wu, Z., Pan, S., Chen, F., Long, G., Zhang, C. and Philip, S.Y., 2020, Fig. 1 ^[1:1])

GNN で解きたいタスク

グラフが色々なところで現れるという説明はしましたが、GNNで実際何ができるのでしょうか？

GNNでやりたいことは大きく分けると3種類あり、「頂点(ノード)」「辺(エッジ/リンク)」「グラフ全体」に関するタスクがあります。

以下はそれぞれのタスクにおける代表的なものです。

• 頂点(ノード)
  • クラス分類・回帰
  • クラスタリング
    • 頂点をいくつかのグループに分割する
• 辺(エッジ/リンク)
  • link prediction
    • ある頂点間に辺があるかどうかを予測する
  • クラス分類・回帰
• グラフ全体
  • クラス分類・回帰
  • グラフオートエンコーダー(GAE)
    • グラフをベクトルにエンコードするエンコーダーと、ベクトルから元に再構成するデコーダーを学習する

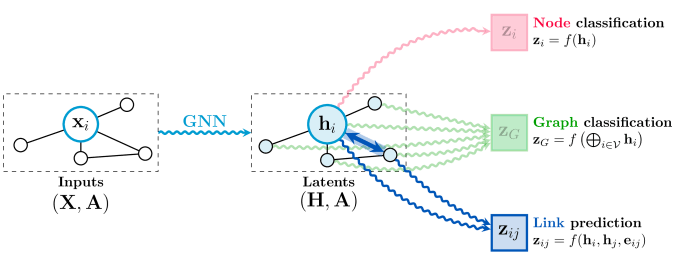
(画像引用元：Veličković, P., 2023, Figure 1 ^[4])

これだけ見ても抽象的で分かりにくいかも知れません。具体的にどのような場面で使われるのかについて見ていきましょう。

GNNの応用例

GNNの応用例としては様々なものがあります。

Graph Miningと呼ばれる分野ではグラフ上でのマッチングが研究されていたり、物理学でも物理システムのモデリングに利用されていたりします。また、タンパク質間の相互関係をグラフとして見てGNNを適用する事例あるなど、様々な分野で利用されています。

先程説明したソーシャルネットワーク上では、友達関係があるかどうかの予測(link prediction)を行うこともあります。

(画像引用元：Zhou, J., Cui, G., Hu, S., Zhang, Z., Yang, C., Liu, Z., Wang, L., Li, C. and Sun, M., 2020, Fig. 6 ^[5])

さらなる詳細な例として、化学反応の予測とレコメンドシステムを確認しましょう。

化学反応の予測
化学反応などの関係を考える際にもグラフ構造が用いられることがあります。

頂点を分子・化学反応を辺として扱うことでグラフ構造とみなす事が可能です。このグラフに対してGNNを用いることで反応の成功を予測することができます。

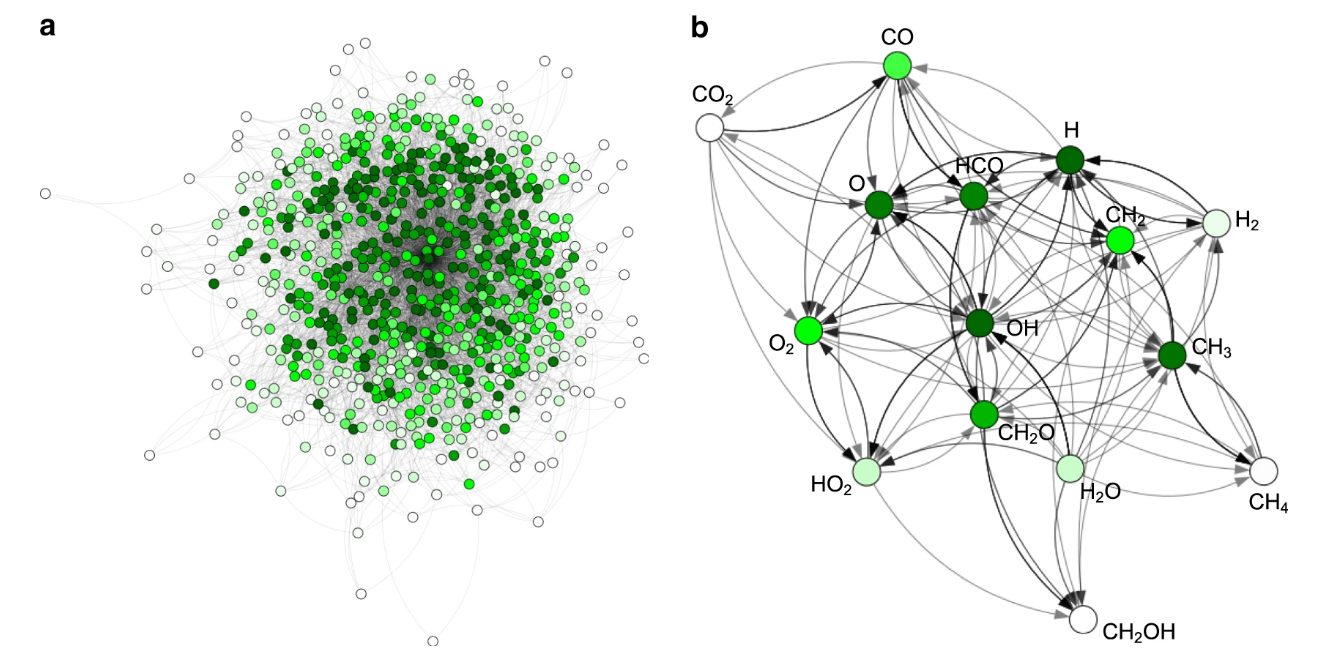
(画像引用元：Stocker, S., Csányi, G., Reuter, K. and Margraf, J.T., 2020, Fig. 1 ^[6])

レコメンドシステム
レコメンドの文脈においてもGNNが近年良く使われるようになっています。

何かしらのシステム上において、ユーザーとアイテムの関係性（クリックしたか・購入したか・お気に入り登録したか等）をグラフの辺としてみなすことができる場合というのは非常に多いです。

このようなシステムで、ユーザー体験を向上させたり、売上を上げたりするために、ユーザーに対して最適なアイテムをレコメンドしたくなる場面は多くあります。

このグラフ構造に対してGNNを適用することで、従来の手法よりも性能の高いレコメンドシステムを構成することなどが研究されています。

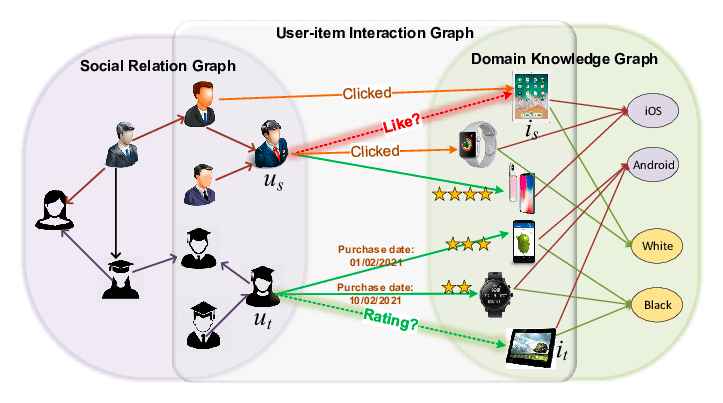
(画像引用元：Wang, S., Hu, L., Wang, Y., He, X., Sheng, Q.Z., Orgun, M.A., Cao, L., Ricci, F. and Yu, P.S., 2021, Figure 1 ^[7])

GNNの一般的な構成と代表的なモデル

GNNを利用するモチベーションについては確認できました。それでは具体的にどのような仕組みなのかを見ていきましょう。

多くのGNNでは、入力データとなるグラフをGNNの層に通し、出力として得られる 頂点/辺/グラフ の埋め込み表現をその後の学習や予測に用います。

以下はGNNの一般的な構成についての図です。

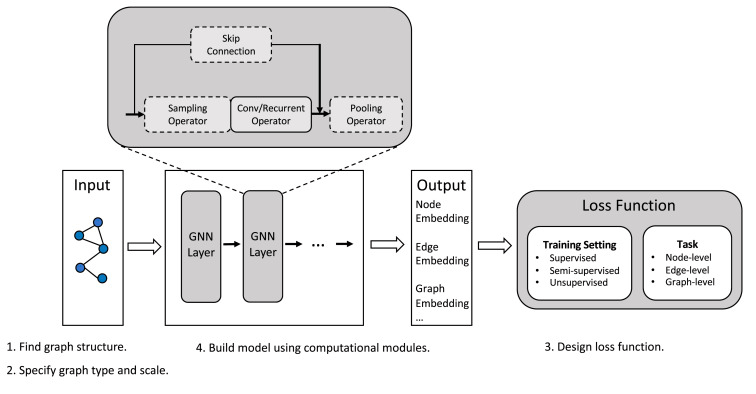
(画像引用元：Zhou, J., Cui, G., Hu, S., Zhang, Z., Yang, C., Liu, Z., Wang, L., Li, C. and Sun, M., 2020, Fig. 2 ^[5:1])

入力として与えられたグラフに対して、「GNN Layer」を複数適用し、得られた埋め込み表現(Embedding)を用いて学習時に損失(loss)を計算したり、推論時に予測したりします。

この図の「GNN Layer」や「computational modules」周辺に相当する部分には様々なものが提案されています。以下は同じ論文中にあった「computational modules」を分類した図です。

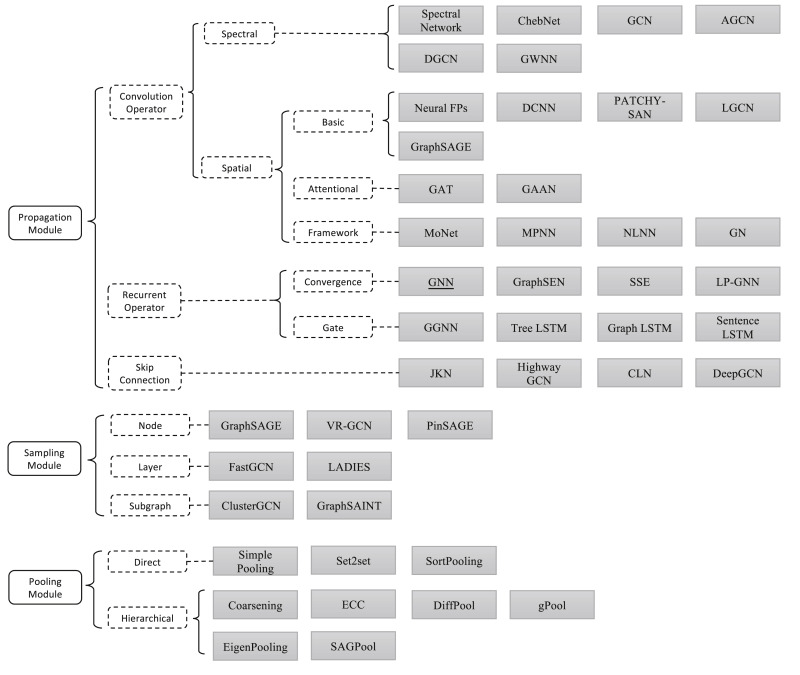
(画像引用元：Zhou, J., Cui, G., Hu, S., Zhang, Z., Yang, C., Liu, Z., Wang, L., Li, C. and Sun, M., 2020, Fig. 3 ^[5:2])

初期に論文が出た時点ではまだまだ体系化されておらず、後に出た論文で一般化され数式として整理されることが多いように感じます。そのため非常にとっつきにくくなっています。

この記事では、特に代表的なグラフ畳み込み演算（Graph Convolution Operator) に関する手法として、Spectral な手法 と Spatial な手法について体系的に解説します。
また、Spatial な手法の問題を解決するための方法として提案されている samping を用いたモデルについても解説します。

用語と定義について

モデルの説明のために、まずは基本的な単語の意味などをここでまとめて説明しておきます。

ここ以降はモデルの説明のために数式を用いる場合も多くなるため、必要なものはここで定義することにします。

表記	説明
$N$	グラフの頂点数
$M$	グラフの辺数
$\bm{A}$	$N \times N$ の隣接行列。$(i,j)$ 成分が 1 なら頂点 $i, j$ 間に辺があることを表し、0なら無いことを表す。
$\bm{I}$	$N \times N$ の単位行列
$\bm{D}$	$N \times N$ の次数行列。対角成分に対応する頂点の次数を持つ。
$\bm{L}$	ラプラシアン行列(定義は後述)。正規化された次のものが使われることが多い
$\bm{\~{A}}$	正規化隣接行列。$\bm{\~{A}}:=\bm{D}^{-1/2}\bm{A}\bm{D}^{-1/2}$
$\bm{\~{L}}$	正規化ラプラシアン行列(定義は後述)。性質が良いのでスペクトルグラフ理論の文脈でよく出てくる。固有値分解すると $\bm{\~{L}}=\bm{U}\bm{\Lambda}\bm{U}^T$ となる。
$\bm{U}$	$\bm{\~{L}}$ の固有ベクトルを並べた行列。
$\bm{\Lambda}$	$\bm{\~{L}}$ の固有値を対角要素に並べた行列
$D$	ここでは頂点ごとの特徴量の数
$\bm{X}$	頂点の特徴行列。$\bm{X} \in \mathbb{R}^{N \times D}$ となる。
$\bm{x}$	グラフシグナル。$\bm{x} \in \mathbb{R}^N$ となる。ベクトルの各要素が各頂点のスカラー値に対応する。また、特徴行列 $\bm{X}$ の列一つがグラフシグナルに対応する

ラプラシアン行列と正規化ラプラシアン行列

グラフデータを表現する方法としては隣接行列 $\bm{A}$ が有名ですが、スペクトルグラフ理論と呼ばれる分野ではラプラシアン行列と正規化ラプラシアン行列がよく出てきます。

これらは Spectral な GNN モデルを扱う際に頻出する表現なのでここで確認しておきましょう。

ラプラシアン行列

$$\bm{L}:=\bm{D}-\bm{A}$$

正規化ラプラシアン行列

$$\begin{aligned} \bm{\~{L}} &:= \bm{D}^{-1/2}\bm{L}\bm{D}^{-1/2}\\ &=\bm{I}-\bm{D}^{-1/2}\bm{A}\bm{D}^{-1/2} &=\bm{I}-\bm{\~{A}} \end{aligned}$$

Spectral な GNN モデル

それでは具体的な GNN のモデルとして Spectral なアプローチを用いたものをまず確認していきましょう。

これらのアプローチは理論的にはスペクトルグラフ理論(Spectral Graph Theory) に深く関わっているため、「Spectral」と呼ばれています。

特にグラフフーリエ変換と呼ばれるものと深い関わりがあるため、理解ができるように必要な知識から順を追って説明します。

前知識：グラフフーリエ変換（Graph Fourier Transform）

一般的なフーリエ変換をグラフ上でも適用できるようにしたものとして、グラフフーリエ変換があります。

フーリエ変換
この記事ではグラフニューラルネットワークの解説を目的としているので深く触れませんが、通常の信号 $f(t)$ に対するフーリエ変換を軽く確認しておきましょう。

フーリエ変換 $F(\xi)$ は以下の形式で定義されます。

$$F(\xi):= \langle f(t), \exp(-2\pi i t \xi) \rangle = \int_{-\infty}^{\infty}f(t) e^{-2\pi it \xi}dt$$

$t$ の関数 $f(t)$ から、$\xi$ の関数 $F(\xi)$ を作るような変換になります。

グラフフーリエ変換
上述した通常のフーリエ変換をグラフに対して拡張することで、グラフの頂点 $V$ 上のグラフ信号 $\bm{x} \in \mathbb{R}^N$ に対するグラフフーリエ変換(Graph Fourier Transform)を以下のように定義することができます。

$$F(i):= \langle \bm{x}, \bm{U}_{i} \rangle = \sum_{k=0}^{N-1} x(k) U_{i}(k)$$

ここで $x(k)$ は $\bm{x}$ の $k$ 要素目、$U_{i}(k)$ も $\bm{U}_{i}$ の $k$ 要素目を表します（$\bm{U}_{i}$ 自体は i 番目の固有ベクトルを表す）。

通常のフーリエ変換では、信号(シグナル) $f(t)$ と固有関数 $\exp(-2\pi i t \xi)$ の積の積分でした。グラフフーリエ変換では、グラフシグナル $\bm{x}$ と固有ベクトル $\bm{U}_{i}$ の積の和を考えることになります。

さて、上述の形式を行列でまとめるとグラフフーリエ変換は以下の形で表現できます。

$$F(\bm{x}) = \bm{U}^T \bm{x}$$

そして、逆グラフフーリエ変換は以下のように表現できます。

$$F^{-1}(\bm{x}) = \bm{U} \bm{x}$$

このあたりの詳細について知りたい方は [Shuman, D.I., Narang, S.K., Frossard, P., Ortega, A. and Vandergheynst, P., 2013]^[8] などを見ると良いでしょう。

Spectral Convolution

グラフフーリエ変換とスペクトル空間上のフィルター $\bm{U}^T\bm{g}$ を用いて、グラフスペクトルに対する畳み込み演算は以下のように定義されます。

$$\bm{g} \ast \bm{x} = F^{-1}(F(\bm{g}) \odot F(\bm{x})) = \bm{U}(\bm{U}^T\bm{g}\odot\bm{U}^T\bm{x})$$

ここで $\odot$ は要素ごとの積を表しています。

しかし、フィルターについては $\bm{U}^T\bm{g}$ のままでは扱いにくいので、シンプルなものとして学習可能な対角行列 $\bm{g}_w$ などが良く用いられています。

$$\bm{g}_w \ast \bm{x} = \bm{U} \bm{g}_w \bm{U}^T\bm{x}$$

まとめると以下のように畳み込みが行われます

1. グラフのシグナル $\bm{x}$ をグラフフーリエ変換によってスペクトル空間上に変換する
2. スペクトル空間上でフィルターをかける
3. もとの空間に戻すために、逆グラフフーリエ変換を行う

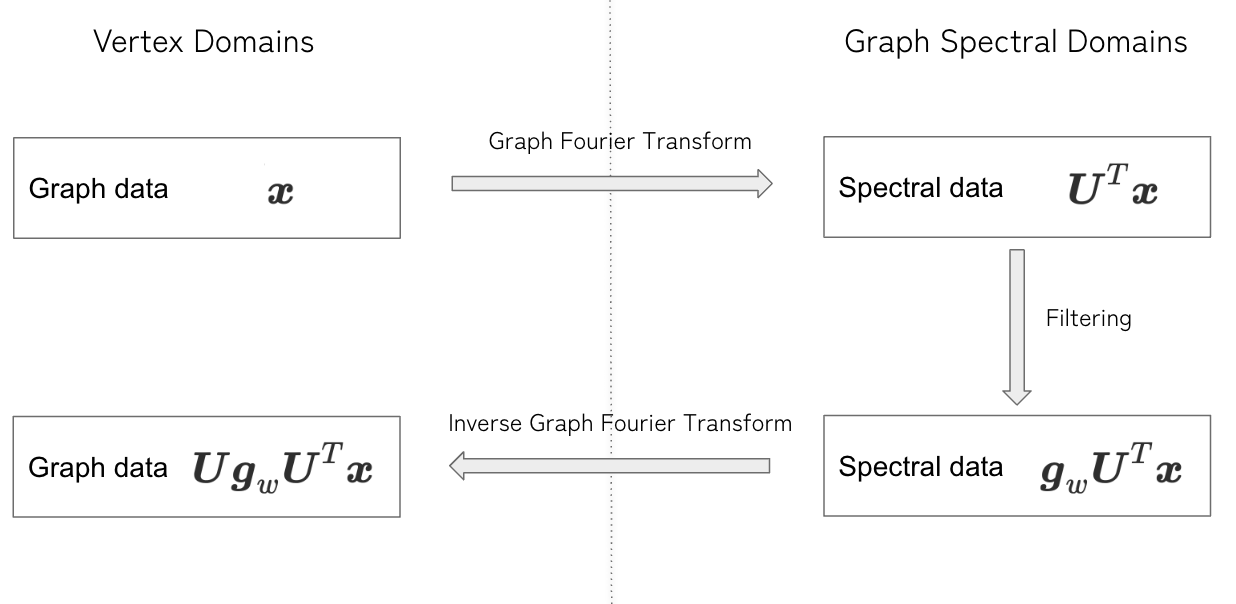
Spectral Graph Neural Network　の別の表現

具体的なモデルを確認するまえに、spectral convolution の表現方法についてもう一つ確認してみましょう。

いくつかのモデルについては、直接的に $\bm{g}_w \ast \bm{x} = \bm{U} \bm{g}_w \bm{U}^T\bm{x}$ の形をしていないのにも関わらず、Spectral GNN と呼ばれることがあります。

このようなモデルでは固有値を用いたフィルターを用いることがあり、 $\bm{g}_w := g(\bm{\Lambda})$ のように表現します。しかし、直接固有値分解を用いるのは計算量の課題があるため、以下のように次数Kの多項式として表現することでうまく変形することができます。

$$g(\bm{\Lambda}) = \sum_{k=0}^Kw_k (I-\bm{\Lambda})^k$$

すると畳み込みは以下のように変形できます。

$$\begin{aligned} \bm{U}g(\bm{\Lambda})\bm{U}^T\bf{X} & = \bm{U}(\sum_{k=0}^Kw_k (I-\bm{\Lambda})^k)\bm{U}^T\bm{X} \\ & = \sum_{k=0}^Kw_k \bm{U}(I-\bm{\Lambda})^k\bm{U}^T\bm{X}\\ & = \sum_{k=0}^K w_k (I-\bm{U}\bm{\Lambda}\bm{U}^T)^k \bm{X}\\ & = \sum_{k=0}^K w_k {\~{\bm{A}}}^k \bm{X}. \end{aligned}$$

最終的に固有ベクトルや固有値が消えて、正規化された隣接行列の $k$ 乗で表現することができました。この形はランダムウォークとも深い関わりがありますし、personalized PageRank といった指標の計算にも似た形が出現するため、様々な関連モデルが研究されています。

理論的な枠組みの概要については確認できたので、一つ一つのモデルを確認していきましょう。

Spectral Networks ^[9]

こちらの手法ではフィルター $\bm{g}_w$ を以下のように定義します。

$$\bm{g}_w := diag(\bm{w})$$

この時 $\bm{w} \in \mathbb{R}^N$ はパラメータです。

固有値分解を必要を必要とするため計算量が $O(N^3)$ になるなど、この手法は計算効率が悪いうえ、フィルターにも問題がある点などが指摘されています。そのため、後に様々な改善モデルが提案されています

ChebNet ^[10][11]

ChebNet では、フィルター $\bm{g}_w$ をチェビシェフの多項式(Chebyshev polynomials) $\bm{T}_k(x)$ による展開のうち、$K$次の項までを用いて近似します。

$$\bm{g}_w \ast \bm{x} \simeq \sum_{k=0}^{K} w_k \bm{T}_k(\~{\bm{L}}) \bm{x}$$

ここでチェビシェフの多項式は以下のように定義されるものです。

$$\bm{T}_k(\bm{x})= 2\bm{x}\bm{T}_{k-1}(\bm{x}) - \bm{T}_{k-2}(\bm{x})$$

$$\bm{T}_{0}(\bm{x}) = 1, \bm{T}_{1}(\bm{x}) = \bm{x}$$

これにより、ラプラシアン行列の固有ベクトルを用いる必要がなくなり、計算量を削減することが可能になりました（固有値分解には $O(N^3)$ の計算量が必要）。

GCN(Graph Convolutional Network)^[12]

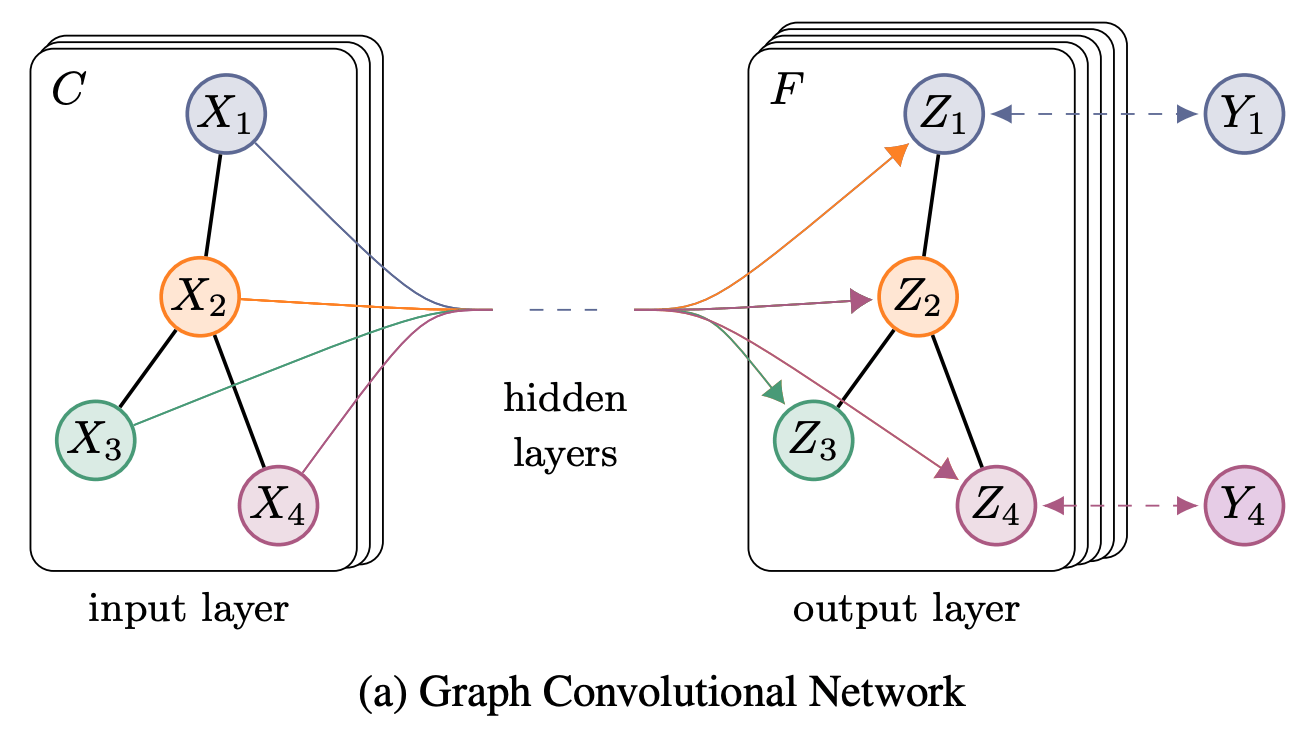
(画像引用元：Thomas N. Kipf, and Max Welling 2017, Figure 1(a) ^[12:1])

ChebNet における $K=1$ の場合を考えたケースが Kipf,Welling らによって提案された GCN(Graph Convolutional Network) です。

$\lambda_{max} \simeq 2$ と仮定することで、以下のように簡略化しています。

$$\begin{aligned} \bm{g}_w &\ast \bm{x} \simeq w_0 \bm{x} + w_1 (\bm{L}-\bm{I})\bm{x}\\ &= w_0 \bm{x} - w_1 \bm{D}^{-1/2}\bm{A}\bm{D}^{-1/2} \bm{x} \end{aligned}$$

さらに、パラメータに $w=w_0=-w_1$ という制約を加えることで、更にシンプルな形で表現することができます。また、各頂点に自己ループを加えた形を考えると隣接行列は $\~{\bm{A}}=\bm{A}+\bm{I}$ と表現できます。このときの次数行列を $\~{\bm{D}}$ とすると、

$$\begin{aligned} \bm{g}_w &\ast \bm{x} \simeq w(\bm{I} + \bm{D}^{-1/2}\bm{A}\bm{D}^{-1/2}) \bm{x}\\ &= w(\~{\bm{D}}^{-1/2}\~{\bm{A}}\~{\bm{D}}^{-1/2}) \bm{x} \end{aligned}$$

ここまでシンプルな形にまとめると、グラフの特徴行列 $\bm{X} \in \mathbb{R}^{N \times D}$ をつかって、簡潔な形で表現することができます。

$$\bm{H} = \~{\bm{D}}^{-1/2}\~{\bm{A}}\~{\bm{D}}^{-1/2} \bm{X} \bm{W}$$

ここで、$\bm{W} \in \mathbb{R}^{D \times D'}$ はパラメータであり、$\bm{H} \in \mathbb{R}^{N \times D'}$ は畳み込み後の特徴を表した行列になります。

このモデルは、後述する Spatial な GNN モデルともみなすこともできるため、非常に重要な立ち位置になっています。ちょうどこの論文が出たあたりから、Spatial な手法がメインになっていく流れがあるように感じます。

Approximate Personalized Propagation of Neural Predictions (APPNP)^[13]

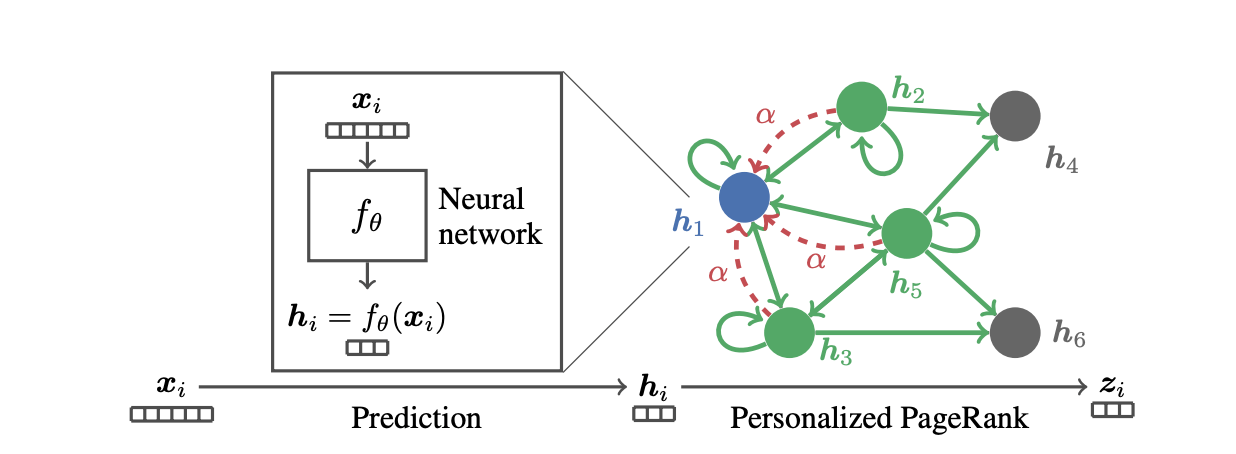
(画像引用元：Johannes Gasteiger, Aleksandar Bojchevski, and Stephan Günnemann 2019, Figure 1 ^[13:1])

personalized PageRank と呼ばれる値を利用した GNN のモデルとして有名なものに、APPNP(Approximate Personalized Propagation of Neural Predictions) があります。

まず最初にNNを適用してそれぞれの頂点から特徴量を抽出したあと、行列の掛け算を通して特徴量を集約します。

同論文中に提案された PPNP と呼ばれるモデルを近似したものですが、以下のような計算を行います。

$$\begin{aligned} \bm{Z}^{(0)} & = \bm{H} = \psi(\bm{X}), \\ \bm{Z}^{(k+1)} & = (1-\alpha)\~{\bm{A}}\bm{Z}^{(k)}+\alpha \bm{H},\\ \bm{Z}^{(K)} & = (1-\alpha)\~{\bm{A}}\bm{Z}^{(K-1)}+\alpha \bm{H}. \end{aligned}$$

厳密な形では無くなってしまいますが、このモデルを少し変形することで、Spectral Graph Neural Network の一種とみなすことが可能です。

$$\bm{Z} = \sum_{k=0}^{K}\alpha(1-\alpha)^k \~{\bm{A}}^k \bm{H}.$$

このモデルから着想を得て、大規模グラフにスケールさせるためのモデルなどがいくつか提案されていたりします。

Spatial な GNN モデル

ある頂点を中心に見た時に、その近傍の頂点の情報を利用する GNN のことを Spatial GNN と言います。

Spatial なモデルの説明としてよく使われるのは、「グラフのトポロジーを利用している」からspatial だという説明でしょうか。ここで言うトポロジーが何を指しているのか曖昧ですが、「グラフの頂点同士の繋がり方」くらいの意味で捉えておいても十分だと思います。

分類の仕方は様々ありますが、ここでは代表的なものとして以下の3種類を紹介します。

• Convolutional
• Attentional
• Message-passing

単純なものとして Convolutional なものを紹介し、Convolutional < Attentional < Message-passing と抽象度が上がっていきます。

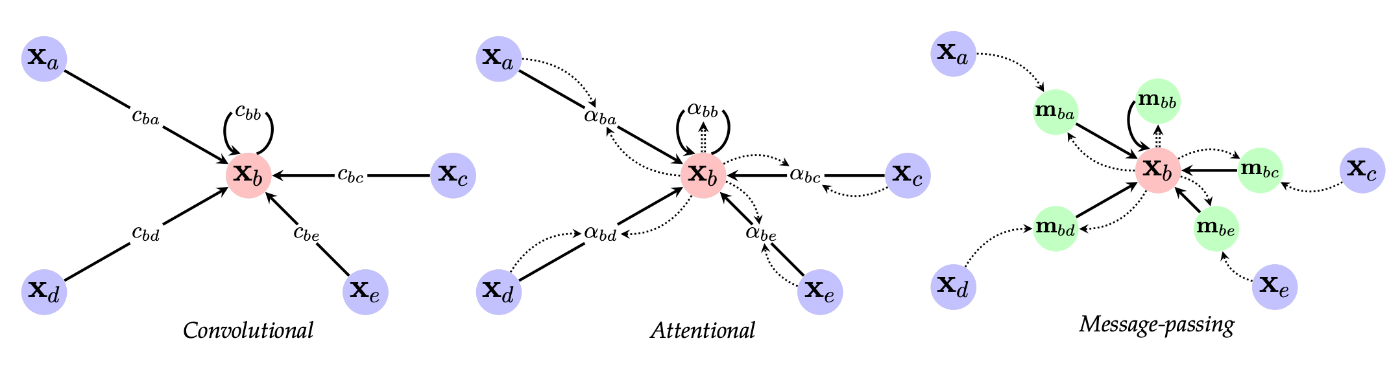
(画像引用元：Bronstein, M.M., Bruna, J., Cohen, T. and Veličković, P., 2021, Figure 17 ^[14])

Convolution を利用したモデル^[11:1][12:2]

Kipf,Welling らによって Spectral GNN として言及されていたモデルですが、グラフ構造上で畳み込むモデルとしてもみなすことができます。

一般化すると畳み込み1層分の演算は以下のような形になります。

$$\bm{h}_u = \phi \left( \bm{x}_u, \bigoplus_{v\in N_u} c_{uv} \psi(\bm{x}_v) \right)$$

• $c_{uv}$ : 頂点 $v$ の $u$ に対する重要度を表します（定数で、隣接行列 $\bm{A}$ の要素に依存していることが多い）
• $\psi$ や $\phi$ : ニューラルネットワークを意味しています（例：$\psi(\bm{x}) = \text{ReLU}(\bm{Wx}+\bm{b})$ ）
• $\bigoplus$ : 順序に関して不変な何かしらの集約を表しています（例：sum, average, max）

Attention を利用したモデル^[15]

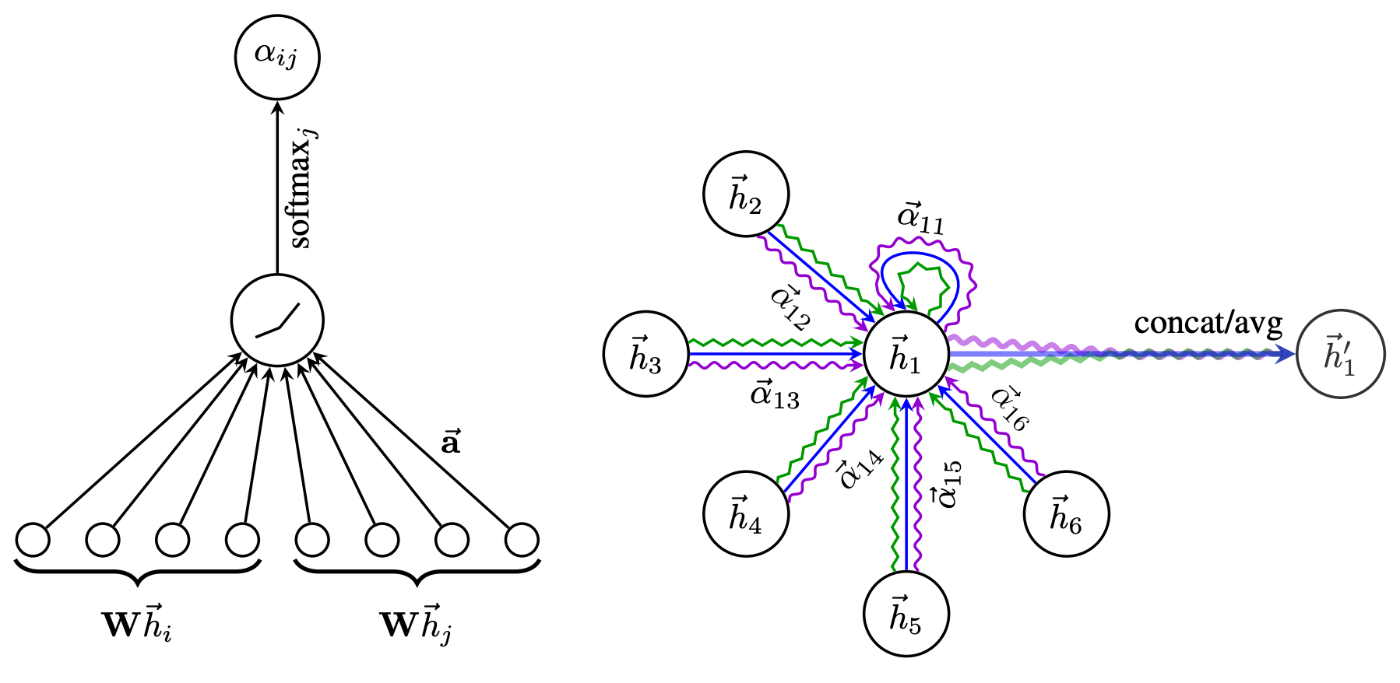
(画像引用元：Petar Veličković, Guillem Cucurull, Arantxa Casanova, Adriana Romero, Pietro Liò, and Yoshua Bengio 2018, Figure 1 ^[15:1])

通常の畳み込みとは一味違うモデルとして、attention機構を取り入れたモデルも存在します。単純な GCN よりは良い性能であることが多いようです。

$$\bm{h}_u = \phi \left( \bm{x}_u, \bigoplus_{v\in N_u} a(\bm{x}_u, \bm{x}_v) \psi(\bm{x}_v) \right)$$

• $a(\bm{x}_u, \bm{x}_v)$ : 学習可能な attention 機構。重要度を非明示的に決定する。入力を結合してself-attentionに入れ、出力は全近傍間について softmax で normalize されることが多い。

元論文では単層の順伝播型ニューラルネットワークを attention として採用しており、入力には $\bm{x}_u, \bm{x}_v$ に学習可能な行列をかけて変換してから結合したものを入れていました。attention部分を定数とすると、さきほどの Convolution を利用したモデルと同一視することもできます。

Message-passing フレームワーク^[16]

最後が message-passing フレームワークと呼ばれるものです。これは上述２つのモデルを含むような統一的な定義をしているためモデルと言うよりもフレームワークとして扱われます。

既存のモデルを再構築し、 message passing phase と readout phase と呼ばれる2つのフェーズからなる形へ一般化したものになります。

message passing phase で特徴量の伝搬と集約を行い、readout phase で得られた情報を最終的な予測へ変換します。

特に message passing phase は以下の形で表現することができます。

$$\bm{h}_u = \phi \left( \bm{x}_u, \bigoplus_{v\in N_u} \psi(\bm{x}_u, \bm{x}_v) \right)$$

message-passing というキーワードは良く出てくるので覚えておくと良いでしょう。

サンプリングを利用したモデル

Spacial GNN にも課題がいくつかあります。一つには、畳み込みの層を深くしていくと一つの頂点のために情報を集約する必要のある近傍の数は深さに応じて指数関数的に増えていくという問題があります。これを「近傍爆発(neighbor explosion)」と呼ぶことがあります。使う頂点数が多くなりすぎてしまうと、集約結果がどの頂点でも似たようなものになってしまう「過剰平滑化問題(oversmoothing problem)」にも繋がることがあります。

また、そのままだと大規模なグラフを扱うのも苦手です。初期の spectral graph neural network などのような固有値分解が求められるモデルと比べると計算コストは抑えられるようになってきています。それでも頂点や辺の数が多くなってくると、近傍情報を常に保存し続けることも難しくスケーラビリティの課題が出てきます。

以上の問題に対応するためのモデルとして以下のようなサンプリングを用いたものがあります。

• Node sampling: 集約する頂点をサンプリング
• Layer sampling: 各層で集約のための小さなノード集合を保持
• Subgraph sampling: 複数のサブグラフをサンプリングして、そのなかで学習を行う

Node samplingのモデル： GraphSAGE^[17]

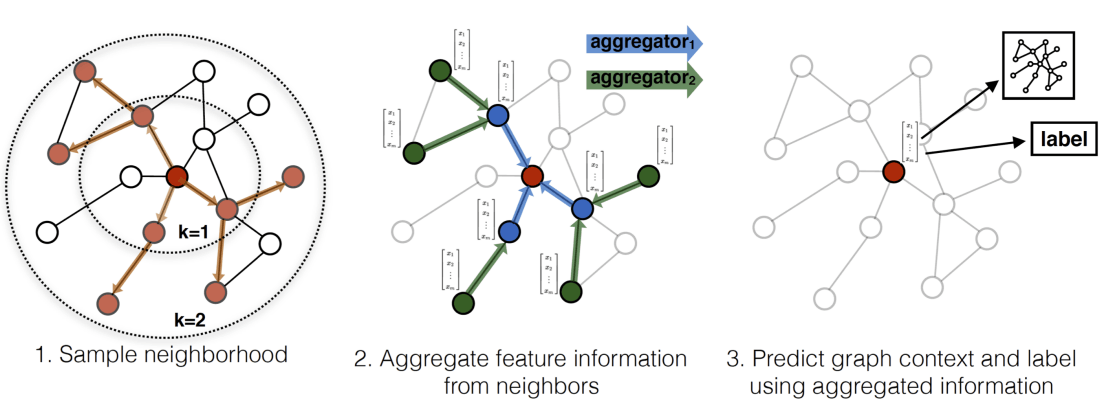
(画像引用元: Hamilton, W., Ying, Z., and Leskovec, J. 2017, Figure 1 ^[17:1])

(画像引用元: Hamilton, W., Ying, Z., and Leskovec, J. 2017, Algorithm 1 ^[17:2])

GraphSAGE は GCN を拡張した Spacial なモデルの一つです。各ノードについて個別の埋め込みを学習するかわりに、イテレーションごとに畳み込みに利用する頂点をサンプリングし集約関数を学習します。

sampling により、次数が大きい頂点に関しても計算量を一定に抑えることができるというメリットがあります。

また、「サンプリング→集約」という流れでノードの埋め込み表現を計算することにより、test 時の未知サブグラフに対しても、ノードの特徴量がわかっていれば埋め込み表現を計算することが可能です（inductiveな設定と呼ばれる。詳しくは後述）。

Layer sampling のモデル: FastGCN^[18]

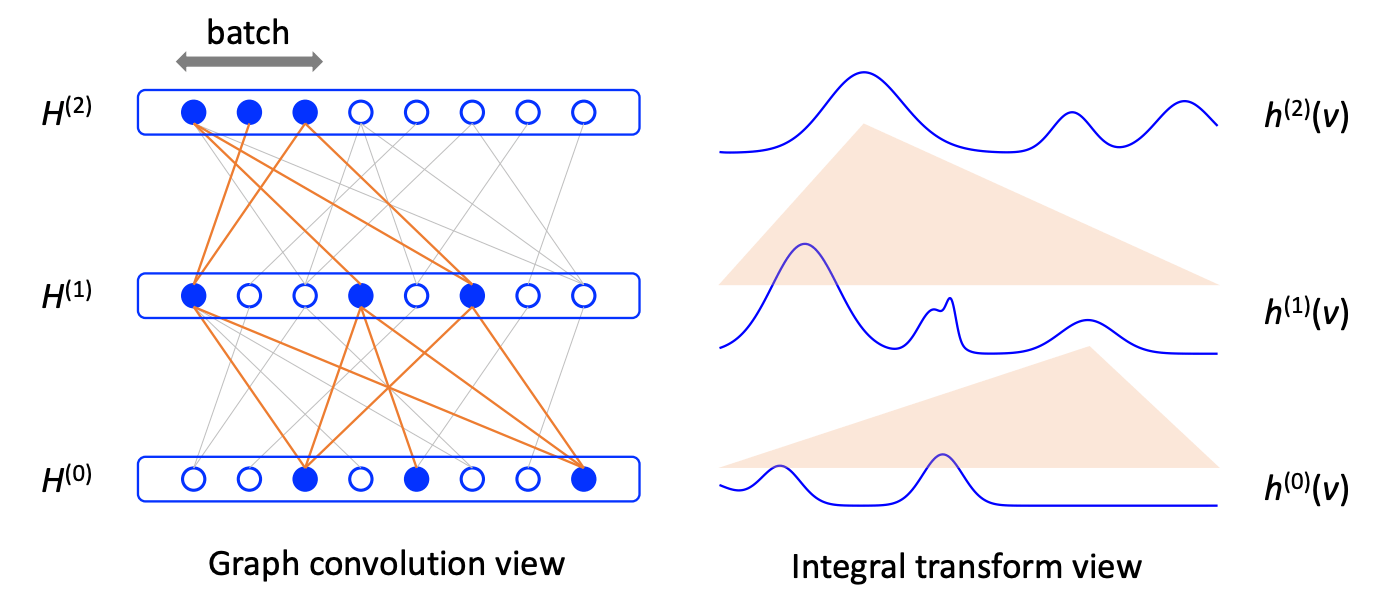
(画像引用元: Jie Chen, Tengfei Ma, and Cao Xiao 2018, Figure 1 ^[18:1])

FastGCNは各ノードに対して固定数の近隣ノードをサンプリングする代わりに、各グラフ畳み込み層に対して固定数のノードをサンプリングします。

図では、頂点が円で表されており、サンプリングされた部分は青い円とオレンジの線で示されています。

Subgraph sampling のモデル: ClusterGCN^[19]・GraphSAINT^[20]

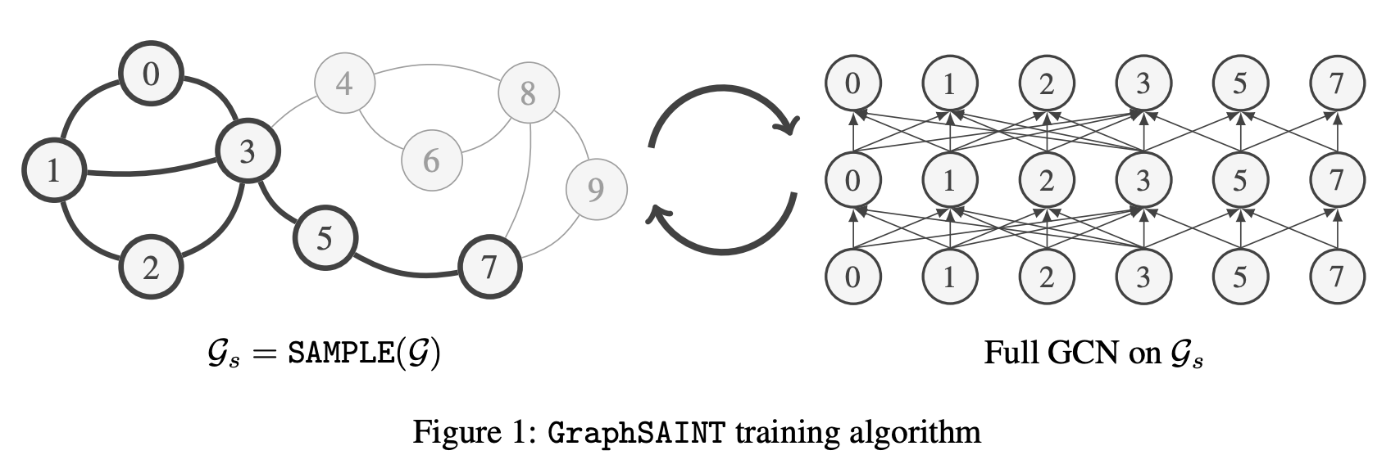
(画像引用元: Hanqing Zeng, Hongkuan Zhou, Ajitesh Srivastava, Rajgopal Kannan, and Viktor Prasanna 2020, Figure 1 ^[20:1])

サンプリング対象をサブグラフにしたモデルとして、ClusterGCN や GraphSAINT などのモデルがあります。

ClusterGCN はグラフをクラスタリングすることによってサブグラフをサンプリングし、GraphSAINT はサブグラフを生成するためにノードまたはエッジを直接サンプリングします。

その他のトピック

初期のGNN: Graph Recurrent Networks ^[21][22]

初期に提案されたGNNとして Graph Recurrent Networks があります。最初期では有向非巡回グラフに焦点が当てられていたようです。

概念的に重要であり、メッセージパッシングの考え方は後のSpacialなGNNに受け継がれています。ただ、安定した状態に達するまで、常に近隣のノードと情報/メッセージを交換し続けるとしているため計算時間は多くなってしまうという課題がありました。

具体的には以下の形で更新します。

$$\bm{h}_v^t = \sum_{u \in N(v)} \phi(\bm{x}_v, \bm{x^e}_{(u,v)},\bm{x}_u, \bm{h}_u^{t-1})$$

ここで、$\bm{h}_v^t$ は $t$回目に集約された情報を表し、$\bm{x^e}_{(u,v)}$ はエッジの特徴量を表します。

GCN の改良系： GCNII^[23]

サンプリングを利用せずに「過剰平滑化問題(oversmoothing problem)」に対処したモデルとして GCNII があります。このモデルは、Initial residual と Identity mapping の2つのシンプルな手法を用いて、バニラGCNモデルを拡張しています。

ResNetのように直前の層からのシンプルなスキップコネクションを導入することはあまり効果が無いことが知られていましたが、Initial residual では一番初めの層からの接続を作ります。これにより、最終層からの出力であっても、入力層からの情報を一部保持していることが保証されるため、性能の劣化を防ぐことができます。

また、Identity mappingは、各層の重み行列に対して単位行列を加えます。これも ResNet からの着想を得て加えたものです。

層を深くしても問題ないため、よりディープなモデルにすることによって表現力が向上し、多くのモデルを上回る性能を示しているようです。

inductive task か transductive task か

node classification を行う場合は学習時に評価用の頂点を用いるかどうかでタスク設定が分かれます。ラベル情報はリークになってしまうのでもちろん使えませんが、実際にその頂点が存在していて学習に使いたい頂点との辺がある場合はその接続しているという情報は有用です。

この設定の違いは inductive か transductive かで分かれます。実際に用いる際はどちらの設定を想定されているのかに注意しておくと良いでしょう。

• inductive node classification tasks
  • モデルの学習にはラベル付けされたノードのみを用いる
  • ラベル付けされていないデータについて予測
• transductive node classification tasks
  • ラベル付けされたノードと評価用のラベル付けされていないノードの両方をモデルの学習に用いる

GraphSAGE^[17:3] は inductive でも使えるモデルとして提案されたという側面もあります。

GNNの実装方法

ライブラリの種類

実際にGNNの実装をする場合は、PyTorchやTensorFlowなどの機械学習ライブラリを用いて自分で実装することもできますが、それらをベースに構築されたGNNのライブラリを用いると比較的簡単に実装することができます。

GNNのライブラリとしては有名なものが２つあります。

• PyTorch Geometric (PyG)
  • PyTorch とスパース用列を扱うための拡張ライブラリに基づいている
  • PyTorchの利用経験があれば扱いやすい
• Deep Graph Library (DGL)
  • PytorchとTensorFlowのいずれかをバックエンドとして利用可能

記事作成時点では、PyTorch Geometric のほうが GitHub のスター数が多く人気があるようです。
（GNNの分野はまだまだ発展途上のこともあり、最新手法や使いたいモデルが反映されていないことがあります。それらを用いたい場合は論文と公開されたコードを参考に自分で実装する必要があることにも注意してください。）

今回は、PyTorch Geometirc を用いて Semi-Supervised Node Classification を行うコードを通して、どのように実装するのか確認してみましょう。
PyTorch Geometirc のバージョンによってコードの書き方などが変わる可能性があるので注意してください。今回はPyTorch のバージョンは2.0.1+cu118, PyTorch　Geometric のバージョンは 2.4.0 を用いることとします。

PyTorch Geometric のインストール

Colaboratory 上で PyTorch Geometric を実行する方法について見ていきます。まずはバージョン確認とPyTorch Geoemtric のインストールを行いましょう。

import torch
print(torch.__version__)

# Install required packages.
import os
os.environ['TORCH'] = torch.__version__

!pip install torch-scatter -f https://data.pyg.org/whl/torch-${TORCH}.html
!pip install torch-sparse -f https://data.pyg.org/whl/torch-${TORCH}.html
!pip install pyg-lib -f https://data.pyg.org/whl/nightly/torch-${TORCH}.html
!pip install git+https://github.com/pyg-team/pytorch_geometric.git

ここで、torch-scatter,torch-sparse,pyg-lib は疎行列などを扱うためのPyTorchの拡張ライブラリで、Pytorch Geometircの内部で利用されることがあるため予めインストールしておきます（PyGの使い方によっては不要なライブラリもあります）。

データセットの準備

Citation Network として CiteSeer データセットを利用します。よく論文などで用いられるようなデータについては、予め PyG でクラスが用意されており簡単にダウンロードすることができます。

from torch_geometric.datasets import Planetoid
from torch_geometric.transforms import NormalizeFeatures

dataset = Planetoid(root='data/Planetoid', name='CiteSeer', transform=NormalizeFeatures())

data = dataset[0]  

print()
print(data)

Downloading https://github.com/kimiyoung/planetoid/raw/master/data/ind.citeseer.x
Downloading https://github.com/kimiyoung/planetoid/raw/master/data/ind.citeseer.tx
Downloading https://github.com/kimiyoung/planetoid/raw/master/data/ind.citeseer.allx
Downloading https://github.com/kimiyoung/planetoid/raw/master/data/ind.citeseer.y
Downloading https://github.com/kimiyoung/planetoid/raw/master/data/ind.citeseer.ty
Downloading https://github.com/kimiyoung/planetoid/raw/master/data/ind.citeseer.ally
Downloading https://github.com/kimiyoung/planetoid/raw/master/data/ind.citeseer.graph
Downloading https://github.com/kimiyoung/planetoid/raw/master/data/ind.citeseer.test.index
Processing...
Done!

Data(x=[3327, 3703], edge_index=[2, 9104], y=[3327], train_mask=[3327], val_mask=[3327], test_mask=[3327])

Planetoid は citation network の dataset を用いるためのクラスで ^[24] の論文に基づいています。他に "Cora" "PubMed"などのデータセットを用いることができます。

NormalizeFeatures は頂点ごとに存在する 3703 次元の特徴量を正規化してくれます。

dataset は複数の data から構成されますが、今回は一つしかないのであまり気にする必要はありません。

Data はグラフのデータを表すクラスとなっています。

グラフの情報をいくつか確認すると以下のようになります。

print(f'頂点数: {data.num_nodes}')
print(f'辺数: {data.num_edges}')
print(f'平均次数: {data.num_edges / data.num_nodes:.2f}')
print(f'Train用の頂点数: {data.train_mask.sum()}')
print(f'self-loopを持つか: {data.has_self_loops()}')
print(f'無向グラフかどうか: {data.is_undirected()}')

頂点数: 3327
辺数: 9104
平均次数: 2.74
Train用の頂点数: 120
self-loopを持つか: False
無向グラフかどうか: True

モデル構築と学習

シンプルなGCNを使ったモデルを使って学習してみましょう。
PyTorch Geometric は通常の PyTorchと似た形でモデルを定義し学習することが可能です。

import torch.nn.functional as F
from torch_geometric.nn import GCNConv

class GCN(torch.nn.Module):
    def __init__(self, hidden_channels, dropout=0.0):
        super().__init__()
        torch.manual_seed(1)
        self.conv1 = GCNConv(dataset.num_features, hidden_channels)
        self.conv2 = GCNConv(hidden_channels, dataset.num_classes)
        self.dropout = dropout

    def forward(self, x, edge_index):
        x = F.dropout(x, self.dropout, training=self.training)
        x = self.conv1(x, edge_index)
        x = x.relu()
        x = F.dropout(x, self.dropout, training=self.training)
        x = self.conv2(x, edge_index)
        return x

GCNConv 以外にも GCNII^[23:1]を元にしたGCN2Convや、Attenntionを利用した GATConv や GATv2Conv など様々なレイヤーが存在するので、これらを利用したモデルを構築することも可能です。
詳細はドキュメントのtorch_geometric.nn — pytorch_geometric documentation を確認すると良いでしょう。

モデルが定義できたら、学習と評価をしてみましょう。

device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')
model = GCN(hidden_channels=64, dropout=0.5).to(device)
data = data.to(device)
optimizer = torch.optim.Adam(model.parameters(), lr=0.01, weight_decay=5e-4)
criterion = torch.nn.CrossEntropyLoss()

def train():
      model.train()
      optimizer.zero_grad()
      out = model(data.x, data.edge_index)  
      loss = criterion(out[data.train_mask], data.y[data.train_mask]) 
      loss.backward()
      optimizer.step()
      return loss

def test():
      model.eval()
      out = model(data.x, data.edge_index)
      pred = out.argmax(dim=1)
      accs = []
      for _, mask in data('train_mask', 'val_mask', 'test_mask'):
          accs.append(int((pred[mask] == data.y[mask]).sum()) / int(mask.sum()))
      return accs

best_val_acc = test_acc = 0
for epoch in range(1, 1001):
    loss = train()
    train_acc, val_acc, tmp_test_acc = test()
    if val_acc > best_val_acc:
        best_val_acc = val_acc
        test_acc = tmp_test_acc
    print(f'Epoch: {epoch:04d}, Train: {train_acc:.4f}, '
          f'Val: {val_acc:.4f}, '
          f'Test: {test_acc:.4f}')

Epoch: 0001, Train: 0.1667, Val: 0.1880, Test: 0.1690
Epoch: 0002, Train: 0.4417, Val: 0.2120, Test: 0.1910
Epoch: 0003, Train: 0.7333, Val: 0.2920, Test: 0.2890
Epoch: 0004, Train: 0.8583, Val: 0.3840, Test: 0.3830
Epoch: 0005, Train: 0.8583, Val: 0.4140, Test: 0.3980
Epoch: 0006, Train: 0.8667, Val: 0.4040, Test: 0.3980
Epoch: 0007, Train: 0.9000, Val: 0.4120, Test: 0.3980
Epoch: 0008, Train: 0.9083, Val: 0.4780, Test: 0.4630
︙
Epoch: 0994, Train: 1.0000, Val: 0.7080, Test: 0.7140
Epoch: 0995, Train: 1.0000, Val: 0.7120, Test: 0.7140
Epoch: 0996, Train: 1.0000, Val: 0.7200, Test: 0.7140
Epoch: 0997, Train: 1.0000, Val: 0.7200, Test: 0.7140
Epoch: 0998, Train: 1.0000, Val: 0.7160, Test: 0.7140
Epoch: 0999, Train: 1.0000, Val: 0.7160, Test: 0.7140
Epoch: 1000, Train: 1.0000, Val: 0.7040, Test: 0.7140

最後に

グラフの説明から始まり、様々なモデルについてご紹介しましたが、まだまだ説明しきれていないものが多くあります。また、日々新しいモデルや活用方法が提案されておりまだまだ発展途上の段階とも言えます。

グラフ自体にも様々な種類があるため、二部グラフに特化したGNNや、異種グラフ(heterophilic graphs)に特化したGNNなど様々なモデルが存在します。このような特化モデルが存在するのも複雑になる要因の一つでしょう。

また、現状は産業的に上手く活用できた事例は少ないように見られます。これは、1 hop 近傍の情報だけを利用したGNN以外のモデルがかなり良い性能を出すことが多いというのも理由としてあげられるかもしれません。
これは現状のGNNの仕組み上致し方ない側面もあり、複数 hop 先までの高次の接続情報が予測に対して重要な役割を担っていないとあまり効果がないと考えられます。

最後まで閲覧ありがとうございました。
本記事が理解の一助になれば幸いです。

参考になる資料

• 【ネットワークの統計解析】第7回　グラフラプラシアン・グラフフーリエ変換を簡単に振り返る
• グラフ信号処理のすゝめ
• Heterogeneous Graphでグラフニューラルネットワークの学習をやってみた

脚注

1. Wu, Z., Pan, S., Chen, F., Long, G., Zhang, C. and Philip, S.Y., 2020. A comprehensive survey on graph neural networks. IEEE transactions on neural networks and learning systems, 32(1), pp.4-24.

2. Filipowski, T., Kazienko, P., Brodka, P. and Kajdanowicz, T., 2012. Web-based knowledge exchange through social links in the workplace. Behaviour & Information Technology, 31(8), pp.779-790.

3. Hu, Z., Shao, F. and Sun, R., 2022. A New Perspective on Traffic Flow Prediction: A Graph Spatial-Temporal Network with Complex Network Information. Electronics, 11(15), p.2432.

4. Veličković, P., 2023. Everything is connected: Graph neural networks. Current Opinion in Structural Biology, 79, p.102538.

5. Zhou, J., Cui, G., Hu, S., Zhang, Z., Yang, C., Liu, Z., Wang, L., Li, C. and Sun, M., 2020. Graph neural networks: A review of methods and applications. AI open, 1, pp.57-81.

6. Stocker, S., Csányi, G., Reuter, K. and Margraf, J.T., 2020. Machine learning in chemical reaction space. Nature communications, 11(1), p.5505.

7. Wang, S., Hu, L., Wang, Y., He, X., Sheng, Q.Z., Orgun, M.A., Cao, L., Ricci, F. and Yu, P.S., 2021. Graph learning based recommender systems: A review. arXiv preprint arXiv:2105.06339.

8. Shuman, D.I., Narang, S.K., Frossard, P., Ortega, A. and Vandergheynst, P., 2013. The emerging field of signal processing on graphs: Extending high-dimensional data analysis to networks and other irregular domains. IEEE signal processing magazine, 30(3), pp.83-98.

9. Bruna, J, Zaremba, W, Szlam, A & Lecun, Y 2014, Spectral networks and locally connected networks on graphs. in International Conference on Learning Representations (ICLR2014), CBLS, April 2014., http://openreview.net/document/d332e77d- 459a-4af8-b3ed-55ba9662182c, http://arxiv.org/abs/1312.6203.

10. Hammond, D.K., Vandergheynst, P. and Gribonval, R., 2011. Wavelets on graphs via spectral graph theory. Applied and Computational Harmonic Analysis, 30(2), pp.129-150.

11. Defferrard, M., Bresson, X. and Vandergheynst, P., 2016. Convolutional neural networks on graphs with fast localized spectral filtering. Advances in neural information processing systems, 29.

12. Thomas N. Kipf, and Max Welling 2017. Semi-Supervised Classification with Graph Convolutional Networks. In International Conference on Learning Representations.

13. Johannes Gasteiger, Aleksandar Bojchevski, and Stephan Günnemann 2019. Combining Neural Networks with Personalized PageRank for Classification on Graphs. In International Conference on Learning Representations.

14. Bronstein, M.M., Bruna, J., Cohen, T. and Veličković, P., 2021. Geometric deep learning: Grids, groups, graphs, geodesics, and gauges. arXiv preprint arXiv:2104.13478.

15. Petar Veličković, Guillem Cucurull, Arantxa Casanova, Adriana Romero, Pietro Liò, and Yoshua Bengio 2018. Graph Attention Networks. In International Conference on Learning Representations.

16. Gilmer, J., Schoenholz, S.S., Riley, P.F., Vinyals, O. and Dahl, G.E., 2017, July. Neural message passing for quantum chemistry. In International conference on machine learning (pp. 1263-1272). PMLR.

17. Hamilton, W., Ying, Z., and Leskovec, J. 2017. Inductive representation learning on large graphs. Advances in neural information processing systems, 30.

18. Jie Chen, Tengfei Ma, and Cao Xiao 2018. FastGCN: Fast Learning with Graph Convolutional Networks via Importance Sampling. In International Conference on Learning Representations.

19. Chiang, W.L., Liu, X., Si, S., Li, Y., Bengio, S. and Hsieh, C.J., 2019, July. Cluster-gcn: An efficient algorithm for training deep and large graph convolutional networks. In Proceedings of the 25th ACM SIGKDD international conference on knowledge discovery & data mining (pp. 257-266).

20. Hanqing Zeng, Hongkuan Zhou, Ajitesh Srivastava, Rajgopal Kannan, and Viktor Prasanna 2020. GraphSAINT: Graph Sampling Based Inductive Learning Method. In International Conference on Learning Representations.

21. Sperduti, A. and Starita, A., 1997. Supervised neural networks for the classification of structures. IEEE Transactions on Neural Networks, 8(3), pp.714-735.

22. Scarselli, F., Gori, M., Tsoi, A.C., Hagenbuchner, M. and Monfardini, G., 2008. The graph neural network model. IEEE transactions on neural networks, 20(1), pp.61-80.

23. Chen, M., Wei, Z., Huang, Z., Ding, B. and Li, Y., 2020, November. Simple and deep graph convolutional networks. In International conference on machine learning (pp. 1725-1735). PMLR.

24. Yang, Z., Cohen, W. and Salakhudinov, R., 2016, June. Revisiting semi-supervised learning with graph embeddings. In International conference on machine learning (pp. 40-48). PMLR.