Two Player's Quantum Covert Lottery

日本語版: https://zenn.dev/yyu/articles/79c6c48226166aa0e875

Introduction

The word “covert lottery” is a security protocol introduced by Card-Based Covert Lottery^[1]. In this protocol, there are two players and they input each secret request then:

1. If these two requests are not the same, the protocol approve their requests
2. Otherwise the requests are the same, the protocol decides either one player's request at random

For example, in Chess game we can use covert lottery to determine if the players take the first move or the second move. These players have their requests but since one's request would be known by the other player, the strategy maybe leak. Covert lottery protocol outputs the actual their requests as long as the requests are not the same, and otherwise it outputs a random result. Both players cannot know if the output reflects their requests or random so there is no information leak.
In the original paper, the protocol is implemented using card-based cryptography^[2].I read it and I think it also can be done using quantum technics. So I'll show that the quantum version of covert lottery protocol in this article.

Discussions and questions are very welcome! If you have something you want to ask, please let me know about it.

Two Players Covert Lottery Function

At first I explain about covert lottery in the original paper. There are two players: whose name are Alice and Bob. Alice input is $a$, and she wants to take the first move then $a = 1$ and wants to take the second move then $a = 0$. Similarly Bob wants to take the first move then $b = 1$ and wants to take the second move then $b = 0$. And $\mathcal{F}$ is the function which outputs Alice's move. It means that if $\mathcal{F}$ outputs $1$ then Alice takes the first move, or the output would be $0$ she takes the seconds move. $\mathcal{F}$ can be defined as follows.

$$\mathcal{F}(a, b) := \left\{ \begin{array}{lr} a & \text{if}\; a \ne b \\ i \xleftarrow{\text{rnd}} \{0, 1\} & \text{if}\; a = b \end{array} \right.$$

Note that $\xleftarrow{\text{rnd}} \{0, 1\}$ means to chose from $\{0, 1\}$ at random. And I introduce a notation $\overline{x}$ which means binary NOT operation for $x \in \{0,1\}$.

Considering $\mathcal{F}$, if $a \ne b$ the $a = \overline{b}$. And if $a = b$ then $\{a, \overline{b}\} = \{0, 1\}$. So $\mathcal{F}$ can be simplified as follows.

$$\mathcal{F}(a, b) = \left\{ \begin{array}{lr} a\, (= \overline{b}) & \text{if}\; a \ne b \\ i \xleftarrow{\text{rnd}} \{a, \overline{b}\} & \text{if}\; a = b \end{array} \right.$$

In case of $a \ne b$, it actually equals to select one randomly from $\{a, \overline{b}\}$. Finally it isn't necessarily to divide into two cases.

$$\mathcal{F}(a, b) = r \xleftarrow{\text{rnd}} \{a, \overline{b}\}$$

Quantum Covert Lottery based on BB84

I show that the naive protocol using quantum computer at first.

This protocol is vulnerable!

Protocol

1. Alice generates 1 bit random $x \xleftarrow{\text{rnd}} \{0, 1\}$ and chose her request $a \in \{0, 1\}$

2. Alice decides 1 qubit $\ket{\psi_{a,x}}$ of the following four qubits by $a, x$

   $$\def\bra#1{\mathinner{\left\langle{#1}\right|}} \def\ket#1{\mathinner{\left|{#1}\right\rangle}} \left\{ \begin{array}{lcl} \ket{\psi_{0,0}} & \equiv & \ket{0} \\ \ket{\psi_{0,1}} & \equiv & \ket{1} \\ \ket{\psi_{1,0}} & \equiv & \ket{+} \\ \ket{\psi_{1,1}} & \equiv & \ket{-} \end{array} \right.$$
   • where $\ket{\pm} \equiv \frac{1}{\sqrt{2}}\left(\ket{0} \pm \ket{1}\right)$

3. Alice sends $\ket{\psi_{a,x}}$ to Bob

4. Bob receives $\ket{\psi_{a,x}}$ and chose his request $b \in \{0, 1\}$

5. Bob select the ground state $\mathcal{B}_{\overline{b}}$, mesures $\ket{\psi_{a,x}}$ by it. He measures the qubit and the result store into $y$

   $$\mathcal{B}_{\overline{b}} \equiv \left\{\ket{\psi_{\overline{b},0}}, \ket{\psi_{\overline{b},1}}\right\}$$
   • Note that it requires $\overline{b}$ rather than $b$

6. Bob sends $y$ to Alice

7. Alice receives $y$ and she sends $a \oplus x \oplus y$^[3] as final result to Bob

Description

The following table shows that $y$ and $a \oplus x \oplus y$ depending on Alice's inputs $a, x$ and Bob's input $b$.

$a$	$x$	$\ket{\psi_{a,x}}$	$\overline{b}$	$\mathcal{B}_{\overline{b}}$	$y$	$a \oplus x \oplus y$
$0$ (Second)	$0$	$\ket{0}$	$0$ (First)	$\left\{\ket{0}, \ket{1}\right\}$	$0$	$0$
$0$ (Second)	$0$	$\ket{0}$	$1$ (Second)	$\left\{\ket{+}, \ket{-}\right\}$	$r \xleftarrow{\text{rnd}} \{0, 1\}$	$r \xleftarrow{\text{rnd}} \{0, 1\}$
$0$ (Second)	$1$	$\ket{1}$	$0$ (First)	$\left\{\ket{0}, \ket{1}\right\}$	$1$	$0$
$0$ (Second)	$1$	$\ket{1}$	$1$ (Second)	$\left\{\ket{+}, \ket{-}\right\}$	$r \xleftarrow{\text{rnd}} \{0, 1\}$	$r \xleftarrow{\text{rnd}} \{0, 1\}$
$1$ (First)	$0$	$\ket{+}$	$0$ (First)	$\left\{\ket{0}, \ket{1}\right\}$	$r \xleftarrow{\text{rnd}} \{0, 1\}$	$r \xleftarrow{\text{rnd}} \{0, 1\}$
$1$ (First)	$0$	$\ket{+}$	$1$ (Second)	$\left\{\ket{+}, \ket{-}\right\}$	$0$	$1$
$1$ (First)	$1$	$\ket{-}$	$0$ (First)	$\left\{\ket{0}, \ket{1}\right\}$	$r \xleftarrow{\text{rnd}} \{0, 1\}$	$r \xleftarrow{\text{rnd}} \{0, 1\}$
$1$ (First)	$1$	$\ket{-}$	$1$ (Second)	$\left\{\ket{+}, \ket{-}\right\}$	$1$	$1$

The result $a \oplus x \oplus y$ equals to Alice's request $a$ where their requests are not the same. The reasons why it could be done are:

• Assuming that $a = \overline{b}\,(\Rightarrow a \ne b)$, in (5) the masurement $y$ is the same as Alice's random $x$
  • On the other hand, $y$ is a random value where $a \ne \overline{b}$ so $a \oplus x \oplus y$ is a random value too
• If $a = \overline{b}$ then $x = y$, therefore $x$ of $a \oplus x \oplus y$ is canceled by $y$ and the final result equals to $a$

Security Assumption

The final result of this protocol is calculated by Alice. If Alice is not honest she can change the result into what she wants. So the protocol works well under assuming that at least Alice is semi-honest.

Bob's request leakage

This naive protocol has a vulnerability that Alice can know the Bob's request in some cases. For example:

1. Alice select $a = 0, x = 0$ so she sends $\ket{0}$ to Bob
2. Bob choose $\overline{b} = 1\,(\Rightarrow b = 0)$
3. In the case, he measures using $\ket{0}$を$\left\{\ket{+}, \ket{-}\right\}$ then the output $y$ is $0$ or $1$ under the same probability
   • If $y = 0$ then there is no information leakage
4. But if $y = 1$ then Alice knows that $\overline{b} = 1$ because the output is $y = 0$ in 100% when measuring using $\left\{\ket{0}, \ket{1}\right\}$

The protocol result is valid as $\mathcal{F}$ but there is the problem that Alice can know the Bob's request in some cases.

CZ Gate and 1 Qubit Measurement-Based Quantum Computation

In this section, I introduce $CZ$ gate and measurement-based quantum computation

CZ Gate

$CZ$ gate is defined using $I, Z$ gates as follows^[4].

$$\begin{align*} CZ \equiv \ket{0}\bra{0}\otimes I + \ket{1}\bra{1}\otimes Z \\ \\ I \equiv \left(\begin{array}{cc} 1 & 0 \\ 0 & 1 \end{array}\right), \; Z \equiv \left(\begin{array}{cc} 1 & 0 \\ 0 & -1 \end{array}\right) \end{align*}$$

$CZ$ gate is two qubits operator and the behavior is:

• If the first qubit is $\ket{0}$ $CZ$ gate do nothing
• Otherwise $CZ$ gate apply $Z$ gate to the second qubit

For example, $\ket{\chi} := a\ket{0} + b\ket{1}$ and $\ket{+}$ are appended by $CZ$ gate.

$$\def\braket#1#2{\mathinner{\left\langle{#1}\middle|#2\right\rangle}} \begin{align*} CZ\ket{\chi}_1\ket{+}_2 &= \ket{0}\braket{0}{\chi}_1 I\ket{+}_2 + \ket{1}\braket{1}{\chi}_1 Z\ket{+}_2 \\ &= \ket{0}\braket{0}{\chi}_1 \ket{+}_2 + \ket{1}\braket{1}{\chi}_1 \ket{-}_2 \\ &= a\ket{0}_1\ket{+}_2 + b\ket{1}_1\ket{-}_2 \end{align*}$$

Note that: the $1, 2$ of the qubits means index.

1 Qubit Measurement-Based Quantum Computation

Considering the measurement of $CZ\ket{\chi}_1\ket{+}_2$, normally we use $\left\{\ket{0}, \ket{1}\right\}$ as ground state but we measure it by $\left\{\ket{0} \pm e^{i\phi}\ket{1}\right\}$ where $\phi$ is a arbitrary angle. Assuming that the result of the first qubit($\ket{\chi}_1$) masurement is $\ket{0} + e^{i\phi}\ket{1}$, the second qubit is as follows.

$$(\ket{0}_1 + e^{i\phi}\ket{1}_1)(\bra{0}_1 + e^{i\phi}\bra{1}_1) \cdot (a\ket{0}_1\ket{+}_2 + b\ket{1}_1\ket{-}_2) = (\ket{0}_1 + e^{i\phi}\ket{1}_1)(a\ket{+}_2 + be^{i\phi}\ket{-}_2)$$

And $a\ket{+}_2 + be^{i\phi}\ket{-}_2$ can be simplified like below:

$$\begin{align*} a\ket{+}_2 + be^{i\phi}\ket{-}_2 &= \frac{1}{\sqrt{2}}\left(a\ket{0} + a\ket{1} + be^{i\phi}\ket{0} - be^{i\phi}\ket{1}\right) \\ &= \frac{1}{\sqrt{2}}\left((a + be^{i\phi})\ket{0} + (a - be^{i\phi})\ket{1}\right) \end{align*}$$

Finally using Hadamard gate $H$ and phase shift gate $R_Z$.

$$\frac{1}{\sqrt{2}}\left((a + be^{i\phi})\ket{0} + (a - be^{i\phi})\ket{1}\right) = HR_Z(\phi)\ket{\chi}$$

If the result of the measurement is $\ket{0} - e^{i\phi}\ket{1}$, $X$ gate is added.

$$XHR_Z(\phi)\ket{\chi}$$

Definitions of Hadamard gate $H$, phase shift gate $R_Z$ and $X$ gate is as follows.

$$H \equiv \frac{1}{\sqrt{2}}\left(\begin{array}{cc} 1 & 1 \\ 1 & -1 \end{array}\right), \; R_Z(x) \equiv \left(\begin{array}{cc} 1 & 0 \\ 0 & e^{ix} \end{array}\right), \; X \equiv \left(\begin{array}{cc} 0 & 1 \\ 1 & 0 \end{array}\right)$$

Two Player's “Blind” Quantum Covert Lottery

This section is more complicated.

Protocol

1. Alice choose a random angle $\theta \xleftarrow{\text{rnd}} \left\{0, \frac{1\pi}{4}, \dots, \frac{7\pi}{4}\right\}$

2. Alice sends the following 1 qubit $\ket{+_\theta}$ to Bob

   $$\ket{+_\theta} \equiv \frac{1}{\sqrt{2}}\left(\ket{0} + e^{-i\theta}\ket{1}\right)$$

3. Bob apply $CZ$ gate to $\ket{+_\theta}$ received from Alice and $\ket{+}$

   $$CZ\ket{+_\theta}_1\ket{+}_2$$

   • $CZ\ket{+_\theta}_1\ket{+}_2$ can be simplified

     $$CZ\ket{+_\theta}_1\ket{+}_2 = \frac{1}{\sqrt{2}}\ket{0}_1\ket{+}_2 + \frac{e^{-i\theta}}{\sqrt{2}}\ket{1}_1\ket{-}_2$$

4. Alice choose her request $a \in {0, 1}$ and a random value $x \xleftarrow{\text{rnd}} \{0, 1\}$. And she sends the following angle $\delta$ to Bob

   $$\delta := \left\{ \begin{array}{ll} \theta + x\pi& \text{if}\; a = 0 \\ \theta + \frac{\pi}{2} + x\pi & \text{if}\; a = 1 \end{array} \right.$$

5. Bob prepares ground state $\left\{\ket{0} \pm e^{i\delta}\ket{1}\right\}$ using $\delta$ from Alice. And he measures the first qubit, and the result is $y$

6. Bob choose his request $b \in \{0, 1\}$ and decides a ground state $\mathcal{B}_{\overline{b}}$ depending on his request $b$

   $$\left\{ \begin{array}{lcl} \mathcal{B}_{0} & \equiv & \left\{\ket{\pm}\right\} \\ \mathcal{B}_{1} & \equiv & \left\{\frac{1}{\sqrt{2}}\left(\ket{0} \pm i\ket{1}\right)\right\} \end{array} \right.$$

7. Bob measures the second qubit using $\mathcal{B}_{\overline{b}}$ and the result is $z$. Then he sends $z$ to Alice

8. Alice outputs $a \oplus x \oplus z$ as the final result to Bob

Protocol Behavior

It's difficult to understand the procedure (5). The second qubit is as follows after Bob measured the first qubit using $\left\{\ket{0} \pm e^{i\delta}\ket{1}\right\}$.

1. In case $y = 0$

   $$\begin{align*} HR_Z(\delta)\ket{+_\theta} &= H\left(\ket{0} + e^{-i\theta}\cdot e^{i\delta}\ket{1}\right) \\ &= H\left(\ket{0} + e^{i(\delta - \theta)}\ket{1}\right) \end{align*}$$

2. In case $y = 1$

   $$XHR_Z(\delta)\ket{+_\theta} = XH\left(\ket{0} + e^{i(\delta - \theta)}\ket{1}\right)$$

This means that what the second qubit would be depends on $\delta - \theta$. The following table shows the second qubit depending on Alice's request $a$.

$a$	$x$	$\delta$	$y$	Second qubit
$0$	$0$	$\theta$	$0$	$H\ket{0} = \ket{+}$
$0$	$0$	$\theta$	$1$	$XH\ket{0} = \ket{+}$
$0$	$1$	$\theta + \pi$	$0$	$H\ket{1} = \ket{-}$
$0$	$1$	$\theta + \pi$	$1$	$XH\ket{1} = \ket{-}$
$1$	$0$	$\theta + \frac{\pi}{2}$	$0$	$H(\ket{0} + i\ket{1}$
$1$	$0$	$\theta + \frac{\pi}{2}$	$1$	$XH(\ket{0} + i\ket{1}$
$1$	$1$	$\theta + \frac{\pi}{2} + \pi$	$0$	$H(\ket{0} - i\ket{1})$
$1$	$1$	$\theta + \frac{\pi}{2} + \pi$	$1$	$XH(\ket{0} - i\ket{1})$

If $y = 1$ then the second qubit contains $X$ gate. You maybe think that it's necessary to remove this $X$ gate but actually it's not necessary. Assuming that the second qubit is $XH(\ket{0} + i\ket{1}) = \frac{1}{\sqrt{2}}\left(i\ket{0} + \ket{1}\right)$ then:

1. Bob's ground state is $\{\ket{\pm}\}$

   $$\ket{\pm}\bra{\pm}\left(\frac{1}{\sqrt{2}}(i\ket{0} + \ket{1})\right) = \left(\frac{1}{2}i \pm \frac{1}{2}\right)\ket{\pm}$$
   • The probability that the result would be $\ket{\pm}$ is $\left|\frac{1}{2}i \pm \frac{1}{2}\right|^2 = \sqrt{\left(\frac{1}{2}\right)^2 + \left(\frac{\pm 1}{2}\right)^2}^2 = \frac{1}{2}$

2. Bob's ground state is $\{\frac{1}{\sqrt{2}}\left(\ket{0} \pm i\ket{1}\right)\}$

   $$\left(\frac{1}{\sqrt{2}}\left(\ket{0} \pm i\ket{1}\right)\right)\left(\frac{1}{\sqrt{2}}\left(\bra{0} \pm i\bra{1}\right)\right)\left(\frac{1}{\sqrt{2}}(i\ket{0} + \ket{1})\right)\\ \,\\ = \left\{ \begin{array}{ll} \left(\frac{1}{2}i + \frac{1}{2}i = i\right)\frac{1}{\sqrt{2}}\left(\ket{0} + i\ket{1}\right) & \text{if}\; \frac{1}{\sqrt{2}}\left(\ket{0} + i\ket{1}\right) \\ \\ \left(\frac{1}{2}i - \frac{1}{2}i = 0\right)\frac{1}{\sqrt{2}}\left(\ket{0} - i\ket{1}\right) & \text{if}\; \frac{1}{\sqrt{2}}\left(\ket{0} - i\ket{1}\right) \end{array} \right.$$
   • So the probability that the result would be $\frac{1}{\sqrt{2}}\left(\ket{0} + i\ket{1}\right)$ is $|i|^2 = 1$, otherwise $|0|^2 = 0$

$X$ gate does not affect the result. That's the why it's not necessary to remove it.

In case Alice's request $a = 0$ then the result is well-known quantum state $\ket{\pm}$ but what are others? These states are rotated $\frac{\pi}{2}$ from $\ket{\pm}$.

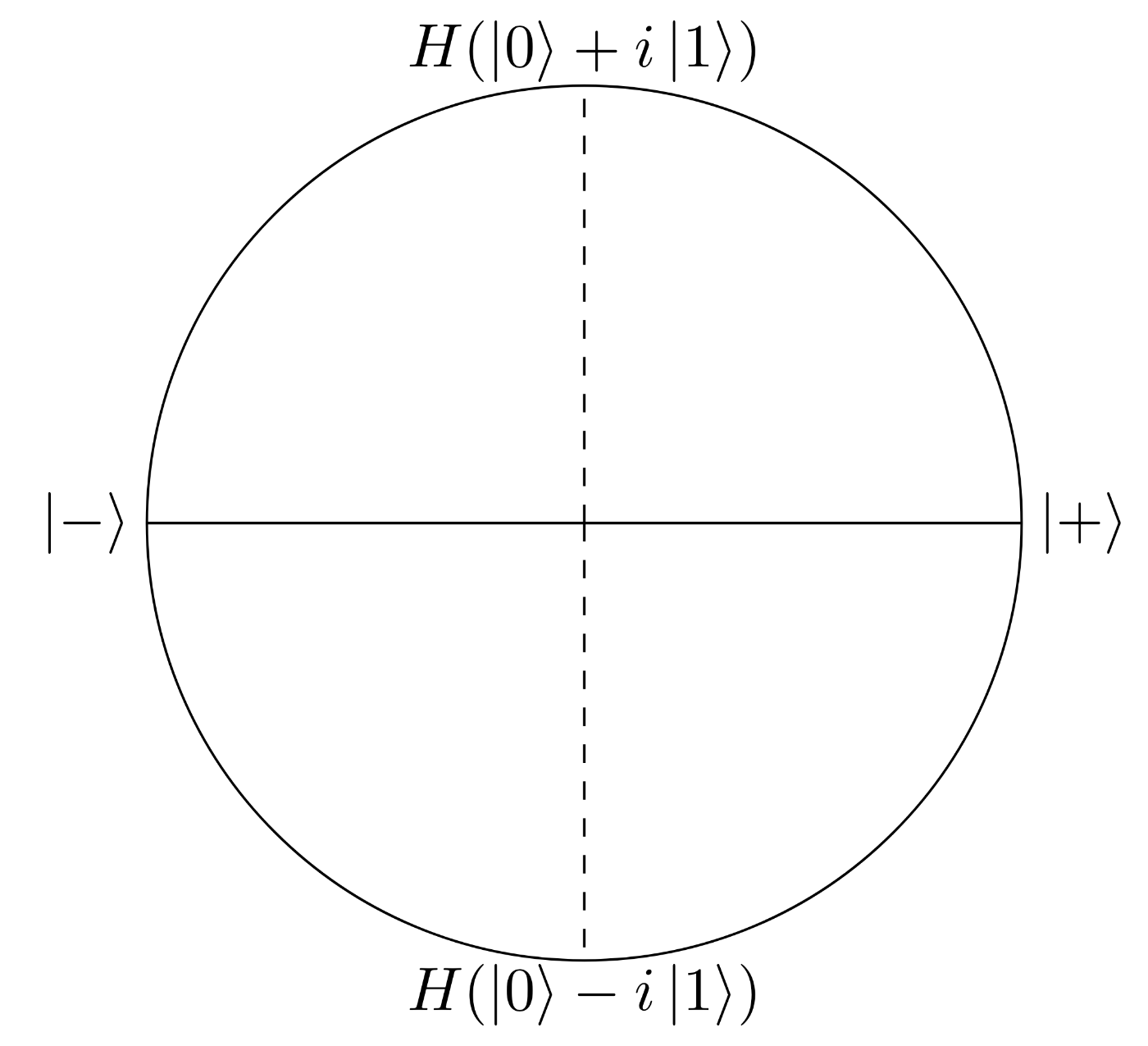
In procedure (6) Bob choose $\mathcal{B}_{\overline{b}}$, it means that Bob choose the dashed line or solid line of the above figure. If the their inputs are the same then the second qubit and the ground state are orthogonal so the result is a random value, on the other hand $z = x$.
Finally the result of this protocol is $a \oplus x \oplus z = a$ where $a \ne b \Rightarrow z = x$ so it's legal as the output of $\mathcal{F}$.

Random value $x$

In procedure (4), you maybe doubted whether a random value $x$ is actually needed or not. If $x$ would be gone, the following table shows all patterns of the second qubit.

$a$	$\delta$	$y$	Second qubit
$0$	$\theta$	$0$	$H\ket{0} = \ket{+}$
$0$	$\theta$	$1$	$XH\ket{0} = \ket{+}$
$1$	$\theta + \frac{\pi}{2}$	$0$	$H(\ket{0} + i\ket{1}$
$1$	$\theta + \frac{\pi}{2}$	$1$	$XH(\ket{0} + i\ket{1}$

The second qubit is either one of the red parts of the following figure.

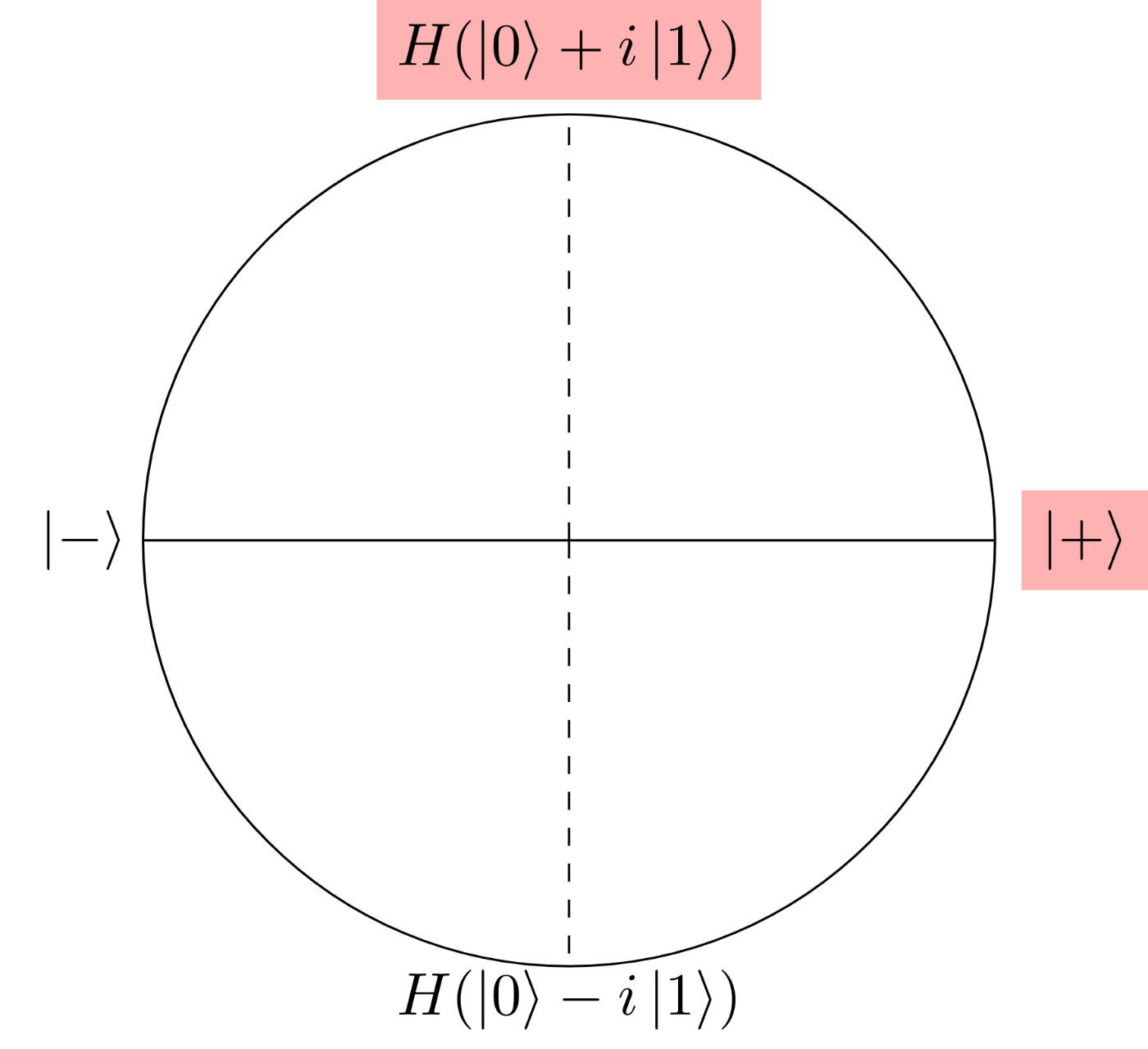
Similar to the naive protocol, if the result would be $\{\ket{-}, H(\ket{0} - i\ket{1})\}$ so Bob would measure $z = 1$ then Bob could know $a \ne b(\Rightarrow a = \overline{b})$ in procedure (7). So $x$ is required to avoid this information leakage.

Conclusion

I explained two quantum covert lottery protocols. In the original paper, the author extends two-party protocol to many-party. So I want to extend this quantum version protocol to many-party.

References

• 量子コンピュータで2人の“Covert”⁉️ガチャ (Japanese)
• Card-Based Covert Lottery
• 観測に基づく量子計算 (Japanese)
• 量子計算理論 量子コンピュータの原理 (Japanese)
• 量子コンピューティング: 基本アルゴリズムから量子機械学習まで (Japanese)

脚注

1. I call this article original paper in this article.

2. In this article I don't discuss about card-based cryptography so it's no problem not to know about it.

3. $\oplus$ means XOR operator.

4. $\otimes$ means tensor product.