量子コンピュータで2人の“Covert”⁉️ガチャ

English version is https://zenn.dev/yyu/articles/c45bb407e14594 .

はじめに

“Covert Lottery” とは論文Card-Based Covert Lottery^[1]で導入された用語である。これはプレイヤーの秘密の希望を入力し、

1. それらが衝突しないのであれば希望通りにし
2. そうでないなら、ランダムな結果を出力する

というプロトコルである。たとえば将棋などで2人のプレイヤーが先手・後手を決める場合に使うことができる。この2人のプレイヤーはそれぞれ先手・後手のどちらにしたいという希望があるものとするが、一方でこの希望を相手に明らかにしてしまうと、戦略が流出する可能性がある。したがってこのプレイヤー2人がCovert Lotteryを行えば、各々の希望が先手・後手の希望が噛み合った（衝突していない）時にはそれを出力し、一方で2人ともが先手・後手のいずれかを希望した場合はランダムに決定する。このようにすれば2人のプレイヤーは自分の入力した希望通りとなったのか、それとも衝突してランダムに決定されたのか知ることができないため、戦略が流出しない。
元論文ではこのようなプロトコルをカードベース暗号^[2]で構成しているが、筆者が軽く読んだ限りでは量子コイントスでも達成できそうであったため、この記事では量子コイントスでこれをどのように達成するかについて議論する。
この記事にもし何かの誤りがあったとしてもこの記事の筆者の落ち度であるので、コメントなどで気軽に教えてほしい。

2人のCovert Lotteryを行う関数

この節では元論文で説明されている2人のCovert Lottery（先手・後手を秘密に決定する）についてまず説明する。いま2人のプレイヤーとしてアリスとボブがいるものとする。アリスの入力を$a$として、アリスが先手を希望するならならば$a = 1$となり、後手を希望するなら$a = 0$となる。ボブについても同様に先手を希望するなら$b = 1$であり、後手を希望するなら$b = 0$とする。つまり先手なら$1$、後手なら$0$というエンコードになっている。
そして$\mathcal{F}$を「アリスの先手・後手を出力する関数」であるとすると、次のようになる。

$$\mathcal{F}(a, b) := \left\{ \begin{array}{lr} a & \text{if}\; a \ne b \\ i \xleftarrow{\text{rnd}} \{0, 1\} & \text{if}\; a = b \end{array} \right.$$

ただし$\xleftarrow{\text{rnd}} \{0, 1\}$は$\{0, 1\}$からランダムに片方を選ぶことを意味している^[3]。

議論の前に、この後すぐに使うので先に表記として$\overline{x}$を導入しておく。これは$x \in \{0,1\}$にNOT演算を適用した結果を意味している。たとえば$x = 0$であれば$\overline{x} = 1$となる。

さて、この関数$\mathcal{F}$について考える。今もし$a \ne b$であったとしたら、$a, b \in \{0, 1\}$であるから、$a = \overline{b}$となる。逆に$a = b$であれば$\{a, \overline{b}\} = \{0, 1\}$である。この2つをまとめると$\mathcal{F}$を次のように書き直せる。

$$\mathcal{F}(a, b) = \left\{ \begin{array}{lr} a\, (= \overline{b}) & \text{if}\; a \ne b \\ i \xleftarrow{\text{rnd}} \{a, \overline{b}\} & \text{if}\; a = b \end{array} \right.$$

ここで$a \ne b$のケースは実は$a = \overline{b}$なため、$\{a, \overline{b}\}$からどちらかを選んだ結果と等しくなる。そのためもはやこの場合分けは不要となり$\mathcal{F}$は次のようになる。

$$\mathcal{F}(a, b) = r \xleftarrow{\text{rnd}} \{a, \overline{b}\}$$

元論文では、$a, b$を秘密にしたままこのような関数$\mathcal{F}$をカードプロトコルで構成していた。その説明が気になる人は元論文を入手してもらうとして、ここでは量子コンピュータを利用した方法を紹介する。

BB84ベースの2人による量子Covert Lottery

それでは実際に量子コンピュータを利用したナイーブなプロトコルについて説明する^[4]。今、アリスとボブの2人が先手・後手を決めたいと考えている。前節と同様に$1$を先手、$0$を後手として次のようなプロトコルを実行する。

後に述べるようにこのプロトコルには脆弱性がある！

まずは簡単さを優先したプロトコルを紹介し、そのあとどのような問題があるかを見ていくことにする。

プロトコル

1. アリスは1bitの乱数$x \xleftarrow{\text{rnd}} \{0, 1\}$と、先手・後手の希望$a \in \{0, 1\}$を選択する

2. アリスは$a, x$を用いて次の4つ量子状態から1つ$\ket{\psi_{a,x}}$を選択する

   $$\def\bra#1{\mathinner{\left\langle{#1}\right|}} \def\ket#1{\mathinner{\left|{#1}\right\rangle}} \left\{ \begin{array}{lcl} \ket{\psi_{0,0}} & \equiv & \ket{0} \\ \ket{\psi_{0,1}} & \equiv & \ket{1} \\ \ket{\psi_{1,0}} & \equiv & \ket{+} \\ \ket{\psi_{1,1}} & \equiv & \ket{-} \end{array} \right.$$
   • ただし$\ket{\pm} \equiv \frac{1}{\sqrt{2}}\left(\ket{0} \pm \ket{1}\right)$とする

3. アリスはボブへ量子ビット$\ket{\psi_{a,x}}$を送信する

4. ボブは量子状態$\ket{\psi_{a,x}}$を受信し、ボブの希望$b \in \{0, 1\}$を選択する

5. ボブは次のような基底状態$\mathcal{B}_{\overline{b}}$で$\ket{\psi_{a,x}}$を測定し、測定結果を$y$とする

   $$\mathcal{B}_{\overline{b}} \equiv \left\{\ket{\psi_{\overline{b},0}}, \ket{\psi_{\overline{b},1}}\right\}$$
   • $\overline{b}$を利用することに注意する

6. ボブはアリスへ$y$を送信する

7. アリスは$y$を受けとり、$a \oplus x \oplus y$^[5]をボブへ送信しプロトコルの結果とする

このプロトコルだけ見せられても実際に正しく動作しているのかよく分からないと思うので、アリスの変数$a, x$とボブの変数$b$について$y$や$a \oplus x \oplus y$がどうなるのか？というのを次の表にまとめた。

$a$	$x$	$\ket{\psi_{a,x}}$	$\overline{b}$	$\mathcal{B}_{\overline{b}}$	$y$	$a \oplus x \oplus y$
$0$（後手）	$0$	$\ket{0}$	$0$（先手）	$\left\{\ket{0}, \ket{1}\right\}$	$0$	$0$
$0$（後手）	$0$	$\ket{0}$	$1$（後手）	$\left\{\ket{+}, \ket{-}\right\}$	$r \xleftarrow{\text{rnd}} \{0, 1\}$	$r \xleftarrow{\text{rnd}} \{0, 1\}$
$0$（後手）	$1$	$\ket{1}$	$0$（先手）	$\left\{\ket{0}, \ket{1}\right\}$	$1$	$0$
$0$（後手）	$1$	$\ket{1}$	$1$（後手）	$\left\{\ket{+}, \ket{-}\right\}$	$r \xleftarrow{\text{rnd}} \{0, 1\}$	$r \xleftarrow{\text{rnd}} \{0, 1\}$
$1$（先手）	$0$	$\ket{+}$	$0$（先手）	$\left\{\ket{0}, \ket{1}\right\}$	$r \xleftarrow{\text{rnd}} \{0, 1\}$	$r \xleftarrow{\text{rnd}} \{0, 1\}$
$1$（先手）	$0$	$\ket{+}$	$1$（後手）	$\left\{\ket{+}, \ket{-}\right\}$	$0$	$1$
$1$（先手）	$1$	$\ket{-}$	$0$（先手）	$\left\{\ket{0}, \ket{1}\right\}$	$r \xleftarrow{\text{rnd}} \{0, 1\}$	$r \xleftarrow{\text{rnd}} \{0, 1\}$
$1$（先手）	$1$	$\ket{-}$	$1$（後手）	$\left\{\ket{+}, \ket{-}\right\}$	$1$	$1$

このようにアリスとボブの先手・後手の希望が異なる時に限って最終的な出力$a \oplus x \oplus y$がアリスの先手・後手を示すようになっている。
なぜこのようになるのか？そのアイディアをまとめると

• $a = \overline{b}\,(\Rightarrow a \ne b)$のときは（5）の測定結果$y$はアリスの乱数$x$と必ず一致する
  • 一方で$a \ne \overline{b}$のときは$y$が乱数になるため、$a \oplus x \oplus y$は最終的に乱数とXORするので乱数となりOKである
• $a = \overline{b}$なときは$x = y$なので、したがって$a \oplus x \oplus y$のXORはキャンセルされて$a$が計算される

参加者の性質

このプロトコルでは（7）で最後にアリスの手元で行なわれる計算が最終的な結果となるため、アリスが不誠実であればここで結果を意図的に変更できる。したがってこれは少なくともアリスがセミオネスト^[6]であるという仮定の下でしか上手くいかない。

確率的な情報リーク

あらかじめ述べておいた脆弱性として、このプロトコルは確率でボブの情報（先手・後手の選択）がアリスへリークする。どういうことかを次のような具体的な例で考える。

1. アリスは$a = 0, x = 0$を選んだため、送信するのは$\ket{0}$となる
2. ここでもしボブが$\overline{b} = 1\,(\Rightarrow b = 0)$を選んだとする
3. このとき$\ket{0}$を$\left\{\ket{+}, \ket{-}\right\}$で測定するため、50%ずつの確率で$y = 0$または$y = 1$が発生する
   • ここでもし$y = 0$となった場合はアリスへの情報リークはない
4. 一方でもしここで$y = 1$が生じた場合、$\left\{\ket{0}, \ket{1}\right\}$で測定した場合には100%で$y = 0$なため、$\overline{b} = 1$であることがリークする

したがって、このプロトコルは最終的な結果は$\mathcal{F}$として問題ないが、アリスは確率的にボブの希望$b$を知ることができてしまい問題がある。

CZゲートと1量子ビットの測定型量子計算

先にプロトコルで利用する$CZ$ゲートと、Z軸に回転させた基底による測定について説明する。

CZゲート

$$CZ \equiv \ket{0}\bra{0}\otimes I + \ket{1}\bra{1}\otimes Z$$

ただし$I$と$Z$は次のような量子ゲートになる^[7]。

$$I \equiv \left(\begin{array}{cc} 1 & 0 \\ 0 & 1 \end{array}\right), \; Z \equiv \left(\begin{array}{cc} 1 & 0 \\ 0 & -1 \end{array}\right)$$

$CZ$ゲートは2量子ビットへの量子ゲートであり、次のような動作になる^[8]。

• 1番目の量子ビットの状態が$\ket{0}$であれば、2番目の量子ビットに何もしない
• 1番目の量子ビットの状態が$\ket{1}$であれば、2番目に$Z$量子ゲートを作用させる

今、例として$\ket{\chi} := a\ket{0} + b\ket{1}$と$\ket{+}$を$CZ$ゲートで結合したとすると、次のようになる。

$$\def\braket#1#2{\mathinner{\left\langle{#1}\middle|#2\right\rangle}} \begin{align*} CZ\ket{\chi}_1\ket{+}_2 &= \ket{0}\braket{0}{\chi}_1 I\ket{+}_2 + \ket{1}\braket{1}{\chi}_1 Z\ket{+}_2 \\ &= \ket{0}\braket{0}{\chi}_1 \ket{+}_2 + \ket{1}\braket{1}{\chi}_1 \ket{-}_2 \\ &= a\ket{0}_1\ket{+}_2 + b\ket{1}_1\ket{-}_2 \end{align*}$$

ここで、各量子ビットについている$1,2$の添字はそれぞれ1番目の量子ビット、2番目の量子ビットを意味する。

1量子ビットの測定型量子計算

さらに、この$CZ$ゲートを適用した$CZ\ket{\chi}_1\ket{+}_2$の射影測定について考える。普通の測定では$\left\{\ket{0}, \ket{1}\right\}$を利用するが、ここでは適当な角度$\phi$を用いた$\left\{\ket{0} \pm e^{i\phi}\ket{1}\right\}$を利用する。
今1量子ビット目にある$\ket{\chi}_1$を測定し、$\ket{0} + e^{i\phi}\ket{1}$得られたとすると、2番目の量子ビットは次のようになる。

$$(\ket{0}_1 + e^{i\phi}\ket{1}_1)(\bra{0}_1 + e^{i\phi}\bra{1}_1) \cdot (a\ket{0}_1\ket{+}_2 + b\ket{1}_1\ket{-}_2) = (\ket{0}_1 + e^{i\phi}\ket{1}_1)(a\ket{+}_2 + be^{i\phi}\ket{-}_2)$$

この$a\ket{+}_2 + be^{i\phi}\ket{-}_2$はさらに次のように変形できる。

$$\begin{align*} a\ket{+}_2 + be^{i\phi}\ket{-}_2 &= \frac{1}{\sqrt{2}}\left(a\ket{0} + a\ket{1} + be^{i\phi}\ket{0} - be^{i\phi}\ket{1}\right) \\ &= \frac{1}{\sqrt{2}}\left((a + be^{i\phi})\ket{0} + (a - be^{i\phi})\ket{1}\right) \end{align*}$$

これはアダマールゲート$H$と位相ゲート$R_Z$^[9]を利用して最終的に次のようになる。

$$\frac{1}{\sqrt{2}}\left((a + be^{i\phi})\ket{0} + (a - be^{i\phi})\ket{1}\right) = HR_Z(\phi)\ket{\chi}$$

もし射影測定で直交する$\ket{0} - e^{i\phi}\ket{1}$が観測された場合は量子的なNOTである$X$ゲートによって次のように表現できる。

$$XHR_Z(\phi)\ket{\chi}$$

なおアダマールゲート$H$、位相ゲート$R_Z$そして$X$はそれぞれ次のようになる。

$$H \equiv \frac{1}{\sqrt{2}}\left(\begin{array}{cc} 1 & 1 \\ 1 & -1 \end{array}\right), \; R_Z(x) \equiv \left(\begin{array}{cc} 1 & 0 \\ 0 & e^{ix} \end{array}\right), \; X \equiv \left(\begin{array}{cc} 0 & 1 \\ 1 & 0 \end{array}\right)$$

この一連の操作で生じたことというのは、1番目の量子ビット$\ket{\chi}$が$CZ$ゲートで連結された2番目の量子ビット$\ket{+}$へ移動（テレポート）し、かつ角度$\phi$を埋め込んだ基底を測定に利用することで、$\ket{\chi}$にアダマールゲートと位相ゲートを作用させた状態となった。場合によっては$X$ゲートが入ってしまうが、それは1番目の量子ビットを測定した観測結果によって$X$ゲートが生じたかどうか？が明らかなので問題はない。

2人のブラインド量子Covert Lottery

ここからはやや複雑な方法に挑戦する。先にアイディアを述べると、これはブラインド量子計算^[10]のような方法で、前節では古典的に行なっていたXORのような操作を量子2量子ビットのもつれで行うようなイメージである。

プロトコル

1. アリスはランダムな角度$\theta \xleftarrow{\text{rnd}} \left\{0, \frac{1\pi}{4}, \dots, \frac{7\pi}{4}\right\}$を選ぶ

2. アリスは次のような1量子ビット$\ket{+_\theta}$を作成しボブへ送信する

   $$\ket{+_\theta} \equiv \frac{1}{\sqrt{2}}\left(\ket{0} + e^{-i\theta}\ket{1}\right)$$

3. ボブはアリスから受けとった$\ket{+_\theta}$と$\ket{+}$を次のような$CZ$ゲートで結合する

   $$CZ\ket{+_\theta}_1\ket{+}_2$$

   • $CZ\ket{+_\theta}_1\ket{+}_2$は次のように整理できる

     $$CZ\ket{+_\theta}_1\ket{+}_2 = \frac{1}{\sqrt{2}}\ket{0}_1\ket{+}_2 + \frac{e^{-i\theta}}{\sqrt{2}}\ket{1}_1\ket{-}_2$$

4. アリスは希望$a \in {0, 1}$と乱数$x \xleftarrow{\text{rnd}} \{0, 1\}$を選び、それに基づいて次のような角度$\delta$を選びボブへ送信する

   $$\delta := \left\{ \begin{array}{ll} \theta + x\pi& \text{if}\; a = 0 \\ \theta + \frac{\pi}{2} + x\pi & \text{if}\; a = 1 \end{array} \right.$$

5. ボブは受けとった$\delta$から次のような基底$\left\{\ket{0} \pm e^{i\delta}\ket{1}\right\}$を用意して1番目の量子ビットを測定し、その結果を$y \in \{0, 1\}$とする

6. ボブは希望$b \in \{0, 1\}$を選び、それによって次から基底$\mathcal{B}_{\overline{b}}$を作成する

   $$\left\{ \begin{array}{lcl} \mathcal{B}_{0} & \equiv & \left\{\ket{\pm}\right\} \\ \mathcal{B}_{1} & \equiv & \left\{\frac{1}{\sqrt{2}}\left(\ket{0} \pm i\ket{1}\right)\right\} \end{array} \right.$$

7. ボブは2番目の量子ビットを$\mathcal{B}_{\overline{b}}$で測定して結果を$z$として、$z$をアリスへ送信する

8. アリスはプロトコルの出力として$a \oplus x \oplus z$を得る

動作の解説

手順（5）の測定がややこしい。$CZ$ゲートの節を参考にすると、1番目の量子ビットを基底$\left\{\ket{0} \pm e^{i\delta}\ket{1}\right\}$で測定した後の2番目の量子ビットは次のようになる。

1. $y = 0$のとき

   $$\begin{align*} HR_Z(\delta)\ket{+_\theta} &= H\left(\ket{0} + e^{-i\theta}\cdot e^{i\delta}\ket{1}\right) \\ &= H\left(\ket{0} + e^{i(\delta - \theta)}\ket{1}\right) \end{align*}$$

2. $y = 1$のとき

   $$XHR_Z(\delta)\ket{+_\theta} = XH\left(\ket{0} + e^{i(\delta - \theta)}\ket{1}\right)$$

したがって$\delta - \theta$の結果によって2番目の量子ビットがどのようになるかが決定される。ここでアリスの選択に応じて2番目の量子ビットがどのように変化するのかを次の表にまとめた。

$a$	$x$	$\delta$	$y$	2番目の量子ビット
$0$（後手）	$0$	$\theta$	$0$	$H\ket{0} = \ket{+}$
$0$（後手）	$0$	$\theta$	$1$	$XH\ket{0} = \ket{+}$
$0$（後手）	$1$	$\theta + \pi$	$0$	$H\ket{1} = \ket{-}$
$0$（後手）	$1$	$\theta + \pi$	$1$	$XH\ket{1} = \ket{-}$
$1$（先手）	$0$	$\theta + \frac{\pi}{2}$	$0$	$H(\ket{0} + i\ket{1}$
$1$（先手）	$0$	$\theta + \frac{\pi}{2}$	$1$	$XH(\ket{0} + i\ket{1}$
$1$（先手）	$1$	$\theta + \frac{\pi}{2} + \pi$	$0$	$H(\ket{0} - i\ket{1})$
$1$（先手）	$1$	$\theta + \frac{\pi}{2} + \pi$	$1$	$XH(\ket{0} - i\ket{1})$

このように$y = 1$な場合は$X$ゲートが生じてしまう。$X$ゲートで相殺する必要を感じるかもしれないが、実はこれは放置しておいてよい。たとえば2番目の量子ビットが$XH(\ket{0} + i\ket{1}) = \frac{1}{\sqrt{2}}\left(i\ket{0} + \ket{1}\right)$となっているとする。そして手順（6）でボブが測定に利用する基底が2種類あるので、その2つに場合分けして考える。

1. ボブの基底が$\{\ket{\pm}\}$のとき

   $$\ket{\pm}\bra{\pm}\left(\frac{1}{\sqrt{2}}(i\ket{0} + \ket{1})\right) = \left(\frac{1}{2}i \pm \frac{1}{2}\right)\ket{\pm}$$
   • したがって$\ket{\pm}$となる確率はいずれも$\left|\frac{1}{2}i \pm \frac{1}{2}\right|^2 = \sqrt{\left(\frac{1}{2}\right)^2 + \left(\frac{\pm 1}{2}\right)^2}^2 = \frac{1}{2}$

2. ボブの基底が$\{\frac{1}{\sqrt{2}}\left(\ket{0} \pm i\ket{1}\right)\}$のとき

   $$\left(\frac{1}{\sqrt{2}}\left(\ket{0} \pm i\ket{1}\right)\right)\left(\frac{1}{\sqrt{2}}\left(\bra{0} \pm i\bra{1}\right)\right)\left(\frac{1}{\sqrt{2}}(i\ket{0} + \ket{1})\right)\\ \,\\ = \left\{ \begin{array}{ll} \left(\frac{1}{2}i + \frac{1}{2}i = i\right)\frac{1}{\sqrt{2}}\left(\ket{0} + i\ket{1}\right) & \text{if}\; \frac{1}{\sqrt{2}}\left(\ket{0} + i\ket{1}\right) \\ \\ \left(\frac{1}{2}i - \frac{1}{2}i = 0\right)\frac{1}{\sqrt{2}}\left(\ket{0} - i\ket{1}\right) & \text{if}\; \frac{1}{\sqrt{2}}\left(\ket{0} - i\ket{1}\right) \end{array} \right.$$
   • したがって$\frac{1}{\sqrt{2}}\left(\ket{0} + i\ket{1}\right)$が観測される確率は$|i|^2 = 1$であり、一方で$\frac{1}{\sqrt{2}}\left(\ket{0} - i\ket{1}\right)$が観測される確率は$|0|^2 = 0$となる

したがって、$X$ゲートの存在はこのプロトコルにおいて最終的なアウトプットに影響しないため、とくに打ち消すような処理はしなくてもよい。

さて、アリスが後手を選んだ状態はよく知られた状態$\ket{+}, \ket{-}$となっているが、一方で残った2つはどういう状態かが問題となる。この状態は$\delta$に$\frac{\pi}{2} = 90^\circ$が加算されているため、$\ket{+}, \ket{-}$から丁度$\frac{\pi}{2}$ずらした破線のところである。

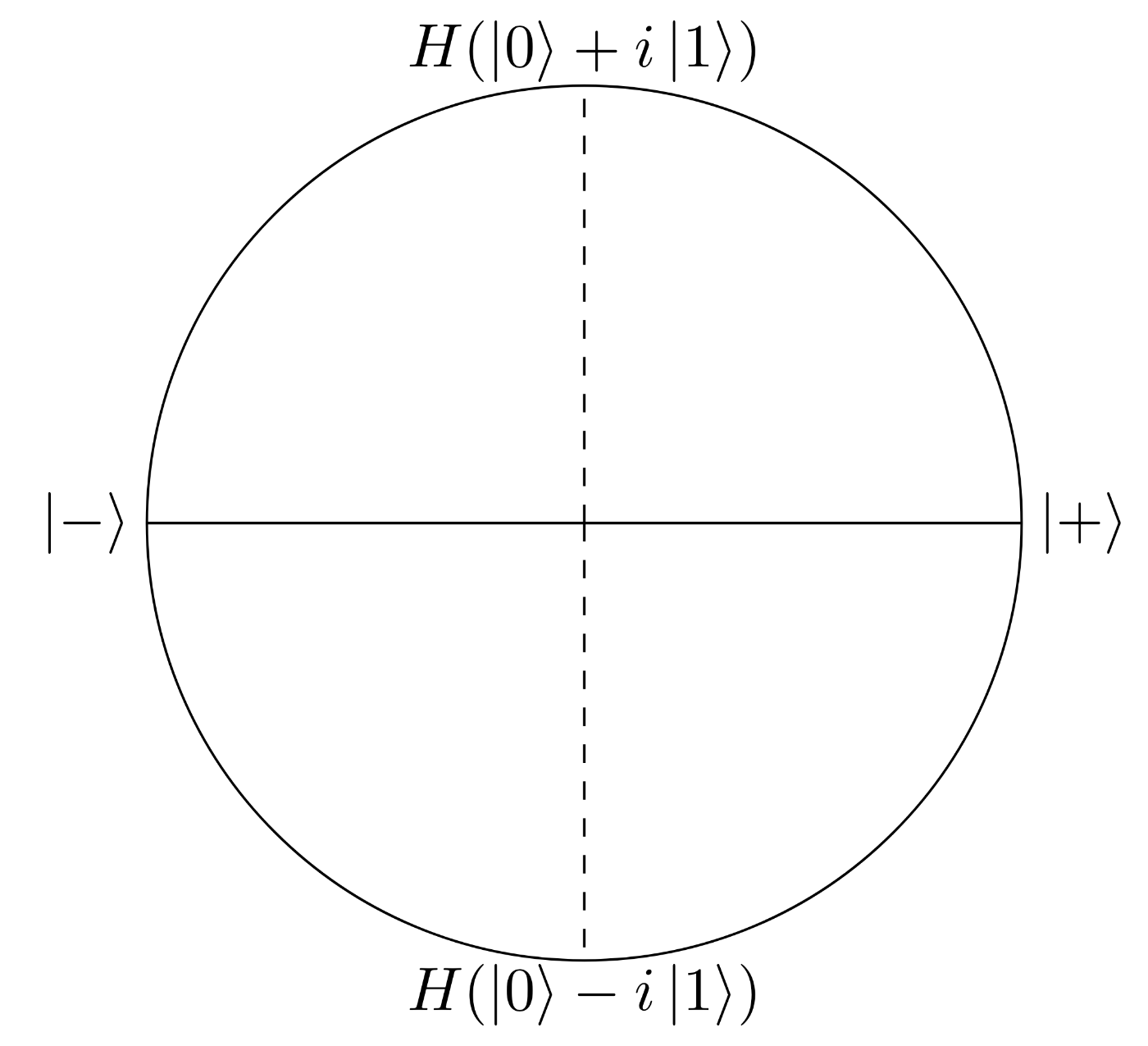
ブロッホ球のZ軸から見た時の位置関係

このあとボブは手順（6）で基底$\mathcal{B}_{\overline{b}}$を選ぶが、$H(\ket{0} \pm i\ket{1}) = \frac{1}{\sqrt{2}}\left(\ket{0} \pm i\ket{1}\right)$なのでボブの希望$b$によって上図の実線にあたる$\{\ket{\pm}\}$が基底となるか、それとも破線にあたる$\{\frac{1}{\sqrt{2}}\left(\ket{0} \pm i\ket{1}\right)\}$が基底となるかが決定する。アリスとボブの選択が等しいとき（$a = b$）は2番目の量子ビットがと基底が$\frac{\pi}{2}$ずれているため結果はランダムになり、そうでないときは$z = x$となる。
そして手順（8）の最終的な結果は、$a \ne b$の場合は常に$z = x$となるため、このときに限っては確実に$a \oplus x \oplus z = a$となり、$\mathcal{F}$の出力として妥当となる。

アリスの乱数$x$

プロトコルの手順（4）では、なぜアリスが乱数$x$を必要とするのかということが気になったかもしれない。もしここで$x$がなかったとしたら、2番目の量子ビットは次の表のようになる。

$a$	$\delta$	$y$	2番目の量子ビット
$0$（後手）	$\theta$	$0$	$H\ket{0} = \ket{+}$
$0$（後手）	$\theta$	$1$	$XH\ket{0} = \ket{+}$
$1$（後手）	$\theta + \frac{\pi}{2}$	$0$	$H(\ket{0} + i\ket{1}$
$1$（後手）	$\theta + \frac{\pi}{2}$	$1$	$XH(\ket{0} + i\ket{1}$

これはブロッホ球では次の図の赤い部分のどちらかとなる。

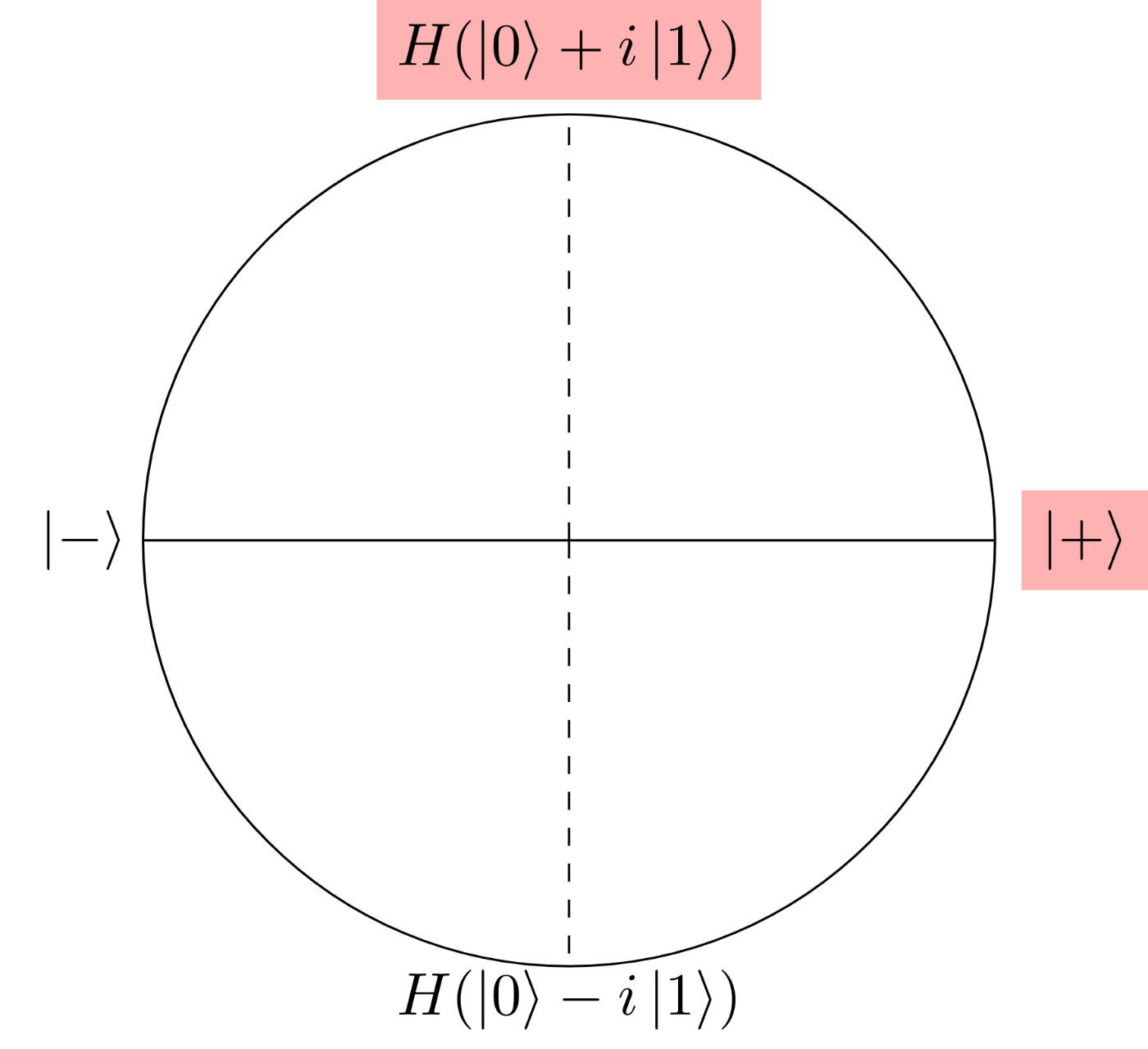
つまり、ナイーブなプロトコルで説明したように$\{\ket{-}, H(\ket{0} - i\ket{1})\}$のいずれか、つまり手順（7）でボブが$z = 1$を観測してしまったときに、ボブは$a \ne b(\Rightarrow a = \overline{b})$であると確信する。つまりアリスの希望$a$が確率で流出することとなる。これを避けるために、アリスは乱数$x$を使うことで$z = 1$が生じたのが

• ボブとアリスの選択肢が不一致であったためか
• それとも選択肢は一致していたが、乱数$x = 1$によるものか

という上記2つの区別がボブにとってつかないようにする。

Covert Lotteryとガチャ

元論文でもCovert Lotteryと呼ばれているように、これは先手・後手の決定とは別にくじに使うことができる。元論文ではこの2人のCovert Lotteryを任意の多人数へ拡張して次のような説明をしている。

• $n$人の$P_1, \dots P_n$参加者が$m$個の景品$I_1, \dots, I_m$のうちいくつか（0個もOK）が欲しいと考えている
• 景品$I_i$について、プレイヤーは$0$または$1$を投票する
• このとき
  1. もし1人のプレイヤー$P_j$のみが$1$を投票し、それ以外の全プレイヤーが$0$を投票していれば$P_j$が景品$I_i$を入手する
  2. 一方で複数のプレイヤーが$1$を投票した場合は、そのプレイヤーの中からランダムに1人を決定する

つまり、2人のCovert Lotteryも上記のように考えると、2人のプレイヤーにおいて次のようになる。

• どちらか1人のみ景品が欲しい場合はそちらに景品が当選する
• 2人ともが景品が欲しい・欲くない場合はランダムに当選者が選択される

つまり複数のプレイヤー間で、プレイヤーの希望を隠蔽したまま景品をなるべく希望に沿う形で当選させることができる。たとえば欲しくない景品が当選したので転売するといったことはあるだろうと思うので、そういったことをなるべく少なくできるかもしれない。

まとめ

アリスがセミオネストであるという仮定をなんとか取り除けないか多少は考えたものの、すぐには思いつかなかったのでいったんこのままで公開することにした。もしよい方法を思いついたという方がいれば教えてほしい。
また元論文では今回紹介した2人のプロトコルを任意の人数へ拡張していたため、そちらも量子プロトコルで達成できないか？というのを考えてみたい。

参考文献

• Card-Based Covert Lottery
  • PDF
• 観測に基づく量子計算
• 量子計算理論 量子コンピュータの原理
• 量子コンピューティング: 基本アルゴリズムから量子機械学習まで

脚注

1. この論文のことを今後は「元論文」という呼ぶことにする。

2. この文書を読むうえではカードベース暗号の知識は必要ないが、これはこれで非常におもしろいので、たとえばカード組を用いた秘密計算といった文献を読むとよい。

3. 元論文では矢印の上に$（LaTeX表記では\xleftarrow{\text{$}}）の記号を利用してランダムを表現しているが、Zennのパーザーの都合（？）でこの表記が数式として認められなかったため表記を変更した。

4. この記事では量子コンピュータの基本的な演算の知識を前提としている。このあたりは拙著の量子コンピュータを利用した公平なガチャ#古典計算機と量子コンピュータなどを参考にしてほしい。

5. $\oplus$はXOR演算を表す。

6. プレイヤーが「セミオネスト（semi-honest）」であるとき、このプレイヤーはプロトコルの指示には違反しないが、プロトコルの指示に従う限りで（できるなら）他プレイヤーの情報を奪うといった不誠実な振る舞いをする。

7. 記号$\otimes$はテンソル積を表す。

8. $CZ$ゲートは1番目・2番目の量子ビットを入れかえても量子的な効果に違いはない。これは数式で言うと$\ket{0}\bra{0}\otimes I + \ket{1}\bra{1}\otimes Z = I \otimes \ket{0}\bra{0} + Z \otimes \ket{1}\bra{1}$となることを意味する。したがって実際にはこの説明で1番目や2番目などと区別する必要性はないが、順番を明瞭にしないまま説明するのも不要な混乱を与えると考えてここでは順番を明示した。

9. この位相ゲートはブロッホ球における$Z$軸回転を表すためこのような表記とした。

10. ブラインド量子計算はセキュアクラウド量子計算とも呼ばれ、実際の計算内容や入力を秘密にしたまま量子計算を代行してもらう技術である。ブラインド量子計算について得に知らなくてもこの文書は読めるように書いたつもりだが、詳細が気になる方は観測に基づく量子計算といった本がおすすめできる。