概要
関数型プログラミングをやっているとlensという概念が出てくる。このlensがじつに多様な具体例を孕んでいることを知り面白く思った。この記事はその備忘録である。
Lensとは
そもそもlensとは、
f: S\rightarrow A,\quad g: S\times B \rightarrow T
なる関数の組(f,g)のことである。次のような図式で表すのが一般的である。
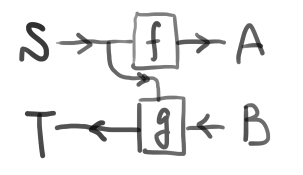
lensは次のように結合できることが重要である。
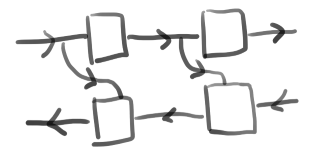
例1:GetterとSetter
lensの最も原初的な例はオブジェクトのGetterとSetterである。いまS\simeq T, A\simeq Bとする。またAのデータのみを持つオブジェクトをSとする。すると下図のとおり、fとgはそれぞれgetterとsetterになっていることがわかる。
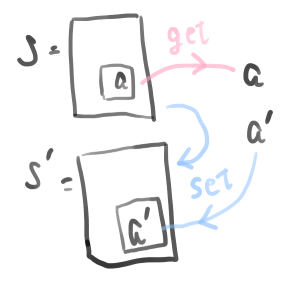
lensの合成はネストされたオブジェクトへのアクセスを表す。
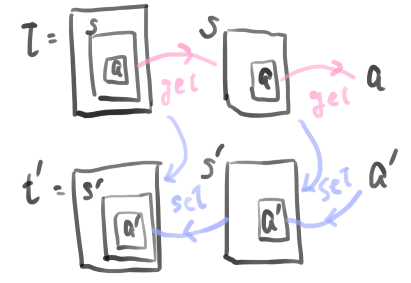
なお、S\times B \rightarrow Sなる関数はカリー化によってS\rightarrow S^Bとみなせる。そこでgetterとsetterをまとめて(f,g):S\rightarrow A\times S^Bなる関数だとすると、この関数(f,g)は函手TS=A\times S^Bに対する余代数を与える。さらにいえば、この形は有限オートマトンの型になっている。このことについては後で顧みる。
例2:余接ベクトル空間
ある空間Mとその上の一点p\in Mについて、p上の接ベクトル空間T_pMが定まる。点pを座標(x^1,x^2,...,x^n)で表すと、接ベクトルは\partial/\partial x^iを基底として
v = v^1 \frac{\partial}{\partial x^1} + v^2 \frac{\partial}{\partial x^2} + \cdots + v^n \frac{\partial}{\partial x^n}
などと表される。また接ベクトルの双対ベクトルを余接ベクトルと呼ぶ。余接ベクトルは\mathrm d x^iを基底として
v = v_1\mathrm d x^1 + v_2\mathrm d x^2 + \cdots + v_n\mathrm d x^n
などと展開される。p上の余接ベクトル空間をT_p^*Mと書く。
いまある空間Mから別の空間Nへの写像f:M\rightarrow Nへの写像を考える。対応するf(p)の座標を(y^1,y^2,...,y^m)とすると、変換は
y^k = f^k(x^1,x^2,...,x^n)\quad (k=1,2,...,m)
と表される。すると余接ベクトル空間の変換 f^*_p: T^*_{f(p)}N\rightarrow T^*_pMが定まり、それは
f^*(\mathrm d y^k) = \sum \frac{\partial f^k}{\partial x^i}(x^1,x^2,...,x^n) \mathrm dx^i
で与えられる。以上のことを図で表すと次のようになる。なおここでは右向きの矢印を下側に書いている。
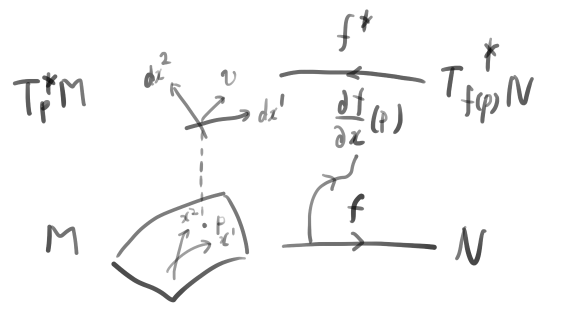
すなわち、変換(f,f^*)の組はlensになっている。lensの結合はそのまま写像の結合である。
ところで、ベクトルv\in T_p^*Mに対し、基底(\mathrm d x^1,\mathrm d x^2,...,\mathrm d x^n)を定めると成分表示(v_1,v_2,...,v_n)\in K_{(p)}^{\otimes n}が定まる。Kは実数\mathbb Rなどである。いま対応する点を添え字(p)で表しているが本来は不要である。変換f:M\rightarrow Nに対しf^*:T_{f(p)}^*N \rightarrow T^*_pMが定まるが、成分の空間ではさらに反転してK^{\otimes n}_{(p)}\rightarrow K^{\otimes m}_{\left(f(p)\right)}となる。そこで余接ベクトルの成分は共変ベクトルと呼ばれる。一方で接ベクトルの成分は反変ベクトルと呼ばれる。
なお、座標(x^1,x^2,...,x^n)が実数\mathbb R^nなら接ベクトルの成分も実数\mathbb R^nである。するとf^*の型は座標表示において\mathbb R^m \times \mathbb R^n \rightarrow \mathbb R^nとなる。何でも実数\mathbb R^nとなってしまうとどれがどれだったかじつに分かりにくいため、多様体論的な出自の違いを明記した方が分かりやすいように思われる。
例3:ニューラルネットワーク
3つ目の例はニューラルネットワーク、あるいはその一般化としての微分可能プログラミングである。だがそのエッセンスはすでに述べた余接ベクトル空間の例で尽きている。すなわちfが推論過程に対応し、f^*が逆誤差伝搬(後進自動微分)に対応する。実際はfがパラメータを持っているため、パラメトリックlensを考える必要がある。解説や実装は記事が詳しい。
ここで、自動微分という語はf:M\rightarrow Nからf^*: T^*N \rightarrow T^*Mを形式的に導出できることを意味している。したがって、微分(derivative)に関わらず、自動で導出(derivation)でき、lensとなるものであればアナロジーの展開は容易である。この方面での一般化はなにか有用なものがありそうに思われる。
例4:状態空間
最後の例は状態空間である。状態空間方程式は次で与えられるものである。
\left\{
\begin{split}
x_{n+1} &= g(x_n,u_n) \\
y_n &= f(x_n)
\end{split}
\right.
ここでx_nは現在の状態、x_{n+1}は1ステップ先の状態を表す。uは入力であり、yは出力、ないしは観測量と呼ばれる。この式はlensの定義式f: S\rightarrow A, g: S\times B \rightarrow Tをただ単純に書き下したものになっている。すなわちx_{n}\in S, y_n \in A, u_n\in B, x_{n+1} \in Tである。さきほど例1で有限オートマトンが登場したわけはここで明らかになる。lensは状態遷移系の構造を自然に与えており、その振る舞いを定義するには余代数を経る必要があったのである。
lens の合成は出力から入力をフィードバックすることを意味している。たとえばPID制御は次のように書くことができる。
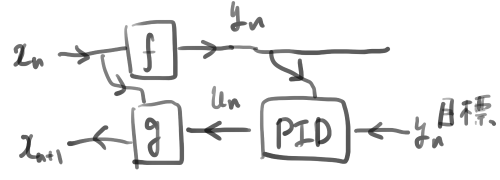
もっと興味深いのは脳の自由エネルギー原理によるフィードバックである。本では運動制御のモデルが紹介されている。そこでは状態を世界の心的モデル、観測量を脳への感覚入力とみなし、自由エネルギー原理に基づいて次なる行動が世界モデルを更新する入力として与えられている。lensの結合は心、脳、身体、環境といった内包構造をモデル化しているのである。
こうした脳や身体および環境の相互作用の考え方のオリジンはノーバート・ウィーナーによるサイバネティクスに他ならない。このような観点はストラスクライド大学の人たちが圏論的サイバネティクスというコンセプトで強化学習との関係などをいろいろ模索しているようである。
まとめ
lensはマトリョーシカのように入れ子となった構造に穴を開けてのぞき込むためのじつに普遍的な概念であることが分かった。






Discussion