余代数な有限機械のHaskell実装

概要

この記事は Bart Jacobs による "Introduction to Coalgebra" という大変面白い本の一部を Haskell で実装し確認したメモである。余代数や終余代数の概念をHaskell での実装を弾幕としてできるだけさりげなく導入する。またその適用例としてStream と有限オートマトンを構成する。結果として余代数が時間発展の構造(structure)を与えるとき、終余代数はその振る舞い(behaviour)を与えることを見る。また余帰納的（余再帰的）定義ということについても補足する。圏論の語彙は本質的な理解には差し替えないと思われる範囲で未定義のまま用いている。

Stream と余代数

Stream

有限オートマトンを扱う前に Stream でウォーミングアップする。Stream とはある型の値の無限個数の列である。いま Pair Functor を次のように定義してみよう。

data Pair a b = Pair a b

instance Functor (Pair a) where
    fmap f (Pair a b) = Pair a (f b)

すると Stream は擬コードで

Stream a = Pair a (Pair a (Pair a ( ... )))

と定義することができる。型 a を $A$ とし、 Pair a b を $A\times B$ と書くことにすれば Stream a は $A^\infty = A\times A\times \dots$ と書ける。型 a の値を無限個数保持するデータ型であることが Pair を用いて表現されている。

上の擬コードは次のように書き換えられる。

Stream a = Pair a (Stream a)

いまこの書き換えは

$$\begin{split} A^\infty &= A \times A \times A \times \cdots \\ &= A \times \left(A \times A \times A\times\cdots\right) \\ &= A \times A^\infty \end{split}$$

としたことに対応する。すなわち、Stream a $A^\infty$ とは
Pair a なる Functor $P_A(-) = A\times (-)$ の不動点である、すなわち $A^\infty=P_A(A^\infty)$ である、といえる。

そのような不動点は Data.Fix を用いて構成できる。

import Data.Fix
type Stream a = Fix (Pair a)

このままでは結果確認が不便なのでStream a をリスト[a]に変換するユーティリティを定義しておく。

toList :: Stream a -> [a]
toList = foldFix (elimPair [] (:)) 
  where 
    elimPair x f (Pair a b) = f a b

foldFix については補足で説明する。なおここでこの写像が全射でないことは留意すべき点である。実際、空リスト[] へ写像される点は存在しない。

余代数

さて、余代数である。いま状態 $S$ の$f$ による遷移と $g$ による出力

$$S \overset{f}{\longrightarrow} S, \quad S \overset{g}{\longrightarrow} A$$

を考えたい。ひとまとめにすると

$$S \overset{\langle f,g\rangle}{\longrightarrow} A\times S \simeq P_A(S)$$

である。一般に自己函手 $F$ に対して

$$A \overset{c}{\longrightarrow} F(A)$$

なる射 $c$ を $F$-余代数（$F$-coalgebra）と呼ぶ。その逆

$$F(A) \overset{a}{\longrightarrow} A$$

は$F$-代数($F$-algebra)なわけだが、$P_A$の場合で考えると

$$P_A(A) \simeq A\times A \overset{a}{\longrightarrow} A$$

であり、$A\times A \rightarrow A$ は $(a_0,a_1) \mapsto a_2= a_0 \star a_1$ なる二項間のなにかしらの代数演算に他ならない。したがって$F$-代数は我々になじみ深い代数計算の一般化であり、$F$-余代数はその双対というわけである。$c=\langle f,g\rangle$として、余代数の一つの例

$$S \overset{c}{\longrightarrow} A\times S$$

は

c :: (s -> s) -> (s -> a) -> s -> Pair a s
c f g n = Pair (g n) (f n)

と実装できる。

終余代数

ここでは定義や定理による構成を割愛し結果論的に終余代数を導入する。

$F$-余代数に対し$F$が不動点、すなわち

$$F(\mathrm{Fix}\,F) \simeq \mathrm{Fix}\,F$$

なる $\mathrm{Fix}\,F$ を持つとき、同型

$$\ \mathrm{Fix}\,F \rightarrow F(\mathrm{Fix}\,F)$$

を$F$余代数の終余代数と呼ぶ。終余代数が存在すると任意の$F$-余代数 $c:A\rightarrow F(A)$ に対して次の図式が可換になる。

$$\begin{array}{ccc} A & \overset{b}{\longrightarrow} & \mathrm{Fix}\,F \cr \downarrow &&\downarrow \cr F(A) & \longrightarrow & F(\mathrm{Fix}\,F) \end{array}$$

なお、任意の $A$ に対して

$$A\overset{!}{\longrightarrow} 1$$

なる唯一の射が存在するとする（終対象 1 が存在するとする）。すると$\mathrm{Fix}\,F$ は

$$\cdots \overset{F^3!}{\longrightarrow} F^31 \overset{F^2!}{\longrightarrow} F^21 \overset{F!}{\longrightarrow} F1 \overset{!}{\longrightarrow} 1$$

なる列の極限 $F^\infty 1$ として表せる（Adámekの定理）。$F(F^\infty 1) = F^{\infty+1}1 = F^\infty1$ というわけである。これは Stream a が$\mathrm{Fix}\,P_A$ でありかつ$A^\infty$ であることと整合している。実際にFix は

newtype Fix f = Fix { unFix :: f (Fix f) }

で定義されており、Fix f = f (Fix f) = f (f (Fix f)) =... である。

いま具体的に $b:A\rightarrow \mathrm{Fix}\,F$ を構成してみよう。函手 $P_A$ の不動点は $A^\infty$ すなわち Stream a であった。したがって $b:A\rightarrow \mathrm{Fix}\,F$ を構成するには a -> Stream a ができればよい。いま

stream :: (a -> a) -> a -> Stream a
stream g = unfoldFix (c g id)

としよう。ここでunfoldFixは型

unfoldFix :: Functor f => (a -> f a) -> a -> Fix f

を持ち、anamorphism とも呼ばれる。stream g が求める関数a -> Stream aとなる。いま f は Pair a であり Stream a は Fix (Pair a) であった。

ここで例題として コラッツ問題 の関数

collatz :: Int -> Int
collatz n 
    | even n = div n 2
    | otherwise = 3 * n + 1

を使ってみよう。実際に実行してみると

ghci> toList $ stream collatz 42
[42,21,64,32,16,8,4,2,1,4,2,1,4,2,1,...

となり、正しく計算できていることが分かる。これは Stream をリストに変換しているため無限リストになる。もっと穏便な実行方法は例えば

ghci> takeWhile (1 /=) $ toList $ stream collatz 27
[27,82,41,124,62,31,94,47,142,71,214,107,322,161,484,242,121,364,182,91,274,137,412,206,103,310,155,466,233,700,350,175,526,263,790,395,1186,593,1780,890,445,1336,668,334,167,502,251,754,377,1132,566,283,850,425,1276,638,319,958,479,1438,719,2158,1079,3238,1619,4858,2429,7288,3644,1822,911,2734,1367,4102,2051,6154,3077,9232,4616,2308,1154,577,1732,866,433,1300,650,325,976,488,244,122,61,184,92,46,23,70,35,106,53,160,80,40,20,10,5,16,8,4,2]

である。ここから分かるように、終余代数は余代数の振る舞い(behaviour) を与えており、また余代数は終余代数の構造(structure) を与えている。ここでの余代数は終余代数を除いている。また、この振る舞いは「余代数から余帰納的に定義された」と表現できる。実際、Stream型と stream関数の定義は最大不動点演算子 Nuを用いて

type Stream a = Nu (Pair a)
stream f = Nu (c f id)

と定義してもよい。この点については末尾に補足する。

有限オートマトンと余代数

多項式型

ここで型 $A$ の多項式型 $A^\star$ という概念が重要な役割を果たすので導入しておく。まず、値を持たないことを意味する型を $1$ と書く。また型 $A$ の値ないしは型 $B$ の値を取る型を $A+B$ と書くことにする。$+$の記法はそのまま論理和「ないしは」と整合している。多項式型 $A^\star$ は次の式で定義される。

$$A^\star = 1 + A + A\times A + A\times A\times A + \cdots$$

すなわちその値は値なし $\mathrm{nil}$ であったり、$a_0$ であったり、$(a_0,a_1)$ や $(a_0, a_1, a_2)$ であったりする。多項式型とは任意個数の値を格納できる型、要するにリストのことである。

$$\begin{split} A^\star &= 1 +A + A\times A + A\times A\times A + \cdots \\ &= 1 + A \times (1 + A + A\times A +\cdots) \\ &= 1 + A \times A^\star \end{split}$$

であるから、$A^\star$ も不動点として構成できそうだということが分かる。実際、

data ListF a b = Nil | Cons a b
instance Functor (ListF a) where
    fmap f (Cons a b) = Cons a (f b)
    fmap f Nil = Nil
type List a = Fix (ListF a)

と定義すれば List a が $A^\star$ に相当する。いま Nil | Cons a b は $1 + A\times B$ に対応している。ListF a は函手 $F_A(-) = 1 + A\times(-)$ でありその不動点としてList aが構成されている。

やはり便宜のためList a とリスト[a]の変換関数を定義しておく。

fromList :: [a] -> List a
fromList = unfoldFix fromListF
  where
    fromListF (x:xs) = Cons x xs
    fromListF [] = Nil

toList :: List a -> [a]
toList = foldFix (elimListF [] (:)) 
  where
    elimListF x f (Cons a b) = f a b
    elimListF x f Nil = x

Stream aの場合とは異なりList aと[a]との間に全単射が存在しているため双方向の写像が定義できている。関数名の不適切さには目を瞑られたい。

有限オートマトン

有限オートマトンは状態 $S$ および、入力$A$による状態の遷移$S\rightarrow S$ と出力$S\rightarrow B$ を持つ。入力$A$による状態の遷移$S\rightarrow S$は

$$A\times S \overset{\delta}{\longrightarrow} S$$

で表されるが、積 $A\times (-)$ と冪 $(-)^A$ の随伴性を用いることで

$$S \overset{\delta}{\longrightarrow} S^A$$

でこれを捉えられる。出力 $\epsilon : S\rightarrow B$ と合わせれば

$$S \overset{\langle \delta,\epsilon\rangle}{\longrightarrow} S^A\times B$$

なる余代数が有限オートマトンを決定することが分かる。

いま $F_{A,B}(S) = S^A\times B$ また$c = \langle \delta, \epsilon \rangle$とし、構築すべき余代数を

$$S \overset{c}{\longrightarrow} F_{A,B}(S)$$

と書こう。記号をこれに合わせると実装は

data F a b c = Pair (a -> c) b 
getF (Pair f b) = f
getB (Pair f b) = b

instance Functor (F a b) where
  fmap f (Pair g b) = Pair (f.g) b

c :: S -> F A B S
c s = Pair (delta s) (epsilon s)

となる。未定義の部分については有限オートマトンの具体形が必要である。ここでは"Introduction to Coalgebra"に掲載されていた

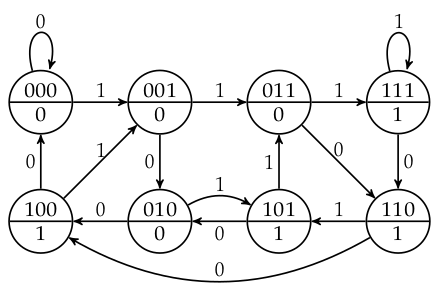
を実装してみよう。定義はひたすらしこしこ書くのみである。

data B = O | I deriving Show 
type S = (B,B,B)
type A = B

epsilon :: S -> B 
epsilon (I,I,I) = I
epsilon (I,O,O) = I
epsilon (I,O,I) = I
epsilon (I,I,O) = I
epsilon (O,O,O) = O
epsilon (O,O,I) = O
epsilon (O,I,I) = O
epsilon (O,I,O) = O

delta :: S -> A -> S
delta (O,O,O) O = (O,O,O)
delta (O,O,I) O = (O,I,O)
delta (O,I,I) O = (I,I,O)
delta (I,I,I) O = (I,I,O)
delta (O,O,O) I = (O,O,I)
delta (O,O,I) I = (O,I,I)
delta (O,I,I) I = (I,I,I)
delta (I,I,I) I = (I,I,I)

delta (I,O,O) O = (O,O,O)
delta (O,I,O) O = (I,O,O)
delta (I,O,I) O = (O,I,O)
delta (I,I,O) O = (I,I,I)
delta (I,O,O) I = (O,O,I)
delta (O,I,O) I = (I,O,I)
delta (I,O,I) I = (O,I,I)
delta (I,I,O) I = (I,O,I)

いま 0, 1 を O, I に代替している。

さて、この有限オートマトンの振る舞いを得るために終余代数を考えよう。函手$F_{A,B}(-) = (-)^A\times B$ の不動点 $\mathrm{Fix}\, F_{A,B}$ は $B^{A^*}$ で与えられる。実際、

$$\begin{split} B^{A^*} &= B ^ {1 + A + A\times A + \cdots} \\ &= B ^ {A + A\times A + \cdots} \times B \\ &= (B ^ {1 + A + A\times A + \cdots})^A \times B \\ &= (B^{A^*})^A\times B \\ &= F_{A,B}(B^{A^*}) \end{split}$$

である。$B^{A^*}$ は List a -> b であり、

$$B^{A^*} = B ^ {1 + A + A\times A + \cdots} = B\times B^A \times B^{A\times A} \times \cdots$$

と書けば、有限オートマトンに任意長さの入力 $(a_0,a_1,...,a_k)$ を与えた時の出力値 $b_{01...k}$ を計算することが分かる。入力が空 $()$ の場合は初期値が返される。なおこのような算法が成立する背景、すなわち圏に積$\times$, 余積$+$, 冪$(-)^{(-)}$ が定義されていて互いに整合していることはあらかじめ確認しておく必要がある。

Streamの場合と同様に振る舞いは余帰納的定義

$$S \overset{b}{\longrightarrow} \mathrm{Fix}\,F_{A,B}$$

すなわち

b :: S -> Fix (F A B)
b = unfoldFix c

で与えられる。bには初期状態を渡す。

ところで、いま$\mathrm{Fix}\, F_{A,B}$ は $B^{A^*}$ で与えられるといっても、その対応はStream a のときほどは自明ではない。したがってその等価性

$$\mathrm{Fix}\, F_{A,B} \overset{\simeq}{\longrightarrow} B^{A^*}$$

を関数で具体的に示す必要がある。$B^{A^*}$ はList A -> B のことであった。その関数はたとえば次のapplyで与えることができる。

apply :: Fix (F A B) -> List A -> B
apply f as =
  case as of
    Fix Nil -> getB $ unFix f
    Fix (Cons a as) -> apply ((getF $ unFix f) a) as

いくつか具体例を計算してみよう。

ghci> (apply $ b (O,O,O)) $ fromList [I,O,O]
I
ghci> (apply $ b (O,O,O)) $ fromList [I,I,O,I,I]
O
ghci> (apply $ b (I,I,O)) $ fromList [I,I,O]
I

上の状態遷移図を辿ると正しく計算できていることが確認できる。

（補足）帰納／余帰納について

ここでの内容は Benjamin Pierceによる "Types and Programming Languages" を参考にしている。

対象と射 $X\rightarrow A$ の伝統的な例は部分集合のinjection $X\subseteq A$ であり、その意味で圏 $\mathcal C$ は集合、とくに空間性を備えたその位相的構造、ないしは順序構造の一般化になっている（圏$\mathcal C$はさらに米田埋め込みで$\mathcal{Sets}^{\mathcal{C}^{\mathrm{op}}}$ に埋め込まれ、この函手圏が空間の最も圏論的な姿であるといえる）。だから圏を部分集合の類比として理解できることがある（エレメンタリートポスの構造が入るとこの類似はいっそう正確になる）。

写像$F:A\rightarrow A$ に対して

1. $F(X) \subseteq X$ のとき $X$ は $F$-closed であるという。
2. $X \subseteq F(X)$ のとき $X$ は $F$-consistent であるという。
3. $X = F(X)$ のとき $X$ は $F$ の不動点であるという。

このとき次の性質が成り立つ（Knaster-Tarski の定理）。

$$\mu F = \bigcap_{X:F\text{-closed}} X,\quad \nu F = \bigcup_{X:F\text{-consistent}} X$$

ここで $\mu F$ は $F$ の最小不動点、$\nu F$ は $F$ の最大不動点である。ここで定義から明らかな次の推論を帰納法および余帰納法と定義する。

1. 帰納法： $X$ が $F$-closed ならば $\mu F \subseteq X$
2. 余帰納法： $X$ が $F$-consistent ならば $X \subseteq \nu F$

以上の内容を圏論に翻案すると次のように言葉を定義できよう。

1. $F$-代数 $F(X) \rightarrow X$ に対して始代数 $F(\mu F)=\mu F$ が存在するとき、帰納（再帰）射 $\mu F \rightarrow X$ が存在する。
2. $F$-余代数 $X\rightarrow F(X)$ に対して終余代数 $\nu F = F(\nu F)$ が存在するとき、余帰納（余再帰）射 $X \rightarrow \nu F$ が存在する。

上ではまさしく余帰納射 $X \rightarrow \nu F$ によって Stream や有限オートマトンを扱ったのであった。

$F$-代数ないしは帰納を扱う材料もすでに揃っているのでまとめておこう。Stream a の擬コードによる定義は

Stream a = Pair a (Stream a)

であった。したがって既存のStream に a 型の値を追加し、新たなStream とすることができるはずである。すなわち次なる関数が存在するはずである。

Pair a (Stream a) -> Stream a

これはまさしく代数 $P_A(S) =A\times S\rightarrow S$ である（Wiktionary によると 代数 algebra のアラビア語語源 al-jabr の意味は「再結合 reunion 」であり、まさにそのことと整合している）。Data.Fix ではFixをそのまま該当する関数として用いることができる。実際、次のような挙動を示す。

ghci> toList $ stream (+1) 1
[1,2,3,4,5,6,7,8,9,10,...
ghci> toList $ Fix $ Pair 0 (stream (+1) 1)
[0,1,2,3,4,5,6,7,8,9,..

今度はListを使ってみる（Streamの節と同名異定義の関数を用いているので注意せよ）。次のような関数を定義しよう。

f :: ListF Int Int -> Int
f (Cons a b) = a * b
f Nil = 1

prod :: List Int -> Int
prod = foldFix f

fは数値の積 $\times:\mathbb{N}\times \mathbb{N}\rightarrow \mathbb{N}$ であり、代数を与える。List a型は不動点Fix (ListF a)として定義されていた。終余代数と同様に始代数$F(\mathrm{Fix}\,F)\rightarrow \mathrm{Fix}\,F$ が考えられる。また余代数から終余代数への射を考えたように、今後は始代数から代数への射

$$\begin{array}{ccc} F(\mathrm{Fix}\,F) & \longrightarrow & F(A) \cr \downarrow &&\downarrow \cr \mathrm{Fix}\,F & \overset{s}{\longrightarrow} & A \end{array}$$

を考える。それは

foldFix :: Functor f => (f a -> a) -> Fix f -> a

で与えられ、catamorphismとも呼ばれる。prod は総積関数になる。実際、

ghci> prod $ fromList [1,2,3,4,5]
120

である。ここで

g :: Int -> List F Int Int
g 0 = Nil
g n = Cons n (n-1)

とすればgは余代数を与える。$\mathrm{Fix}\,F$ における対応する振る舞いは

ghci> toList $ unfoldFix g 5
[5,4,3,2,1]

となる。f と g を組み合わせれば階乗関数が作れる。

ghci> foldFix f $ unfoldFix g 5
120

したがって俗に言われる「階乗の再帰的定義」は帰納（再帰）と余帰納（余再帰）の双方がこれを構成しており語義を混乱させている。

個人的思想的なこと

時間発展方程式に初期値を与えて軌道を求める、古典力学でおなじみの行為は、余代数の終余代数への余帰納射を与えることであった。私たちに観察できるのはその振る舞いのみであるが、しばしば（それが決定的であれ非決定的であれ、確率的であれ）そこに構造を見出すことで思考を巡らせている。参考文献"Introduction to Coalgebra"では有限オートマトンにおいて振る舞いの圏と構造の圏が随伴であることを示している。

私たちの時間観は巨視的な履歴現象に基づいており、「順を追って」考える習慣のある人間にとって、構造と振る舞いとしての余代数と終余代数はかなり卑近である。一方で自然界の振る舞いは元をただすと量子現象であり、自発的確率的な相互作用が基本にある。そこには私たちの時間観を可能にするものがあるが、私たちの時間観をどこまで適用できるかは自明ではない。余代数の概念をうまく「量子化」できればそのような問題にもアプローチできるかもしれない。

参考文献まとめ

1. Bart Jacobs ,"Introduction to Coalgebra"
2. Benjamin Pierce, "Types and Programming Languages"