TimesNet解説まとめ -時系列予測モデル-
今回は時系列予測モデルのTimesNetを解説します。
原論文:TimesNet: Temporal 2D-Variation Modeling for General Time Series Analysis
この記事は、TimesNet: The Latest Advance in Time Series Forecastingを参考に記述しています。英語が読める方はこちらを確認して下さい。
1. TimesNet
1.1 概論
機械学習による時系列予測モデルは、2020年のN-BEATS、2022年のN-HiTS、2023年3月のPatchTSTのように新しいモデルが発表されてきました。
TimesNetは2023年4月に発表された時系列予測モデルです。一次元の時系列データを二次元に変換することにより、データの依存関係を捉える力が向上しました。
その性能は抜群で、短期予測、長期予測、欠損補完、分類、異常検知の5つの分野でSOTAを達成しました。
これまで(MLP,Transformerベース)と異なり、CNNベースのモデルで最先端の成果を達成しているため、時系列分析の基礎モデルとして最適候補になっています。これは、CNNがデータ量に対して効率的な予測を提供するためです。
1.2 経緯
TimesNetアーキテクチャの背後にあるのは、現実にある時系列の多くが複数の周期性を持つという認識です。
例えば、気温は昼と夜、夏と冬のように日単位と年単位の周期性を持ちます。これらの期間は複数に重なり合い、相互に影響を与えているため、個別に分離してモデル化することが困難になっています。
これらの周期性をうまく捉えるために、TimesNetの著者達は二次元空間で時系列を再構成して、「周期内変動」と「周期間変動」をモデル化することを提案しました。
上記の例で表すと、周期内変動は1日の気温がどのように変化するのかを示し、周期間変動は気温が日毎、年毎にどのように変化するのかを示します。
これらを念頭に置いて、モデルのアーキテクチャを見ていきましょう。
2. TimesNetのアーキテクチャ
2.1 アーキテクチャ
では、TimesNetのアーキテクチャを見てみましょう。
・TimesNetアーキテクチャ
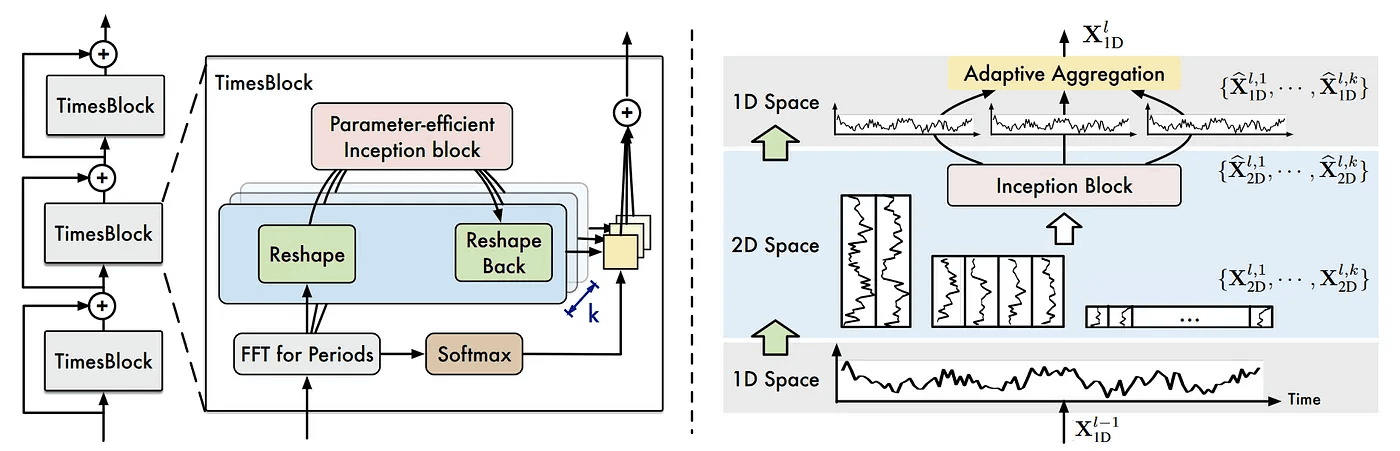
この図から、TimesNetは残差接続を持つTimesBlockが積み重ねられたものである事が分かります。
また各TimesBlockでは、時系列データの様々な周期性を見つけるために、最初にFFTを通している事が分かります。
次にFFTに通過後の一次元波形が二次元データとして再構成され、Inceptionブロックで学習および予測が行われます。最後にこの出力をAdaptive Aggregation(適応集約)を使用して一次元データに変更します。
ここからは、それぞれの処理について細かくみていきましょう。
2.2 期間内変動と期間間変動を捉える
著者らは、一次元のデータを二次元空間に変更して、期間内および期間間の変動を同時に捉えることを提案しています。
・期間内変動と期間間変動(intraperiod and interperiod variations)

この図は、様々な長さで分割された期間に対する期間内変動と期間間変動のイメージです。
赤い四角形は期間内のデータの変化、青い四角形は期間と期間の間のデータの変化を示しています。
この変動は二次元空間で表現され、期間間変動は垂直方向(青い矢印)、期間内変動は水平方向(赤い矢印)で表現されます。
2.3 期間の特定
上記では、時系列データを分割して二次元データを作成しました。では、このデータを分割する期間の長さ(period)はどのように決めれば良いでしょうか。
これは、フーリエ変換によって求める事ができます。
・二次元配列作成イメージ

図の左上に示すように、フーリエ変換は時系列データの各周波数成分の振幅の大きさを求める事ができます。(フーリエ変換についてはこちらでも解説しています)
FFTによって得られた振幅が最も大きい周波数が、最もデータの周期性と関係のあると考えられるため、この周期でデータの分割を行います。
2.4 TimesBolck
FFTによって得られた周波数で分割したデータを積み重ねて、2次元配列が作成されると、以下に示すようにデータがInceptionブロックに送られます。
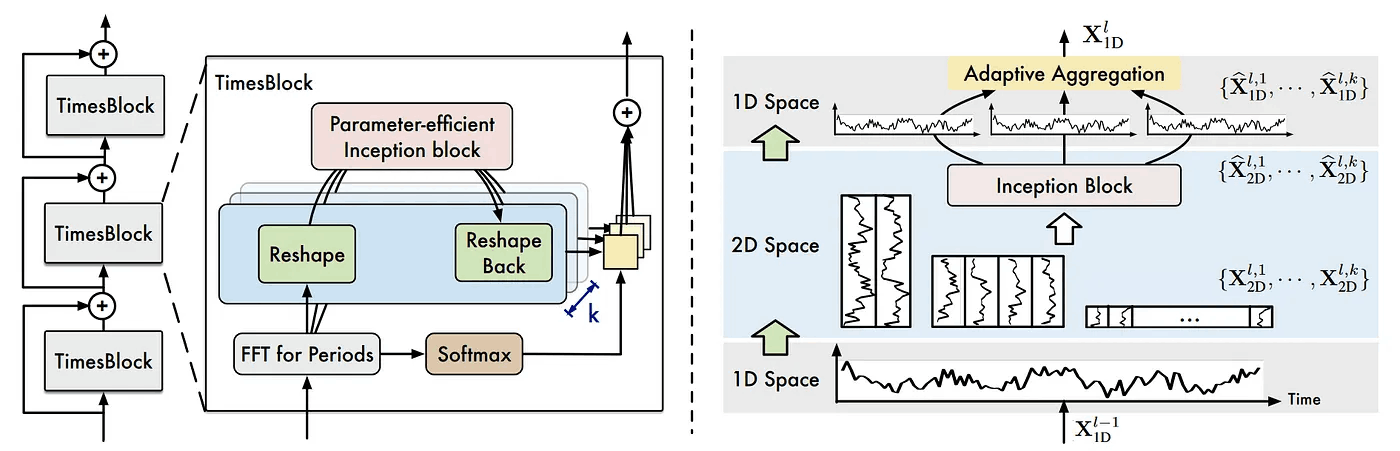
Inceptionモジュールの主なアイデアは、データを疎に保つことでデータを効率的に表現することです。これにより、計算効率を維持しながらNNのサイズを増やす事ができます。
これは、様々な畳み込みとプーリングを行った結果を結合することで実現されます。
TimesNetのアーキテクチャでは、Inceptionモジュールは以下のようになります。
・Inceptionモジュール
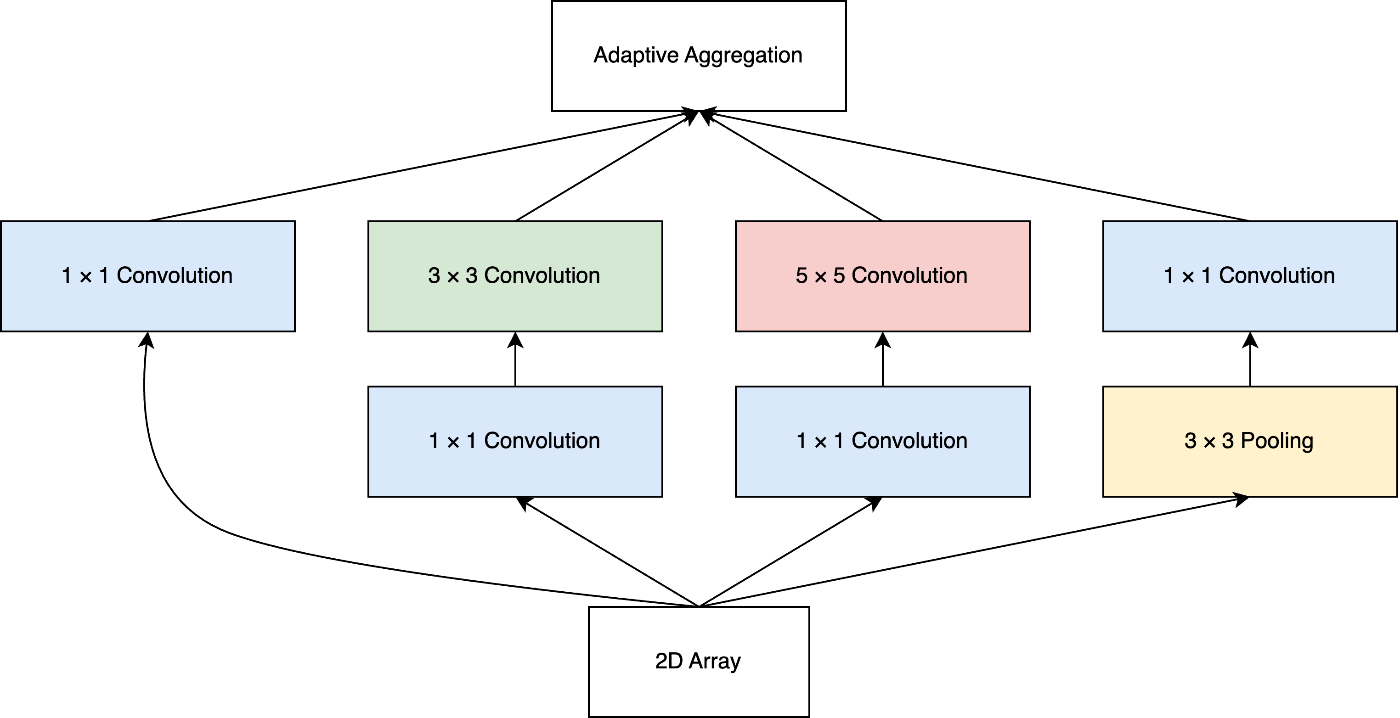
Inceptionモジュールでは畳み込みが行われるため、二次元配列が一次元配列に変換されます。
2.4.1 Adaptive Aggregation
TimesNetのInceptionモジュールの特徴として、Adaptive Aggregation(適応集約)があります。
TimesNetでは、周波数毎にFFTで得られる振幅の大きさが異なります。その違いによる各期間データの重要性を表現するために、Adaptive Aggregation(適応集約)が使用されます。
具体的には、Adaptive AggregationがInceptionモジュールからの特徴に加えて、「各期間の相対的な重要度」を利用できるように、FFTの出力もソフトマックス層に通された後、Adaptive Aggregationに渡されます。
このAdaptive Aggregationの出力が単一のTimesBlockの出力です。このTimesBlockが残差接続を伴って積み重ねられたものが、TimesNetモデルです。
2.5 結論
TimesNetはフーリエ変換を用いて分割すべき期間を見つけ出し、データを二次元配列にして、重み付けされた特徴を利用して学習を行うモデルでした。
また残差接続を利用することで、線型写像も学習する事ができるようになるため、より表現力が高くなっています。
3. TimesNetによる予測
では、実際にTimesNetによる予測をmarcopeixさんの実装を参考に解説していきます。
3.1 ライブラリのインポート
必要なライブラリのインポートを行います。ここではNIXTLAのNeuralForecastで利用可能な実装を使用します。
# ライブラリのインポート
!pip install neuralforecast
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from neuralforecast.core import NeuralForecast
from neuralforecast.models import NHITS, NBEATS, TimesNet
from neuralforecast.losses.numpy import mae, mse
plt.rcParams["figure.figsize"] = (9,6)
3.2 データのロード
データをロードします。今回は時系列予測のベンチマークとしてよく利用されている、変圧器の油温予測を行うEttデータセットを使用します。
# Ettデータのロード
df = pd.read_csv('/kaggle/input/etth1-data/etth1.csv')
df['ds'] = pd.to_datetime(df['ds'])
df.head()
# 可視化
fig, ax = plt.subplots()
ax.plot(df['y'])
ax.set_xlabel('Time')
ax.set_ylabel('Oil temperature')
fig.autofmt_xdate()
plt.tight_layout()
・Ettデータセット

3.3 モデル定義
モデルを定義します。
予測期間は長期予測の一般的な期間である96時間に設定します。
N-BEATS、N-HiTS、TimesNetのモデルのリストを定義し、NeuralForecastsオブジェクトをインスタンス化します。
すべてのモデルのデフォルトパラメータをそのまま使用し、エポックの最大数を50に制限します。デフォルトでは、TimesNetはデータ内の最も重要な期間の上位5つを選択します。
# モデル定義
horizon = 96
models = [NHITS(h=horizon,
input_size=2*horizon,
max_steps=50),
NBEATS(h=horizon,
input_size=2*horizon,
max_steps=50),
TimesNet(h=horizon,
input_size=2*horizon,
max_steps=50)]
# インスタンス化
nf = NeuralForecast(models=models, freq='H')
3.4 モデル評価
3.4.1 交差検証
交差検証を使用して、モデルの性能を評価します。(Testデータセットに対して予測を行います)
# 交差検証
preds_df = nf.cross_validation(df=df, step_size=horizon, n_windows= 2 )
# 各モデル予測結果を表示
preds_df.head()
# 各モデル予測を可視化
fig, ax = plt.subplots()
ax.plot(preds_df['y'], label='actual')
ax.plot(preds_df['NHITS'], label='N-HITS', ls='--')
ax.plot(preds_df['NBEATS'], label='N-BEATS', ls=':')
ax.plot(preds_df['TimesNet'], label='TimesNet', ls='-.')
ax.legend(loc='best')
ax.set_xlabel('Time steps')
ax.set_ylabel('Oil temperature')
fig.autofmt_xdate()
plt.tight_layout()
plt.savefig('forecast.png')
plt.show()
・各モデルの予測結果

・各モデルの予測結果の可視化
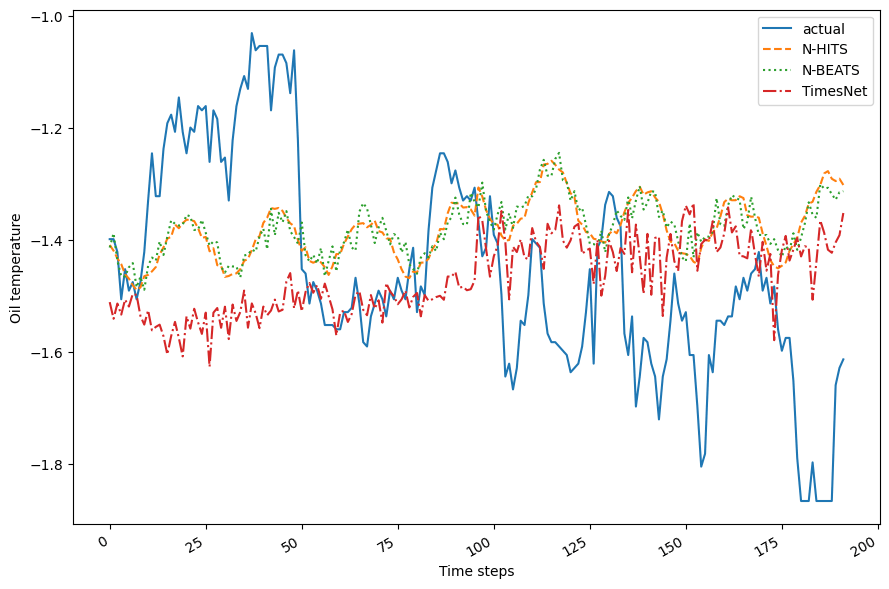
上記の結果では、どのモデルもデータの変動を予測できていないように見えます。
またN-BEATSとN-HiTSは、TimesNetの予測とは異なり、元データの周期的なパターンを少し捉えていますが、予測と呼ぶには精度が不十分です。
3.4.2 MAE,MSE
ここで、予測精度を定量的に評価するために、MAE(平均絶対誤差)とMSE(平均二乗誤差)を計算します。
MAEとMSEは、予測結果が元のデータからどの程度離れていたか、という指標で精度を評価します。
# MAE,MSEの計算
data = {'N-HiTS': [mae(preds_df['NHITS'], preds_df['y']), mse(preds_df['NHITS'], preds_df['y'])],
'N-BEATS': [mae(preds_df['NBEATS'], preds_df['y']), mse(preds_df['NBEATS'], preds_df['y'])],
'TimesNet': [mae(preds_df['TimesNet'], preds_df['y']), mse(preds_df['TimesNet'], preds_df['y'])]}
metrics_df = pd.DataFrame(data=data)
metrics_df.index = ['mae', 'mse']
metrics_df.style.highlight_min(color='lightgreen', axis=1)
・MAE,MSE
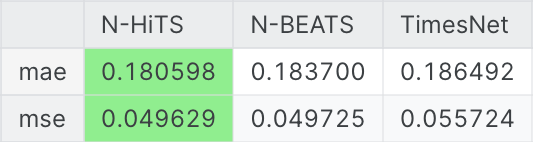
結果を見ると、N-HiTSがどちらの指標でも優れているようです。
※ N-BEATSもほぼ同様の精度を達成しています
従って、TimesNetは最高精度を達成できなかったことになります。しかし、注意すべきは単純な96×2stepの予測タスクのみの比較であり、ハイパーパラメータのチューニングなども行われていないということです。
3.5 結論
TimesNetとN-HiTS、N-BEATSについて、簡単な時系列予測モデルを比較したところ、TimesNetは両モデルに及びませんでした。
しかし、TimesNetの構想である、「周期性を捉えるために、フーリエ変換を用いてデータを一次元から二次元に変換、重み付けしたものを特徴として扱う」という考え方は、幅広いタスクへの応用が考えられます。
また各予測における最適な手法は異なるため、様々なモデルを試すことが推奨されます。
まとめ
今回はTimesNetの概要から、他モデルとの比較までを行いました。
TimesNet解説は今回で終了です。読んでいただきありがとうございました。
参考
(1)marcopeix/time-series-analysis/TimesNet.ipynb
(2)TimesNet: The Latest Advance in Time Series Forecasting
(3)TimesNet: Temporal 2D-Variation Modeling for General Time Series Analysis
(4)Going Deeper with Convolutions(GoogLeNet)
Discussion