Zenn
📊

【統計検定準1級】ガンマ分布

2024/07/30に公開
数理統計
ガンマ分布
統計検定準一級
tech

はじめに

この記事では、統計検定準1級取得に向けて学習したことをまとめていきます。
工学系の数学ではなく数理あるあるの、論述ゴリゴリな解答になっていると思いますのであらかじめご了承ください。
注意：さらに計算過程は数学文化の『省略の美』を無視してエレファントに書いています。

【リンク紹介】
・統計検定準1級のまとめ記事一覧
・これまで書いたシリーズ記事一覧

学習書籍について

この記事では「統計学実践ワークブック」を中心に、学んだことをまとめていきます。記事を読んで本格的に勉強してみたいなと思った方は、是非ご購入を検討なさってください。


参考書籍について

統計実践ワークブックは、大量の知識項目と問題が収められている反面、計算過程や知識背景が大きく省略されているため、知識体系をきちんと学ぶ参考書として東京大学から出版されている名著「統計学入門」を使っています。
※ワークブックとしては素晴らしい質だと思いますが、どうしてもその内容量とページ数の都合上、問題のない範囲で削除されているということです。人によっては1冊で問題ない方もおられると思いますが、私には無理でした。


ガンマ分布

確率変数Xが連続型であるとする。このXとa > 0, b > 0に対し、確率密度関数fが

f(x) = \cfrac{1}{\Gamma (a) \ b^a} x^{a - 1} e^{- \frac{x}{b}} \hspace{5mm} (x > 0)

であるとき、この確率密度関数fを形状母数a、尺度母数bのガンマ分布(gamma distribution)といい、Ga(a, b)と表す。ただし、

\Gamma(a) = \int_{0}^{\infty} x^{a - 1} e^{-x} dx \hspace{5mm} (a > 0)

と定め、\Gamma(a)をガンマ関数という。これはf(x)を積分した際に1になるようにする役割がる。

特にa = 1の場合のガンマ分布Ga(1, b)は、\lambda = \frac{1}{ \ b \ }とした指数分布Exp \left( \frac{1}{b} \right)である。

グラフの描画

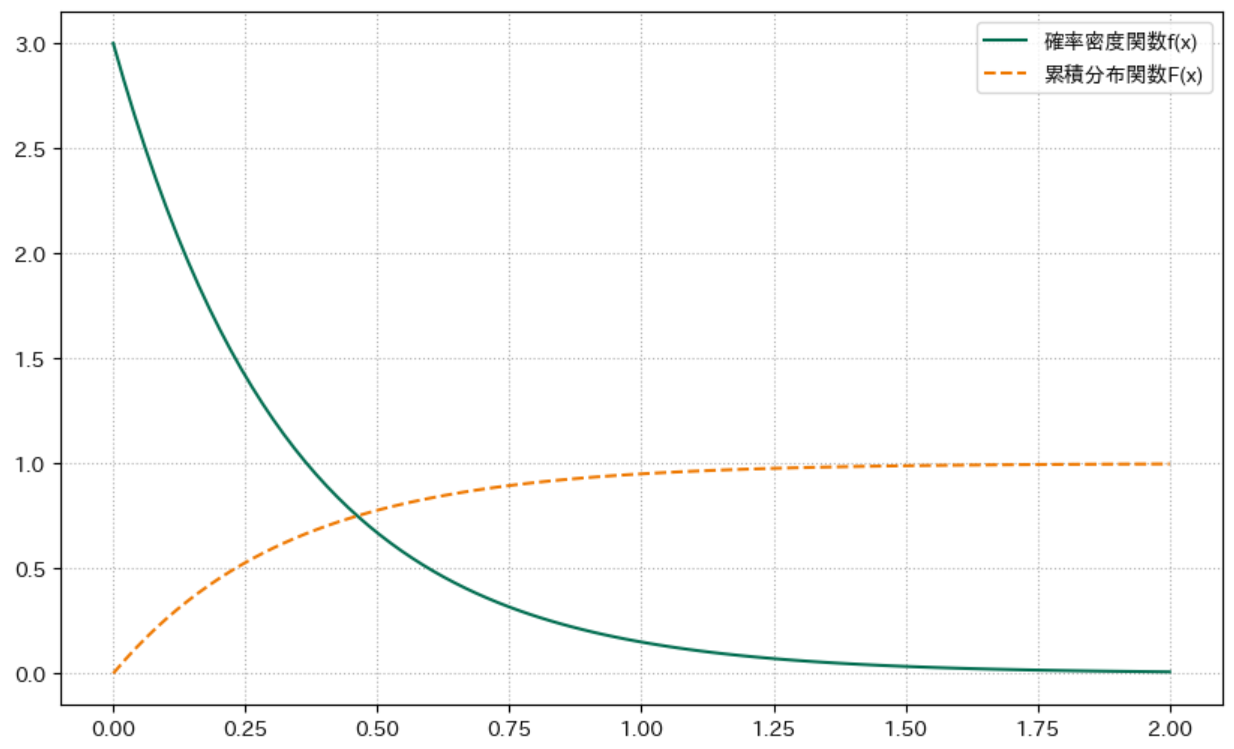
ガンマ分布は指数分布を一般化したものであり、a = 1, b = \displaystyle\cfrac{1}{3}とすると、指数分布のグラフと同じものになっていることが確認できる。

コードはこちら

参考資料→Pythonで理解する統計解析の基礎
※ガンマ分布は記載がなかったので自分で作成したものになります。

import numpy as np
import matplotlib.pyplot as plt
import japanize_matplotlib                    # グラフ上での日本語表示
from scipy import stats, integrate
from scipy.optimize import minimize_scalar    # 関数の最小値を求める

# 表示桁数を小数点以下第３位に設定
%precision 3

# [Jupyter notebook only]
# グラフ表示を非インタラクティブモード(jupyter notebook内に表示)に設定
# インタラクティブモードだと別ウィンドウで表示される
%matplotlib inline

"""""""""""""""""""""""""""""""""""""""""""""""""""
関数名：Ga(a, b)
機　能：ガンマ分布
引　数：a, b
戻り値：連続型確率変数と確率密度関数（X, f）
"""""""""""""""""""""""""""""""""""""""""""""""""""

def Ga(a, b):
    # 連続型確率変数
    X = [0, np.inf]

    # ガンマ関数の被積分関数
    def Gamma_func(x):
        return (x**(a - 1)) * (np.exp(-x))

    # ガンマ関数
    Gamma = integrate.quad(Gamma_func, 0, np.inf)[0]
    
    # ガンマ分布
    def f(x):
        if x >= 0:
            return (1 / (Gamma * b**a)) * (x**(a - 1)) * np.exp(-x / b)
        else:
            return 0
            
    return X, f

# ラムダ式を用いた場合
# def Ga(a, b):
#     X = [0, np.inf]

#     # ガンマ関数
#     Gamma = integrate.quad(lambda x: (x**(a - 1)) * (np.exp(-x)), 0, np.inf)[0]
    
#     # ガンマ分布
#     def f(x):
#         if x >= 0:
#             return (1 / (Gamma * b**a)) * (x**(a - 1)) * np.exp(-x / b)
#         else:
#             return 0
            
#     return X, f

# 指数分布と同じ形になる条件にした
a = 1
b = 1/3
Xf = Ga(a, b)

check_prob(Xf)

# 指数分布と同じ形になる条件にした
plot_prob(Xf, 0, 2)
基本関数
import numpy as np
import matplotlib.pyplot as plt
import japanize_matplotlib                    # グラフ上での日本語表示
from scipy import stats, integrate
from scipy.optimize import minimize_scalar    # 関数の最小値を求める

# 表示桁数を小数点以下第３位に設定
%precision 3

# [Jupyter notebook only]
# グラフ表示を非インタラクティブモード(jupyter notebook内に表示)に設定
# インタラクティブモードだと別ウィンドウで表示される
%matplotlib inline

# グラフの線の種類
linestyles = ['-', '--', ':']

"""""""""""""""""""""""""""""""""""""""""""""""""""
関数名：E(Xf, g = lambda x: x)
機　能：連続型確率変数（確率変数の関数）の期待値を返す
引　数：連続型確率変数と確率関数X(タプル)
       連続型確率変数Xの関数g(初期値:恒等関数)
戻り値：期待値
"""""""""""""""""""""""""""""""""""""""""""""""""""

def E(Xf, g = lambda x: x):
    X = Xf[0]    # 連続型確率変数
    f = Xf[1]    # 確率密度関数

    def integrand(x):
        return g(x) * f(x)
    
    expection = integrate.quad(func = integrand,    # 被積分関数
                               a    = -np.inf,      # 積分区間
                               b    = np.inf        # 積分区間
                              )[0]
    
    return expection

"""""""""""""""""""""""""""""""""""""""""""""""""""
関数名：V(Xf, g = lambda x: x)
機　能：連続型確率変数（確率変数の関数）の分散を返す
引　数：連続型確率変数と確率関数X(タプル)
       連続型確率変数Xの関数g(初期値:恒等関数)
戻り値：分散
"""""""""""""""""""""""""""""""""""""""""""""""""""

def V(Xf, g = lambda x: x):
    X = Xf[0]    # 連続型確率変数
    f = Xf[1]    # 確率密度関数
    expection = E(Xf, g)

    def integrand(x):
        return (g(x) - expection) ** 2 * f(x)
    
    variance = integrate.quad(func = integrand,    # 被積分関数
                              a    = -np.inf,      # 積分区間
                              b    = np.inf        # 積分区間
                             )[0]
    
    return variance

"""""""""""""""""""""""""""""""""""""""""""""""""""
関数名：check_prob(Xf)
機　能：連続型確率変数が確率の性質を満たしているかを確認する
引　数：連続型確率変数と確率密度関数(タプル)
戻り値：なし
"""""""""""""""""""""""""""""""""""""""""""""""""""

def check_prob(Xf):
    X = Xf[0]    # 連続型確率変数
    f = Xf[1]    # 確率密度関数
    
    f_min = minimize_scalar(f).fun
    assert f_min >= 0, '確率密度関数が負の値をとります'
    
    prob_sum = np.round(integrate.quad(f, -np.inf, np.inf)[0], 6)
    assert prob_sum == 1, f'確率の和が{prob_sum}になりました'

    print(f'期待値は{E(Xf):.3f}')
    print(f'分散は{V(Xf):.3f}')

"""""""""""""""""""""""""""""""""""""""""""""""""""
関数名：plot_prob(Xf, x_min, x_max)
機　能：確率密度関数と期待値を図示する
引　数：連続型確率変数と確率密度関数X(タプル)
       定義域の最低値
       定義域の最大値
戻り値：なし
"""""""""""""""""""""""""""""""""""""""""""""""""""

def plot_prob(Xf, x_min, x_max):
    X = Xf[0]    # 連続型確率変数
    f = Xf[1]    # 確率密度関数
    
    # 累積分布関数
    def F(x):
        return integrate.quad(f, -np.inf, x)[0]

    xs = np.linspace(x_min, x_max, 100)

    fig = plt.figure(figsize = (10, 6))
    ax  = fig.add_subplot(1, 1, 1)

    # 確率密度関数のグラフ
    ax.plot(xs, [f(x) for x in xs], label = '確率密度関数f(x)', color = '#006C4F')
    
    # 累積分布関数のグラフ
    ax.plot(xs, [F(x) for x in xs], label = '累積分布関数F(x)', ls = '--', color = '#ee7800')

    # グラフ設定
#   ax.set_xticks(np.append(X, E(Xf))) # x目盛値
#   ax.set_ytickx()                    # y目盛値  
#   ax.set_xlim()                      # x軸の範囲
#   ax.set_ylim()                      # y軸の範囲
#   ax.xlabel()                        # x軸ラベル
#   ax.ylabel()                        # y軸ラベル    
    ax.legend()                        # 凡例

    # 描画
    plt.show()

ガンマ分布の期待値

E[X]：Xの期待値

E[X] = ab

ガンマ分布の分散

V[X]：Xの分散

V[X] = ab^2

ガンマ分布のモーメント母関数

m(\theta) = E[e^{\theta X}]：Xのモーメント母関数

\begin{alignat*}{2} m(\theta) &= E[e^{\theta X}] \\ &= (1 - b \theta)^{-a} \hspace{5mm} \left( \theta < \cfrac{1}{ \ b \ } \right) \\ \end{alignat*}

参考資料

\bf{\textcolor{red}{記事が役に立った方は「いいね」を押していただけると、すごく喜びます \ 笑}}
ご協力のほどよろしくお願いします。

Discussion