🦾

局所ガウスモデルとはなんぞや？

2023/12/09に公開

本記事の目的

こんにちは．この記事は，日本音響学会学生・若手フォーラム Advent Calendar 2023 の3日目 (?) として書いています．さて，何の話をしようか迷ったのですが，局所ガウスモデル (LGM) [N. Q. K. Duong+ 2011] について語ってみたいと思います．皆さんLGMはご存じですか？ ↓みたいなやつです．

\mathbf{x}_{tf} \sim \mathcal{N}_\mathbb{C}(\bm{0}, \lambda_{tf} \mathbf{H}_{f})

このモデルは，ブラインド音源分離 (BSS) で良く使われる生成モデルで，モノラル信号の板倉斎藤ダイバージェンス (IS-div.) [C. Févotte+ 2009] とも深い関わりがあります．本記事では，LGMの解釈や妥当性を，時間波形の生成モデルから順を追って解説してみたいと思います．

モノラル時間波形のガウス過程表現

LGMやIS-div.では，時間波形がガウス過程 (GP; 解説は [赤穂 2018] や [持橋+ 2019] など) に従っていると (暗に) 仮定されています．このモデルでは， $N$ 点の時刻 $t_n \in \mathbb{R}_+$ ( $n=1, \ldots, N$ ) における，時間波形 $\mathbf{y} \triangleq \{ y_n \in \mathbb{R} \}_{n=1}^N$ が，以下の零平均ガウス分布に従っていると仮定します．

\mathbf{y} \sim \mathcal{N}\left(\mathbf{0}, \mathbf{R} \right)

ここで $\mathbf{R}$ は， $N\times N$ の半正定値対称行列 (共分散行列) を表していて， $\mathbf{R}$ の $(n_1, n_2)$ 要素は，対応する時刻を引数とする関数 $r(t_{n_1}, t_{n_2})$ から生成されます．この関数 $r: \mathbb{R}_+ \times \mathbb{R}_+ \rightarrow \mathbb{R}$ はカーネル関数と呼ばれ，時間波形の形状を決定します．

例えば，角速度 $\omega$ の周期カーネルは下記で定義され，周期 $1/\omega$ の周期的な信号を表現します．

r(t_1, t_2) \propto \exp(-\sin(\pi\omega |t_1 - t_2|)^2)

周期200としてこのカーネルから $\mathbf{R}$ を構成し，実際に $\mathbf{y}$ を3つサンプルしてみた例が以下です．周期性を持った色んな波形が生成されていますね．

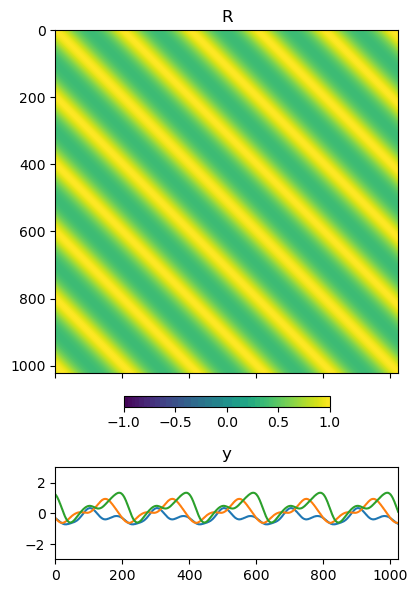
他にも，角速度 $\omega$ のスペクトルカーネル [Lázaro-Gredilla+ 2010] は，下記で定義され周期 $1/\omega$ の三角関数を表します．

r(t_1, t_2) \propto \cos(2\pi \omega (t_1 - t_2))

このカーネルを用いた $\mathbf{R}$ と $\mathbf{y}$ の例は次の通りです．ガウス分布からサンプルしているのに，綺麗に三角関数が出てくるのは面白いですよね．

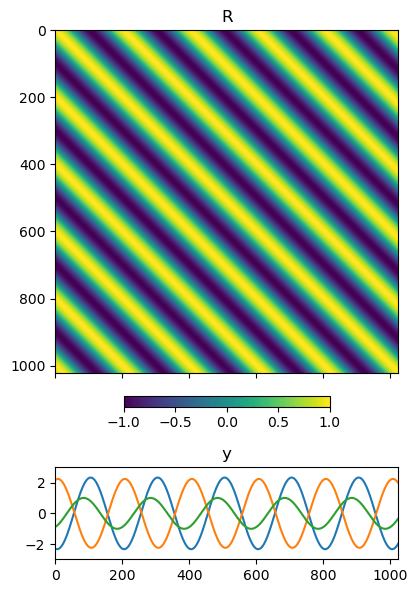
複雑な信号を生成することも出来ます．例えば，適当な音声信号 $\mathbf{y}'$ を準備して，その共分散行列を計算すれば，その音声信号をガウス分布からサンプルすることができます．

\mathbf{R} = \mathbf{y}' \mathbf{y}'^{\mathsf{H}} + \epsilon \mathbf{I}

ただし $\epsilon \in \mathbb{R}_+$ は， $\mathbf{R}$ を正定値にするための微小な正数です．これも実際にサンプルしてみます．まず， $\mathbf{y}'$ として次の音声信号を準備しました．

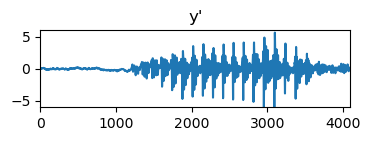
この信号から実際に $\mathbf{R}$ を計算し， $\mathbf{y}$ をサンプルしてみた結果が以下です．ちゃんと音声信号の時間波形が生成出来ていますね．

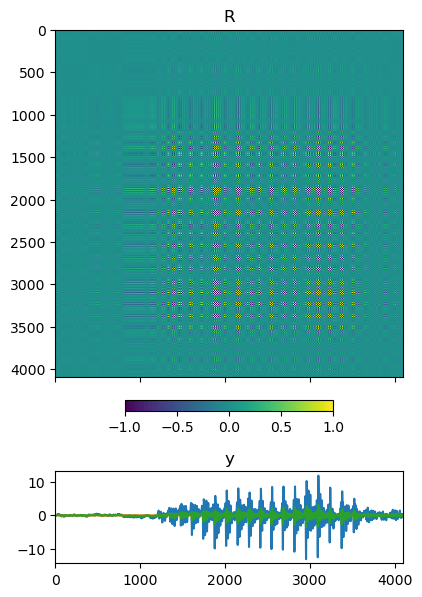
この図では分かり辛いですが， $\mathbf{R}$ のランクは(ほぼ)1なので，もとの信号の形状をそのまま再現出来ています．ただし，自由度が1残っているので，元の信号 $\mathbf{y}'$ を適当な実数でスケールさせた信号が生成されます．

このように，ガウス過程 (or 共分散行列) を用いることで，任意の時間波形を (スケール不定性を許せば) 表現することができます．

Wiener Filtering is All You Need

ガウス過程による時間波形の生成モデルにはスケールの不定性がありますが，実用上は問題になりません．モノラル音源分離を例に説明してみたいと思います．ここでは，観測信号 $\mathbf{y}$ が $K$ 個の音源信号 $\mathbf{y}^{(k)} \in \mathbb{R}^N$ ( $k=1,\ldots,K$ ) の和で表現されると仮定します．

\mathbf{y} = \sum_{k=1}^K \mathbf{y}^{(k)}

さらに，各音源信号は共分散パラメータ $\mathbf{R}^{(k)}$ を持つガウス分布に従っていると仮定します．このとき混合音 $\mathbf{y}$ は，ガウス分布の再生性により，共分散 $\mathbf{R} \triangleq \sum_{k=1}^K \mathbf{R}^{(k)}$ を持つガウス分布に従います．

\mathbf{y} \sim \mathcal{N}\left(\mathbf{0}, \mathbf{R}\right)

音源分離問題は，適当な制約のもと混合音 $\mathbf{y}$ から共分散パラメータ $\mathbf{R}^{(k)}$ を推定する問題として定式化できます．次節で詳しく説明しますが，IS-div.に基づく音源分離もこの枠組みの特殊形と見なすことができます．

共分散パラメータが適当な推論方法で得られたとき，音源 $k$ の推定値 $\hat{\mathbf{y}}^{(k)}$ は， $\mathbf{R}^{(1,\ldots, K)}$ と $\mathbf{y}$ から計算される $\mathbf{y}^{(k)}$ の事後期待値として，以下のように得られます．

\hat{\mathbf{y}}^{(k)} = \mathbb{E}[\mathbf{y}^{(k)} \mid \mathbf{y}, \mathbf{R}^{(1, \ldots, K)}] = \mathbf{R}^{(k)}\mathbf{R} ^{-1} \mathbf{y}

このような分離法はWiener filtering [A. Liutkus+ 2011] と呼ばれています．この式はスカラのアナロジーで考えると分かりやすいですが，半正定値対称行列を用いた観測信号のマスキング (分配) になっているので，分離音のスケールは観測信号 $\mathbf{y}$ を用いて一意に決定できます．

実際に，次のような音声信号 $\mathbf{y}^{(1)}$ と $\mathbf{y}^{(2)}$ の混合音 $\mathbf{y}$ から，音源信号 $\hat{\mathbf{y}}^{(1)}$ と $\hat{\mathbf{y}}^{(2)}$ を復元してみたいと思います．

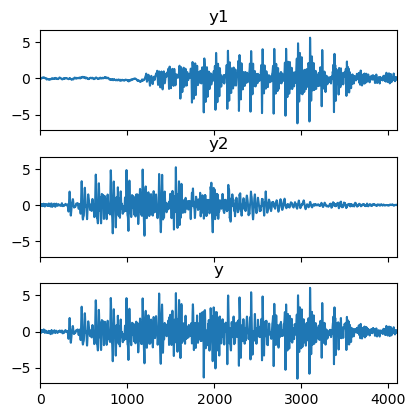
今回は理想的な条件として，正解の音源信号から $\mathbf{R}^{(1)}$ と $\mathbf{R}^{(2)}$ を計算してWiener filteringしてみました．以下の図に，正解信号を左列・分離結果を右列に示します． $\mathbf{R}^{(1, 2)}$ と $\mathbf{y}$ のみから，個別の音源をそのスケールまで正しく復元できていることが分かります．

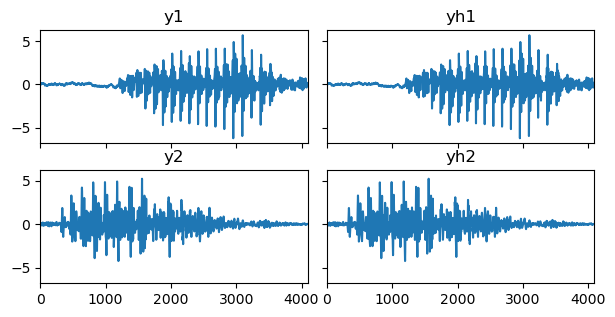
このように，混合音に含まれる音源信号の共分散行列さえ何とかして推定できれば，音源信号を精緻に復元できるようになります．言い換えれば，ある時刻における具体的な値が分からなくても，その期待的な分散と他の時刻との関係性さえ分かっていれば，元の信号を一意に復元できます．筆者も所属している理研 AIP 音響情景理解チームでは，このような時間波形のガウス過程とWiener filteringに基づく深層音源分離をWASPAA 2023 [A. A. Nugraha+ 2023] にて発表しているので，よければ読んでみて下さい．

時間波形の周波数表現

では次に，時間波形の生成モデルを周波数領域で考えてみたいと思います．時間波形 $\mathbf{y}$ に，離散フーリエ変換行列 $\mathbf{F} \in \mathbb{C}^{N\times N}$ を乗ずれば，その周波数表現 $\mathbf{x} \triangleq \mathbf{F}\mathbf{y} \in \mathbb{C}^N$ が得られます．このとき，もとの時間波形 $\mathbf{y}$ が共分散行列 $\mathbf{R}$ を持つ零平均複素ガウス分布に従っていれば，その周波数表現 $\mathbf{x}$ が従う分布は，以下のような零平均複素ガウス分布になります．

\mathbf{F}\mathbf{y} = \mathbf{x} \sim \mathcal{N}_\mathbb{C}\left(\mathbf{0}, \mathbf{F} \mathbf{R} \mathbf{F}^\mathsf{H}\right)

時間波形が複素信号になってしまっていますが，Wiener filteringする場合は，時間表現と周波数表現で結果が一致するので，実用上は問題になりません．

これも，実際にサンプルして眺めてみたいと思います．前々節の最後に登場した音声信号の $\mathbf{R}$ から $\mathbf{Q} \triangleq \mathbf{FRF}^\mathsf{H}$ を計算してみました．

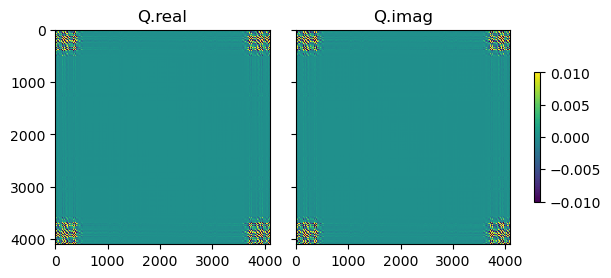
この分布からサンプルしてきた信号を逆離散フーリエ変換すると，下記のような時間信号が得られます．

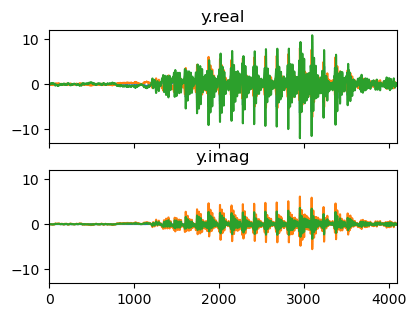
共分散行列 $\mathbf{R}$ (同じく $\mathbf{Q}$ ) のランクが (ほぼ) 1のとき，サンプルした信号は，もとの時間波形を複素数のスカラ倍したような信号になります．この辺は，時間波形での議論を複素数に素直に拡張した話ですね．

板倉斎藤ダイバージェンス

音源分離などのパラメータ推定問題において，共分散行列 $\mathbf{R}$ または $\mathbf{Q}$ を推定するとき，どちらかがよりシンプルな形で書けると，推定問題が楽になると予想されます．多くの (時間・) 周波数領域での音源分離は， $\mathbf{R}$ が離散フーリエ変換行列により対角化されると仮定します．

\mathbf{Q} = \mathbf{FRF}^\mathsf{H} \approx \mathrm{diag}(\mathbf{q})

ここで， $\mathbf{q} \in \mathbb{R}_+^N$ は，対角成分を表す非負ベクトルです．このような仮定がいつ成り立つかといえば，時間波形の共分散 $\mathbf{R}$ が巡回行列の場合です．イメージ的には，信号が定常かつ周波数成分間に相関がない (= 位相を無視する) 場合，このような仮定が成り立ちます．

音響信号処理で短時間フーリエ変換 (STFT) がよく用いられるのは，微小な時間フレームの中では信号が定常と見なせて，この対角化近似が使えるためと捉えることもできます．以降では， $t$ 番目の時間フレームにおける時間信号を $\mathbf{y}_t$ とし，その周波数表現を $\mathbf{x}_{t} \triangleq [x_{t1}, \ldots, x_{tf}, \ldots, x_{tN}]^\mathsf{T}$ として説明を進めます． $\mathbf{x}_t$ の共分散の対角成分 $\mathbf{q}_t$ を $[\lambda_{t1}, \ldots, \lambda_{tN}]^\mathsf{T} \in \mathbb{R}_+^N$ と表すと，これまでの議論から，スペクトログラム $x_{tf} \in \mathbb{C}$ は，以下のような零平均複素ガウス分布に従っていると書くことができます．

x_{tf} \sim \mathcal{N}_\mathbb{C}(0, \lambda_{tf}) =\exp\left(-\log \lambda_{tf} - \frac{|x_{tf}|^2}{\lambda_{tf}}\right)

このガウス尤度は，パワースペクトログラム $|x_{tf}|^2$ とパワースペクトル密度 (PSD) $\lambda_{tf}$ との板倉斎藤ダイバージェンス [C. Févotte+ 2009] に一致しています．共分散行列で厄介だった行列計算がスカラ計算になるので，このようなPSDの推定が近似問題として広く解かれています．逆に，周波数ビン間の相関 (=一種の位相情報) を陽にモデル化した研究としては，半正定値テンソル因子分解 (PSDTF) [K. Yoshii+ 2013] が知られています．

周波数領域での瞬時混合モデル

さて，ここまでLGMが何のモデルかを説明していませんでしたが，LGMは多チャネル音響信号の生成モデルです．多チャネル音響信号というのは，場所の異なる複数のマイク $m=1,\ldots,M$ で収集した信号です．このようなマイクの束はマイクアレイと呼ばれます．音源の位置によってマイク間で音量差や時間差が生じるため，これらの空間情報を用いることで，音源位置や音源信号を推定することができます．

時間差や音量差というのは，時間領域で伝達関数 $\mathbf{b}_m \in \mathbb{R}^N$ を音源信号 $\mathbf{y}_{t}$ に畳み込むことに対応します．

\mathbf{y}_{mt} = \mathbf{b}_m * \mathbf{y}_{t}

ここで， $\mathbf{y}_{mt} \in \mathbb{R}^N$ は $m$ 本目のマイクによる観測信号を表し， $*$ は畳み込み演算を表します．伝達関数の長さが十分短いとき (残響が短いとき)，この畳み込みは時間・周波数領域において，伝達関数の周波数表現 $\mathbf{a}_{f} \in \mathbb{C}^M$ をモノラルの音源信号 $x_{tf}$ へ乗じることに対応します．

\mathbf{x}_{tf} = \mathbf{a}_f x_{tf}

ここで， $\mathbf{x}_{tf} \in \mathbb{C}^M$ は $M$ チャネル観測スペクトログラムを表します．音源信号がPSD $\lambda_{tf}$ を持つ零平均複素ガウス分布に従うとき， $M$ チャネル観測信号 $\mathbf{x}_{tf}$ は，以下の多変量複素ガウス分布に従います．

\mathbf{x}_{tf} \sim \mathcal{N}_\mathbb{C}\left(\mathbf{0}, \lambda_{tf} \mathbf{a}_f \mathbf{a}_f^\mathsf{H} \right)

このような音の伝達モデルは，ランク1空間モデルと呼ばれ，安定かつ高速に推論できるため広く活用されています．ランク1空間モデルを用いた音源分離法の代表例は，独立低ランク行列分析 (ILRMA) [D. Kitamura+ 2016] です．ILRMAは，BSSと呼ばれる手法の一種で，音源信号と伝達過程を統計的に同時推定するため，音源・マイクの位置情報や事前の教師あり学習が不要です．OSSとして実装も公開されているので，マイクアレイを購入すれば，手軽に試すことができます．

局所ガウスモデル

ランク1空間モデルは時不変の伝達関数の畳み込みに基づくため，音源が移動してしまうと性能が劣化します．この問題を緩和するモデルとしてLGM [N. Q. K. Duong+ 2011] が知られています．LGMでは，一つの音源を表すために複数の伝達関数 $\mathbf{a}_{lf} \in \mathbb{C}^M$ ( $l=1,\ldots, L$ ) を用いていると解釈できます．各伝達関数に従う音源信号の足し合わせが観測信号であると解釈すると，観測信号は以下のような多変量複素ガウス分布に従います．

\mathbf{x}_{tf} \sim \mathcal{N}_\mathbb{C}\left(\mathbf{0}, \lambda_{tf} \mathbf{H}_f \right)

ここで $\mathbf{H}_f \triangleq \sum_{l=1}^L \mathbf{a}_{lf}\mathbf{a}_{lf}^\mathsf{H}$ は，伝達関数を足し合わせたフルランク空間相関行列を表します．やっと表題のLGMにたどり着くことができました．実際には，各時刻で特定の1方向からしか音源が到来しない場合でも，移動する音源 = 長期的に見れば複数の方向から到来している音源として解釈できます．音源が大きく移動する場合はこのモデルでも許容できませんが，話者の頭の動きの程度であれば，高い性能を発揮することが知られています．また，喧騒のようなガヤガヤした雑音は，拡散性雑音と呼ばれ無数の方向から音が聞こえていると解釈できますが，このような雑音源の表現にもこのモデルは効果的です．

筆者は，LGMと変分オートエンコーダ (VAE) を組み合わせることで，教師なしで音源分離を学習する深層フルランク空間相関分析 (Neural FCA) という手法を作っています [Y. Bando+ 2021]．この手法とVAEについては，下記の解説記事を書いているので，良ければこちらも読んでください．

LGMとそのBSSへの応用であるFCA [N. Q. K. Duong+ 2011] や多チャネル非負値行列因子分解 (MNMF) [H. Sawada+ 2013] は，ピーク性能は良好な一方，提案された当初は膨大な計算量から現実的な時間内での推論が困難なうえ，初期値依存性が強い課題も知られていました．しかし，近年のGPGPUや償却推論に基づくNeural FCAによって，現実的な推論時間と高い性能を達成できるようになっています．今後，このような深層学習と統計的信号処理を融合した研究がより広く活発に議論されることを期待しています．

おわりに

局所ガウスモデル (LGM) を説明するために，時間波形の生成モデルから順を追って解説してみました．複素信号になるあたりで自分も誤解していた点が明らかになるなど，とても勉強になりました．まだ解説や理解が甘い部分も沢山あるので，疑問点や間違いがあれば気軽に指摘して頂ければと思います．Advent Calendarとしては6日遅れですが，土日のティータイムのお供などとして楽しんで貰えればと思います．本記事の図を生成するために使用したJupyter Notebookは下記から閲覧できます．

また，筆者が所属する産総研社会知能研究チームでは，短期 (・長期) インターンの募集をしています．統計的信号処理と深層学習を融合した研究や，視聴覚統合処理などの研究を推進していますので，ご興味ある方はお気軽にご連絡下さい．

謝辞

本記事の執筆にあたって，沢山の有意義なコメントを頂いた錦見亮博士に感謝いたします．また，修士課程から現在まで，本記事の内容を理解するための沢山の指導を下さった吉井和佳准教授に感謝いたします．