https://arxiv.org/abs/1312.6114
出来るだけ正確かつお手軽にVAEを理解するために書きました.殆どの記事が画像向けに書かれているので,音声向けに書いてみました.音響信号処理に慣れていると読みやすいと思います.
詳しく知りたいひとは,
- 原典を読んでください.一番エッセンスが詰まってるけど,PRMLのVBを先に読んでおこう.
- 須山さんのベイズ深層学習本も良い本だと思います.
VAEとは?
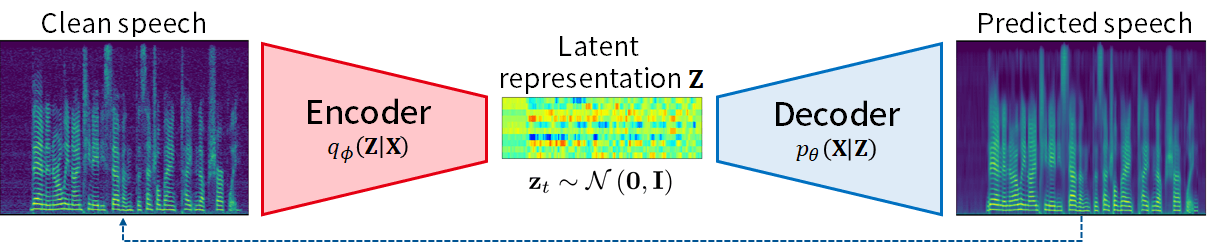
音声信号におけるVAE ([Bando+ 2018]より引用・改変)
深層生成モデル (デコーダ) とその推論モデル (エンコーダ) を一挙に学習する枠組みです.一見オートエンコーダの亜種に見えますが,生成モデルとその推論ととらえた方が応用が広がります.
生成モデル
VAEではまず,観測 (observation) \mathbf{X}の生成過程を記述する,確率的な生成モデル (probabilistic generative model) を仮定します.\mathbf{X}は実数でも複素数でも離散変数でも構いません.VAEはフレームワークなので,データの種類に合わせて適切な生成モデルを仮定すれば良いだけです.
例として,音声信号 \mathbf{X} \triangleq \{x_{ft} \in \mathbb{C}\}_{f,t=1}^{F,T}の生成過程 [Bando+ 2018] を考えます.VAEでは,ある信号\mathbf{X}の特徴を表すD次元の潜在ベクトル列 \mathbf{Z} \in \{\mathbf{z}_t \in \mathbb{R}^D \}_{t=1}^T を仮定します.潜在ベクトル (latent vector, latent representation, latent feature) の各次元は,ピッチや包絡・音素といった音声の特徴を表していると”みなし”ます.ただし,具体的な形態は陽に仮定しません.また,ベクトル列として定義しましたが,スペクトログラム\mathbf{X}全体を1本のベクトルとして表現しても良いです.ともあれ,観測\mathbf{X}が低次元の埋め込み\mathbf{Z}から生成されると仮定します.
統計的音響信号処理では,ゼロ平均複素ガウス分布を用いた生成モデルが簡便で高い性能を達成することが知られています.これを活用して生成モデルを立てると以下のようになります.
x_{ft} \mid \mathbf{z}_t \sim \mathcal{N}_\mathbb{C}\left(0, g_{\theta,f}(\mathbf{z}_t)\right)
ここで,g_{\theta,f}: \mathbb{R}^D\rightarrow\mathbb{R}_+は,潜在変数を観測x_{ft}のパワースペクトル密度 (分散) に変換する,パラメータ\thetaを持つ非線形写像 (つまりDNN) です.これで,p_\theta(\mathbf{X}\mid\mathbf{Z}) という\mathbf{X}の生成過程を定義できました.
VAEでは,この生成モデルのパラメータ\thetaを確率的に尤もらしくなるように学習します.ただし,p_\theta(\mathbf{X}\mid\mathbf{Z}) だけだと,\mathbf{Z}を具体的に与えないと\thetaを学習できないので困ります (\mathbf{X}と\mathbf{Z}の組を使った学習は教師あり学習).そこで,\mathbf{Z}にも分布を置いて,\mathbf{Z}を周辺化することを考えます.この分布はなんでも良いですが,扱いが楽なのでとりあえず標準ガウス分布を置きます.
\mathbf{z}_t \sim \mathcal{N}(\mathbf{0}, \mathbf{I})
ガウス分布以外には,von-Mises Fisher分布[Xu+ 2018]やDirichlet分布[Joo+ 2020]などが提案されています.潜在変数の事前分布を置いたことで,同時分布p_\theta(\mathbf{X}, \mathbf{Z}) = p_\theta(\mathbf{X}\mid \mathbf{Z})p(\mathbf{Z})が定義でき,\mathbf{Z}を周辺化できます.
p_\theta(\mathbf{X}) = \int p_\theta(\mathbf{X}, \mathbf{Z}) d\mathbf{Z}
これで,\thetaさえ決まれば,観測\mathbf{X}を生成する分布が求まります.言い換えれば,ある\thetaの尤もらしさを観測\mathbf{X}のみから測れるようになりました.このような分布を周辺尤度と言います.
推論
VAEの学習では,訓練データ\{ \mathbf{X}^{(1)}, \ldots, \mathbf{X}^{(N)}\}に対する対数周辺尤度を最大化するように\thetaを最適化します.
\argmax_{\theta} \sum_{n=1}^N \log p_\theta\left( \mathbf{X}^{(n)} \right)
以降,\sumの内側に注目して議論するので,{}^{(n)}は省略します.対数周辺尤度を最大化する上で最大の問題点は,非線形関数gの積分を含むことで,特殊な制約を置かないと計算できません.
この問題を解決するために,VAEでは変分EM (variational expectation-maximization) 法を用います.対数周辺尤度は,以下のようにJensen不等式によって下限を取ることができます.
\begin{aligned}
\log p_\theta(\mathbf{X}) &= \log \int p_\theta(\mathbf{X}, \mathbf{Z}) d\mathbf{Z} \\
&\geq \int q(\mathbf{Z}) \log \frac{p_\theta(\mathbf{X}, \mathbf{Z})}{q(\mathbf{Z})}d\mathbf{Z} \\
&= \int q(\mathbf{Z}) \log p_\theta(\mathbf{X} \mid \mathbf{Z})d\mathbf{Z} - \int q(\mathbf{Z}) \log \frac{q(\mathbf{Z})}{p(\mathbf{Z})}d\mathbf{Z} \\
&= \mathbb{E}_q[ \log p_\theta(\mathbf{X} \mid \mathbf{Z}) ] - \mathcal{D}_\mathrm{KL}[q(\mathbf{Z}) \mid p(\mathbf{Z})] \triangleq \mathcal{L}
\end{aligned}
ここで,q(\mathbf{Z})は非負かつ積分して1になる"補助変数 (関数)”です.q(\mathbf{Z})がどんな値をとっても1行目 -> 2行目の不等式は成立し,q(\mathbf{Z})がp_\theta(\mathbf{Z}\mid \mathbf{X})と一致するときにのみ等号が成立します.変分EMでは,1行目の対数周辺尤度を直接最大化する代わりに,変形結果の変分下限 \mathcal{L} (ELBO; evidence lower bound) を最大化するように,\thetaとq(\mathbf{Z})を交互に更新します.下限を最大化しても,対数周辺尤度が最大になるわけではないんですが,極大値には到達できます.後述するように,変分下限は効率的に(近似) 計算できるので,対数周辺尤度が直接計算できない問題を (強引に) 解決できました.厳密には,\thetaとq(\mathbf{Z})は勾配法を用いて同時に更新するのでEMではないですが,理解には役立ちます.

対数周辺尤度と変分下限の関係 (PRML Fig. 9.14より引用).Mステップでパラメータを更新 (θold → θnew) し,Eステップでqを更新 (青 → 緑) する.
ここまで{}^{(n)}は省いていましたが,q(\mathbf{Z}^{(n)}) は訓練データの個々のサンプルで最適値が異なる上に,最適化には複数回の更新が必要なので,膨大な空間・時間計算量が必要になります.この問題を解決するために,VAEでは償却変分推論 (AVI; amortized variational inference) [Gershman+ 2014] [Zhang+ 2018] というアイディアを活用します.このアイディアは今日の深層学習では割と一般的ですが,「各サンプルに対応するq(\mathbf{Z}^{(n)})を覚えておく」のではなく,「あるサンプル\mathbf{X}^{(n)}に対するq(\mathbf{Z}^{(n)})を出力するDNN q_\phi(\mathbf{Z}\mid\mathbf{X})を学習」します.全サンプル覚えず写像を最適化するので空間計算量を削減でき,あるサンプルで更新したq_\phi(\mathbf{Z}\mid\mathbf{X})は他のサンプルにもその知見が転用できるので,時間計算量も削減できます.q_\phi(\mathbf{Z}\mid\mathbf{X})は,例えば次のような形を取ります.
\begin{aligned}
q_\phi(\mathbf{Z}\mid\mathbf{X}) &\triangleq \prod_{t,d} q_\phi(z_{td} \mid\mathbf{X}) \\
&=\prod_{t,d} \mathcal{N}\left(\mu_{\phi,d}(\mathbf{x}_t), \sigma^2_{\phi,d}(\mathbf{x}_t)\right)
\end{aligned}
ここで,\mu_{\phi,d}: \mathbb{C}^F \rightarrow \mathbb{R} と \sigma^2_{\phi,d}: \mathbb{C}^F \rightarrow \mathbb{R}_+ はそれぞれ,観測\mathbf{X}から潜在変数の事後分布の平均・分散パラメータを出力するDNNです.このDNNはエンコーダや推論モデル (inference model)と呼ばれます.
推論モデルを導入して,変分下限を書き直すと以下のようになります.
\mathcal{L} = \mathbb{E}_{q_\phi}[ \log p_\theta(\mathbf{X} \mid \mathbf{Z}) ] - \mathcal{D}_\mathrm{KL}[q_\phi(\mathbf{Z}\mid \mathbf{X}) \mid p(\mathbf{Z})]
お気持ち的な解釈をすると,第一項はエンコーダ→デコーダを通して出てきた再構成値が観測に近づくように,第二項はエンコーダの出力が事前分布から大きく離れないように学習します.
第二項のKLダイバージェンスは,要素間に相関のないqと標準ガウス分布pのダイバージェンスなので,解析的に以下のように計算できます.
\mathcal{D}_\mathrm{KL}[q_\phi(\mathbf{Z}\mid \mathbf{X}) \mid p(\mathbf{Z})] = \sum_{t,d} \frac{1}{2} \left\{ \left( \mu_{\phi,d}(\mathbf{x}_t)\right)^2 + \sigma_{\phi,d}^2(\mathbf{x}_t) -\log \sigma_{\phi,d}^2(\mathbf{x}_t) \right\}
第一項の期待値計算は,直接計算できないので,サンプル近似します.
\mathbb{E}_{q_\phi}[ \log p_\theta(\mathbf{X} \mid \mathbf{Z}) ] \approx -\sum_{f,t} \left\{ \log g_{\theta,f}(\mathbf{z}^*_t) + \frac{1}{g_{\theta,f}(\mathbf{z}^*_t)}|x_{ft}|^2\right\}
ここで,\mathbf{z}^*_t は,q_\phi(\mathbf{Z}\mid\mathbf{X}) からサンプルした値で,PyTorchだとtorch.distributions以下の分布クラスの rsampleメソッドを使えば,微分可能な形でサンプルを得られます.原典では再パラメータ化トリック (reparametarization trick) っていうのが提案されてますが,本質ではないので割愛.qからのサンプルが無限個あれば,期待値と一致しますが,VAEでは”動くので”1個のサンプルで近似します.これでやっと,変分下限が微分可能な形で計算できたので,あとは確率的勾配法を用いて最適化すればよいです.このような,解析的に求まらない変分事後分布を勾配法を用いて推定する枠組みを,black box variational inference (BBVI) [Ranganath+ 2014] と呼びます.
深層生成モデルやAVIを用いた応用
深層フルランク空間相関分析法

深層フルランク空間相関分析法の概要 ([Bando+ 2021] より引用)
宣伝です.この研究では,複数の音が混じった混合音から個別の信号を抽出する音源分離について,VAEを活用して教師なしかつ高性能な枠組みを実現しました.
https://ybando.jp/projects/spl2021
深層音源分離は高い性能を発揮できるため注目を集めていますが,大量の混合音と音源信号のペアデータが必要で学習コストが高い課題がありました[Luo+ 2019].一方,音の空間的な伝播(物理)モデルを活用すれば教師なしで音源分離できますが,精緻なモデルは推論が難しく性能に限界がありました[Sekiguchi+ 2022].そこでこの研究では,後者で用いられる確率モデルを非線形化 (深層生成モデル化) してデコーダとし,これを効率よく推論する (AVIする) エンコーダと一体で学習することで教師なし音源分離を実現します.つまり,深層学習と統計的信号処理の良いとこ取りができるわけです.簡単な解説はこちら.



Discussion