薄明方程式をきちんと解く

地球上の夜の領域をGeoJSON化するにおいて、

$k$が0以外のときはニュートン法やはさみうち法で求めることになる。

としたが、それだとうまくいかないケースに遭遇したので、解き方を見直す。

薄明方程式の再掲

$$f = \sin(\delta) \sin(\phi) + \cos(\delta) \cos(\phi) \cos(t) - \sin(k) = 0$$

$\delta$は太陽の赤緯で、境界線を求める時刻により決まる。
$\phi$は境界線上の点の緯度。
$t$は境界線上の点の時角で、経度によりで決まる。
$k$は太陽の出没高度で、夜側に光がどれくらい回り込むかを決める変数。

この方程式を、経度を-180degから180degまで変化させながら緯度$\phi$を計算することで、昼と夜の境界線を求めることができる。

k=0のとき

$k=0$ のときは式変形すると、

$$\phi = \arctan(-\cos(t) / \arctan(\delta))$$

となり解析解が求まる。

なお、$\delta=0$ のとき薄明方程式は　$\cos(\phi) \cos(t) = 0$　となり、$\phi=0$ に定まる^[1]。

それ以外

$k$が0以外のときは、ニュートン法やはさみうち法で求めることになる。 としていたが、数値解析ではうまくいかない場合がある。

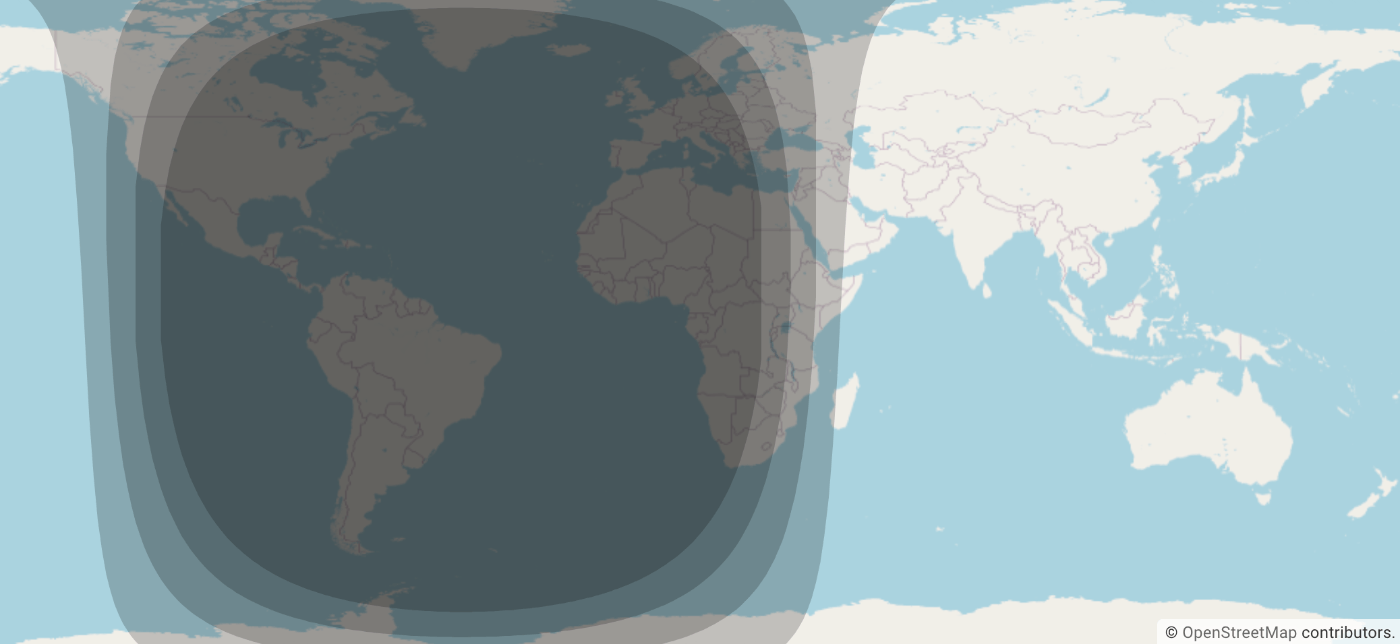
例えばこういうときで、影の領域が円を描く＝1つの経度に対して解が2つある。

数値解析の代わりに $\sin(\phi)$ か $\cos(\phi)$ を $x$ として $a x^2 + b x + c = 0$ の二次方程式の解を求める。
$-90deg <= \phi <= 90deg$ なことから^[2] $x = \sin(\phi)$ 、 $\sqrt{1 - x^2} = \cos(\phi)$ とすれば、薄明方程式は次の形になる。

$$\cos(\delta) \cos(t) \sqrt{1 - x^2} = - \sin(\delta) x + \sin(k)$$

よって、$A = cos(\delta) \cos(t)$、$B = -sin(\delta)$、$C = sin(k)$、$D = A^2 + B^2 - C^2$ とすれば

$$x = (-B * C \pm A * \sqrt{D}) / (A^2 + B^2)$$

となる。
ただし、$\delta\neq\pm90deg$($A\neq0$) かつ $(B x + C) / A > 0$ を満たすものとする^[3]。

なお、$\delta=\pm90deg$($A=0$) のときは、 $x = -C / B$ となる。

他の考慮点

影の領域が円を描く場合は、180度線をまたぐ際に分割されるため、PolygonではなくMultiPolygonを求めるようにする。

高度$k$ は厳密には大気屈折 $E = 0.035\degree \sqrt{H}$ と 視差 $\Pi = 0.0024\degree / r$ を考慮する必要がある。
市民薄明の例

$$k = -6\degree - E + \Pi$$

しかし大気屈折は高度$H$の関数で、高度を考慮しない場合は0となる。
視差は地球と太陽の距離の天文単位$r$の関数だが、ほぼ1であり視差は十分に小さいものであり、考慮しないでよいケースがほとんどだろう。

https://github.com/yonda-yonda/geo4326/blob/master/src/terminator.ts

脚注

1. 厳密には $t=\pm90deg$ のときに解が求まらないが、求めたい点の経度をわずかにずらせば$t$の値も0からずれるため、ここでは目をつむる($t=\pm90deg$ とならないものとする)。

2. Math.asin()は -pi/2 から pi/2の値を返すので、緯度と範囲が一致する。Math.acos()は 0 から piの値を返す。

3. 厳密には $t=\pm90deg$ のときも $A=0$ となり解が求まらないが、ここでは$k=0$ のとき同様 $t=\pm90deg$ とならないものとする。