Zenn
🌎

地球上の夜の領域をGeoJSON化する

2023/10/01に公開
GeoJSON
tech

その時刻の夜（または昼）の領域を世界地図上に表示したくなる瞬間が人生にはある。

この昼夜の境界線を英語ではTerminatorという[1]。

境界線の座標は幾何学的に求めることができる。
計算方法は日の出・日の入りの計算―天体の出没時刻の求め方に詳しい[2]。

ウェブページではこちらがよくまとまっている。

出没方程式もしくは薄明方程式

f = \sin(\delta) \sin(\phi) + \cos(\delta) \cos(\phi) \cos(t) - \sin(k) = 0

\deltaは太陽の赤緯で、境界線を求める時刻により決まる。
\phiは境界線上の点の緯度。
tは境界線上の点の時角で、経度によりで決まる。
kは太陽の出没高度で、夜側に光がどれくらい回り込むかを決める変数。

太陽が地平線の下に隠れてもしばらく明るい薄明時間というが、
地平線に太陽が隠れた瞬間を求めたければk=0とする（日の出日の入りの同時線）。
なお、k=-6とすれば市民薄明、k=-12とすれば航海薄明、k=-18とすれば天文薄明の範囲を求めることになる[3][4]。

よってkを決めればあとは時刻と境界線上の点の経度から、境界線上の点の緯度を求めることができ、経度を-180degから180degまで[5]で計算していけば、その時刻の境界線を描くことが可能となる。

解析解

k=0のときは式変形すると、

\phi = \arctan(-\cos(t) / \arctan(\delta))

となり解析解が求まる。

数値解

kが0以外のときはニュートン法やはさみうち法で求めることになる。

時角

t = \Theta + longitude - \alpha

\Thetaはグリニッジ恒星時[6]
\alphaは太陽の赤経

参考

太陽の赤経・赤緯

赤経は時角を求めるために必要。

順序としては、

  1. 計算したい日時からユリウス通日を求める
  2. ユリウス通日から太陽の黄経を求める
  3. ユリウス通日から黄道傾斜角を求める
  4. 太陽の黄経と黄道傾斜角から赤経・赤緯を求める

各式は「日の出・日の入りの計算―天体の出没時刻の求め方」やwikipediaを参照のこと。

プログラム

k=0のときに限定した関数

import { Feature, Polygon } from "geojson";

const getJulianDate = (date: Date | number): number => {
    // https://www5d.biglobe.ne.jp/~noocyte/Programming/GregorianAndJulianCalendars.html
    const d = date instanceof Date ? date.getTime() : date;
    return d / 86400000 + 2440587.5;
}

const getGreenwichMeanSiderealTime = (jd: number): number => {
    // https://aa.usno.navy.mil/faq/GAST
    return (18.697374558 + 24.06570982441908 * (jd - 2451545)) % 24;
}

const getSunEclipticLongitude = (jd: number): number => {
    // https://en.wikipedia.org/wiki/Position_of_the_Sun
    const n = jd - 2451545;
    const L = (280.46 + 0.9856474 * n) % 360;
    const g = ((357.528 + 0.9856003 * n) % 360) * Math.PI / 180;

    // radians
    return (L + 1.915 * Math.sin(g) + 0.02 * Math.sin(2 * g)) * Math.PI / 180;
}

const getEclipticObliquity = (jd: number): number => {
    // https://ja.wikipedia.org/wiki/%E9%BB%84%E9%81%93%E5%82%BE%E6%96%9C%E8%A7%92
    const t = (jd - 2451545) / 36525;

    // radians
    return ((84381.406 - 46.836769 * t - 0.00059 * t ** 2 + 0.001813 * t ** 3) / 3600) * Math.PI / 180;
}

const getSunEquatorialPosition = (longitude: number, obliquity: number): number[] => {
    // 日の出・日の入りの計算 天体の出没時刻の求め方 長沢工著 ISBN4-8052-0634-9
    let alpha =
        Math.atan(Math.tan(longitude) * Math.cos(obliquity));
    const delta =
        Math.asin(Math.sin(longitude) * Math.sin(obliquity));

    if (Math.sin(longitude) > 0) {
        if (Math.sin(alpha) < 0) alpha += Math.PI
    } else {
        if (0 < Math.sin(alpha)) alpha += Math.PI
    }

    // radians
    return [alpha, delta];
}

const getLatitude = (longitude: number, alpha: number, delta: number, gmst: number): number => {
    // 日の出・日の入りの計算 天体の出没時刻の求め方 長沢工著 ISBN4-8052-0634-9
    // 太陽高度kを0に固定
    const hourAngle = (gmst * 15 * Math.PI / 180 + longitude) - alpha;
    // radians
    return Math.atan(-Math.cos(hourAngle) / Math.tan(delta));
}

const calculate = (date: Date, division = 360): Feature<Polygon> => {
    const jd = getJulianDate(date);
    const gmst = getGreenwichMeanSiderealTime(jd);

    const sunEclipticLongitude = getSunEclipticLongitude(jd);
    const eclipticObliquity = getEclipticObliquity(jd);
    const [alpha, delta] = getSunEquatorialPosition(sunEclipticLongitude, eclipticObliquity);

    const longlats: number[][] = [];
    const diffDeg = 360 / division;
    for (let longitude = -180; longitude < 180; longitude += diffDeg) {
        const latitude = getLatitude(longitude * Math.PI / 180, alpha, delta, gmst);
        longlats.push([longitude, latitude * 180 / Math.PI]);
    }
    const latitude = getLatitude(Math.PI, alpha, delta, gmst);
    longlats.push([180, latitude * 180 / Math.PI]);

    if (delta > 0) {
        longlats.push([180, -90]);
        longlats.push([-180, -90]);
        longlats.push(longlats[0]);
        longlats.reverse();
    } else {
        longlats.push([180, 90]);
        longlats.push([-180, 90]);
        longlats.push(longlats[0]);
    }

    return {
        type: "Feature",
        properties: {
            "datetime": date.toISOString()
        },
        geometry: {
            type: "Polygon",
            coordinates: [longlats]
        }
    }
}

GeoJSONのPolygonはcounterclockwiseである必要があるので南半球側に陰があるときはlonglats.reverse();している

2023-10-01T07:00:00Zごろのポリゴンをgeojson.ioで表示してみた様子

脚注

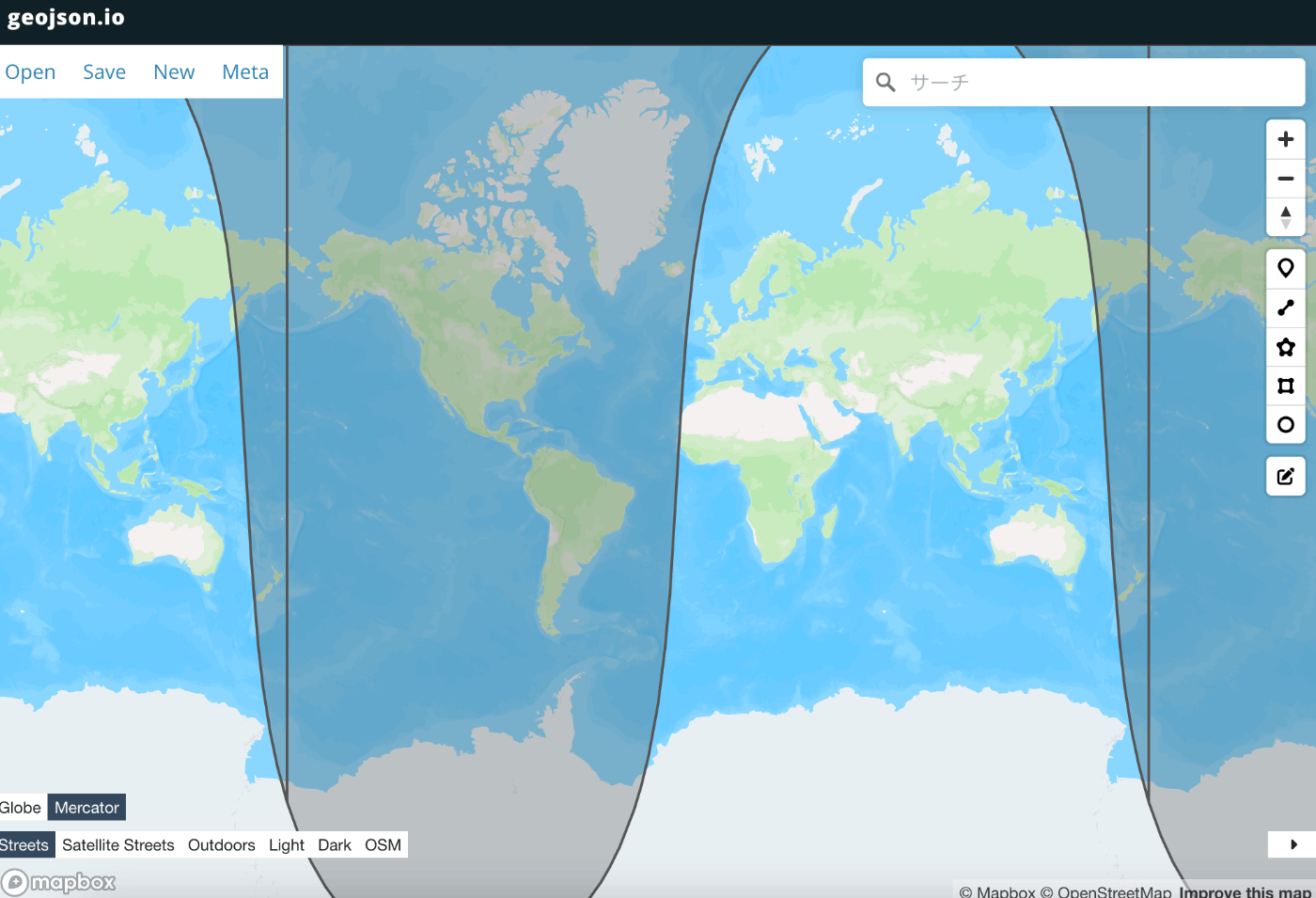
  1. 検索時は某映画と区別がつくよう「terminator day night line」などと言葉を足すとよい。 ↩︎

  2. 長沢工先生の本はすべて良著で、これだけの内容を日本語で学べることに感謝しきりである。 ↩︎

  3. 薄明時間の分類は世界的にはこの三種類が一般的で、k=-6は一等星が見えだす限界の明るさ、k=-12は航海中に水平線が見える限界の明るさ、k=-18は六等星が見えだす限界の明るさということらしい。 ↩︎

  4. 本来は線上の地点の標高や視差も方程式に含まれるが、ここではどちらも0としている。 ↩︎

  5. 「日の出・日の入りの計算―天体の出没時刻の求め方」のP58では緯度を2deg刻みで計算すれば十分とされている。 ↩︎

  6. 長沢本ではグリニッジ視恒星時だが、プログラムではグリニッジ平均恒星時を求める式を利用している。両者の差は1秒もないので今回の計算では十分な精度である。 ↩︎

Discussion