【ベクトル・行列】機械学習で使う数学をいまさら勉強する【図解あり】

Webエンジニアとして7年、これまで機械学習とは無縁でしたが、手札を増やすべくディープラーニングの勉強を始めました！

「機械学習で使う数学をいまさら勉強する」シリーズでは、「ロジスティック回帰モデル」および「ニューラルネットワーク」の理解を目標にします。

本シリーズで目指す目標

本記事は微分に続き、第2回として「ベクトル・行列」をまとめます。

• 公開済み : 【微分】機械学習で使う数学をいまさら勉強する
• ⭐️ 本記事：【ベクトル・行列】機械学習で使う数学をいまさら勉強する
• 未公開：【指数関数・対数関数】機械学習で使う数学をいまさら勉強する
• 未公開：【多変数関数の微分】機械学習で使う数学をいまさら勉強する
• 未公開：【確率・統計】機械学習で使う数学をいまさら勉強する

🤖 機械学習になぜ数学の知識が必要なのか？

まず、機械学習モデルの役割について確認しておきましょう。

• 機械学習モデルは、入力データを受け取って、それに対応する出力データを返す関数のようなもの
• そして、その関数の振る舞いは、データから学習することで決定される

この関係を、数学の概念と結びつけて考えてみましょう。

下の図は、手書きの郵便番号を識別する機械学習モデルの例です。

手書きの「5」という画像を入力として与えると、数字の「5」という予測結果が出力されます。

ここで、機械学習モデルに入力を与える際、定量データに変換してあげる必要があります。機械学習モデルは人間のように目で判断できないので情報を数字にする必要があるのです。

このように、「定性的なデータを定量的なデータに変換する」という作業に数学的な知識が役立ちます。また、もちろん、変換されたデータを使って機械学習モデルそのものを作る過程でも、数学は不可欠です。

どのような数学が使われるかについては、後ほど詳しく説明します。

ベクトル・行列と機械学習

次に、機械学習においてベクトルと行列がどのように関係するか？を説明します。

ディープラーニングの一種であるニューラルネットワークでは、複数の入力データに対してそれぞれ重みを付けて、複数の結果を出力します。

重み（W） は、入力データそれぞれの重要度を調整する数値です。例えば、明日の天気を予測する場合、「現在の空の色」よりも「現在の気圧」の方が重要な情報になりそうですよね。このように、情報の重要度を重みとして数値で表現します。

ここから数学的な話になっていきます。
例として2つの入力と3つの出力を扱うシンプルなニューラルネットワークを考えてみましょう。

各出力の結果は、次のような式で計算されます。

$y_1 = w_{11}x_1 + w_{12}x_2$
$y_2 = w_{21}x_1 + w_{22}x_2$
$y_3 = w_{31}x_1 + w_{32}x_2$

この程度の式であれば計算は可能ですが、
入力の数と出力の数が10個になったら？100個だったら？？

だいぶ面倒ですよね。

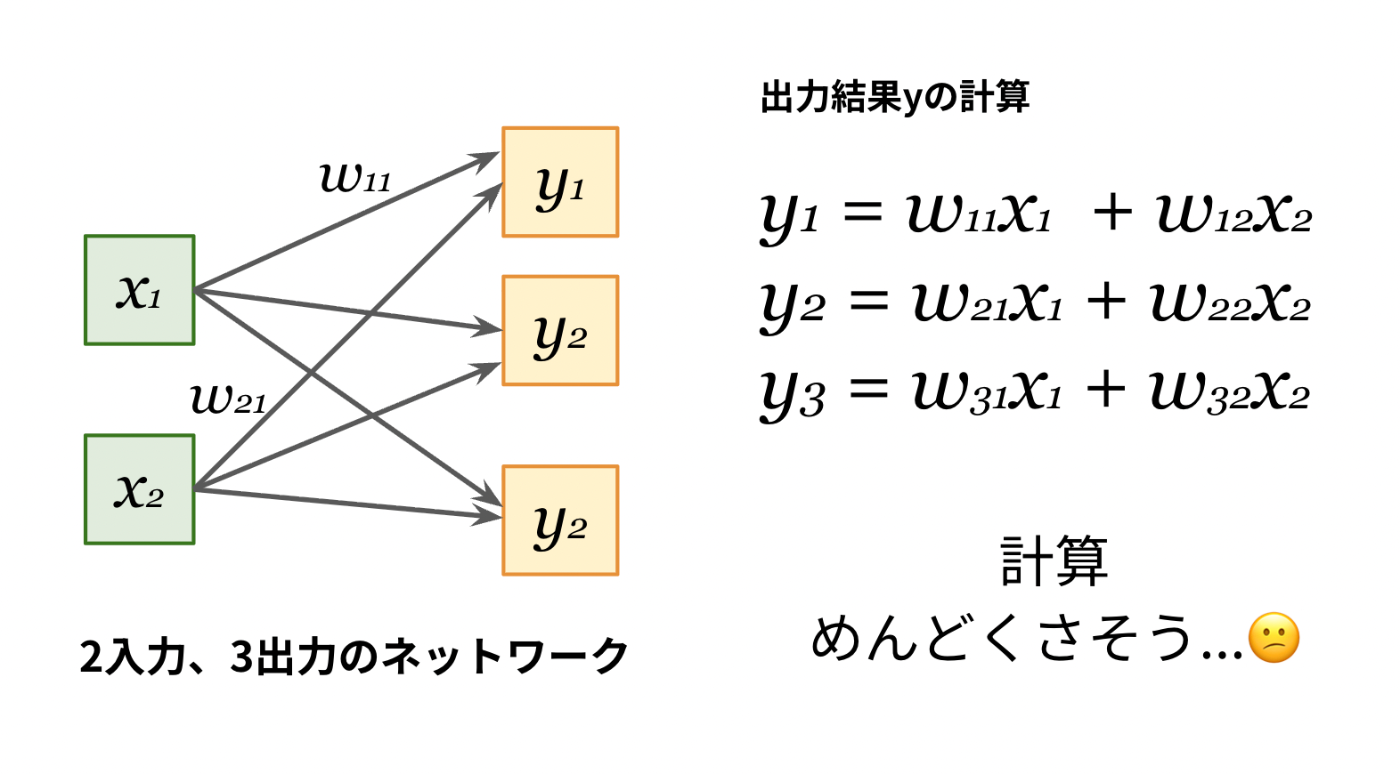
しかし、ここでベクトルと行列を用いることで、この計算を次のように表現できます。

$y = Wx$

急にすごくシンプルになりましたね!
このように、ニューラルネットワークの計算をなるべく楽〜にするために、ベクトル・行列を使用します。

ベクトルとは？

ベクトルとは、数を縦か横に並べたものです。
小難しく考えず、データのかたまりなんだな〜とイメージすればOKです。

ベクトルはアルファベットの小文字に矢印を乗せたものや、太字で表現されます。
以下はベクトルの表記例です。

矢印を使ったベクトルの表現

$$\begin{aligned} \vec{a} &= \left( \begin{array}{c} 1 \\ 2 \\ 3 \end{array} \right) \quad & \vec{b} &= \begin{pmatrix} 9 , 0.25 , -5 , 41 \end{pmatrix} \end{aligned}$$

太字を使ったベクトルの表現

$$\begin{aligned} \mathbf{p} &= \left( \begin{array}{c} p_1 \\ p_2 \\ \vdots \\ p_m \end{array} \right) \quad & \mathbf{q} &= \begin{pmatrix} q_1 , q_2 & \cdots , q_n \end{pmatrix} \end{aligned}$$

なお、行ベクトルでも列ベクトルでも、表記の仕方が違うだけで中身は同じです。
適宜見やすい方を選択します。

ベクトルと次元の関係

ベクトルとは、複数の値をひとまとまりにしたデータそのもののことです。そして、そのベクトルに含まれる要素の数が次元と呼ばれます。

たとえば、3つの値からなるベクトルは3次元ベクトル、n個の値からなるベクトルはn次元ベクトルとなります。

• ベクトル: データを構成する値の並び（例: $[25, 10, 65]$）
• 次元: ベクトルを構成する要素の数（例: 3次元）

次元のイメージ

次元のイメージについて、もうすこし解説します。

高校でベクトルを「2次元の矢印」として習った方もいるかもしれません。矢印も間違いではないですが、機械学習における次元は「独立した異なる要素の数」と考えるのがより適切です。

たとえば、ある人物の情報をデータとして表現する場合を考えてみましょう。

• 1次元: 身長のみ（170cm）→「平均的な身長の人だな〜」
• 2次元: 身長と体重（170cm, 60kg）→「細身の人だな〜」
• 3次元: 身長、体重、年齢（170cm, 60kg, 18歳）→「細身の若者だな〜」

このように、身長、体重、年齢はそれぞれが独立した要素です。要素の数、つまり次元が増えるほど、その人物の特徴をより詳細に把握できます。

この考え方は機械学習にも当てはまります。データの次元が高いほど、モデルは対象の特徴をより正確に捉えやすくなり、結果として精度の向上が期待できます。

次元を増やしすぎると「次元の呪い」と呼ばれる問題が発生することがあります。
が、一般的には、要素が多い方が精度が高くなる傾向にあります。

✅　ベクトルに関する数学の公式

ベクトル・行列の単元では「内積」「コサイン類似性」が重要ワードです。

ここからは機械学習で主に使う公式をずらずらと並べます。
証明は省略します。

ベクトルの和

2つのベクトルを足し合わせると、各成分同士を足し合わせた新しいベクトルになります。

$$\mathbf{a} + \mathbf{b} = \begin{pmatrix} a_1 \\ a_2 \\ \vdots \\ a_n \end{pmatrix} + \begin{pmatrix} b_1 \\ b_2 \\ \vdots \\ b_n \end{pmatrix} = \begin{pmatrix} a_1 + b_1 \\ a_2 + b_2 \\ \vdots \\ a_n + b_n \end{pmatrix}$$

計算してみよう

具体的な例として、2次元のベクトルの和を計算してみましょう。

ベクトル $\mathbf{a} = (1, 2)$ とベクトル $\mathbf{b} = (3, -1)$ の和を求めます。

$$\mathbf{a} + \mathbf{b} = \begin{pmatrix} 1 \\ 2 \end{pmatrix} + \begin{pmatrix} 3 \\ -1 \end{pmatrix} = \begin{pmatrix} 1 + 3 \\ 2 + (-1) \end{pmatrix} = \begin{pmatrix} 4 \\ 1 \end{pmatrix}$$

ベクトルの差

引き算も同様に、各成分同士を引きます。

$$\mathbf{a} - \mathbf{b} = \begin{pmatrix} a_1 - b_1 \\ a_2 - b_2 \\ \vdots \\ a_n - b_n \end{pmatrix}$$

計算してみよう

2次元でのベクトルの差を計算してみましょう。

ベクトル $\mathbf{a} = (1, 2)$ と ベクトル $\mathbf{b} = (3, -1)$ の差を求めます。

$$\mathbf{a} - \mathbf{b} = \begin{pmatrix} 1 \\ 2 \end{pmatrix} - \begin{pmatrix} 3 \\ -1 \end{pmatrix} = \begin{pmatrix} 1 - 3 \\ 2 - (-1) \end{pmatrix} = \begin{pmatrix} -2 \\ 3 \end{pmatrix}$$

よって、$\mathbf{a} - \mathbf{b} = (-2, 3)$ となります。

ベクトルのスカラー倍

本記事では、ベクトルの積としてスカラー倍と内積を紹介します。
先に、イメージしやすいスカラー倍を説明します。

スカラーというとかっこいい感じですが、ただの実数のことです。

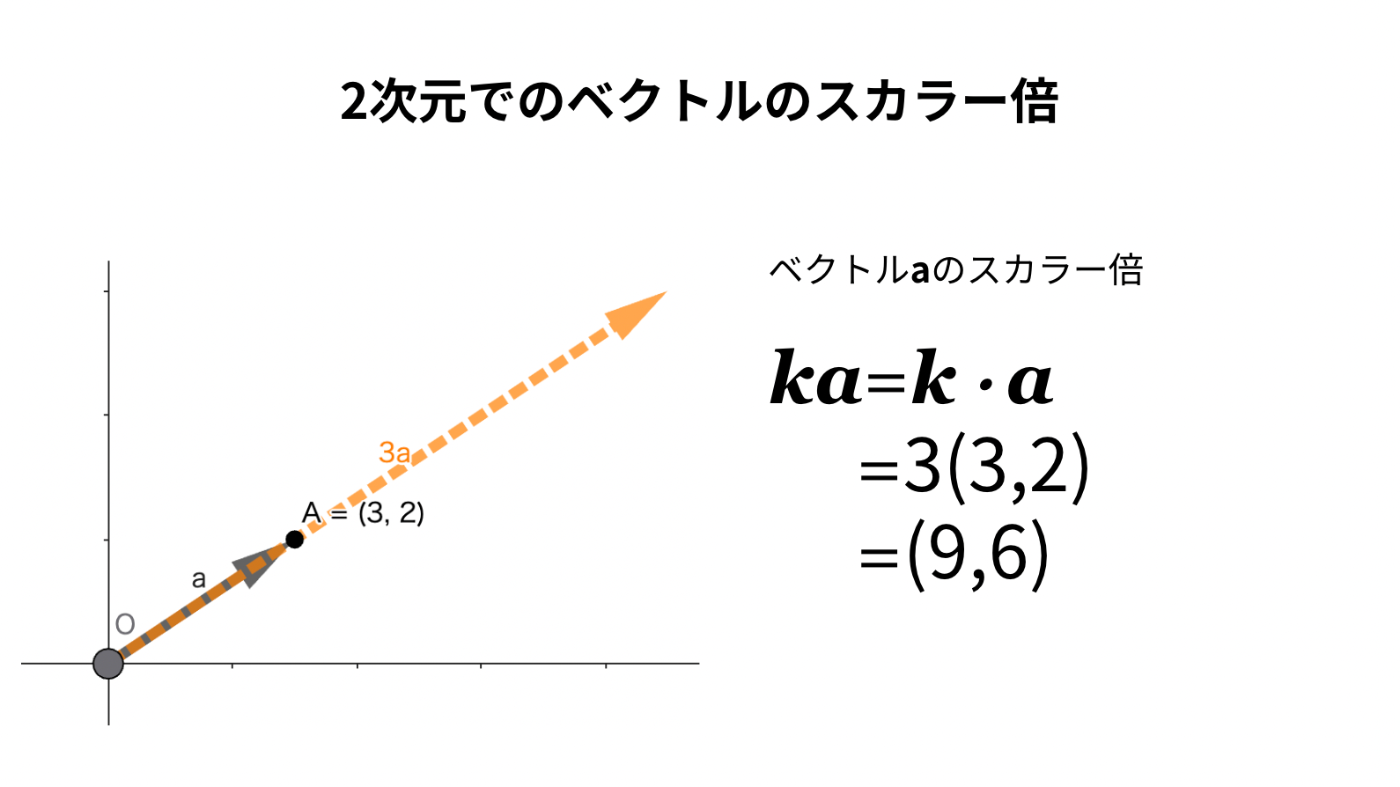
ベクトルにスカラーを掛けると、各成分がその数倍になります。

$$k\mathbf{a} = k \cdot \begin{pmatrix} a_1 \\ a_2 \\ \vdots \\ a_n \end{pmatrix} = \begin{pmatrix} k a_1 \\ k a_2 \\ \vdots \\ k a_n \end{pmatrix}$$

計算してみよう

スカラー $k=3$ をかけると、

$$\begin{aligned} k\mathbf{a} &= k\cdot (a_x,\; a_y) \\ &= 3(3,2) \\ &= (9,6) \end{aligned}$$

ベクトルの長さ（絶対値）

ベクトルの大きさ（長さ）は、絶対値記号を使って次のように表します。

$$|\mathbf{a}| = \sqrt{a_1^2 + a_2^2 + \cdots + a_n^2}$$

計算してみよう

2次元のベクトルの場合、三平方の定理で絶対値を求めることができます。

$$\mathbf{a} = (3,4) \quad \Rightarrow \quad |\mathbf{a}| = \sqrt{3^2+4^2}=5$$

ここではわかりやすさのために「絶対値記号」を使っていますが、
機械学習では ノルム(||） という表記を使う方が一般的です。

ベクトルの内積（絶対値）

内積はベクトル同士の「方向の近さ」を表します。

$$\mathbf{a}\cdot\mathbf{b} = |\mathbf{a}||\mathbf{b}|\cos\theta$$

求め方

急にcosθが出てきてなんじゃ？！と思うかもしれないですが、図にするとわかりやすいです。

まず、三角比の定義を思い出してください。$\cos\theta$は直角三角形の斜面を底辺で割った値でしたね。

$$x = r\cos\theta$$

では内積をもとめてみましょう。
内積はベクトル同士の積です。まず、はじめに、ベクトルの方向を合わせます。
なんで方向をあわせるかというと、その方が計算しやすいからです。

$$bと同じ方向のベクトル = a\cdot\cos\theta$$

そして、スカラー倍と同じ要領で、ベクトルの積を求めると、

$$\mathbf{a}\cdot\mathbf{b} = |\mathbf{a}|\cos\theta \cdot |\mathbf{b}|$$

となります。

ベクトルの内積（成分）

内積はベクトル同士の積の一種ですが、次のように定義されます。

$$\begin{aligned} \mathbf{a} & = (a_1, a_2, \cdots, a_n) \\ \mathbf{b} & = (b_1, b_2, \cdots, b_n) \end{aligned}$$

のとき、

$$\begin{aligned} \mathbf{a}\cdot\mathbf{b} & = (a_1, a_2, \cdots, a_n)\cdot(b_1, b_2, \cdots, b_n) \\ & = (a_1b_1+a_2b_2+\cdots+a_nb_n) \\ & = \sum_{k=1}^n a_kb_k \end{aligned}$$

内積をとる際は、2つのベクトルの要素数（次元）が同じである必要があります。

計算してみよう

ベクトルaとベクトルbの内積を求めてみます。

$$\begin{aligned} \mathbf{a} & = (1, 0) \\ \mathbf{b} & = (3, 2) \\ \mathbf{a}\cdot\mathbf{b} & = 1*3 + 0*2= 3 \end{aligned}$$

ちなみに、Pythonのnumpyを使えば一瞬で計算できます。

import numpy as np

a = np.array([1, 0])
b = np.array([3, 2])

# ベクトルaとbの内積
print(np.dot(a, b))  # 3

⭐️【重要】コサイン類似度

コサイン類似度とは、2つのベクトルが「どのくらい似ているか」を表す尺度です。

$$\cos(\theta) = \frac{\mathbf{a}\cdot\mathbf{b}}{|\mathbf{a}||\mathbf{b}|}$$

コサイン類似度はベクトルの向きを比較して類似度を図るため、大きさは関係ありません。
２つのベクトルのなす角で表現されます。

１に近いほど２つの要素は似ており、０に近づくほど似ていないことを表します。

コサイン類似度	角度	ベクトルの向き	類似度
1	0度	同じ向き	完全に似ている
0	90度	直交	無関係
-1	180度	反対向き	完全に似ていない

どんなところで使われている？

コサイン類似度は機械学習のさまざまなツールに取り入れられている考え方で、その一つにWord2vecがあります。
Word2vecは、分散表現を使って、単語をベクトルに変換し、単語間の類似度を数値化するツールです。

「分散表現」とは単語同士の関連性や類似度に基づくベクトルで単語を表現することです。

Word2vecでは、単語の分散表現を得るために、CBOW（Continuous Bag-of-Words）かSkip-gramのニューラルネットワークモデルのいずれかが使われます。

ちなみに、Word2vecの「2」は数字の2ではなく、英語の「to」を意味し、「WordからVectorへ」という変換プロセスを表しています。

また、Word2vecを拡張したツールとして、doc2vecがあります。これは、単語だけでなく文章全体の類似度をベクトルで表現するツールです。

✅ 行列に関する数学の公式

行列の和・差

行列の加減算は「同じ位置の要素同士」を足したり引いたりします。

$$A + B = \begin{pmatrix} a_{11} & a_{12} \\ a_{21} & a_{22} \end{pmatrix} + \begin{pmatrix} b_{11} & b_{12} \\ b_{21} & b_{22} \end{pmatrix} = \begin{pmatrix} a_{11}+b_{11} & a_{12}+b_{12} \\ a_{21}+b_{21} & a_{22}+b_{22} \end{pmatrix}$$

行列のスカラー倍

行列全体に数を掛けると、すべての要素がその数倍になります。

$$cA = c \cdot \begin{pmatrix} a_{11} & a_{12} \\ a_{21} & a_{22} \end{pmatrix} = \begin{pmatrix} c a_{11} & c a_{12} \\ c a_{21} & c a_{22} \end{pmatrix}$$

⭐️【重要】行列の内積

行列の内積は計算にひと癖ありますが、やり方を覚えればそこまで難しくはありません。

具体的な式を見てみましょう。

$$W= \begin{pmatrix} 2 & -1 \\ 0 & 3 \\ 1 & 4 \end{pmatrix}, \quad x= \begin{pmatrix} 5 \\ -2 \end{pmatrix} \quad\Rightarrow\quad y=Wx= \begin{pmatrix} 2\cdot5+(-1)\cdot(-2) \\ 0\cdot5+3\cdot(-2) \\ 1\cdot5+4\cdot(-2) \end{pmatrix} = \begin{pmatrix} 12 \\ -6 \\ -3 \end{pmatrix}$$

計算の前提条件

行列の積を計算するには、「左の行列の列数」と「右の行列の行数」が一致している必要があります。

求め方

行列の計算は左側の行と右側の列を要素ごとに掛けて足します。

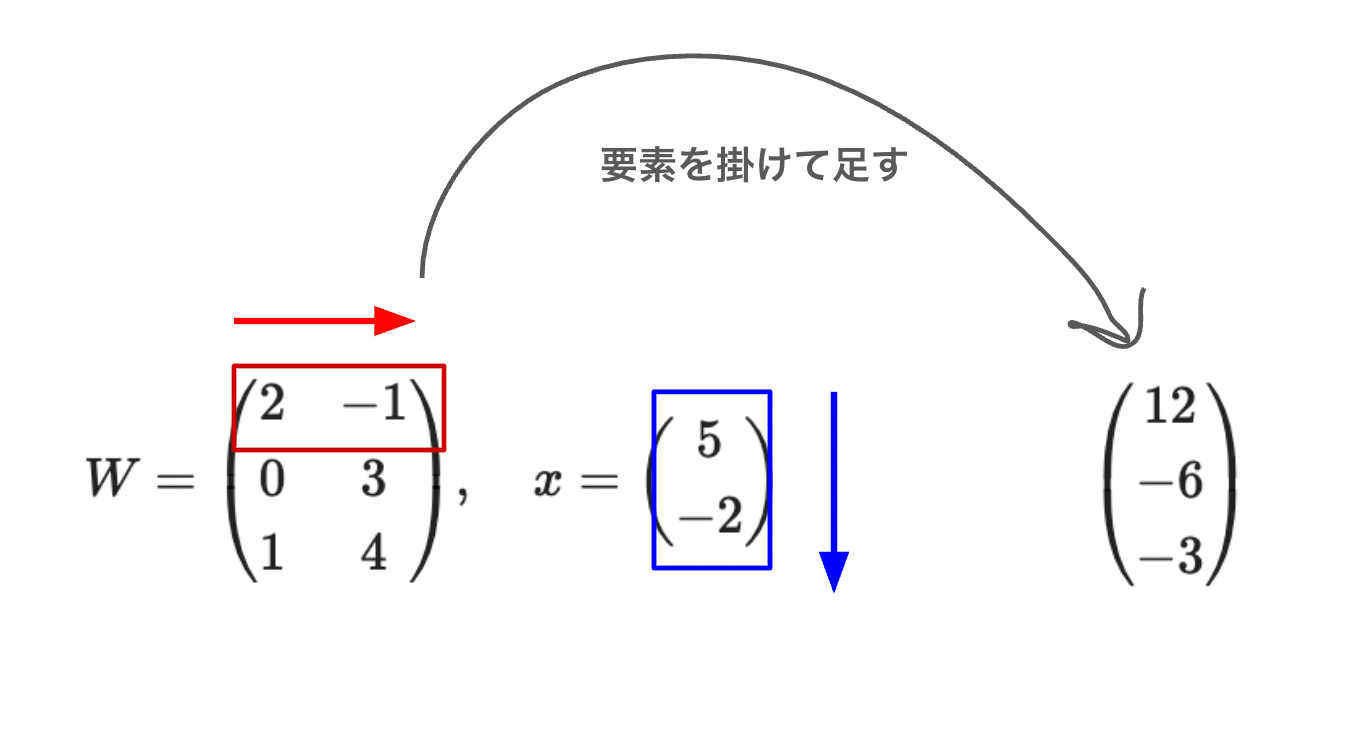
ちなみに、ベクトルの内積と同様に、PythonのNumpyを使えば一瞬で計算できます。

import numpy as np

# 重み行列W
W = np.array([[1, 2], 
              [3, 4], 
              [5, 6]])

# 入力ベクトルx
x = np.array([10, 20])

# 行列の積を計算
y = np.dot(W, x)

print(y) # [ 50  110  170]

おわりに

今回は、機械学習を学ぶ上で必要なベクトル・行列の基本的な考え方とよく使う公式をまとめました。
次回は「指数関数・対数関数」を紹介します。
お楽しみに！

学習に利用する参考資料

主に赤石 雅典氏の著書「『最短コースでわかる ディープラーニングの数学』」を元に学習を進めます。

『最短コースでわかる ディープラーニングの数学』

書籍の詳細
https://bookplus.nikkei.com/atcl/catalog/19/273470/

コサイン類似度（Cosine Similarity）とは？
https://atmarkit.itmedia.co.jp/ait/articles/2112/08/news020.html

自然言語処理とチャットボット: AIによる文章生成と会話エンジン開発
https://www.udemy.com/course/ai-nlp-bot/?couponCode=MT250908JP