🤖

【微分】機械学習で使う数学をいまさら勉強する【図解あり】

に公開
AI
ディープラーニング
機械学習
微分
tech

Webエンジニアとして7年、これまで機械学習とは無縁でしたが、手札を増やすべくディープラーニングの勉強を始めました！

高校以来10年以上ぶりの数学で、眠くなりながら学んでおります（笑）
ここでは、その学習過程を記録していきます。

数学の知識はゆとり教育の高校生レベルですので、温かい目でお気づきの点があればコメントくださいませ。

🤖 機械学習になぜ数学の知識が必要なのか？

はじめに、機械学習モデルとはなにか？の定義を確認します。

  • 機械学習の定義
    • 機械学習モデルとは入力データに対して出力データを返す関数のような振る舞いをもつ
    • 機械学習モデルの振る舞いは、学習により規定される

次の図は、スーパーの売上げ予測モデルのイメージです。

入力として「気温」「天気」パラメーターを入力とし、機械学習モデルに与えます。
学習済みの機械学習モデルは、「アイスがいつもより1.5倍売れそうです。」という予測結果を出力します。

この図における機械学習モデルを作るために、また、より精度の高い結果を出すために、数学の知識が必要なのです。
具体的にどのような数学の知識を使うかは、後ほど記載します。

本シリーズで目指す目標

「機械学習で使う数学をいまさら勉強する」シリーズでは、「ロジスティック回帰モデル」および「ニューラルネットワーク」の理解を目標にします。
本記事は記念すべき第1回です。

  • ⭐️ 本記事 : 【微分】機械学習で使う数学をいまさら勉強する
  • 未公開：【ベクトル・行列】機械学習で使う数学をいまさら勉強する
  • 未公開：【指数関数・対数関数】機械学習で使う数学をいまさら勉強する
  • 未公開：【多変数関数の微分】機械学習で使う数学をいまさら勉強する
  • 未公開：【確率・統計】機械学習で使う数学をいまさら勉強する

微分と機械学習

微分とは？

微分は「小さな変化を見ること」です。
ある点において、次の値は大きくなるのか？小さくなるのか？を予測するためにの傾きを求めます。

数学的な表現をすると、

関数のあるグラフ上の点を中心に、グラフを無限に拡大していくとグラフは限りなく直線に近づく。この時の直線の傾きを微分という。

だそうです。

簡単な例をみてみましょう
y=x^3+2x^2上の、ある点を中心に近づいてみましょう。

遠目から見るとグラフは曲線に見えますが、点を中心に近づくと直線にみえます。
この直線はx軸の値が大きくなるにつれ、y軸の値が減少する、マイナスの傾きを持つ直線に見えます。

このように、グラフを無限に拡大し、限りなく直線に近づけて考えることを極限といいます。

損失関数との関係

機械学習と微分の関係を考えます。

機械学習における、ニューラルネットワークの学習には、微分が使用されます。
これは、損失関数というモデルの予測値と正解値との差を表す関数です。

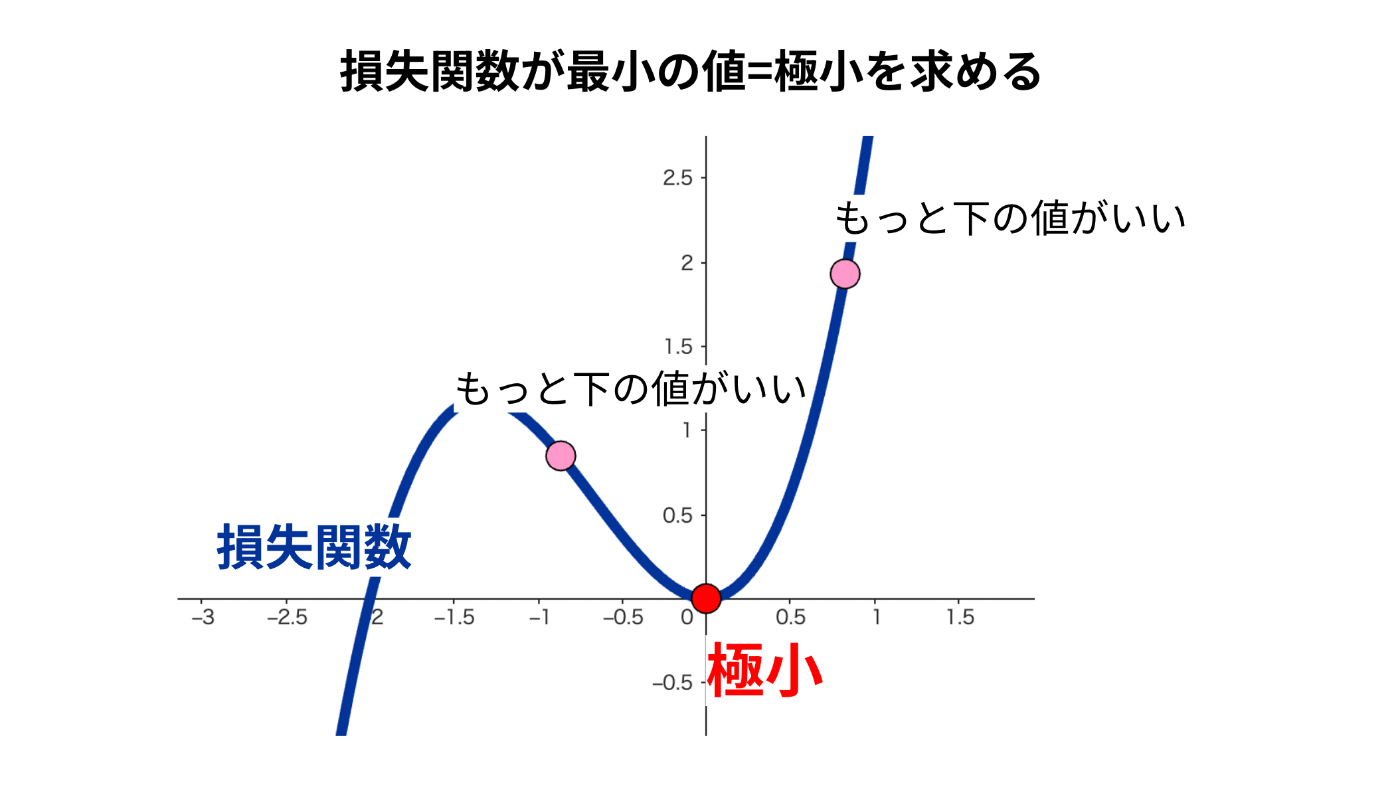
この損失関数は低ければ低いほどよく、最も低い値である極小を知りたいのです。
（予測と正解の差は小さいほうがいいですよね。）

この、極小を求めるために、微分が必要なのです。

✅ 微分に関する数学の公式

機械学習で主に使う公式をずらずらと並べます。
証明は省略します。

合成関数

合成関数とは、簡単に言うと、関数の中に関数を組み込んだもののことです。

\begin{aligned} u & = f(x) \\ y & = g(u) \\ \end{aligned}

のように、複数の関数の合成で表される関数のことです。

  • 関数 f(x) に関数 g(x) を入れる場合、f(g(x)) と表記し、これは (f \circ g)(x) と書きます。
  • 関数 g(x) に関数 f(x) を入れる場合、g(f(x)) と表記し、これは (g \circ f)(x) と書きます。

例で考える

簡単な例で考えてみましょう。

f(x) = x^2、g(x) = 2x のとき、関数 f(x) に関数 g(x) を入れると、合成関数は (f \circ g)(x) となり、以下のようになります。

f(g(x)) = f(2x) = (2x)^2 = 4x^2

一方で、関数 g(x) に、関数 f(x) を入れる場合は、(g \circ f)(x) と表記し、以下のようになります。

g(f(x)) = g(x^2) = 2\cdot x^2 = 2x^2

このように、関数の順番によって結果が異なります。

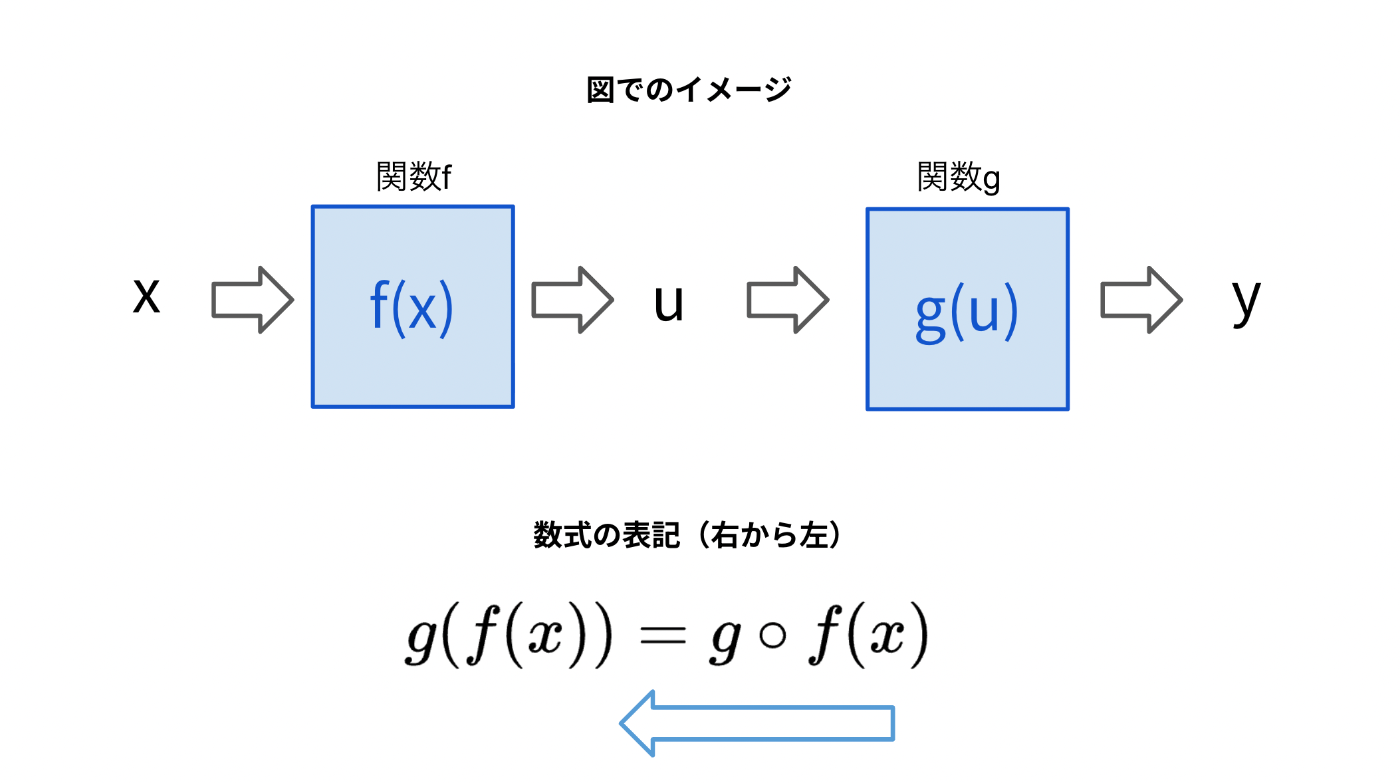
表記の慣習

数学の世界では、右から左へ計算が進むため、関数 g(x) に関数 f(x) を入れる場合、g(f(x))=g \circ f(x) と表記します。

合成関数の微分

合成関数の微分は、構成する各関数の導関数の積で表すことができます。これを連鎖律といいます。
連鎖律は以下の式で表されます。

\frac{dy}{dx} = \frac{dy}{du} \frac{du}{dx}

グラフで理解する

Geogebraより「合成関数の微分」をわかりやすくグラフするとこのようになります。
作成者の方、ありがとうございます！
https://www.geogebra.org/m/drvE5DmN

多項式の微分

多項式とは、f(x)=a_nx^n + a_{n-1}x^{n-1} + \dots + a_1x + a_0 のように、変数と定数を足し算と掛け算で組み合わせた式のことです。

多項式f(x)=nx^nを微分する公式は以下の通りです。

\frac{d}{dx} x^n = nx^{n-1}

ところで微分は線形性という性質をもちます。

線形性とは？

線形性とは、簡単に言えばグラフが直線っぽいということです。

直線っぽいと何がいいかというと、「入力に対する出力の予測が容易」な点です。

図でみてみましょう。
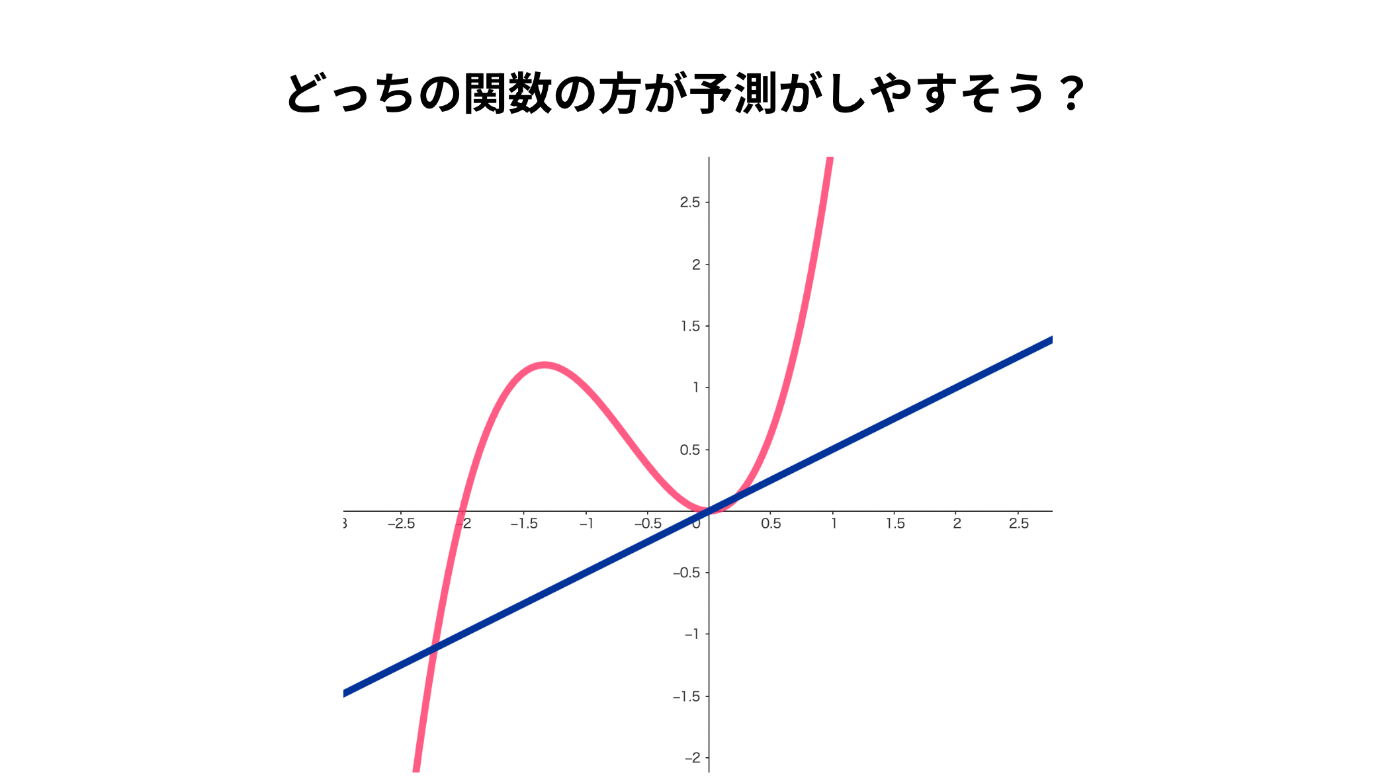
ピンクの関数: y=x^3+2 x^2と青の関数: y=0.5 xだと、どちらの方が、出力の予測がしやすそうでしょうか？

明らかに青の関数の方が簡単に計算できそうですよね。
これが線形性を持つことメリットです。

逆関数の微分

逆関数とは、もとの関数 y=f(x) に対して、x と y を入れ替えた関数 x=g(y) のことです。

逆関数の微分公式は以下のようになります。

\frac{dy}{dx} = \frac{1}{\frac{dx}{dy}}

例で考える

y=x^2 + 1 (x≥0)の逆関数は\sqrt{x-1}です。

ある関数 y=f(x) とその逆関数 y=f^{−1}(x) とでは、
グラフは y=xの直線に関して対称になる という性質をもちます。

接線の方程式

関数 y=f(x) 上の点 (a, f(a)) における接線の方程式は、その点での微分係数 f'(a) を傾きとして、以下のように表されます。

y - f(a) = f'(a)(x-a)

例で考える

曲線 y=0.5x^2 の点 (-2, 2) における接線の方程式は、y=-2x-2 です。

はじめに触れたように、損失関数を最小にする点を求めるためには微分が必要です。
その際、接線の傾きが0となる点を探すことが、極小を求める手がかりになります。

y=0.5x^2 の場合、傾きが0になるのは点 (0,0)です。

積の微分

次は、2つの関数 f(x) と g(x) の積 y = f(x)g(x) を微分する公式です。

\frac{d}{dx} f(x)g(x) = f'(x)g(x) + f(x)g'(x)

商の微分

次は、2つの関数 f(x) と g(x) の商 y = f(x)/g(x) を微分する公式です。

\frac{d}{dx} \frac{f(x)}{g(x)} = \frac{f'(x)g(x) - f(x)g'(x)}{g(x)^2}

積・商の微分はこんな公式あるな〜ってかんじで...。

おわりに

今回は、機械学習を学ぶ上で必要な微分の基本的な考え方とよく使う公式をまとめました。
次回は「ベクトル・行列」を紹介します。
お楽しみに！

学習に利用する参考資料

主に赤石 雅典氏の著書「『最短コースでわかる ディープラーニングの数学』」を元に学習を進めます。

『最短コースでわかる ディープラーニングの数学』

書籍の詳細
https://bookplus.nikkei.com/atcl/catalog/19/273470/

GitHub
https://github.com/makaishi2/math_dl_book_info?tab=readme-ov-file

中学数学からはじめるAI(人工知能)のための数学入門

予備校のノリで学ぶ「大学の数学・物理」というYoutubeチャンネル

https://youtu.be/7A05OamqCyc?si=Gq-YXaQ6JnHMFCBC

AIのための数学講座：少しづつ丁寧に学ぶ人工知能向けの線形代数/確率・統計/微分

Udemy講座「AIのための数学講座：少しづつ丁寧に学ぶ人工知能向けの線形代数/確率・統計/微分」
https://www.udemy.com/course/math-for-ai

GeoGebra

関数をグラフで表現できます。ログインすると、教材集から他の人が作成したグラフを見ることもできます。

https://www.geogebra.org/graphing

参考記事

https://atmarkit.itmedia.co.jp/ait/articles/2009/03/news020.html

https://www.krrk0.com/linearity/

Discussion