シンギュラリティーと汎化
の21日目の記事です。遅れてしまいまして申し訳ありません。また紹介する論文とその位置づけをまだ十分には理解できていません。
では特異学習理論によってディープラーニングにおいて特異性を持つ(ヤコビアンが縮退した)loss関数が重要な役割を示すことを説明しました。
しかし幅の広い事後分布、loss関数のflat minimaを持つことは推定できてもlossの極小値が一つながりのピークになるとは必ずしも言えません。
学習結果のパラメーターが局所最適解に落ちにくいことを説明する異なる観点からの幾つかの試みを紹介します。
特異点の複雑さとモデル選択
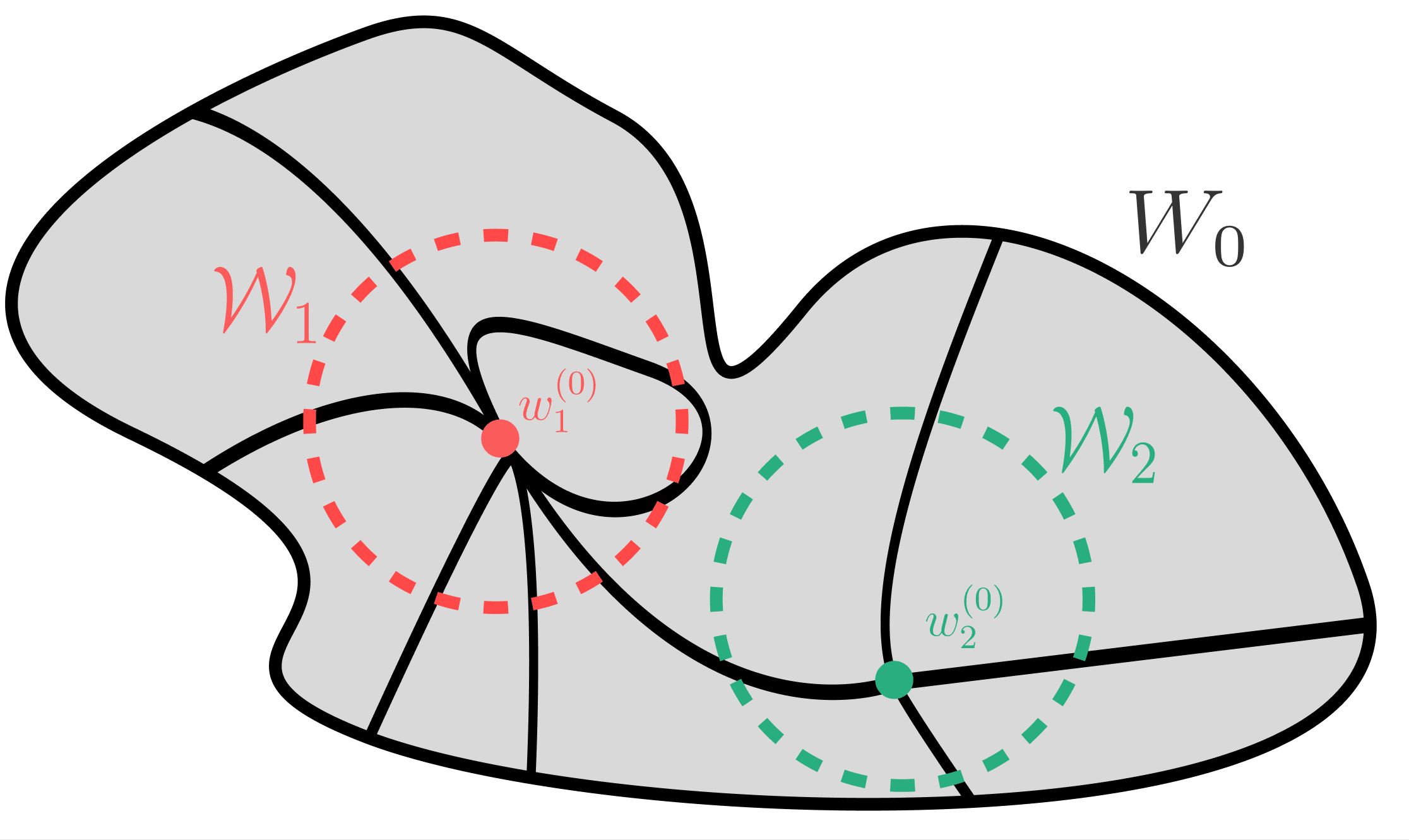
局所的な実対数しきい値(学習係数)λが小さい＝特異性が高い点(図のW1)のほうがが近傍が平らである=事後分布が大きいく選ばれやすいという説明です。一方で「"Algebraic Geometry and Statistical Learning Theory"」ではデータ数が多いほうが特異性の小さい(λの大きい)点が選ばれやすいという記述もあります(238 page)。
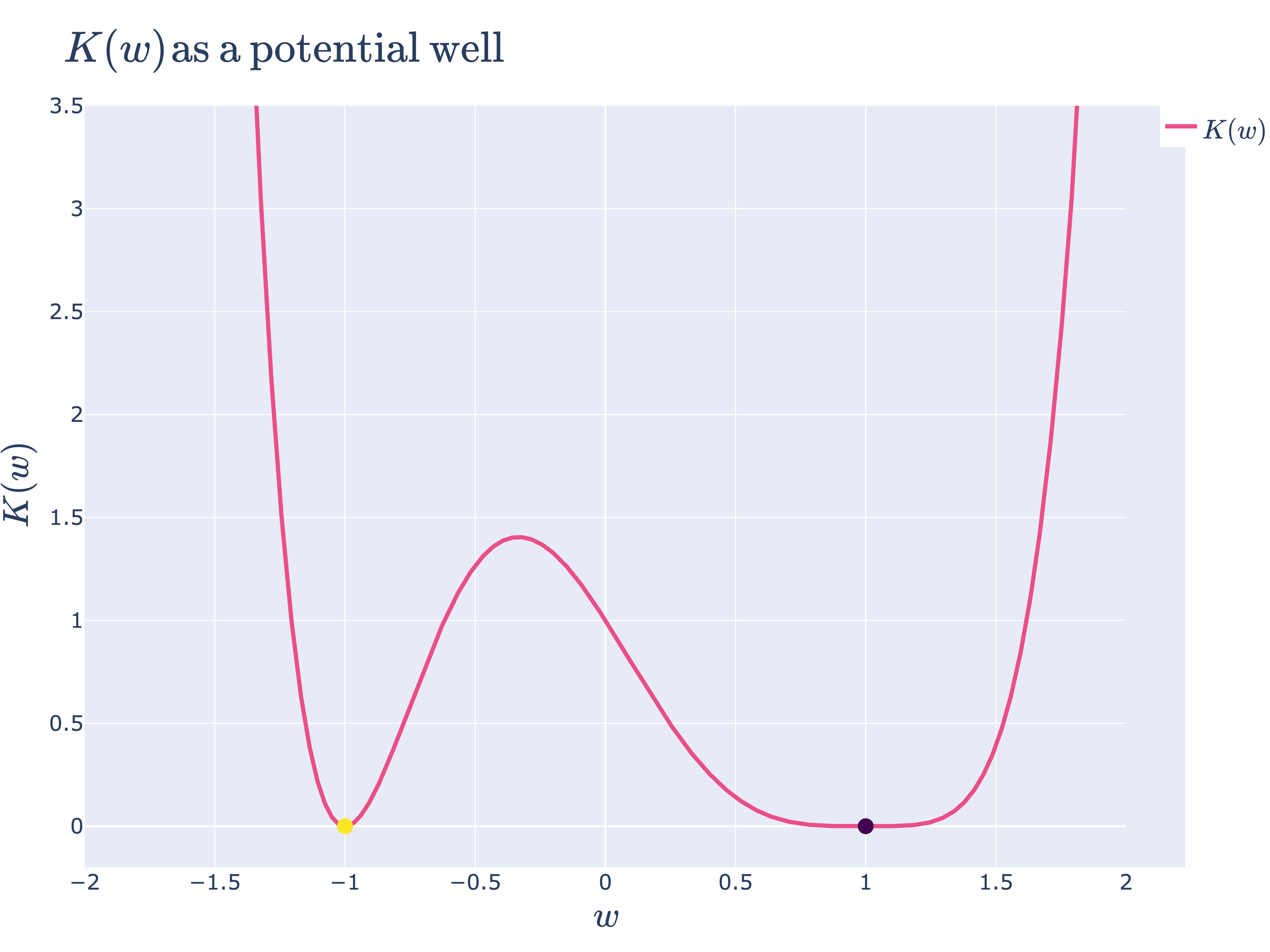
低次元の場合ですが以下の図のように極小値の周辺の自由度(λ)が小さいほど平坦で、面積として表させる事後分布が大きくなります。SGDなどの最適化アルゴリズムでは最終的に選ばれるパラメーターは1点でベイズ的推論はしていませんが、極小値周囲の形状が影響すると言えるかもしれません。しかし異なる極小値のBasinに初期値が位置してしまっていては最適値には到達しないようにも思えます。
ネットワークの対称性と連続変換がflat minimaをつなぐ
ネットワークのもつ対称性とそれを保つような連続変換がflat minimaをつなげているのではないかという主張があります。全結合ニューラルネットは素子の入れ替えに対してloss関数が変わらない自由度を持つ(縮退している)という性質が有りそれを連続的な変換でつなげるというアイデアです。
そのようなモデルは冗長性が有り、圧縮性が高いというPAC Bayes的な見方と整合性があります。
Structural Degeneracy in Neural Networks
簡単なモデルの場合にも現れるdouble descent
データ数に対してモデルのパラメーター数を増やしていくと汎化誤差が一旦は増えるものの徐々に低下していくような関係になることをdouble descentと呼びます。古典的な機械学習ではパラメーターを増やすと過学習し、汎化誤差が下がってしまうはずなのにそうではないところが直感に反しています。
Reconciling modern machine learning practice and the bias-variance trade-ofより引用
最も単純な線型回帰モデルでのdouble descentが見られること、あるいはどのような場合に見られるかについて説明してます。overparametererizedの場合学習される回帰係数
として定義していてラグランジュの未定乗数法を用いてunderparameterizedな場合とは異なる停留値を求めています。
NeurIPS2023でも線型回帰の場合にdouble descentが起きうることの解説が有りました。
比較
以上のように異なるアプローチからDNNが最適解に到達しやすい理由、その周囲でflat minimaを持つ理由が説明されています。
特異学習理論の見方ではニューラルネットのような複雑なモデルではloss関数の極小値の近くは平坦であり、そのような特異性の高い極小の事後分布は大きく、ランダムな初期値からは選ばれやすいことが主張されます。特異学習理論では特異点の性質を見ていますが、"ネットワークの対称性と連続変換がflat minimaをつなぐ"ではネットワークの対称性、冗長性によってつながっている解の軌道(のようなもの)を見ています。特異点はヤコビアンが縮退し特定の方向に対してつながりを持っていると言えますが、無限に近い近傍の話でどことつながってるかについては語られません[1]
これらはモデルを固定した場合の性質についての説明ですが、簡単なモデルの場合にも現れるdouble descentはそれらとは全く異なりパラメーター数を増やしていったときにより汎化誤差が低くなる。そのようなモデルが選択されると主張しています。動かしている量が違うためこれらが同じ大域的な最小解とその周囲の状況を説明しているとは即座には言い切れませんが何らかの関係があるのではないかと思います。
滞りがちですがflat minimaと汎化の説明に関する研究をまとめています。
-
学習軌道を力学系としてみたときの安定多様体との関係も興味深いですが更に話が発散してしまします。 ↩︎
Discussion