「配列のすべての要素が条件を満たすなら True を返す」関数を定義するとき、空の配列を渡したら True を返すべき数学的説明
発端
@fumieval 様のツイート。
空の配列を渡したら True を返すべき
この関数に空の配列を渡したら True を返すべきである。仕様によるとか状況によるとか相談すべきとか例外を返すべきかもといった意見もあるようだが、議論の余地がないレベルで True を返すしかない。最大の理由は
「True を返さないと、空集合があらゆる集合の部分集合になるというルールに矛盾するから」
である。これは数学における集合論の定理のひとつであり、「これを認めないとそれに連なる集合論のすべてが瓦解する」というルールのひとつであって、認めない相応の理由があるとすれば「数学のもっとも基礎的なルールのひとつを覆してでも実現しなければならないことがある」という次元での話になる。
少なくとも私は 10 年以上プログラミングをしていてそんな状況に遭遇したことはない。
【2023/06/01 追記】
数式がわからないという意見がけっこう見られたので『超簡単な説明』を追記しました。数式よくわかんねぇなって思ったらそちらをご覧ください。
2023/06/01 以前にこの記事を読まれた方へのお詫び
この記事を公開したとき「空集合はあらゆる集合の部分集合である」という主張は公理[1]である、と書いていたのですが空集合の公理、集合の包含関係の定義、論理学における含意の定義から導出可能な定理でした。申し訳ありませんでした。思い込み怖い。
「要素を持たない集合が存在する」という主張を空集合の公理と言います。数式で表すと以下です。
すなわち空集合に対してはどのような対象
の真偽を判定すればよいです[2]。
ここで
は常に
空集合があらゆる集合の部分集合になるというルールに矛盾する
細かいことは抜きにして簡単に説明する。「配列のすべての要素が条件を満たすなら True を返す」関数について考察したい。どんな「条件」かは明記されていないが、優れたプログラマであれば「どんな条件を与えても」成り立つように議論を進めてしまえばよいと気づくだろう。
「配列
数式に慣れていない人に向けて説明しておくと、右辺は「
ここで条件
という2つの集合に分割することができる。分割とは
となっていることをいう(
つまり本質的には条件判定
の形で定義できる[5]。
と書いてよいことにしよう[6]。
この事実を用いれば「配列のすべての要素が条件を満たすなら True を返す」関数
日本語に直せば「配列
集合
が成り立つことである。この真偽を判定する命題関数を
である。すなわち
さてここで
となる。ゆえに「配列のすべての要素が条件を満たすなら True を返す」関数
となる。Q.E.D.
「細かいこと抜きにして」の「細かいこと」
上記の議論はプログラミングにおける「配列」と数学における「集合」を同一視して議論を進めている。「細かいことを抜きにして」と言ったのはこの「同一視」の説明を省いているからである。
プログラミングの文脈で特にそれ以上の文脈を指定しないで単に「配列」と言えば大抵は
- 同じ型のデータが順序を持って複数並べられた構造
のことを指す[7]。
たとえば大抵のプログラミング言語で [1, 2, 3, 4, 5] とか ['a', 'b', 'c', 'd', 'e'] のように表記されるデータのことであって、数字の配列は数列、文字の配列は文字列と言ったりもする。空の配列とはひとつも要素のない配列、つまり [] のことを指す。
プログラミングにおける配列は順序を持ち要素の重複を許す[8]が、数学の集合は順序を持たず要素の重複を考慮しないので異なる構造である。
しかし配列の各要素に対して条件を適用して [True, False, True, False, True] のような状態になって、あとは論理積を取るだけという状態になれば、論理積には順序の交換法則が成り立つので順序は無視できる[9]。また、数学の集合は重複を許さないわけではなく考慮しないだけである(重複があろうがなかろうが議論の結果に影響しない)。ゆえに条件を適用したあとはもとの「配列」がどのような構造であったとしても集合と同一視できる構造になる。
重複について不安が残るなら以下のように考えてもよい。Boolean 型の配列、たとえば [True, False, True, False, True] のすべての要素で論理積を取ったときに結果 T/F のどちらになるかを知りたければ、その配列から重複を削除して得られる(数学的な)集合に対して T/F を定めても結果は変わらない。Boolean 型の配列から重複を削除して得られる集合は以下の4パターンしかない。
| 重複削除後の集合 | どんなときに得られるか | 重複削除前の例 |
|---|---|---|
| 空の配列 | [] |
|
| True しかない配列 | [True, True, True] |
|
| False しかない配列 | [False, False] |
|
| True と False が混在する配列 | [True, False, True] |
これらの集合に対してそれぞれ出力を決めればよい。
厳密に議論するにはこの辺にも言及しながら説明するべきなのだが、辻褄合わせのためだけに読みにくい記事を書いても意味がないので簡略的な説明にした。
状況によって変えるのは自然ではない
しかし条件
名前とは人間が勝手に付け加えた構造[11]なので、名前による場合分けは人間が手作業で行うしかなく、数が増えてくると人間が対応付けを間違って論理バグを仕込むのがオチである。
「空の配列が与えられたときに
超簡単な説明
記事を公開してから数式が理解できないという意見がけっこう見られたので超簡単に説明する。
まず条件
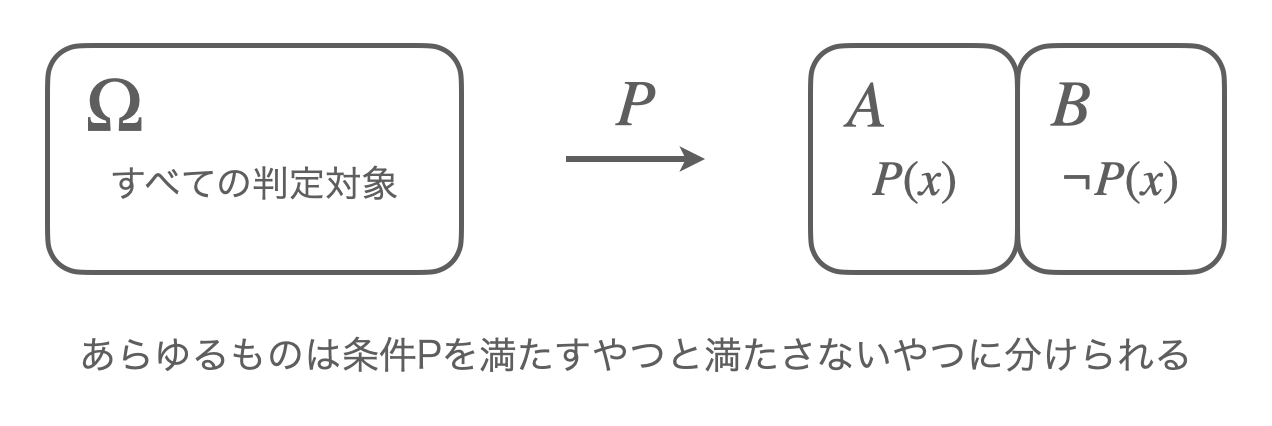
「すべての要素が条件
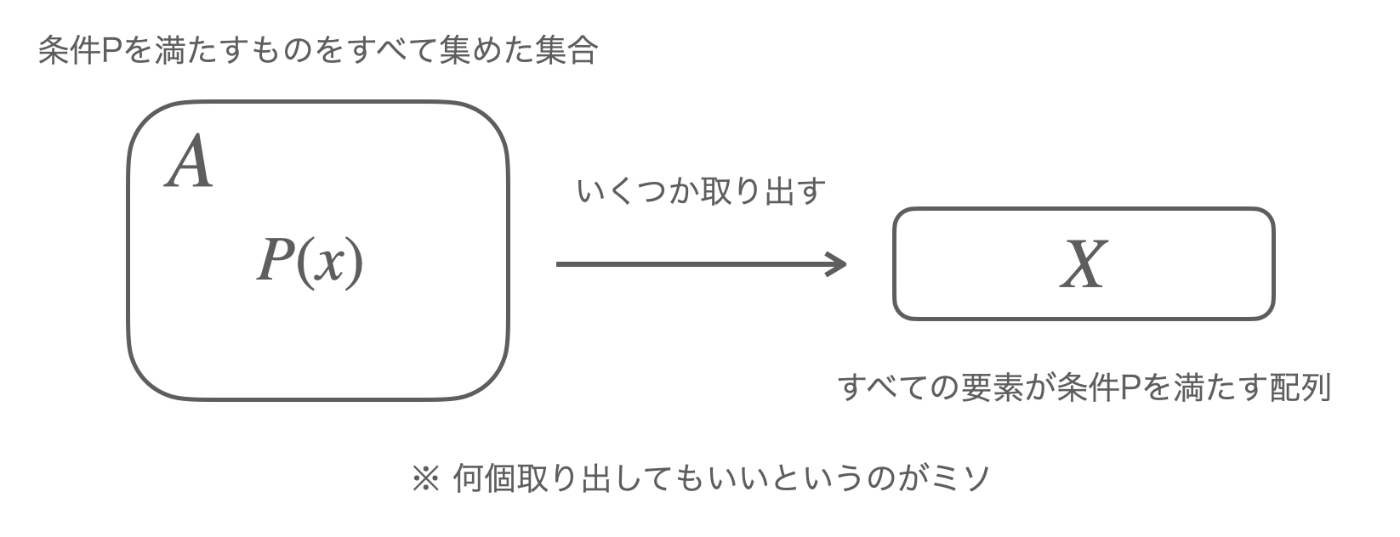
実際に「
空の配列とは空集合
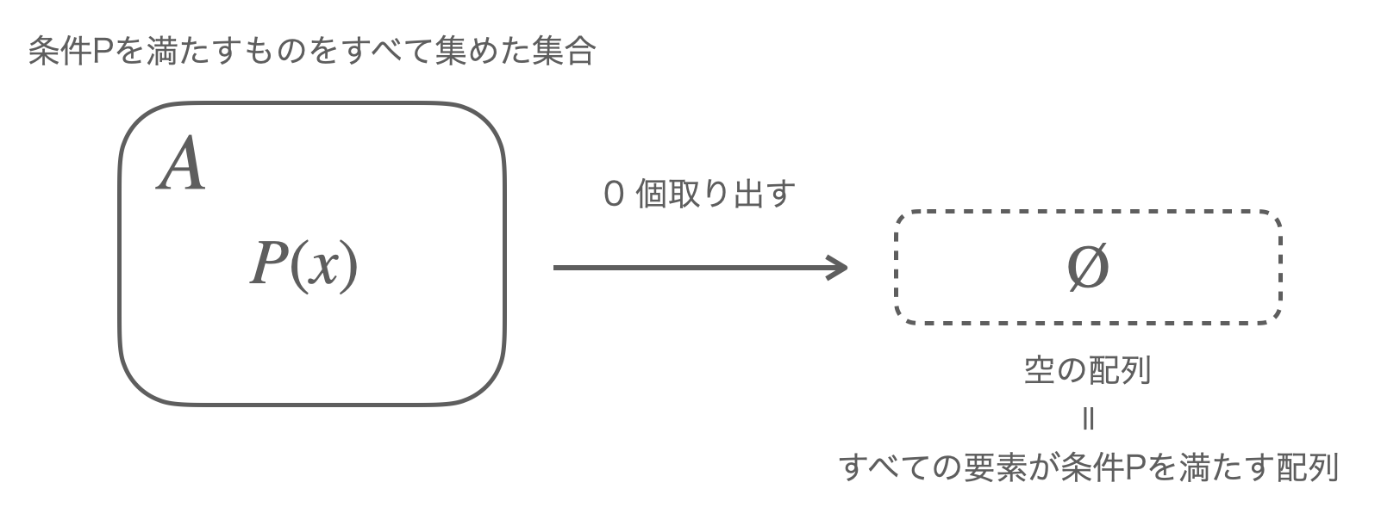
おしまい
-
数学的な理論を構築するとき一番はじめに定めるもっとも根本的なルールのこと。公理の真偽は(別の公理系を用いない限り、あるいは用いたとしても)証明できない場合がある。 ↩︎
-
以下の記事では
\forall x \in A. \, x \in B -
Vacuous truthという論理学の決まりがあって、この時点で
\forall x \in X. \, P(x) P X {\rm True} {\rm True} {\rm True} -
プログラマの脳を刺激するために付け加えておくと、
F P -
判定不能命題のときもこの形で定義できるの?という質問があったが多分できないので、本記事の証明の流れに沿うことはできない。判定不能命題のときは
P -
「配列」という概念自体がプログラミング言語によって微妙に異なるし「空の配列」もどのような実装になっているかは言語ごとに思想が異なる。この点を指摘して「文脈が曖昧である」と言っているならまぁ理解できなくはないが、それ以上議論が進まないので建設的な指摘ではない。 ↩︎
-
数学の言葉で言えば直積集合である。 ↩︎
-
多くのプログラミング言語においては論理積の短絡評価が行われるので
Falseを見つけた時点で他の値を評価せずに結果をFalseにする仕様になっている。その意味で「論理積をとる順序を変えたら動いたり動かなかったりするプログラム」は作れるし、ベテランのプログラマは意図的に作ることもあるが、今回の文脈では重要ではない。 ↩︎ -
ものすごいハックをすればできるのかもしれないが普通はできない。 ↩︎
-
同じ機能を持った条件
P P P
Discussion
「配列のすべての要素が条件を満たすなら True を返す」関数Aと「配列にひとつでも条件を満たさない要素があるなら True を返す」関数Bを考えます。空でない配列に対してはA、Bどちらかの関数の返り値がTrueになりもう片方はFalseになるが、空配列に対してはどちらもTrueが返ってくるということですかね。
いえ、関数Bのほうは False です。
関数Aのほうの定義は
で関数Bの定義は
であり、
となるので、
です。G(\varnothing, P) = {\rm True}
1つ気になったので質問させてください
関数に空の配列を渡したらアラートやエラーを吐き出すべきという主張に対しては上の集合の概念で反論可能でしょうか?
上の説明は「この世のものは「条件Pを満たすか満たさないか」に分けられる」という前提に基づいていると思われますが、TrueでもFalseでもない出力であるエラー出力はその範囲外であるように思われます。
とすると、「プログラミング上で空の配列を渡したらどうすべきか」という問いに対して果たして集合論で議論することは妥当か?という疑念が発生しそうなのでそこらへんの考えをお聞きしたいです。
いいえ。ここで説明した体系の中にはアラートやエラーという概念が登場しないので、この記事の中にあるような集合論の説明を用いてアラートやエラーの是非について言及することはできないです。
ただ「アラートやエラーを吐き出すべき」という主張が数学的な根拠に基づかない(基礎的な定理や公理に帰着できない)のであれば、それはただのお気持ち表明ですから、正しさという観点でどちらを信用するか考えたら比べるべくもないと思います。冒頭の「議論の余地がないレベル」とはそういう意味です。
個人的な感想としては、オッカムの剃刀ではないですが、論理学と集合論を用いて十分に説明できることにエラーという余計な概念を付け加えてしまったがためにどんな答えになるのかわからなくなってしまうのでは本末転倒だと思います。
証明するにしても、アラートやエラーを付け加えて拡張した論理体系を作って証明してくれればよいと思うのですが、それで「既存の論理学や集合論とは異なる結論になりました」と言って、誰がそんな論理体系を使うのかという話にもなります。そんな根本的な部分に変更を加えてしまうと、これまで過去の天才たちが積み上げてきた「数学」という膨大なライブラリのすべてを見直す必要が出てきてしまうからです。
そんなわけで、数学の体系を拡張したり再構築したりするときは、よっぽどの理由がない限り過去の重要な結果を壊さないように作られます。たとえば複素数は実数の拡張ですが、それによって実数が持っていた性質を壊したりしませんよね。したがってアラートやエラーを扱えるように拡張された論理体系においても、記事中のF(X, P) X {\rm True}
エラーは種類が多いので一般化した議論が難しいですし、エラーを含む理論を構築するならどうなるかという話なので決まった答えもないと思いますが、少なくとも lions28 さんがいま懸念されている範囲であれば、エラー出力を返しているのは記事中のF(X, P) P F
ゆえに「条件判定不可能なデータを含む配列X F(X, P) F
それでもエラーを raise したい、という場合もあると思うのですが、それは別にF F F F
実装がこうできてしまう以上、数学的にも理論構築の際に同様の回避策を取れてしまうと思います。というわけでご質問にある範囲なら「空の配列に対してF(X, P)
大変丁寧にご説明頂きありがとうございました。
仰って下さった説明には妥当性があると思いますし、納得することができました。
初心者です。数式が分からなかったので超簡単な説明、の部分をお読みしての質問です。
空集合は任意の集合の部分集合、であるので、集合Bの部分集合でもあると思います。集合BはP(x)がFalseとなるxの集合であるため、空集合はFalseとなるべき、という主張も可能かと思います。
こちらについて、コメント/ご説明いただけると幸いです。
一言で言えば、論理的な同値性を崩さないように「X \subset B X P
これはX \subset B X P X
「X \subset B X P
はどちらも空の配列を与えたときに True を返します。後者がX \subset B
だと思えば True になりますね。
丁寧なご回答ありがとうございます。回らない頭で必死に考えて下記まで理解できました。
①空集合は任意の集合の部分集合、であるので、集合Bの部分集合である
②したがって空集合からなる配列Xの要素はすべて条件Pを満たさない
③配列Xの要素がすべて条件Pを満たさないとき、関数Fの出力はFalse
④空集合に対してはFalseが返る
という風に考えてしまったのですが、どこが間違いっているかご教示いただけないでしょうか…?初心者で申し訳ありません
「配列X P X P
「配列X P X P
私は
true派ですが、いくつか質問したことがあります。これは本当に正しいですか? 脚注でWikipediaの記事にリンクされていますが、当該記事の命題論理における説明からは上記の述語論理に関する主張は自明ではないと思いました。P(x) P(x) P(x)
p(x)が対応しています。決定可能なlions28さんへの回答の中で、
と述べられていますが、そのような理論体系こそ読者が関心を持っている体系なのではないでしょうか? また、そのような論理体系で問題なく「
trueが返った方が嬉しい」という結論に至れるかと思いますので、そのような体系上で論じた方が読者にとって有用だと思いますがいかがでしょうか?正しくないです。『超簡単な説明』は雑に書いてます。『超雑な説明』と題打ったほうが実態として正しいです。
そのため『空集合があらゆる集合の部分集合になるというルールに矛盾する』では条件P \Omega P
本記事の中でやっている、条件P A
は実は同じことなんだよ!と説明する流れは、それを知らなかった人に驚きを与えるためのエンターテインメントであって、数学的には最初から条件P P
論理学の中で決定不能な条件をどう扱うかまで気になる人はこんな記事にとどまってないで数学書を読んでくれ、と思いますので私もそこまでリサーチするつもりはなくここからは推測ですが、この議論をもっと根源的な命題にまで還元すると結局は
という命題はP(x) {\rm True} P(x) P
このときの「P(x)
そうですね。lions28 さんへの回答は Haskell の Maybe Bool のリストの挙動を意識して書いてる(例外には Nothing が対応)のでそれくらいの複雑さで済むなら別に記事に書いてもいいかなとは思うのですが、手元の資料では一般論としてそれで「すべてのエラーを考慮した論理体系になったのか」の裏付けが取れなかったので書いてないです。「条件P
闇ぶいれこさんは何か知ってそうな雰囲気出してるので記事書いてくれたら読みに行きます!
元々のゴールは
all([], p)がtrueを返すと何が嬉しいのかを考える物だと私は理解しています。つまり vacuous truth があると何が嬉しいのかを考えるとも言い換えられます。そのルールは vacuous truth そのものなので、そこに立脚してしまうと
true派以外の人は到底納得できない説明になってしまう気がします。(true派の私も納得できていないです)そう思うならあなたが記事かけば?ってやんわり言ったつもりですが伝わらなかったでしょうか。
別に判定不能命題じゃなければこの記事の説明でいいですし、判定不能命題ならこの記事に沿った説明は諦めて他になんか適当に同値な命題探してくればいいんじゃないでしょうか。
どうせ公理まで還元していくと vacuous truth に行きついちゃうので vacuous truth が納得できないならいっそそっちが成り立つ理由の説明でも探したほうがいいんじゃないですね。
「A B A B
とする。両辺で否定を取れば、二重否定律とド・モルガン律より
となり、この真理値表を書いてみると{\rm False} \Rightarrow B B {\rm True}
ちょっと個別に質問に回答するの疲れたのでもう回答しないです。記事の修正が必要なご指摘等は引き続き投げてもらってかまいません。
すべてFalseになる集合にも空集合Φって含まれるはず、という理解をしています。※集合の分割を行った場合の分割後の集合同士の共通部分として空集合がありますhttps://ja.m.wikipedia.org/wiki/%E9%9B%86%E5%90%88%E3%81%AE%E5%88%86%E5%89%B2
今回の証明の流れに沿うとFalseの場合にも同じことが言えてしまうと思います。
『超簡単な説明』のほうではそう感じるかもしれません(簡単にしただけ穴は増えるので)が『空集合があらゆる集合の部分集合になるというルールに矛盾する』のほうの流れでもそうなるか確認してもらえますか?思うだけでなく具体的に示してくれたら修正します。
lions28 さんへの回答を参考にしてもらえますか?
返信ありがとうございます。
本質的には、本文中の『対象xが条件Pを満たすかどうかは集合Aに属しているかどうかで判定できる』という文言に引っかかっています。
空集合はAの部分集合でもあり、Acの部分集合でもあります。
引用部分とその対偶を考えると、空集合は条件Pを満たすかつ条件Pを満たさない、という事になるはずですが、これはなにかおかしいです。
なにか前提としているものが自明でないのかなっと思っていますが、ごめんなさい、どこをどう修正すればよいかは検討ついていません。
「対象x P A x
はい。そのとおりですね、空集合がPを満たすなんて書いてしまいました。言いたいのは、例えば、配列の要素数が1以下のときだけを考えたときにFalseとTrueは対称になる(入れ替えても議論が成立する)ので今回の結論が不思議だなっと思ったことです。具体的に説明する時間あれば追記するので放置ください〜。
False と True を入れ替えても同じ命題の真偽を示していることにしかならないです。
時間空きました。
記事の内容は雑かもしれませんが下記のとおりだと思っています。記法は素朴かもしれませんが伝わると信じています。。
すべての元xがなす集合をUとする。与えられた条件Pに対して、Pを満たす元x∈Uの集合をG⊂Uとする。与えられた配列Xは集合Uの部分集合となみす(X⊂U)。「配列Xのすべての要素が条件Pを満たすなら True を返す」関数Fを下記のように定義する
F(X) = True : X ⊂ Gの場合
= False : それ以外の場合
このとき、配列が空の場合、集合とみなしたときのXは空集合Φ。Φの性質としてΦ⊂Gが成り立つのでFはTrueを返す。
個人的に記事は分かりやすくなぁと納得していますが、下記のようにも考えられます。
「配列Xのすべての要素が条件Pを満たすなら True を返す」を「配列Xに条件Pを満たしていない要素が一つもないなら True を返す」と解釈します。そして関数をHとして、下記のように定義します
H(X) = True : X∩Gが空集合でないかつX∩Gcが空集合の場合
= False : X∩Gが空集合であるかX∩G^cが空集合でない場合
ここでG^cはGの補集合です(見にくくてごめんなさい)。ドモルガンの法則的には排中律を満たしています。
ここでXが空集合Φのとき、空集合の性質から X∩GはΦですから、関数HはFalseを返します。
自然言語の解釈を数学的にどう表現するか?するか?の問題だと思っています。
間違ってたら恥ずかしいですが、ご指摘いただければ幸いです:D お付き合いいただきありがとうございます。
???
だったらまず\exists x \in X. \, \lnot P(x) X \lnot P(x) X {\rm False} {\rm True}
∀x∈X.P(x)
もうこう書いてしまえば議論の余地はないですよね。Xが空集合の場合はTrueになるのは承知しています。主張したいのは、自然言語から数式に落とすときに不定性があるのでは?という点です。
あなたの主張は...循環論法
定義の中に入っていますから、空集合に関してFalseが返るのは自明ですよね。主張は空集合に関してFalseが返る、空集合でないXに関しては境内の条件を満たす関数が定義できる、というものでした。
ちなみに。X ⊂ Gの場合にTrueを返す関数を考えてXが空集合の場合にTrueになるのも自明では?と思いましたがどう違うのか教えてくだされば嬉しいです。
もう指摘じゃなくて質問になってますよね……納得するまで丁寧に教えたらバッジの1つでも送ってくれるんでしょうか。試してみますね。
記事の最初で親切にも「議論の余地がないレベル」って書いたと思います。教科書通りの翻訳です。そう書かない数学書があったらむしろ興味あるので教えてください。エビデンスカモン。
うーん、私は最初に
と言ったんですけど確認しましたか? まぁ記事が読みづらかったかもしれないので要約します。
『空集合があらゆる集合の部分集合になるというルールに矛盾する』のほうの論理の流れは
です。形式的な推論(文字列の置換だけで機械的にできる推論)でできることを、記事の中ではみんながわかりやすいように自然言語を混えて書いてるだけです。前提は
の3つであって「X \subset P F(X, P)
そう言われても「あなたの翻訳ミスでは?」としか……
定義として数式に落とすときの自由はもちろんありますよ。でも推論は自然言語でやると間違いが起こるからルール決めて数式でやろうぜ、ってのが現代の数学なわけで、H(X)
という複雑な推論を自然言語でやるのは危険です。まぁ今回は原因はそこじゃなくてマジでただの翻訳ミスなんですけど。あなたは「配列Xに条件Pを満たしていない要素が一つもないなら True を返す」を
で定義してますが、「配列Xに条件Pを満たしていない要素が一つもないなら True を返す」を素直に翻訳するならH(X)
ですよね。この定義でも十分に機能を果たします。それで、X \cap G \neq \varnothing {\rm False}
あなたが言うような関数H(X)
さすがに疲れたんですけどもういいですか? 見返りに何か私の知らない知識を教えてくれるとかなら歓迎するんですけど……
繰り返しになりますが個別の質問に回答するの疲れたのでもう回答しないです。回答する場合にも塩対応、煽り、暴言等が含まれうる旨、ご了承ください。
記事の修正が必要なご指摘等は引き続き投げてもらってかまいません。