🎣

【量子コンピュータ】IBM量子開発者認定試験(C1000-112)サンプル問題をしがんでしがんで舐め回す(前編 Q01-10)

2023/09/04に公開

Python

量子コンピュータ

Qiskit

tech

みなさんこんにちは！
この記事は，IBMが提供する量子開発者認定資格試験 Exam C1000-112: Fundamentals of Quantum Computation Using Qiskit v0.2X Developerサンプル問題の解答と解説記事です！
IBMは, 当IBM量子開発者認定という資格を提供しており，その資格取得のためには当試験のpassが必要がです。(筆者は2023年8月にIBM量子開発者認定を取得。取得ホヤホヤ🍲で本記事執筆中です！)

本記事はとにかくボリュームが多いため、試験自体の説明は概要に留め, サンプル問題の解説に集中しています。
また，本前編/後編に分け，前編はQ01.~10, 後編はQ11.~20を扱います。
後編は下記記事にまとめておりますので，この記事読んだ後に是非お越しください！

もし本試験の詳細や私自身が受けようと思った動機や目指すこと, 私自身の合格体験記などにも興味を持ってくださる方がいれば，どうぞ別記事に来てくださればと思います！
それでは，早速本試験の概要と解説の構成を説明します。

IBM量子開発者認定資格(C1000-112)とは？

詳細は別記事に記載しますので，Linkだけ貼っておきます。

main page

認定資格提供開始のプレスリリース(2021年4月)

C1000-112試験は過去問題は公開されていませんが, サンプル問題という形で20問の例題が公開されています。上記のmain web pageの右列にpdfへのリンクがあります。
本記事はそのサンプル問題の解答例，および関連知識をまとめた記事です！

↓サンプル問題へのリンク場所(下記画像の垢枠内)

本記事の概要

上記の通り, 本試験には過去問題集がないため,　サンプルにある20問題から本試験で問われる基礎と実用の知識考え方を抽出しなければなりません。ですので, 1問1問じっくり解説していきます！例えば，本資格試験は選択式のため，正解の選択肢がわかるだけでなく，不正解の選択肢が「なぜ不正解か？」までをちゃんと理解するのがベストです！タイトルのしがんでしがんで舐め回すはこの考え方を由来としています🤗 本記事はその要件を満たすように解説を進めていきます！
上記の理由から本記事は，答えに至るまでの道筋をできる限り丁寧に解説しているため，基礎を理解している方からすると冗長な内容になっています💦　例えば，設問によっては計算部分を行列形式とディラック形式に書き分けて解説していたりします。また，すでに解説済みの計算が出てきても極力省略せずに解説するように心がけています。ですので，冗長な一方で量子計算関連の知識や考え方が十分に定着していない初学者の方には親切な内容になっています😋
大まかに理解する上で計算自体はそんなに重要ではありませんが，今後量子計算を実装していく予定がある方には，数式の取り扱いにも慣れておく必要があるため丁寧に記載しています。ただし，読んでいても分からなくなってしまう場合は，深追いするよりすっ飛ばして後で戻ってくるくらいの心づもりが良いと思います😊

解説の構成

単純な解説だけでなく，その問題の背景や専門用語，数式処理，シミュレーション結果など内容が盛りだくさんです！なので，それぞれにSectionを設けて解説しています。項目は下記の通りです！
(下記の#には問題番号が入ります。)

問題Part

Q#. 問題

問題文
選択肢一覧

A#. 解答

正解選択肢

解説Part

Q#.1 用語

そもそも用語が分からなくて手が出ないときがありますね。チャジれば(chatGPTに聞けば)いいですが，サクッと進むために私が簡潔に用語解説します！

Q#.2 背景

筆者の理解の範囲で問題の背景や関連事項を紹介します！

Q#.3 選択肢解説

選択肢の解説です。概要で述べた通り，正解だけでなく不正解選択肢も舐め回します👅　皆さんは「なんで不正解なの？」と思うときないでしょうか？私はめちゃくちゃあります。「なぜ不正解となるか？」を的確に答えることも，正解を答えられることと同じくらい大事だと思っています。故に，冗長になることを承知で不正解の理由も詳しく述べます。設問によっては，「こう直せば，正解になる！」まで言及し，proactiveな解説にしていきます！

Q#.4　qiskitシミュレーション

手計算だけでなく，qiskitを用いたシミュレーション結果も紹介します。ただし，Code部分はgithub上に残したjupyternotebookの方を参照してください！

Q#.5 Qiskit API

設問に関係するqiskit API referenceのリンクを記載します！気になるものをチェックしてみてください！

それでは早速始めていきましょう！
第1問は基本的な量子回路における量子，古典ビットの指定方法の知識に関する問題です！

Q1.

Which statement will create a quantum circuit with four quantum bits and four classical bits?

[A]
QuantumCircuit(4, 4)

[B]
QuantumCircuit(4)

[C]
QuantumCircuit(QuantumRegister(4, 'qr0'), QuantumRegister(4, 'cr1'))

[D]
QuantumCircuit([4, 4])

答え

[A]

Q1-1.用語

選択肢[C]にRegisterという単語が出てきましたね。古典コンピュータでのレジスタとはなんだったでしょうか？レジスタは，データや処理を格納する場所である点でメモリと似ていますが，CPU内に存在している点が異なります。容量は限られている代わりにCPUと連携して動作できる分，高速な処理が可能です。メモリは記憶領域にあるので，大容量のデータを保存できる一方で動作は遅くなります。
これから扱う量子ビット, 古典ビットは全て回路内に存在していることを想定しているためメモリではなくレジスタという表現が正しいことですね😋

Q1-2.背景

まず，量子ビットと古典ビットの両方を用意しないといけない理由はなんでしょうか？量子コンピュータでは，重ね合わせやエンタングル状態といった量子ビット特有の状態を使って計算を実行しますが，量子ビットの状態を制御したり，状態を測定したりするのは古典ピットの役割なのです！ですので，古典ビットは量子計算の制御や制御フローの管理において重要な役割を果たしていると言えるのです😋
問題文は４つの量子ビットと4つの古典ビットを作るCode分の作成を求めています！

Q1-3.選択肢解説

qiskit APIには，QuantumeCircuit Classが準備されており

qc = QuantumCicuit(q,c)

と書くことで,量子ビットをq個，古典ビットをc個をレジスタに格納した量子回路のインスタンスを作ることができます！また，ここでは取り上げていませんが下記のように量子，古典レジスタを使って回路を構成しても，問題文と同様の回路が設計できます！

QuantumCircuit(QuantumRegister(4,"q"), ClassicalRegister(4, "c"))

[A]
上の解説のq, cにそれぞれ4が入ったcodeとなり，4つの量子-古典ビットを有する量子回路を作ります。これは題意を満たし正解となります！

[B]
引き数を1つにする場合，その数の量子ビットが作られるため 4つの量子ビットを持つ回路となります！古典ビットを準備できていないので不正解です！

[C]
名称指定されているqr0量子ビットレジスタが4, cr1量子ビットが4つの合計8つの量子ビットが準備された回路となります。こちらも古典ビットが準備できておらず，量子ビットの数も合わないため，残念ながら不正解です！

QuantumCircuit(QuantumRegister(4,"q"), ClassicalRegister(4, "c"))

とかけば正解でした！

[D]
選択肢のようにリストは引数として受け入れません！よってエラーとなってしまいます！
それぞれの数はリストの外に出して，第1引数: 量子ビット数，第2引数: 古典ビット数となるようにしましょう！

Q1-4. シミュレーション

この問題はシミュレートすることないのでSkipします！

Q1-5. Qiskit API

QutumCircuit

さて，第2問です！
今度はある初期状態に回転操作を加えた後の操作後の状態の測定確率に関する問題です！

Q2.

Given this code fragment, what is the probability that a measurement would result in $\ket{0}$ ?

qc = QuantumCircuit(1)
qc.ry(3 * math.pi/4, 0)

[A]
0.8536

[B]
0.5

[C]
0.1464

[D]
1.0

答え

[C]

Q2-1.用語

ry(3*math.pi/4,0)はQuantumCircuitクラスに用意されたY軸方向の回転操作メソッドです。ブロッホ球上の状態ベクトルに対して，Y軸方向に $\frac{3 \pi}{4}$ 回転させるユニタリ操作を表します。ちなみに，"Y軸方向に回転"とは，ネジを締める側に回したときに進む方向をY軸正方向としたときに，その回転方向を正方向とします。
また，しれっとmeasurementが出てきています。量子力学における測定は古典力学での測定ほど単純ではなく測定に確率的な要素が含まれます。この辺りは，計算をしながら考え方を確認していきましょう！量子力学的測定に関する詳しい背景は Q4.で扱うのでそこまで待ってください！

Q2-2.背景

測定確率の計算は，ディラック記法を用いて計算してみましょう！また，状態ベクトルの回転についてはおなじみのブロッホ球を使って考えてみましょう！回転操作については直感的に理解できるので重宝しますね！これをぐりぐり回せるシミュレーションをUnityとかで描けるようになりたいなぁ🌛と思って，この記事執筆と並行して試しに作っていますが，難しい。。。。

Q2-3. 選択肢解説

初期状態 $\ket{\Psi_{0}} = \left( \begin{matrix} 1 \\ 0 \\ \end{matrix} \right)$ に対して, Y軸方向に $\theta = \frac{3 \pi}{4}$ 回転させた場合に, $\ket{0}$ が観測される確率を求める問題です。

一般に, 初期状態 $\ket{0}$ のみを持つ状態 $\ket{\Psi_{0}}$ に対して，Y軸方向の $\theta$ 回転後の状態 $\ket{\Psi'}$ はA
$\ket{\Psi'} = \cos{\frac{\theta}{2}} \ket{0} + \sin{\frac{\theta}{2}\ket{1}}$ となります。
上式が得られる理由は，Y軸方向の回転を操作する行列が

\begin{align} R_{Y}(\theta) &= \left( \begin{matrix} \cos{\frac{\theta}{2}} & - \sin{\frac{\theta}{2}} \\ \sin{\frac{\theta}{2}} & \cos{\frac{\theta}{2}} \end{matrix} \right) \end{align}

で表されるためであり, この行列を $\ket{\Psi_{0}}=\ket{0}$ に作用させると， $\ket{\Psi'}$ が得られることが下記の計算で確かめることができます！自分でもやってみましょう！
$\ket{\Psi'}$ が得られる過程は下記の通りです。

\begin{align} \ket{\Psi'} &= R_{Y}(\theta) \ket{\Psi} \\ &= \left( \begin{matrix} \cos{\frac{\theta}{2}} & - \sin{\frac{\theta}{2}} \\ \sin{\frac{\theta}{2}} & \cos{\frac{\theta}{2}} \end{matrix} \right) \left( \begin{matrix} 1 \\ 0 \end{matrix} \right) \\ &= \left( \begin{matrix} \cos{\frac{\theta}{2}} \\ \sin{\frac{\theta}{2}} \end{matrix} \right) \\ &= \cos{\frac{\theta}{2}} \ket{0} + \sin{\frac{\theta}{2}} \ket{1} \end{align}

となり， $\ket{\Psi'}$ が得られることが示されました。
では，ここから $\ket{\Psi '}$ に $\bra{0}$ を作用させて， $\ket{0}$ が測定される確率を求めてみましょう！

\begin{align} P_{\ket{0}} &= \braket{0|\Psi'}^2 \\ &=\Bigl( \bra{0} (\cos{\frac{3 \pi}{8} \ket{0}} + \sin{\frac{3 \pi}{8}} \ket{1}) \Bigr)^2\\ &= \cos^2{\frac{3 \pi}{8}} \braket{0|0} + \sin^2{\frac{3 \pi}{8}} \braket{1|0} \\ &= \cos^2{\frac{3 \pi}{8}} \end{align}

このとき，倍角の公式を使って $\cos^2{\frac{3 \pi}{8}}$ を計算してもいいのですが，ここではざっくりとした値を求める方法をとります！個人的には一意な値を求めるより，必要なスケール感で取り得る値の範囲を把握することの方が大事だと感じているからです！そのために角度 $\theta$ で $\cos^2{\frac{3 \pi}{8}}$ を評価すればよいわけです！

$\frac{\pi}{3}<\theta = \frac{3\pi}{8} < \frac{\pi}{2}$ と評価できるため，

\begin{align} \cos{\frac{\pi}{2}} & < \cos{\theta} < \cos{\frac{\pi}{3}} \\ 0 & < \cos{\theta} < \frac{1}{2} \\ よって， 0 & < \cos^2{\theta} < \frac{1}{4} \end{align}

つまり，選択肢の中で0より大きく $\frac{1}{4}$ より小さい値となり，答えは[C]となります！今回の問題は[C]以外の選択肢は上記の範囲に入らないため不正解です🙃

Q2-4.シミュレーション

観測される状態のヒストグラムを作る場合は，Aer Simulator が使えます。
当モジュールでは量子状態測定をノイズフリーシミュレーションできます。
量子コンピュータにおけるノイズとは，環境ノイズやゲートエラー，量子ビット間の結合エラー，読み取りエラーなどが含まれます。それらのノイズがない，理想的な量子コンピュータを想定してシミュレーションされます。

回転後に測定される状態のヒストグラムは下記のようになります。

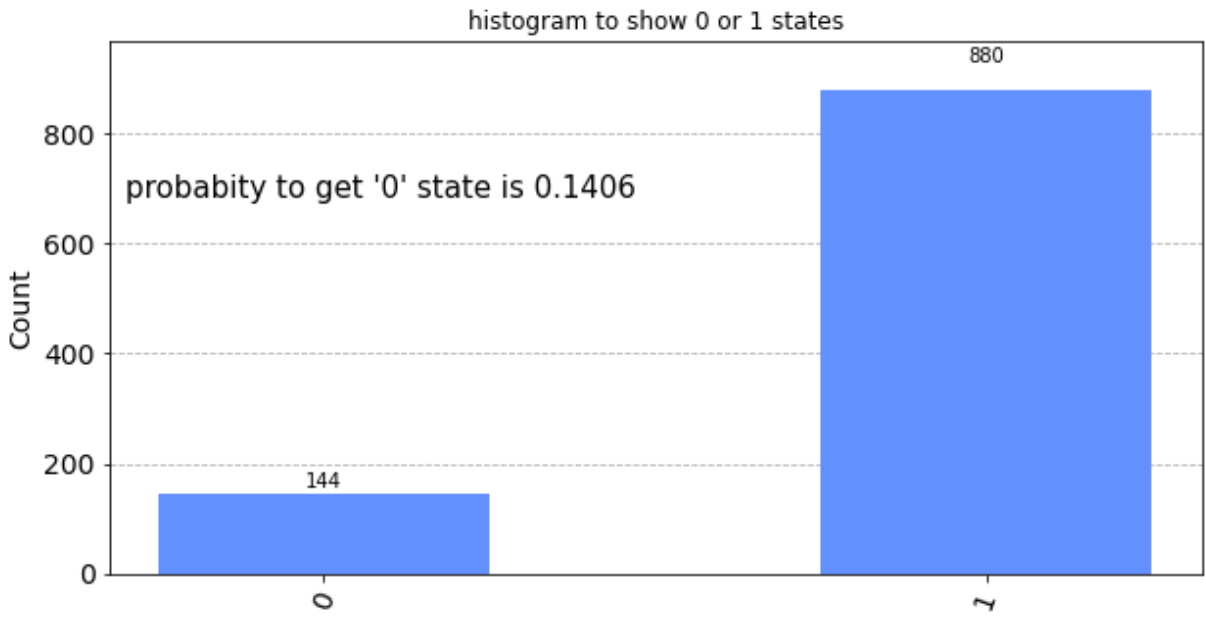
今回のシミュレーションでは，1024回の試行に対して, $\ket{0}$ が144回, $\ket{1}$ が880回測定されることがわかりました。つまり, 回転操作後に状態 $\ket{0}$ を得る確率Pは $P=\frac{144}{1024}=0.1406$ であることがわかり，選択肢[C]が最も近い答えであることがわかります！

また, bloch simulator を使ったBloch球上ベクトルもシミュレートもできちゃいます！
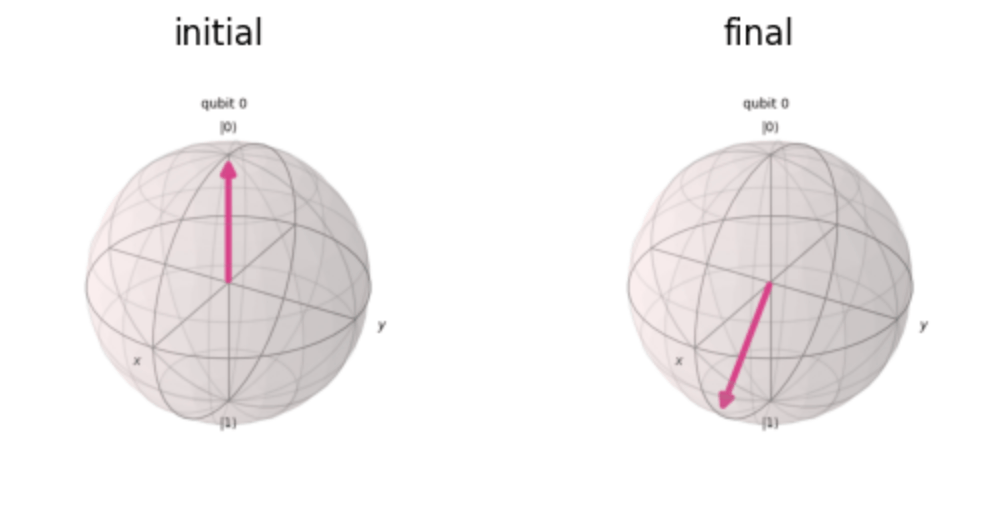
bloch　simulatorを使って， $\ket{0}$ をY軸方向に $\frac{3 \pi}{4}$ 回転した終状態を描画すると，下記のようになります！

確かに，Z軸の+方向から $\frac{3 \pi}{4}$ 回転しているように見えます！直感的に理解できていいですね！

さて次のQ3は, 与えられた図に応じた量子回路をqiskitで実装する問題です！

Q3.

Assuming the fragment below, which three code fragments would produce the circuit illustrated?

  inp_reg = QuantumRegister(2, name='inp')
  ancilla = QuantumRegister(1, name='anc')
  qc = QuantumCircuit(inp_reg, ancilla)
  #Insert code here

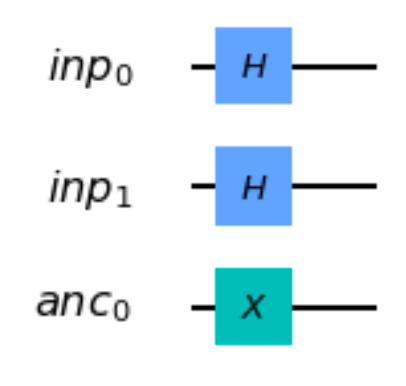
[A]
qc.h(inp_reg)
qc.x(ancilla)
qc.draw()

[B]
qc.h(inp_reg[0:2])
qc.x(ancilla[0])
qc.draw()

[C]
qc.h(inp_reg[0:1])
qc.x(ancilla[0])
qc.draw()

[D]

qc.h(inp_reg[0])
qc.h(inp_reg[1])
qc.x(ancilla[0])
qc.draw()

[E]
qc.h(inp_reg[1])
qc.h(inp_reg[2])
qc.x(ancilla[1])
qc.draw()

[F]
qc.h(inp_reg)
qc.h(inp_reg)
qc.x(ancilla)
qc.draw()

答え

[A], [B], [D]

Q3-1.用語

変数名にancillaという見慣れない言葉があります。これは量子回路で登場するancilla bitのことを指しています。アンシラビットとは，エラー訂正のパリティチェックやアルゴリズム実行時に一時的に情報を保持するために使われます。計算の結果には直接影響を与えないことが多く，あくまで補助的な役割を果たしていることがアンシラとして定義する要件です！勉強を始めた当初は　Target bitの状態を制御することもありアンシラビットに含まれるかと思っていましたが，計算結果に影響を与える点でアンシラには含まないようです。
制御ビットは，特定の条件下で量子操作を制御するために使用され，制御ゲートの制御線として利用されていると言えます。

Q3-2.背景

inp_regの0から1番目にq0, q1量子ビットが格納されており，ancillaの0番目にanc量子ビットが格納されています。
アダマールゲートとNOTゲートについて解説しましょう！

アダマールゲート

アダマールゲートが使われる最も簡単な例は，量子ビットの重ね合わせです。
アダマール変換は

\begin{align} \hat{H} &= \frac{1}{\sqrt{2}} \left( \begin{matrix} +1 & +1 \\ +1 & -1 \end{matrix} \right)\\ &= \frac{1}{\sqrt{2}} (\ket{0}+\ket{1})\bra{0} + \frac{1}{\sqrt{2}}(\ket{0}-\ket{1})\bra{1} \end{align}

と表されるため，始状態が $\ket{0}$ のとき，終状態は $\frac{1}{\sqrt{2}}(\ket{0}+\ket{1})$ , 始状態が $\ket{1}$ のとき，終状態は $\frac{1}{\sqrt{2}}(\ket{0}-\ket{1})$ となります。
このように，アダマール変換を用いると，初期状態が１つの状態のみを持つ単一量子ビットに作用した際に，量子ビットの重ね合わせ状態を作ることができます。量子計算をする上で大変重要なゲート操作です！

NOTゲート

NOTゲートは行列で書く場合，

\begin{align} \hat{X} &= \left( \begin{matrix} 0 & 1 \\ 1 & 0 \end{matrix} \right) \\ &= \ket{0}\bra{1} + \ket{1} \bra{0} \end{align}

と表されます！
これは，始状態が $\ket{0}$ のとき終状態は $\ket{1}$ , 始状態が $\ket{1}$ のとき終状態 $\ket{0}$ となります！
つまり，始状態と反対の状態に変換する変換がNOTゲートです！

与えられた画像からinp0 とinp1にアダマールゲート，anc0にNOTゲートを作用させる量子回路が与えられており，それらを実装するためのCodeを解答する必要があります！
今回この問題を解いていて初めて知りましたが，リストのスライス表現で複数の量子ビットに同じ量子操作を実施できるらしいってことを知りました。こういう知識の得方もありますね。やってよかった！

Q3-3.選択肢解説

[A]
QuantumCircuit.h(qubit)はパラメータとして，QuantumRegisterを取ります！
この時，複数のqubitを指定する場合，指定したqubit全てのアダマール変換を施します！

qc.h(inp_reg)  ##複数準備された量子ビットinp_regすべてにアダマール変換を施す
qc.x(ancilla)  ## ancillaにNOT ゲートを施す
qc.draw()

これは題意の通りのため，正解です😋

[B]

qc.h(inp_reg[0:2]) ##inp_regの0~1番目の量子ビットにアダマール変換を施す  
qc.x(ancilla[0])   ## ancillaにNOT ゲートを施す

これも題意の通りのため，正解です😋
[C]

qc.h(inp_reg[0:1])  ##inp_regの0番目の量子ビットにアダマール変換を施す
qc.x(ancilla[0])   ## ancillaにNOT ゲートを施す

これは，inp_regの1番目の量子ビットにアダマール変換が施されないため，題意を満たさず不正解です🙃

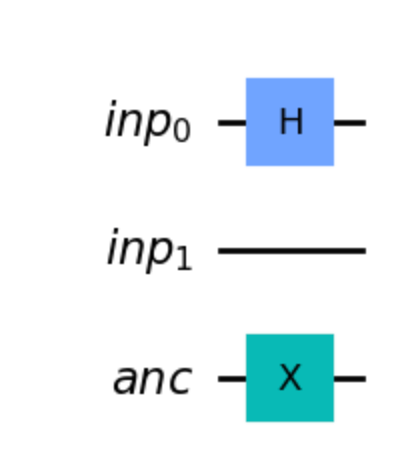
[D]

qc.h(inp_reg[0])  ##inp_regの0番目の量子ビットにアダマール変換を施す
qc.h(inp_reg[1])  ##inp_regの1番目の量子ビットにアダマール変換を施す
qc.x(ancilla[0])  ##ancillaの0番目の量子ビットにアダマール変換を施す

これは題意の通りのため，正解になります😋

[E]

qc.h(inp_reg[1])  ##inp_regの1番目の量子ビットにアダマール変換を施す
qc.h(inp_reg[2])  ##inp_regの2番目の量子ビットにアダマール変換を施す
qc.x(ancilla[1])  ##ancillaの1番目の量子ビットにアダマール変換を施す
qc.draw()

inp_regは, 0と1番目の量子ビットの2つしかなく，２番目の量子ビットは存在しません！
そのため，2行目で "IndexError: list index out of range"となりエラーとなります！そのため不正解です🙃

[F]

qc.h(inp_reg)  ##inp_regの0~1番目の量子ビットにアダマール変換を施す  
qc.h(inp_reg)  ##inp_regの0~1番目の量子ビットにアダマール変換を施す  
qc.x(ancilla)   ##ancillaの1番目の量子ビットにアダマール変換を施す
qc.draw()

0~1番目の量子ビットに2回の
アダマール変換が解かされており，題意に反すため不正解です🙃

Q3-4. シミュレーション

題意の回路に測定用の古典ビットを用意して，測定される状態のヒストグラムを計算してみましょう！

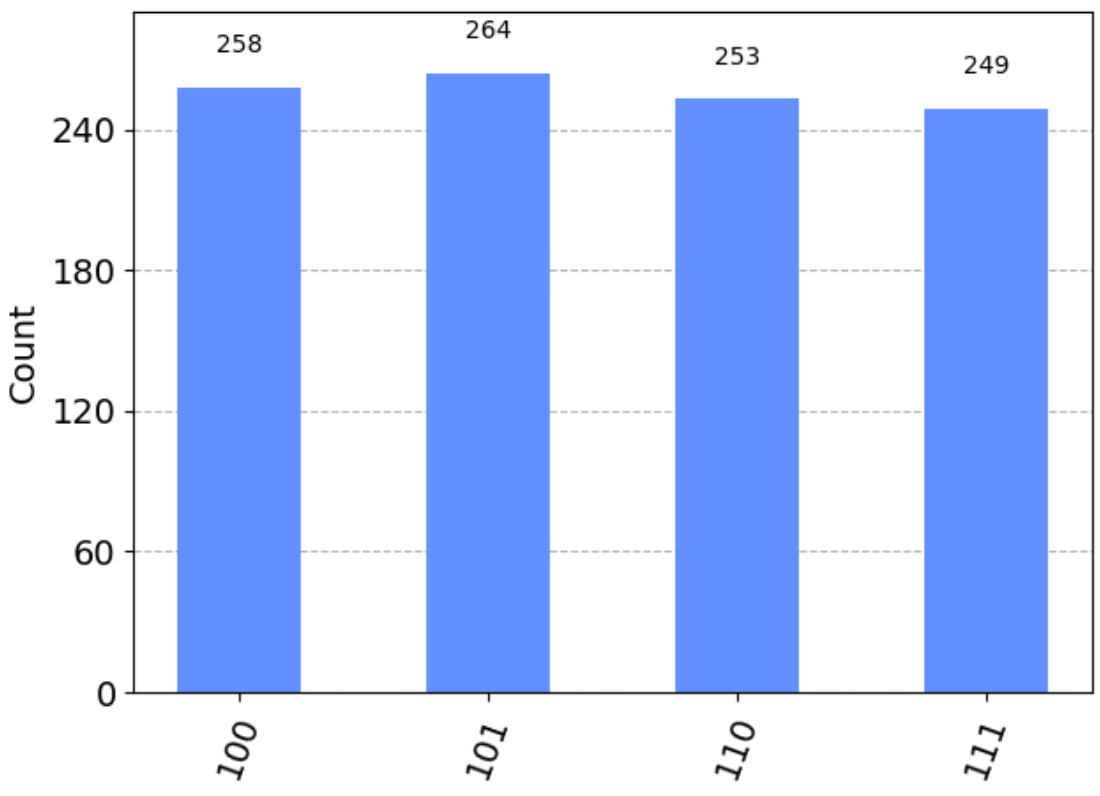
上記のヒストグラムから，どうやらこの回路で作られる量子状態は，
$\ket{100}, \ket{101}, \ket{110}, \ket{111}$ がおおよそ当確率で検出されるようです。

これらの結果は理論的に確かめることもできます!
ただし，直積状態の考え方を使うため，Q5の解説で　エンタングルしている状態，していない状態(直積状態)を学んでから戻ってくるのが良いかもしれません😭
サッと読んで理解が難しいと感じた場合は，次の問題に飛んじゃいましょう🛩
$\ket{zyx}$ と表現する場合，x, y, zはそれぞれ $x:inp_{0}$ の状態， $y:inp_{1}$ の状態， $z:anc$ の状態を指し，直積で表されています。
つまり， $\ket{zyx} = \ket{z} \otimes \ket{y} \otimes \ket{x}$ と計算されます。
本来であれば，それぞれの3つの量子ビットが0と1の２つの状態を持つため，
$\ket{000}$ ~ $\ket{111}$ の合計8状態を持ちうりますが，題位で示されている回路のようににおけるアダマールゲートとNOTゲートにより，取りうる状態の割合が変化した結果，
$\ket{100}, \ket{101}, \ket{110}, \ket{111}$ がおおよそ当確率で測定される状態に遷移するのです！
これを理論的に計算してみると，下記のようになります。

\begin{align} \ket{\Psi '} &= \left( \hat{X_{z}} \otimes \ket{0_{z}} \right) \left( \hat{H_{y}} \otimes \ket{0_{y}} \right) \left( \hat{H_{x}} \otimes \ket{0_{x}} \right) \\ &= \left( \ket{1_{z}} \right) \left( \frac{1}{\sqrt{2}} ( \ket{0_{y}}+\ket{1_{y}} ) \right) \left( \frac{1}{\sqrt{2}} ( \ket{0_{x}}+\ket{1_{x}} ) \right) \\ &= \frac{1}{2} \left( \ket{1_{z}} \ket{0_{y}} \ket{0_{x}} + \ket{1_{z}} \ket{0_{y}} \ket{1_{x}} + \ket{1_{z}} \ket{1_{y}} \ket{0_{x}} + \ket{1_{z}} \ket{1_{y}} \ket{1_{x}} \right) \\ &= \frac{1}{2} (\ket{100}+\ket{101}+\ket{110}+\ket{111}) \end{align}

と，終状態の状態ベクトルを計算することができます。
念の為，測定後に $\ket{100}$ 状態が得られる確率を計算してみると

\begin{align} P_{\ket{100}} &= \braket{100 | \Psi '}^2 \\ &= \braket{100| \frac{1}{2} \bigl(\ket{100}+\ket{101}+\ket{110}+\ket{111} \bigr) }^2　\\ &= \bigl( \frac{1}{2} \braket{100|100} \bigr)^2 \\ &= (\frac{1}{2})^2 (\braket{100|100})^2 \\ &= \frac{1}{4} \\ \end{align}

となり， $\ket{100}$ は$ \frac{1}{4}$の確率で測定されることが分かります😋
他の状態についても同様の計算で測定確率を導くことができ，いずれの状態も $\frac{1}{4}$ の確率で検出されることが分かります。
実際に確率的に検出される量子力学の測定において1024回試行すると厳密に $\frac{1}{4}$ ，つまり256回ずつの検出回数とはならず，上記のヒストグラムのようなばらつきを含む結果となります😜

Q3-5.API

Hadamard on qiskit API ref

第4問は, 量子回路のmeasureの扱い方に関する問題です！

Q4.

Given an empty QuantumCircuit object, qc, with three qubits and three classical bits, which one of these code fragments would create this circuit?

[A]
qc.measure([0,1,2], [0,1,2])

[B]
qc.measure([0,0], [1,1], [2,2])

[C]
qc.measure_all()

[D]
qc.measure(0,1,2)

答え

[A]

Q4-1. 用語

測定については用語として扱わずに，下の背景partで述べます！

Q4-2. 背景

まず，量子力学における測定で注意することはなんでしょうか？？
代表的な注意点を3つあげてみましょう😅

測定が確率的である点

量子状態は複数取りうる状態がある時，それらが重なり合っている場合があります。その状態を測定した場合，各測定確率に応じて各々の状態が観測されます！

測定自体が(量子)状態を破壊しうる点

量子力学では，測定自体が重ね合わせ状態を破壊してある一つの状態に固定させてしまう場合があります。測定によって系が特定の状態に制約されるとも言えます。また数学的には，測定は非ユニタリ操作であり，測定後に測定前の状態に可逆的に戻すことはできません！

測定結果が観測者に依存しうる点

量子力学における測定は，観測者+量子状態がセットである点も重要です。観測者自身やその測定手段が異なる場合，測定される状態は変わります！

古典的な決定論的測定とは考え方が異なることを再認識しましょう！

これらの問題を解くにあたり，状態ベクトルにかかる係数の意味を改めて考えました。
例えば，

\begin{equation} \ket{\Psi} = \frac{1}{2} \left( \ket{0} + \sqrt{3} \ket{1}\right) \end{equation}

という状態が存在する場合， $\ket{0}$ が測定される確率は $\frac{1}{4}$ , $\ket{1}$ が測定される確率は $\frac{3}{4}$ となります。
上記のように状態ベクトル $\ket{\Psi}$ を書くと，ある比率で $\ket{0}$ と $\ket{1}$ の２つの状態が同時に存在しているかのように感じます。同時に存在するという考え方も正しいのですが，単に状態( $\ket{0}$ or $\ket{1}$ )が観測される確率振幅と考えるのも良いかと思います。両者ともに同じことを言っているかと思いますが，どちらかの納得する方で理解を進めるのも良いかと思います。私はこの辺りの考え方が，まだ納得感を持って説明できないのでさらに精進して理解を深めたいと思います！

Q4-3. 選択肢解説

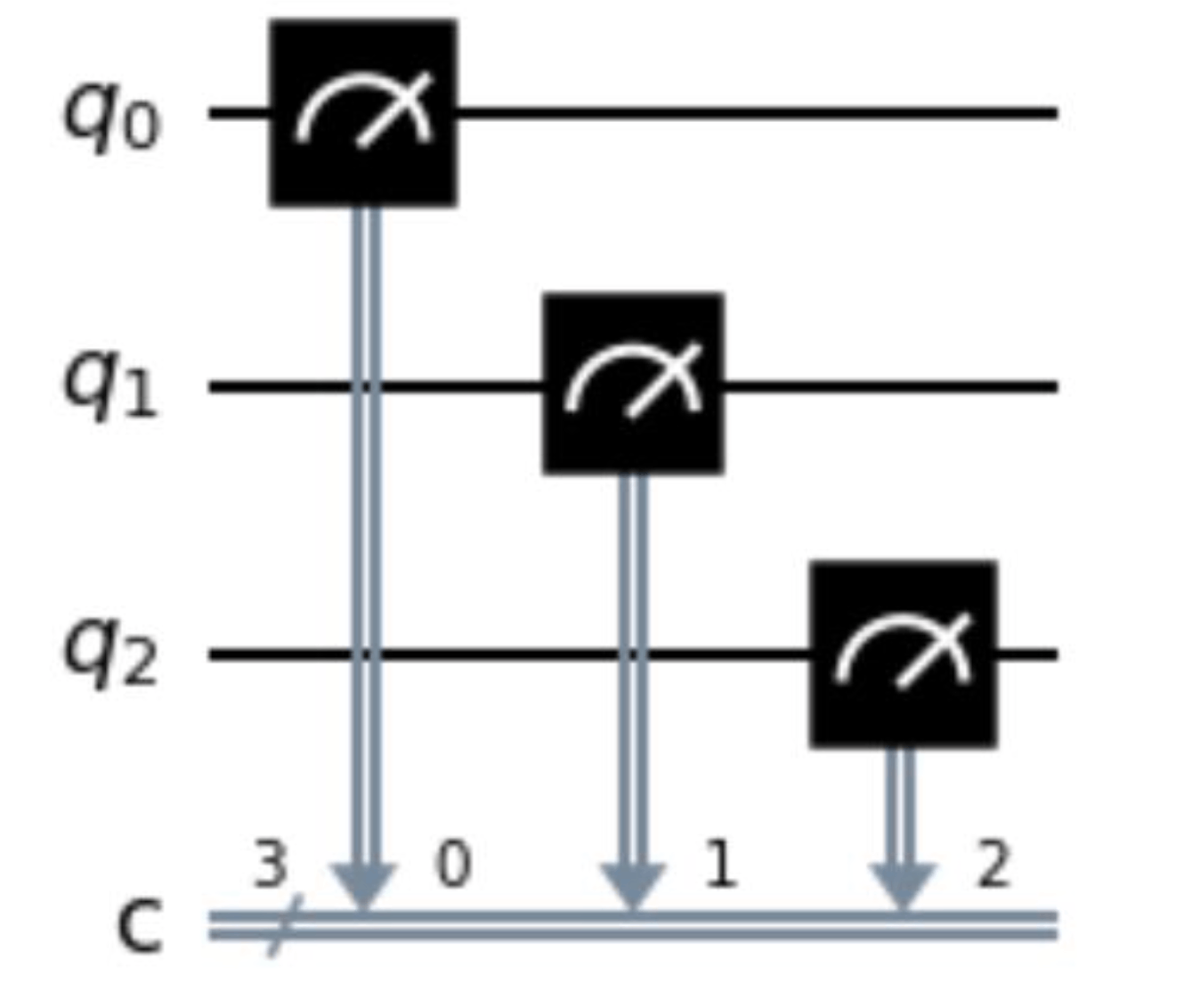
問題文でも述べられている通りですが，与えられた量子回路のキーとなる特徴は，

3つの量子ビットがある
3つの古典ビットがある
q0->c0, q1->c1, q2->c2 でそれぞれ測定される
の3点です。

qc.measureはqc.measure(qubit, cbit)のように，2つのパラメータを取り，測定を実行します。

[A]
qc.measure([0,1,2], [0,1,2])
これは，題意を満たしており，正解です😋

[B]
qc.measure([0,0], [1,1], [2,2])
3つのパラメータを取っているため，TypeErrorになってしまいます。そのため不正解です🙃

[C]
qc.measure_all()
qc.measure_all()は，新たに測定用のcbitを追加して測定結果を保存します。
また，qc.measre_all()は，測定前にBarrierを入れる仕様になっています。
与えられた回路では，古典ビットが既に3つ作成済みのため，新たに追加される分の古典ビットが多くなるため題意に沿わなくなってしまいます。そのため不正解です🙃
<img src="images/2023-06-05-22-53-30.png" width=300 height=300>

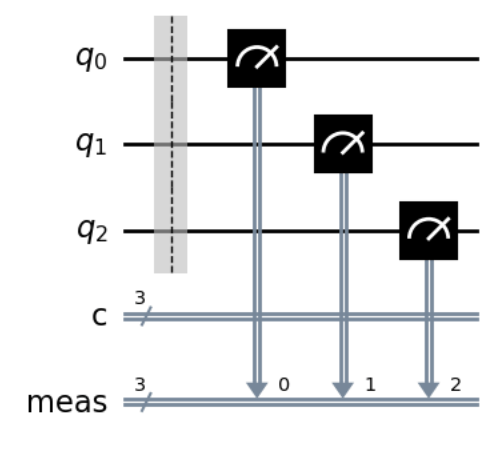
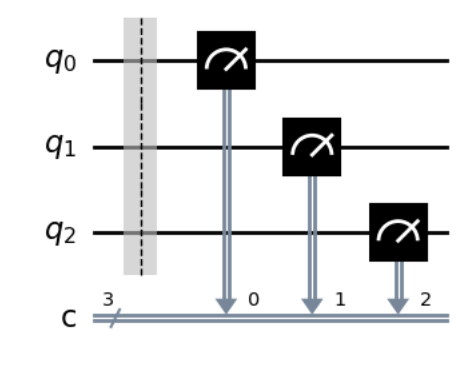
ちなみに，qc.measure_all()はparameterの指定の仕方で既存の古典ビットに測定を保存することができます！
その場合，qc.measure_all(add_bits=False)とします！
この場合も，測定前にbarrierが入るため，完全に一致はしませんが題意に近い回路設計になります。

[D]
qc.measure(0,1,2)
これも[B]同様，3つのパラメータを取っているため，TypeErrorになります！もち不正解です🙃

Q4-4. シミュレーション

今回シミュレーションすることは特にないため，Skipします！

次はエンタングル状態の作り方を問う問題です。
量子計算/情報通信の肝の部分なので，しっかり理解しましょう！

Q5

Which code fragment will produce a maximally entangled, or Bell, state?

[A]
bell = QuantumCircuit(2)
bell.h(0)
bell.x(1)
bell.cx(0, 1)

[B]
bell = QuantumCircuit(2)
bell.cx(0, 1)
bell.h(0)
bell.x(1)

[C]
bell = QuantumCircuit(2)
bell.h(0)
bell.x(1)
bell.cz(0, 1)

[D]
bell = QuantumCircuit(2)
bell.h(0)
bell.h(0)

答え

[A]

Q5-1.用語

エンタングルとベル状態について解説しましょう！量子計算の醍醐味ですね！
エンタングルとは，2つ以上の"量子ビット同士が従属している状態"を指します。とはいえ，"量子ビット同士が従属"?なんのこっちゃという感じですね。。。。解説が長くなるので，既に理解している人は飛ばして呼んでください🛩

私の場合は，"従属"の対義語である"独立"であること合わせて考えると納得感があり，理解することができました！まずはある２つの量子ビットが"独立である"場合の状態について深めていきましょう！

まず，"独立"とは"相手(他者)に影響を受けない，与えない"状態を指します。
経済的な"独立"や，アメリカ"独立"宣言など日常的な用語でも理解ができるかと思います！量子ビットの場合も同様です！
2つの量子ビットをそれぞれ $\ket{q_{0}}, \ket{q_{1}}$ としましょう！
そして，２つの量子ビットを合わせた量子状態を $\ket{\Psi}$ としましょう。

i.) それぞれの量子ビットが独立で単一の状態を持つ場合

仮に $\ket{q_{0}}$ は $\ket{0}$ , $\ket{q_1}$ が $\ket{0}$ の状態をとる場合，量子状態 $\ket{\Psi}$ は

\begin{align} \ket{\Psi} &= \ket{0_{q_{0}}} \otimes \ket{0_{q_{1}}} \\ &= \ket{0} \ket{0} \\ &= \ket{00} \end{align}

と表され，全体としての量子状態は唯一の状態 $\ket{00}$ を取ります。
それぞれ１つの状態しか取らないので全体としても１つの状態となるのは，理解しやすいかと思います。
では，どちらかが2つの量子状態を持つ場合はどうなるでしょうか？

ii.) 1方が1状態，他方が2状態の重ね合わせの場合

次に, $\ket{q_{0}}=\ket{0}$ , $\ket{q_{1}}= \frac{1}{\sqrt{2}} \left( \ket{0} + \ket{1} \right)$ をとる場合を考えてみましょう！ $\ket{q_{0}}$ はi.) と同様に唯一の状態を取りますが， $\ket{q_{1}}$ は2状態が重ね合わせられており，測定した場合 $\frac{1}{2}$ の確率でそれぞれ $\ket{0}, \ket{1}$ が測定される状態です。ただし， $\ket{q_{0}}$ と $\ket{q_{1}}$ は独立であり，それぞれに影響を与えることはありません。このとき，全体としての量子状態 $\ket{\Psi}$ はどうなるでしょうか？？シンプルに考えると，

$\ket{q_{0}}$ が $\ket{0}$ で $\ket{q_{1}}$ が $\ket{0}$
$\ket{q_{0}}$ が $\ket{0}$ で $\ket{q_{1}}$ が $\ket{1}$

の2状態があり得そうですね！これは，それぞれが独立であれば，起こりうる事象は積事象として表されることから，計算で導出することができます。これが量子力学で耳にする"直積"状態です。簡単ですが計算して確かめてみましょう！

\begin{align} \ket{\Psi} &= \ket{q_{0}} \otimes \ket{q_{1}} \\ &= \ket{0_{q_{0}}} \otimes \frac{1}{\sqrt{2}} \left( \ket{0_{q_{1}} + \ket{1_{q_{1}}}} \right) \\ &= \frac{1}{\sqrt{2}} \left( \ket{0_{q_{0}}} \otimes \ket{0_{q_{1}}} + \ket{0_{q_{0}}} \otimes \ket{1_{q_{1}}} \right)　\\ &= \frac{1}{\sqrt{2}} \left( \ket{0_{q_{0}}} \ket{0_{q_{1}}} + \ket{0_{q_{0}}} \ket{1_{q_{1}}} \right) \\ &= \frac{1}{\sqrt{2}} \left( \ket{0_{q_{0}} {0_{q_{1}}}} + \ket{0_{q_{0}} 1_{q_{1}}} \right) \\ &= \frac{1}{\sqrt{2}} \left( \ket{00} + \ket{01} \right) \\ \end{align}

この積事象(直積)の計算から，上記の2状態となることが分かります！
重要なことなのでもう一度書きますが，上記のように積事象(直積)で表されるのは，２つの状態が独立であるからです！

結局エンタングルとは何なのか？

エンタングル状態では，上記のようにそれぞれの量子ビットが独立ではなく，従属関係にある状態を指します。つまり，直積状態で表現できない状態がエンタングルメント状態と言えます。
２量子ビットが直積で表すことのできる状態は全部で7種類です！
計算しながら確認してみましょう！

\begin{align} \ket{\Psi_{0}} &= \ket{0_{q_{0}}} \otimes \ket{0_{q_{1}}} \\ &= \ket{0_{q_{0}}} \ket{0_{q_{1}}} \nonumber \\ &= \ket{00} \\ \nonumber \\ \ket{\Psi_{1}} &= \ket{1_{q_{0}}} \otimes \ket{1_{q_{1}}} \\ &= \ket{1_{q_{0}}} \ket{1_{q_{1}}} \nonumber \\ &= \ket{11} \\ \nonumber \\ \ket{\Psi_{2}} &= \ket{0_{q_{0}}} \otimes \left( \gamma \ket{0_{q_{1}}} + \delta \ket{1_{q_{1}}} \right) \\ &= \gamma \ket{0_{q_{0}}} \ket{0_{q_{1}}} + \delta \ket{0_{q_{0}}} \ket{1_{q_{1}}} \nonumber \\ &= \gamma \ket{00} + \delta \ket{01}\\ \nonumber \\ \ket{\Psi_{3}} &= \ket{1_{q_{0}}} \otimes \left( \gamma \ket{0_{q_{1}}} + \delta \ket{1_{q_{1}}} \right) \\ &= \gamma \ket{1_{q_{0}}} \ket{0_{q_{1}}} + \delta \ket{1_{q_{0}}} \ket{1_{q_{1}}} \nonumber \\ &= \gamma \ket{10} + \delta \ket{11} \\ \nonumber \\ \ket{\Psi_{4}} &= \left( \alpha \ket{0_{q_{0}}} + \beta \ket {1_{q_{0}}} \right) \otimes \ket{0_{q_{1}}} \\ &= \alpha \ket{0_{q_{0}}} \ket{0_{q_{1}}} + \beta \ket{1_{q_{0}}} \ket{0_{q_{1}}} \nonumber \\ &= \alpha \ket{00} + \beta \ket{10}\\ \nonumber \\ \ket{\Psi_{5}} &= \left( \alpha \ket{0_{q_{0}}} + \beta \ket{1_{q_{0}}} \right) \otimes \ket{1_{q_{1}}} \\ &= \alpha \ket{0_{q_{0}}} \ket{1_{q_{1}}} + \beta \ket{1_{q_{0}}} \ket{1_{q_{1}}} \nonumber \\ &= \alpha \ket{01} + \beta \ket{11} \\ \nonumber \\ \ket{\Psi_{6}} &= \left( \alpha \ket{0_{q_{0}}} + \beta \ket{1_{q_{0}}} \right) \otimes \left( \gamma \ket{0_{q_{1}}} + \delta \ket{1_{q_{1}}} \right) \\ &= \alpha \gamma \ket{0_{q_{0}}} \ket{0_{q_{1}}} + \beta \gamma \ket{1_{q_{0}}} \ket{0_{q_{1}}} + \alpha \delta \ket{0_{q_{0}}} \ket{1_{q_{1}}} + \beta \delta \ket{1_{q_{0}}} \ket{1_{q_{1}}} \nonumber \\ &= \alpha \gamma \ket{00}+ \beta \gamma \ket{01}+ \alpha \delta \ket{10} + \beta \delta \ket{11}\\ \end{align}

それでは，エンタングル状態の例を用いて考えます。
たとえば，ベル状態は以下です。

\begin{align} \ket{\Phi^{+}} = \frac{1}{\sqrt{2}} \left( \ket{00} + \ket{11} \right) \\ \ket{\Phi^{-}} = \frac{1}{\sqrt{2}} \left( \ket{00} - \ket{11} \right) \\ \ket{\Psi^{+}} = \frac{1}{\sqrt{2}} \left( \ket{01} + \ket{10} \right) \\ \ket{\Psi^{-}} = \frac{1}{\sqrt{2}} \left( \ket{01} - \ket{10} \right) \\ \end{align}

直積状態で表すことのできる状態の組み合わせの中に，ベル状態の4状態は含まれないことが分かります。つまり，ベル状態は2量子ビットの直積で表すことができない,つまりお互いに従属した関係であると言えます。これがエンタングル状態の本質です！

Q5-2. 背景

今回の問題はいかにベル状態を作るかの問題です！
問題文に制御NOT, 制御Zゲートが出てくるのでそれぞれどういう性質を持つゲートなのかについて解説したいと思います！

量子状態ベクトル表現の定義

初期状態を $\ket{\Psi_{0}}$ , 終状態を $\ket{\Psi_{1}}$ とします！
また，状態ベクトルの各要素は

\begin{align} \ket{\Psi} &= \begin{pmatrix} c_{00}:\ket{0_{t}0_{c}}の確率振幅 \\ c_{10}:\ket{1_{t}0_{c}}の確率振幅 \\ c_{01}:\ket{0_{t}1_{c}}の確率振幅 \\ c_{11}:\ket{1_{t}1_{c}}の確率振幅 \\ \end{pmatrix} \\ \end{align}

とします。
$\hat{CX}$ :CNOT(制御NOT)ゲート, $\hat{CZ}$ :CZゲートは以下の通りです！

制御NOTゲート

制御NOTゲートは
①Contolビットが $\ket{0}$ のときは,Targetビットには何もせず,
②Controlビットが $\ket{1}$ のときは,Targetビットの状態を反転させる
ゲートです。
まずはディラック表示では下記のように表現されます！
それぞれ添字がついていますが，tはTarget, cはControlを表しています。

\begin{align} \hat{CX} &= \Bigl( \ket{0}_t \bra{0}_t + \ket{1}_t \bra{1}_t \Bigr) \otimes \Bigl( \ket{0_c} \bra{0_c} \Bigr) + \Bigl( \ket{1}_t \bra{0}_t + \ket{0}_t \bra{1}_t \Bigr) \otimes \Bigl( \ket{1}_c \bra{1}_c \Bigr) \\ &=\ket{00} \bra{00} + \ket{10} \bra{10} + \ket{11} \bra{01} + \ket{01} \bra{11} \end{align}

これを行列表現にすると

\begin{align} \hat{CX} = \left( \begin{matrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 1 \\ 0 & 0 & 1 & 0 \\ \end{matrix} \right) \\ \end{align}

として表されます。
試しに，初期状態 $\ket{{\Psi_0}}$ として下記のように定義して， $\hat{CX}$ を作用させると

\begin{align} \ket{\Psi_{0}} &= \left( \begin{matrix} c_{00} \\ c_{10} \\ c_{01} \\ c_{11} \end{matrix} \right) \\ & = c_{00} \ket{0}_t \otimes \ket{0}_c + c_{10} \ket{1}_t \otimes \ket{0}_c + c_{01} \ket{1}_t \otimes \ket{0}_c + c_{11} \ket{1}_t \otimes \ket{1}_c \\ & = c_{00} \ket{00}+ c_{10} \ket{10} + c_{01} \ket{01} + c_{11} \ket{11}\\ \ket{\Psi'} &= \hat{CX} \ket{\Psi_0} \\ &= c_{00} \ket{00}+ c_{10} \ket{10} + c_{01} \ket{11} + c_{11} \ket{01}\\ \end{align} \\

となり， $\ket{01}$ と $\ket{11}$ 状態の確率振幅が入れ替わることが確認できます！

制御Z(位相反転)ゲート

また，制御Zゲートは，
①Contolビットが $\ket{0}$ のときは, Targetビットには何もせず,
②Controlビットが $\ket{1}$ のときは，Targetビットの位相を反転させる
ゲートです！
制御Zゲートの行列，ディラック表現は下記のようになります！

\hat{CZ} = \Bigl( \ket{0}_t \bra{0}_t + \ket{1}_t \bra{1}_t \Bigr) \ket{0}_c + \Bigl( \ket{0}_t \bra{0}_t + e^{\pi}\ket{1}_t \bra{1}_t \Bigr) \ket{1}_c \bra{1}_c

これを行列表現にすると，

\begin{align} \hat{CZ} = \left( \begin{matrix} +1 & 0 & 0 & 0 \\ 0 & +1 & 0 & 0 \\ 0 & 0 & +1 & 0 \\ 0 & 0 & 0 & +e^{\pi} \\ \end{matrix} \right)\\ \end{align}

と表されます。
$\hat{CX}$ の時と同様に，ベクトル $\ket{\Psi_{0}}$ に作用させると

\begin{align} \ket{\Psi'} &= \hat{CZ} \ket{\Psi_{0}} \\ &= c_{00} \ket{00}+ c_{10} \ket{10} + c_{01}\ket{01} +e^{\pi}c_{11} \ket{11}\\ &= c_{00} \ket{00}+ c_{10} \ket{10} + c_{01}\ket{01} -c_{11} \ket{11}\\ \end{align}

となり， $\ket{11}$ の符合が反転(位相が $\pi$ 回転)することを確認できます！

Q5-3. 選択肢解説

各設問の量子操作後の終状態を計算してみましょう。

[A]
下記の計算が実行されます！そんなに難しくないので，冗長に感じるかもしれませんが耐えましょう！
まず， $\ket{q_{0}}$ , $\ket{q_{1}}$ のそれぞれに対して独立にアダマールゲート，NOTゲートが適用されます！

\begin{align} \ket{q_{0}'} &= \hat{H} \ket{0}_{q_{0}} \\ &= \frac{1}{\sqrt{2}} (\ket{0}_{q_{0}} + \ket{1}_{q_{0}}) \\ \ket{q_{1}'} &= \hat{X} \ket{0}_{q_{1}} \\ &= \ket{1}_{q_{1}} \end{align}

次にCNOTゲートが適用されるため， $\ket{q_{0}}, \ket{q_{1}}$ を直積状態にして表現したのちに，CNOTゲートを適用するの
ので下記の計算してみましょう！すると，

\begin{align} \ket{\Psi'} &= \ket{q'_{1}} \otimes \ket{q'_{0}} \\ &= \frac{1}{\sqrt{2}} (\ket{10}+\ket{11}) \\ \end{align}

CNOTゲートを適用すると

\begin{align} \hat{CNOT_{q_{0}, q_{1}}} \ket{\Psi'} &= \frac{1}{\sqrt{2}} (\ket{10} + \ket{01}) \end{align}

となることが分かります。これは，直積状態で作ることができない状態でエンタングルしていると言えます。よって，正解となります😋
また，それぞれの確率振幅からそれぞれの状態は等しい確率で測定されることが分かりますね！

[B]
どんどん計算していきましょう！

\begin{align} \ket{\Psi'} &= \ket{0}_{q_{0}} \otimes \ket{0}_{q_{0}} \\ &= \ket{00} \\ \end{align}

CNOTゲートを適用すると

\begin{align} \hat{CNOT}_{q_{0},q_{1}} \ket{\Psi'} &= \ket{00} \\ \hat{X}_{q_{1}} \hat{H}_{q_{0}} \ket{\Psi'} &= \frac{1}{\sqrt{2}} ( \ket{11} + \ket{10} ) \\ \end{align}

この結果から，終状態は $\ket{11}, \ket{10}$ の2種類となり，これらは直積で表現できる状態です。つまり，それぞれは独立の状態と言えエンタングルしていないと言えます。そのため，題意を満たさず不正解となります🙃

[C]
どんどん行きましょう！

\begin{align} \ket{q_{0}'} &= \hat{H} \ket{0}_{q_{0}} \\ &= \frac{1}{\sqrt{2}} (\ket{0}_{q_{0}} + \ket{1}_{q_{0}}) \\ \ket{q_{1}'} &= \hat{X} \ket{0}_{q_{1}} \\ &= \ket{1}_{q_{1}} \\ \ket{\Psi'} &= \ket{q'_{1}} \otimes \ket{q'_{0}} \\ &= \frac{1}{\sqrt{2}} (\ket{10}+\ket{11}) \\ \end{align}

ここに $CZ$ ゲートを適用すると

\hat{CZ}_{q_{0}, q_{1}} \ket{\Psi'} = \frac{1}{\sqrt{2}} ( \ket{10} - \ket{11})

となります。これは選択肢[B]と同様に直積で表現できる状態のためエンタングルしていないと言えません。そのため，題意を満たさず不正解となります🙃

[D]
ラスト！ファイトです！

\begin{align} \ket{q_{0}'} &= \hat{H} \ket{0}_{q_{0}} \\ &= \frac{1}{\sqrt{2}} (\ket{0}_{q_{0}} + \ket{1}_{q_{0}}) \\ \ket{q_{0}''} &= \hat{H} \frac{1}{\sqrt{2}}( \ket{0}_{q_{0}} + \ket{1}_{q_{0}} ) \\ &= \frac{1}{2} \Bigl( (\ket{0}_{q_{0}}+ \ket{1}_{q_{0}}) + (\ket{0}_{q_{0}} - \ket{1}_{q_{1}}) \Bigr) \\ &= \ket{0}_{q_{0}} \\ \ket{\Psi'} &= \ket{q_{1}} \otimes \ket{q''_{0}} \\ &=\ket{0}_{q_{1}} \otimes \ket{0}_{q''_{0}} \\ &= \ket{00} \end{align}

となります。この結果は，最後は $\ket{00}$ の唯一の状態となります！これはもちろん題意を満たさず不正解となります🙃

Q5-4.シミュレーション

Aer Simulatorでそれぞれの測定頻度をPlotしてみましょう！

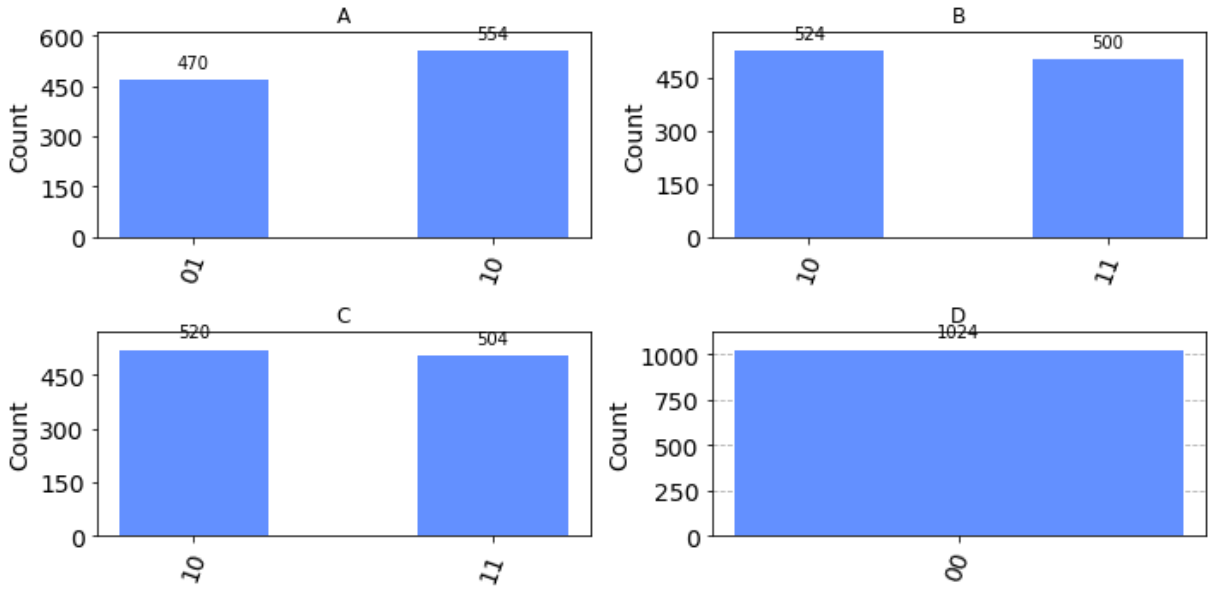
上記の結果の通り， $\ket{q_{0}} \otimes \ket{q_{1}}$ の直積状態で表されるのは,
選択肢の[A]のみですね！

ちなみに[B], [C]は $\left( \ket{1} \otimes \frac{1}{\sqrt{2}} (\ket{0} + \ket{1}) \right)$ , [D]は $\left( \ket{0} \otimes \ket{0} \right)$ の直積で表すことができるため，エンタングル状態ではありません。[A]のみ直積では表すことができないため，エンタングルしていると言えるのです🤔
これは，上記で手計算でじっくり計算した結果と測定確率は合致していることが確認できますね！

Q5-5. API

QuantumCircuit.cx
私は毎度, 第1, 2にどちらの量子ビットを入れるかを混同してしまいます💦紛らわしいですが，第1因数に制御ビット，第2因数にターゲットビットを設定します。ここで覚えてしまいましょう！

次は，ブロッホ球上の状態ベクトルの回転に関する問題です！

Q6

Given this code, which two inserted code fragments result in the state vector represented by this Bloch sphere?

  qc = QuantumCircuit(1,1)
  # Insert code fragment here
  simulator = Aer.get_backend('statevector_simulator')  
  job = execute(qc, simulator)  
  result = job.result()  
  outputstate = result.get_statevector(qc)  
  plot_bloch_multivector(outputstate)

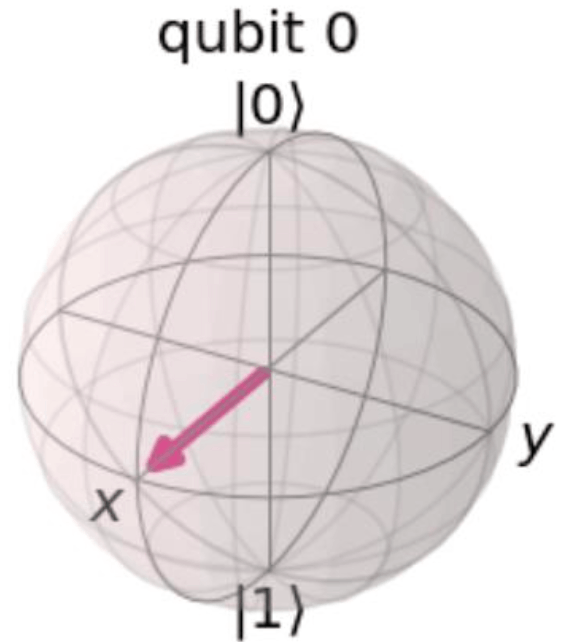
[A]
qc.h(0)

[B]
qc.rx(math.pi / 2, 0)

[C]
qc.ry(math.pi / 2, 0)

[D]
qc.rx(math.pi / 2, 0)
qc.rz(-math.pi / 2, 0)

[E]
qc.ry(math.pi, 0)

答え

[A], [C]

Q6.1 用語

rxゲート,ryゲート, rzゲートはそれぞれX,Y,Z軸周りの回転する単一量子ビットゲートです！

Q6.2 背景

今回の背景では，ブロッホ級上のベクトルの回転について考えたいと思います！
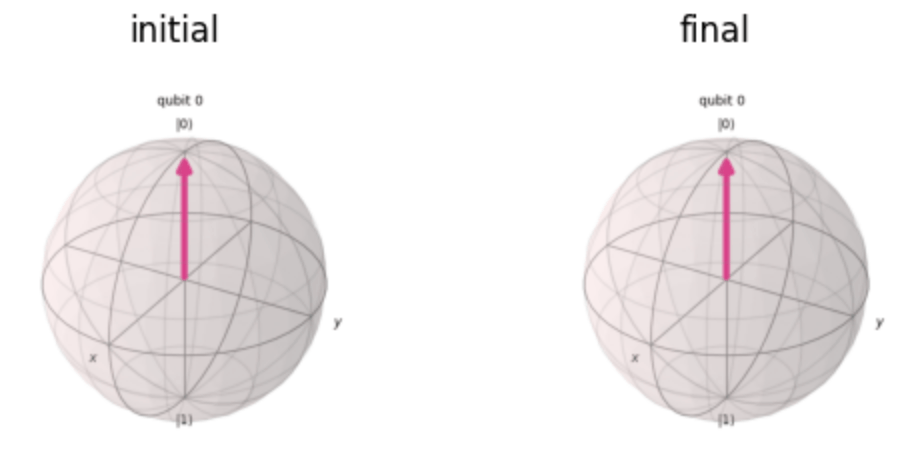
X軸周りの回転とは，X軸の正方向にネジが進むように回す方向をいい，もちろん他の軸周りでも同様です！それぞれの軸周りに $\frac{\pi}{2}$ 回転させて場合の状態ベクトルを下記に示します！

X軸回りの $\frac{\pi}{2}$ 回転

回転後は,Y軸の負方向に倒れたベクトルとなることが分かりますね！

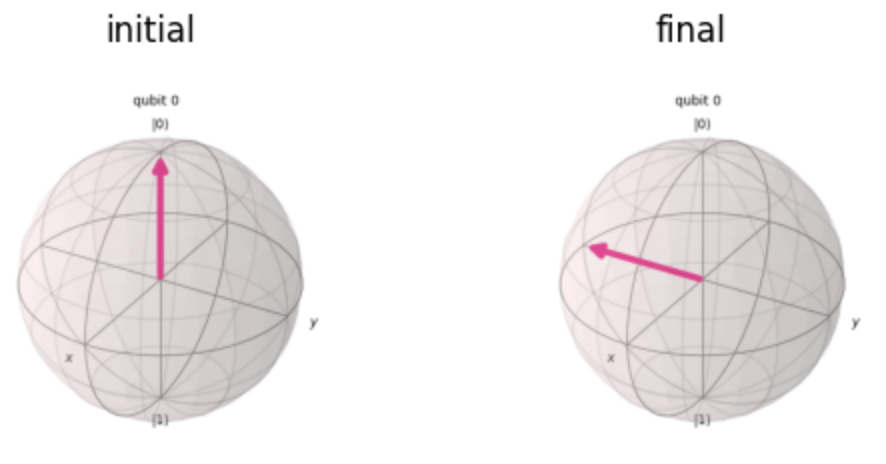
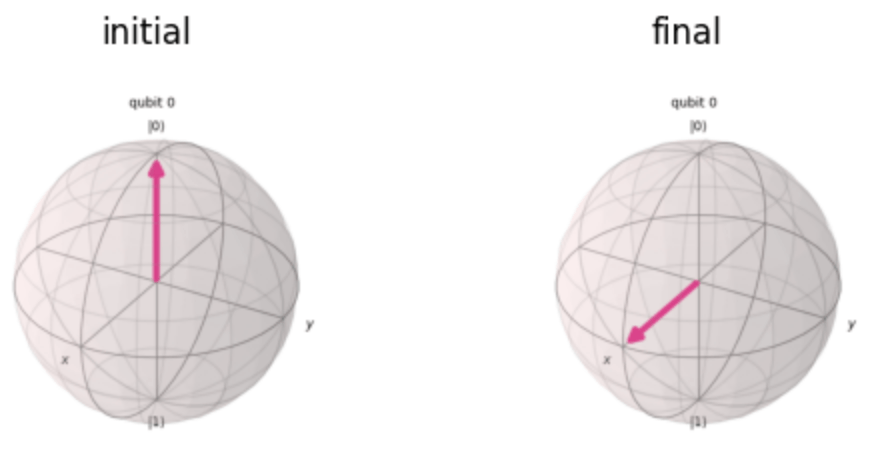
Y軸周りの $\frac{\pi}{2}$ 回転

回転後は,X軸の正方向に倒れたベクトルとなることが分かりますね！

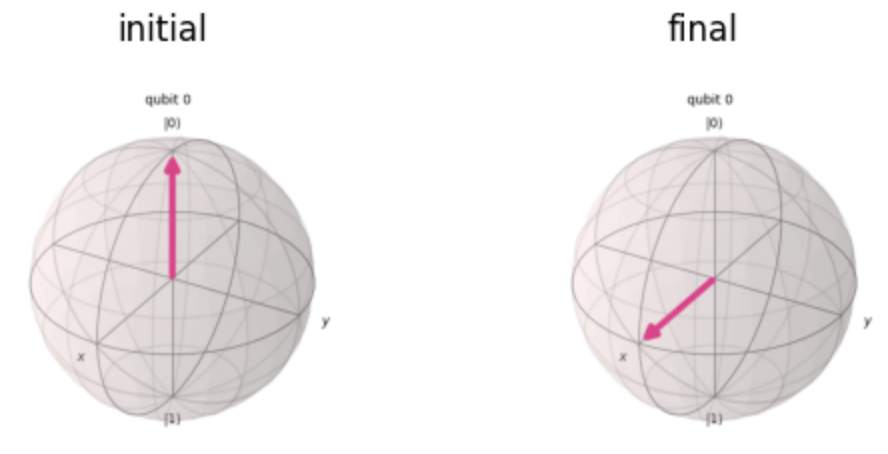
Z軸周りの $\frac{\pi}{2}$ 回転

Z軸上の状態ベクトルは，Z軸回りに回転させても同じ位置にいるため，
見かけ上回転していないように見えます！

Q6.3 選択肢解説

各選択肢のユニタリ操作後の状態ベクトルを下記に示します！
問題文で示されている状態は， $\ket{+X}=\frac{1}{\sqrt{2}} ( \ket{0} + \ket{1} )$ です！これは，回転軸と角度からわかる通り， $\ket{0}$ からY軸周りに $\frac{\pi}{2}$ 回転させることで得られることが分かります！
また，これはアダマール変換とも等価です！

選択肢[A]はアダマール変換のため，題意を満たし正解です😋
アダマール変換後の状態ベクトルは

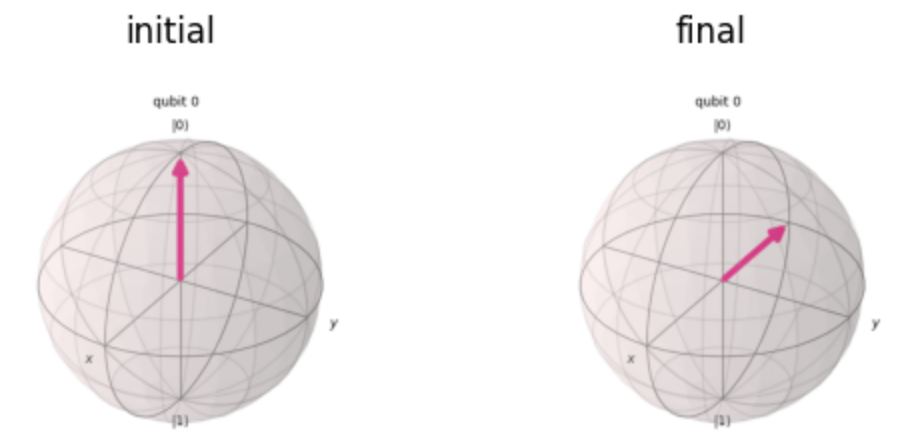
選択肢[B]は背景で解説したX軸周りの $\frac{\pi}{2}$ の回転と同じです！
これは題意に反するため，不正解です🙃

選択肢[C]は背景で解説したY軸周りの $\frac{\pi}{2}$ の回転と同じです！
これは，題意を満たすため正解です😋

選択肢[D]は下記のようになります！これは題意に反するため不正解です🙃

Q6.4 シミュレーション

今回は，上で状態ベクトルシミュレーションを実施しているため，
ここでの議論はSkipとさせていただきます！

Q6.5 Qiskit API

hadamard

次は位相ゲートに関する問題です！

Q7.

S-gate is a Qiskit phase gate with what value of the phase parameter?

[A]
π/4

[B]
π/2

[C]
π/8

[D]
π

答え

[B]

Q7.1 用語

Z軸周りの回転ゲートは位相ゲートと呼ばれており，それぞれ回転角度が $\frac{\pi}{2}, \frac{\pi}{4}$ には名称がついており，それぞれS, T ゲートと呼びます！
今回は，Sゲートのため，X軸周りの $\pi / 2$ の回転ゲートを示すものを選びます！

Q7.2 背景

そもそも位相ゲートとは何でしょうか？？
一言で言えば，量子的干渉の仕方が変得るために位相を変化させるゲートです！
量子的干渉は位相部のみで決まるものではありませんが，位相が変化すると周波数に応じた干渉の程度が変わり後の終状態に変化を与えます！

Q7.3 選択肢解説

選択肢は $\pi / 2$ である[B]のみが正解です😋

Q7.4 シミュレーション

特に今回はシミュレーションすることはないので，Skipします！

Q7.5 Qiskit API

APIも特にないので，skipします！

さて，つぎは状態ベクトルの出力に関する問題です！

Q8.

Which two code fragments, when inserted into the code below, will produce the statevector shown in the output?

from qiskit import QuantumCircuit, Aer, execute
from math import sqrt
qc = QuantumCircuit(2)  
# Insert fragment here  
simulator = Aer.get_backend('statevector_simulator')  
result = execute(qc, simulator).result()  
statevector = result.get_statevector()  
print(statevector)

Output:
[0.707+0.j 0.+0.j 0.+0.j 0.707+0.j]

[A]
v = [1/sqrt(2), 0, 0, 1/sqrt(2)]
qc.initialize(v,[0,1])

[B]
qc.h(0)
qc.cx(0,1)

[C]
v1, v2 = [1,0], [0,1]
qc.initialize(v1,0)
qc.initialize(v2,1)

[D]　　
qc.cx(0,1)
qc.measure_all()

[E]
qc.h(0)
qc.h(1)
qc.measure_all()

答え

[A], [B]

Q8.2 背景

何度も出てくるので覚えておいた方がいい数字が0.707！
これは $\frac{1}{\sqrt{2}}$ です！
つまり，Outputで表現されているベクトルは

\begin{align} \ket{v} &= \left( \begin{matrix} \frac{1}{\sqrt{2}} \\ 0 \\ 0 \\ \frac{1}{\sqrt{2}} \\ \end{matrix} \right) \\ &= \frac{1}{\sqrt{2}} (\ket{00} + \ket{11}) \end{align}

となります！
上記のベクトルとなるゲートの組み合わせを探しましょう！

ちなみに，qc.initializeが初めて出てきたので，選択肢解説にいく前に使い方を解説しましょう！
第1引数には量子状態を指定するパラメータ，第2因数は量子レジスタを指定します。
この量子状態を指定するパラメータは主に3種類です！
i.) 文字列でパウリ行列の固有値を指定する方法
labelの中からstringで指定する
ii.) 数値のリストで確率振幅を指定する方法
iii.) 10進数を代入し，その2進数表現の量子状態を指す方法

Q8.3 選択肢解説

[A]
上記のパラメータの指定方法のii.)に該当する方法で，ベル状態を作っています！そのため題意を満たし正解となります😋

[B]
状態を計算すると下記のようになります。

\begin{align} \ket{v_{0}'} &= \hat{H} \ket{0}_{v_{0}} \\ &= \frac{1}{\sqrt{2}} (\ket{0}_{q_{0}} + \ket{1}_{v_{0}}) \\ \ket{q_{1}} &= \ket{1}_{v_{1}} \\ \ket{\Psi'} &= \ket{v_{1}} \otimes \ket{v'_{0}} \\ &= \frac{1}{\sqrt{2}} (\ket{00}+\ket{01}) \\ \end{align}

ここにCNOT(q0, q1)が適用され，

\begin{align} \hat{CNOT}_{v_{0},q_{1}} \ket{\Psi'} &= \frac{1}{\sqrt{2}} (\ket{00}+\ket{11}) \\ \end{align}

となります。これは $\ket{00}$ と $\ket{11}$ の振幅を $\frac{1}{\sqrt{2}}$ に設定しており，ベル状態となっています！これは，題意合致するため正解です😋

[C]
今回は上記のiii.)の方法で初期化されており, $\ket{v_{0}}, \ket{v_{1}}$ はそれぞれ $\ket{v_{0}}=\ket{0}, \ket{v_{1}}=\ket{1}$ で初期化されます！両方の直積として状態は $\ket{\Psi} = \ket{1} \otimes \ket{0} = \ket{10}$ となります！これは，題意に反するため不正解となります🙃

[D]
初期状態が $\ket{00}$ に対して，制御NOTで操作しても，状態は変わらないため，最終的な結果は $\ket{00}$ となります！
なので，不正解です🙃

[E]
ディラック表記で計算すると下記のようになります。

\begin{align} \ket{q_{0}} &= \hat{H} \ket{0}_{q_{0}} \\ &= \frac{1}{\sqrt{2}} ( \ket{0}_{q_{0}} + \ket{1}_{q_{0}})\\ \ket{q_{1}} &= \hat{H} \ket{0}_{q_{1}} \\ &= \frac{1}{\sqrt{2}} ( \ket{0}_{q_{1}} + \ket{1}_{q_{1}})\\ \ket{\Psi} &= \ket{q_{0}} \otimes \ket{q_{1}}\\ &= \frac{1}{2}(\ket{00}+\ket{10}+\ket{10}+\ket{11}) \end{align}

これも題意に反するため不正解です🙃

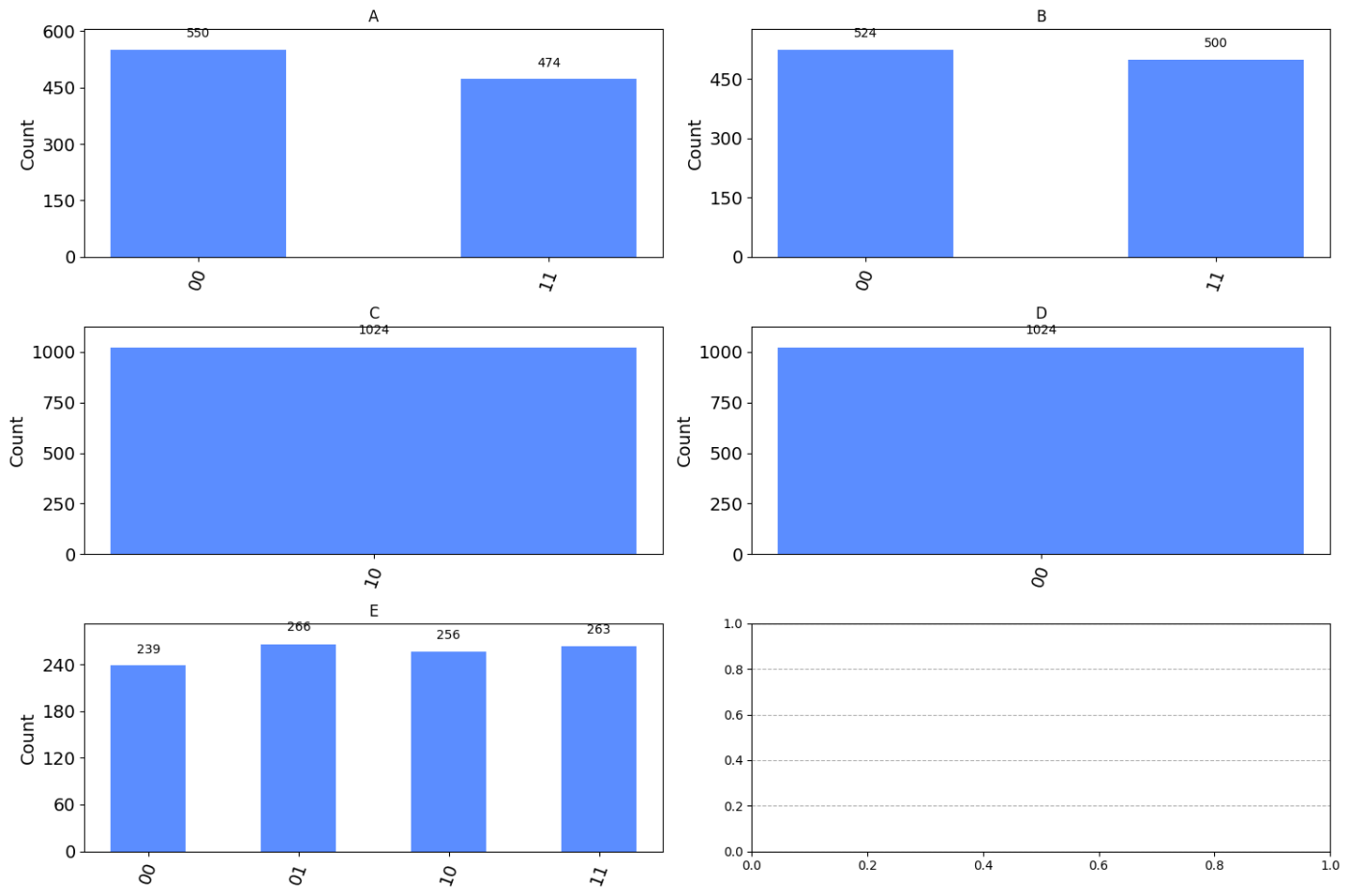
Q8.4 シミューレータ

選択肢の[A]~[E]のそれぞれの量子状態を測定した際のヒストグラムは下記の通りになります。上の計算通りの計測結果になってますね！

Q8.5 Qiskit API

qc.initialize

次はCNOT Gateの扱い方に関する問題です！

Q9.

Which code fragment will produce a multi-qubit gate other than a CNOT ?

[A]
qc.cx(0,1)

[B]
qc.cnot(0,1)

[C]
qc.mct([0],1)

[D]
qc.cz(0,1)

答え

[D]

Q9.1 用語

今まで出てきた用語ばかりですね！

Q9.2 背景

背景についても特にありません！

Q9.3 選択肢解説

methodで用意されている制御NOTのParametersは　qc.cx(control, target)の順で指定します！
選択肢[A], [B]で使用されているcx, cnot　methodは同じ使い方が可能で，正しい使い方であり正解です😋

選択肢[C]のように複数の制御ビットを持つNOT Gateを使いたい時は.mct methodも用意されています。qc.cxとの違いは，制御ビットを複数指定できる点です！第1因数としてリストを与えると，制御ビットとして用いるqubitを指定することができるのです！例えば，下記のように2つの制御ビットを持つ制御NOT(toffoli) Gateを作ることができます！

qc = QuantumCircuit(3)
qc.mct([0, 1], 2)
qc.draw()

ということで，これも正解になります😋

選択肢[D]は, Q5.で出てきたように制御ZGateは，制御ビットが1, かつTargetビットが1の時，そのTarget ビットの位相を反転させます。これは，CXゲートとは異なる操作になるため不正解です🙃

Q9.4 シミューレータ

今回はシミュレートすることは特にありません！

Q9.5 Qiskit API

qc.mct

さて次は，Toffoli Gateの使い方についての問題です！

Q10

Which code fragment will produce a multi-qubit gate other than a Toffoli?

[A]
qc.ccx(0,1,2)

[B]
qc.mct([0,1], 2)

[C]
from qiskit.circuit.library import CXGate
ccx = CXGate().control()
qc.append(ccx, [0,1,2])

[D]
qc.cry(0,1,2)

答え

[D]

Q10.1 用語

Toffoliゲートは，シンプルにはANDゲートの量子版です！
3つの量子ビットを操作するゲートであり，2つの制御量子ビットが1の状態のときのみ，3つめのTarget量子ビットにXゲートを適用します。

q0_control	q1_control	q2_target
0	0	0
0	1	0
1	0	0
1	1	1
0	0	1
0	1	1
1	0	1
1	1	0

Q10.2 背景

Toffoliゲートの使い所

Toffoliは量子計算のさまざまなアルゴリズムで使用されます！特に、量子エラー訂正など、誤り訂正や制御フローの実装などの応用で重要な役割を果たすようです(自分はまだ勉強中。。。)。また、Toffoliゲートは量子ビットの制御可能なユニバーサルセット（controlled-NOTゲートとHadamardゲートとの組み合わせ）の一部でもあります。

ユニバーサルセットについて

量子計算における量子操作を近似的に実現するために基本的なゲートのセットのことを言います。個セットによって，量子アルゴリズムの計算を実行するために必要な全ての操作を実現することができます。
具体的には以下の3つのゲートから構成されます。

任意の単一量子ビットゲート
CNOTゲート
1.2.の組み合わせ

toffoliゲートを単一量子ビットゲートとCNOTで表現すると下記のようになる。
(自分ではとても思いつきませんが，qiskit libraryに描いてもらうことができます。)

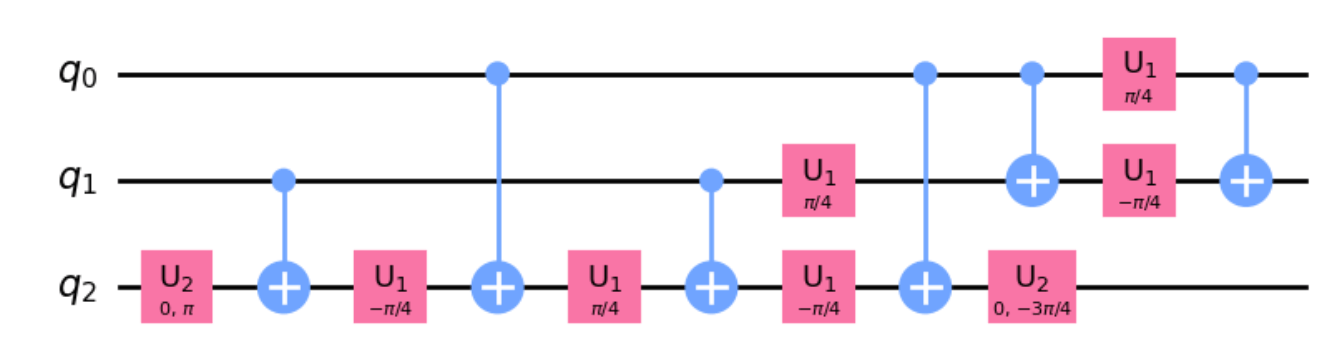
Q10.3 選択肢解説

[A]はQutumCircuit　classのccxメソッドに関する選択肢です。ccxメソッドはccx(q0, q1, target_bit)のように3つの量子ビットをparametersとしてとるのです。選択肢は
"0", "1", の量子ビットを制御ビット，"2"をターゲットビットとして指定できており題意を満たしており正解です😋

[B]はQutumCircuit classのmctメソッドに関する選択肢です。mctメソッドはmct(control_qbits,target_bit)をパラメータに取ります。control_qbitsはリストで指定することができるため，[B]は[A]同様，"0", "1", の量子ビットを制御ビット，"2"をターゲットビットとして指定できており題意を満たしているため正解です😋

[C]はCXGate classに関する選択肢です。CXGateはClassのため，制御NOTゲートのインスタンスを作る必要があります。自分でインスタンス化できる分，より柔軟にゲート設計できるのでしょうか...利点をよくわかっていません。。。
選択肢の書き方をもう少し書き下すと，下記のようになります。

cx = CXGate() #CXGateのインスタンスを作る
ccx = cx.control()  #CXGateのcontrolメソッドを使って，制御ビットを１つ増やしてCCXにする
qc.append(ccx, [0,1,2]) #量子回路qcにCCXゲートを追加する形で実装する。

qcのappendメソッドでCXを追加する場合，リストの末尾をTargetビットに指定します。
そのため，グラフに起こすと下記のようになります。

これは題意を満たしており，正解です😋

ちなみに，appendで渡す際に，[0,2,1]と指定すると，制御ビットが[q0,q2]でターゲットビットが[q1]として指定されます。

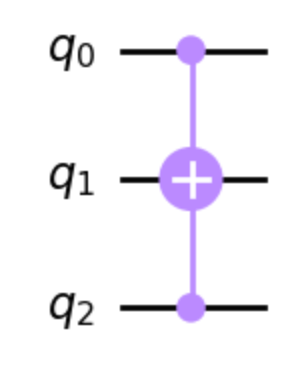
[D]はqc.cryメソッドに関する選択肢です！(theta, control_bit, target_bit)の順にParameterをとります！選択肢[D]のように指定すると，１番目のqbitが1の時にq2に0degのY軸方向の回転を加えることを意味しています！
これは，題意のようなToffoliゲートにはなり得えません！なので不正解です🙃

Q10.4 シミューレータ

今回もシミュレーションは特にないため，Skipします！

Q10.5 Qiskit API

qc.ccx