Zenn
🎣

【量子コンピュータ】IBM量子開発者認定試験(C1000-112)サンプル問題をしがんでしがんで舐め回す(後編 Q011-20)

2023/09/05に公開
Python
量子コンピュータ
qiskit
tech

みなさんこんにちは！
この記事は，IBMが提供する量子開発者認定資格試験 Exam C1000-112: Fundamentals of Quantum Computation Using Qiskit v0.2X Developerサンプル問題の解答と解説記事です！

今回は後編で，前編は下記ページにありますので，まだご覧になってない方は是非ご一読ください！
https://zenn.dev/whitishlion/articles/daff336619acef

前編で取り扱ったQ01.~Q10.の続きでQ11.~20を扱います。
では，早速解説の続きに進みたいと思います！

第11問は 量子回路の任意の部分をGroup化するbarrierの使い方に関する問題です！

Q11

Which two options would place a barrier across all qubits to the QuantumCircuit below?

  qc = QuantumCircuit(3,3)

[A]
qc.barrier(qc)

[B]
qc.barrier([0,1,2])

[C]
qc.barrier()

[D]
qc.barrier(3)

[E]
qc.barrier_all()

答え

[B], [C]

Q11.1 用語

QuantumCircuitのbarrierメソッドに関する設問です。さて，barrierとは一体なんでしょうか？barrierの語源は障壁や境界で，その名の通りある区間で量子回路を区切るための境界を作ることです。境界を作る目的は，量子回路の各操作や固まりをグループ化することができることです！詳細は, 背景partで解説します。

Q11.2 背景

量子ゲートの中には，複数の量子ゲートをまとめることができる場合ができます。例えば，複数の回転ゲートが作用する場合，Totalの回転角を操作する回転ゲート1回が作用していると考えることができます。

例えば，S行列操作を2回連続，T行列操作を1回操作させる回路を考えます。
それぞれの操作毎にbarrierを挟むと，それぞれの操作で区切られる。一方で，barrierを入れないとS行列2回による\pi回転とT行列の\frac{\pi}{4}の合計\frac{5 \pi}{4} = - \frac{3 \pi}{4}の1操作に集約されるのです。
量子ゲートを考える際に，１つ１つの操作を分けたいとき，ある領域でグループ化したい時には大変ありがたいツールです！
それぞれ図に起こすと下記のようになります！

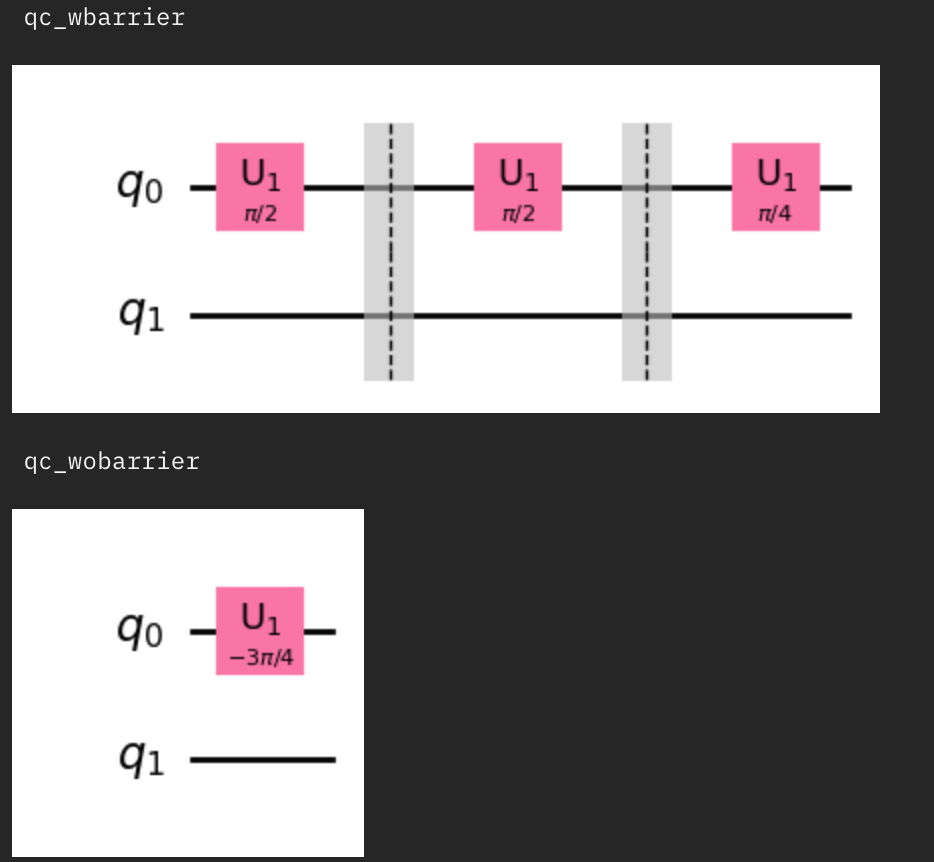
これは次のQ12でも関係してくるので覚えておきましょう！

Q11.3 選択肢解説

qc.barrier(num_qubits, label=None)の因数をとります。
barrierを入れたいタイミングは，qc.barrier()を挿入する場所で定義され
そのbarrierを入れる量子ビットを第1因数として指定します！

[A]のようにbarrierメソッドは量子回路をparameterとして取ることはありません！なのでエラーとなってしまいます！不正解です🙃

[B]のようにbarrierメソッドはqargsのパラメータを取ります。指定した量子ビットの番号にbarrierをかけることができます。これは題意を満たすため正解です😋

[C]のようにbarrierメソッドの因数に何も指定しないと，全ての量子ビットにbarrierが作用するため，題意を満たし正解となります😋

[D]のように量子ビットは3つしか準備していません。barrier(3)はq4を指定することとなり，準備されていない量子ビットを指定することになります。そのため，indexがout of rangeでエラーとなってしまうため不正解です🙃

[E]のようにqc.barrier_all()は使えそうですが，barrier_allというmethodはないのです。。。。なので不正解です🙃

Q11.4 シミューレータ

今回は特にシミュレートすることがないため，skipします！

Q11.5 Qiskit API

qc.barrier

次は　barrierの特性や使い所の理解に関する問題です！

Q12

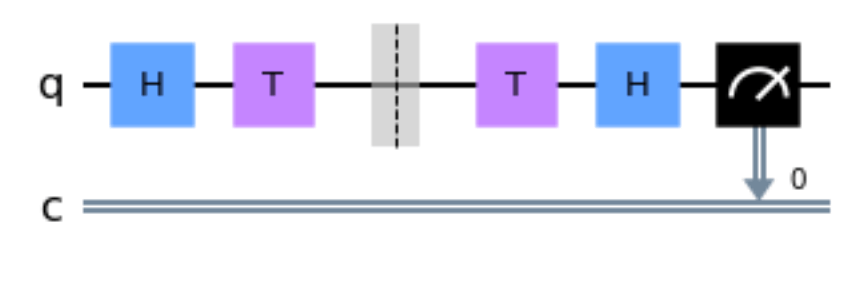
What code fragment codes the equivalent circuit if you remove the barrier in the following QuantumCircuit?

[A]
qc = QuantumCircuit(1,1)
qc.h(0)
qc.s(0)
qc.h(0)
qc.measure(0,0)

[B]
qc = QuantumCircuit(1,1)
qc.measure(0,0)

[C]
qc = QuantumCircuit(1,1)
qc.h(0)
qc.t(0)
qc.tdg(0)
qc.h(0)
qc.measure(0,0)

[D]
qc = QuantumCircuit(1,1)
qc.h(0)
qc.z(0)
qc.h(0)
qc.measure(0,0)

答え

[A]

Q12.1 用語

barrierの説明は，Q11で実施済みです！忘れてしまった方は，Q11をチェックしてみてください！

Q12.2 背景

背景もQ11と同じです！

Q12.3 選択肢解説

設問の量子回路には H -> T -> barrier -> T -> Hが作用しています！
Z軸方向に対する\frac{\pi}{4}回転(位相シフト)を表すT行列が二回作用しているため，barrierをなくすとその操作が1回の回転操作となり\frac{\pi}{2}の回転操作となります！\frac{\pi}{2}の回転操作はS行列で表されるため，H -> S -> Hの操作を実行している回路を表す選択肢が正解となります。1つ1つ探してみましょう！

[A]
H->S->Hの回転操作を表しており，題意を満たすため正解です😋

[B]は量子ビットと古典ビットを１つずつ用意して，測定しただけですね！
これらは題意の回路にはなり得ません🙃

[C]に見かけないメソッドが入っていますね！私も知りませんでしたのでチャジったところ，tdgメソッドはターゲット量子ビットにT^{\dag}を作用させるためのゲートだということがわかりました。ちなみにT^{\dag}はTゲートの逆位相を適用するゲートであり，-\frac{\pi}{4}の位相シフトゲートです。問題の回路からbarrierを取り去ってもこの回路にはならないため，不正解です！

[D]はH->Z->HでZゲートの回転角が0の場合のケースです。
回路は結構複雑な回転操作となり，下記のようにまとめられます。

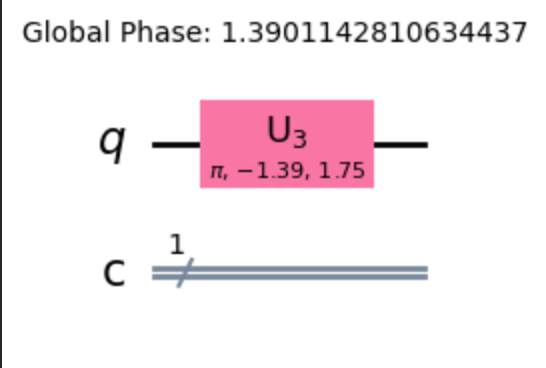
Q12.4 シミューレータ

問題文の回路とその回路を変換したときの回路図です。
このwo barrierと同じ状態となるゲートの組み合わせが正解になります！

全ての選択肢の回路図を表示してみます。
選択肢[A]

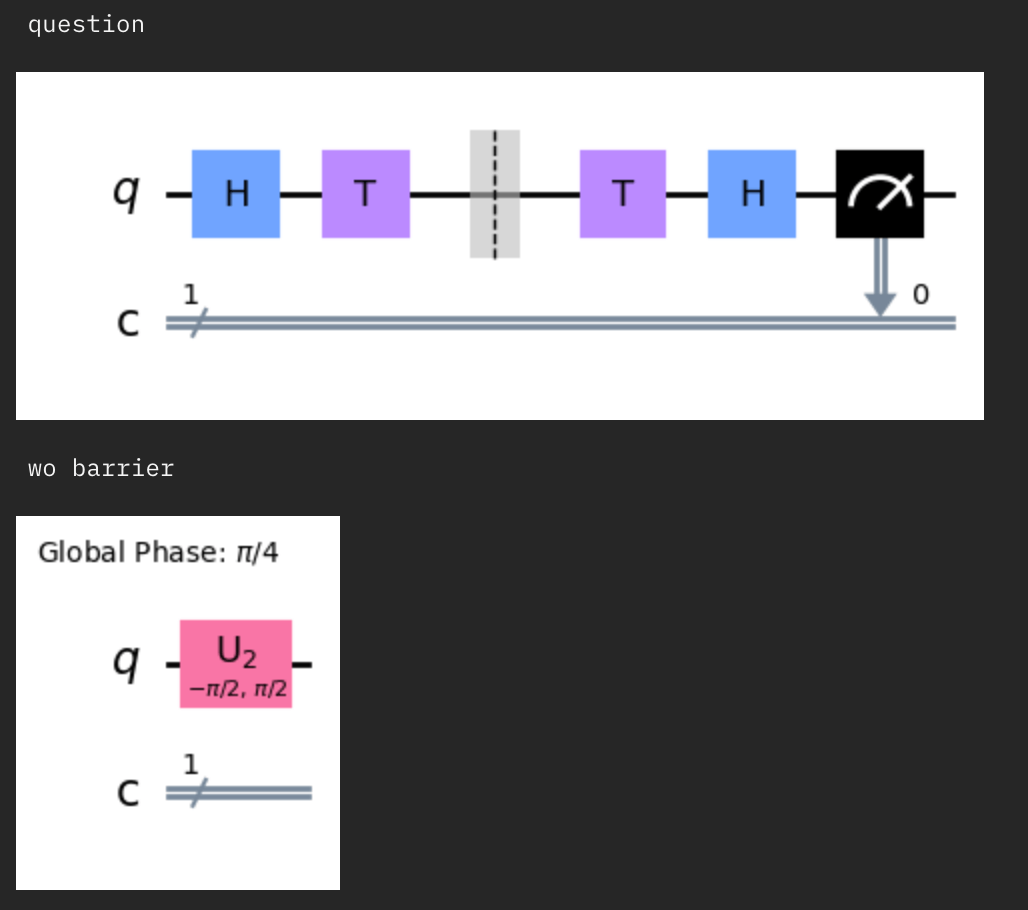
選択肢[C]

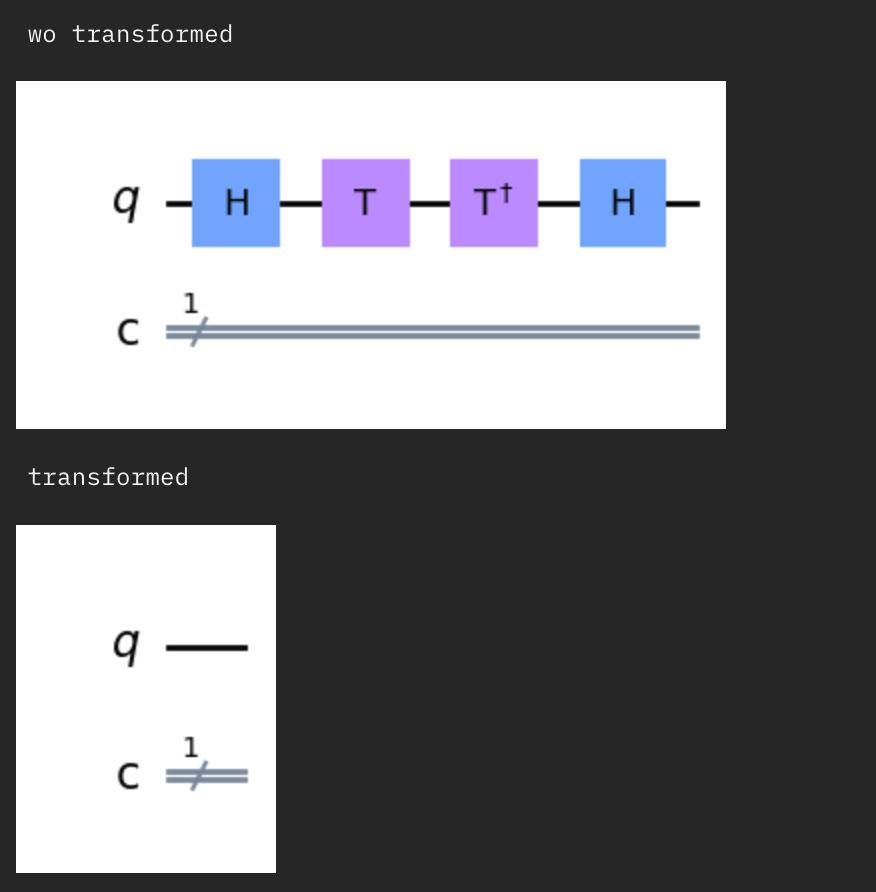
選択肢[D]

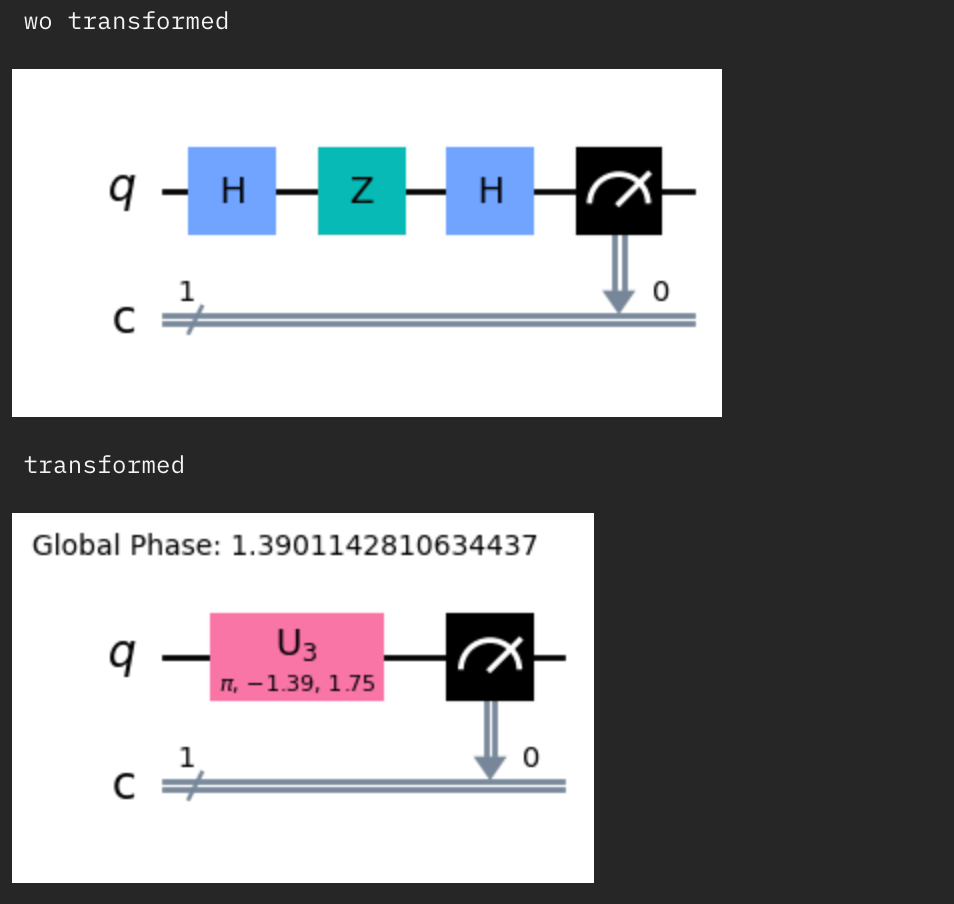
確かに選択肢Aの変換後の回路は問題文の回路と一致することが分かりますね！

Q12.5 Qiskit API

qc.tdg
tdgはTDaGgerのTDGということなのでしょう！

次は，量子回路の深さに関する問題です！

Q13

Given the following code, what is the depth of the circuit?

qc = QuantumCircuit(2, 2)
qc.h(0)
qc.barrier(0)
qc.cx(0,1)
qc.barrier([0,1])

[A]
2

[B]
3

[C]
4

[D]
5

答え

[A]

Q13.1 用語

depth (量子回路の深さ)は量子ゲート(操作)のレイヤー(階層)数を指します。
ビットに作用させる操作数を数えることと同じです！

Q13.2 背景

深さを知ると何が嬉しいのでしょうか？一般に量子ゲートが増えると，実行するのに必要なリソースが増えるため，実行するゲートの数を知ることは重要です。また，量子ビットは外乱影響に極めて敏感でエラーが生じやすいことが知られています。当然，量子操作が多いほどエラーの影響も受けやすいため，エラー訂正ビットの要件にもつながります。上記の理由から，所望の回路を構築する上で，「どれくらいの量子操作があり，どれだけの量子ビットを準備すべきか？」を検討するために，深さを知ることは重要な訳です！

Q13.3 選択肢解説

barrierは量子操作には入りません！
なので，今回は，最初のアダマールゲート，２番目の制御NOTゲート，合計２ゲートによる操作がおこなわれるため，深さは2と言えます。
そのため，答えは[A]の1択となります！

このように簡単な回路のDepthを知りたいことはまれで，大抵は深い階層をもつ場合や未知の場合の深さを知りたい場合が多いです。その際はQuautumCircuit classのメソッドからdepth methodを使って深さを求める方法を試してみましょう！

qc = QuantumCircuit(2, 2)
qc.h(0)
qc.barrier(0)
qc.cx(0,1)
qc.barrier([0,1])

print(qc.depth())

これを実行すると consoleに2が出力されることを確認することができます。

Q13.4 シミューレータ

今回はシミュレーションを使って，ユニタリ操作回数に応じて長くなる実行時間の傾向を可視化してみたいと思います！
回路としてやっていることはR_{y}(\theta=\frac{\pi}{6})をひたすら足していき，そのRy操作回数に応じた実行時間のplotです。

例えば，10回のUnitary操作をしている時の回路図は下記です。

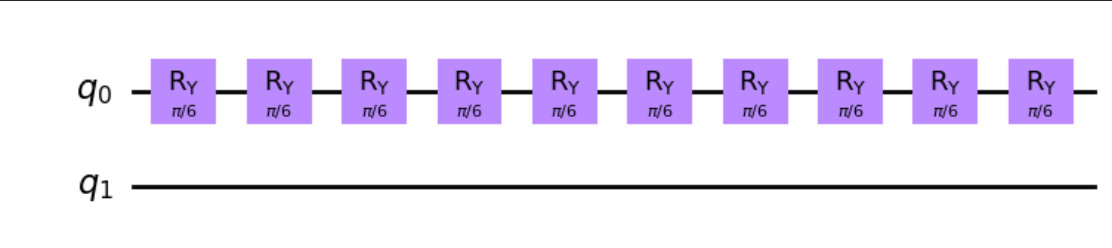
当たり前の結果ではありますが操作回数におおよそ比例して実行時間が増えることがわかります！

Q13.5 Qiskit API

qc.depth

次は，シミュレート実行の仕方とシミュレーション条件の指定の仕方に関する問題です！
特にcouplingについて学びながら解いてみましょう！

Q14

Which code snippet would execute a circuit given these parameters?

  1. Measure the circuit 1024 times,
  2. use the QASM simulator,
  3. use a coupling map that connects three qubits linearly
qc = QuantumCircuit(3)
# Insert code fragment here
result = job.result()

[A]
qasm_sim = Aer.get_backend('qasm_simulator')
couple_map = [ [0, 1], [1, 2] ]
job = execute(qc, backend=qasm_sim, shots=1024, coupling_map=couple_map)

[B]
qasm_sim = Aer.getBackend('ibmq_simulator')
couple_map = [ [0, 1], [0, 2] ]
job = execute(qc, loop=1024, coupling_map=couple_map)

[C]
qasm_sim = Aer.get_backend('qasm_simulator')
couple_map = [ [0, 1], [1, 2] ]
job = execute(qc, backend=qasm_sim, repeat=1024, coupling_map=couple_map)

[D]
qasm_sim = Aer.get_backend('qasm_simulator')
couple_map = [ [0, 1], [1, 2] ]
job = execute(backend=qasm_sim, qc, shot=1024, coupling_map=couple_map)

答え

[A]

Q14.1 用語

QASMはQuantum Assenbly Languageからもじったもので，QASM言語を使用して量子回路の動作をシミュレートするツールです!

次に，shotとはなんでしょうか？これはシミュレーション実行時のサンプリング回数を指定するためのオプションです！これまでの解説に出てきましたが，量子回路で測定される状態は確率的な性質を持ちます。そのため，全く同じ回路を実行したとしても，得られる結果が異なることは日常的に起こり得ます。そのため，結果に統計的な信頼性を持たせるために一定数以上のサンプリングを行います！量子測定においては，単一の測定では判断することはできず複数回の測定が必要です！その際のサンプリング数を指定します😆

最後にカップリングマップについて説明しましょう！
実際の量子デバイスでは，量子ビットがトポロジカルに配置されており，それぞれの量子ビットは一部の量子ビットと直接or間接的に繋がっています。量子回路におけるカップリングは，物理的な量子ビット間の接続性を表しており，量子ビット間の制御ゲートを適用する上で重要です。qiskitでは，transpileメソッドにcoupling_mapパラメータを指定することで，回路トランスパイル時に量子ビット同士の繋がり方を指定することができます！ちなみに非隣接量子ビット間の操作を実現するためにはSWAPゲートが必要になる場合がありますが，カップリングマップに基づいてコンパイラが自動で挿入してくれる場合があるらしいです。

Q14.2 背景

Couplingについて，もう少し深めてみましょう！
Couplingによって，量子ビット間の相互作用が発生します。相互作用とは，2つの量子ビットがどれほど情報を交換できるかとお互いに影響を与え合えるかの与えることです。
その必要性を簡単にまとめると, 以下の4点と言えます。

  1. エンタングルメントの生成
    上記でも説明したエンタングルメントに関してもCouplingが重要です。Couplingを持つ量子ビット間で特定のゲート操作（例えばCNOTゲート）を適用することで、エンタングルメント状態を生成することができます。

  2. 複数の量子ビットに対する操作
    上記の制御NOTビットのように, 単一の量子ビットだけでなく、2つ以上の量子ビットに対する操作も必要です。これらの量子ビット間にはCouplingが存在する必要があります。

  3. 計算の正確性
    特定の量子アルゴリズムを実行するためには、特定の順序と組み合わせで量子ゲートを適用する必要があります。このため、量子ビット間の正確なCouplingが必要となります。

  4. フィジカルレベルでの接続
    実際の量子コンピュータのハードウェアにおいて、全ての量子ビットが直接的に他のすべての量子ビットとCouplingしているわけではありません。物理的に直接相互作用できる量子ビットのペアは限られています。この制約の中で効果的な計算を行うために、どの量子ビットがどの量子ビットと直接的にCouplingしているかを理解することは必要となります。

まだHW的な注意点はピンときませんが，頭に入れておきましょう！

Q14.3 選択肢解説

[A]は正しくパラメータを指定できており大正解です😋　一度パラメータを整理しましょう！

  • shots: 試行回数
  • backend: バックエンドを指定
  • coupling_map: 結合する量子ビット同士を指定
    色々なフォーマットが許されるので，qiskit documentで詳細を確認してみましょう。

[B]は get_backend()メソッドがGetBackendという異なるメソッド名で呼ばれているためerrorになるようです！なので，この選択肢は不正解です🙃
また，iterationを指定していると思われるloopというパラメータも，適切に実行されることを確認しました！

[C]も[B]と同じように，repeatというパラメータは取らないので不正解です🙃

[D]はQuantum Circuit インスタンスを第一因数に指定していないことでerrorとなります！
通常iteration回数はshotsというparameter名を指定するかと思いますが，shotでもOKなようです！
シミュレータでは特にエラーとなることなく，iterationが実行されるようです。

Q14.4 シミューレータ

特にありません！

Q14.5 Qiskit API

特にありません！

つぎは，全問と同様にCouplingについての問題です！

Q15

Which of these would execute a circuit on a set of qubits which are coupled in a custom way?

from qiskit import QuantumCircuit, execute, BasicAer  
backend = BasicAer.get_backend('qasm_simulator')
qc = QuantumCircuit(3)
    # insert code here

[A]
execute(qc, backend, shots=1024, coupling_map=[　[0,1], [1,2]　])

[B]
execute(qc, backend, shots=1024, custom_topology=[ [0,1],[2,3] ])

[C]
execute(qc, backend, shots=1024, device="qasm_simulator", mode="custom")

[D]
execute(qc, backend, mode="custom")

答え

[A]

Q15.1 用語

今回解説する用語は特にありません！

Q15.2 背景

Q14とほとんど同じため，今回開設すべきことはありません！

Q15.3 選択肢解説

いずれも実行してもエラーにはなりません！
なので，公式ドキュメントのexecuteメソッドの使い方から正解/不正解を判断したいと思います。

[A]は，公式ドキュメントに則った申し分ない使い方で正解と言えます😋

[B]は, custom_topologyという引数が使われています。
ただし，公式Document上にはこのparameterの存在は確認できませんでした。
この通りに実行しているのにエラーにならないのは謎ですが，ここでは不正解ということになるかと思います🙃

[C]は，[B]と同様にdevice, modeというparameterは存在しないため，不正解になっていると思われます🙃

Q15.4 シミューレータ

Q15.5 Qiskit API

つぎは，BasicAerクラスで実行できるシミュレータの種類に関する知識を問う問題です！

Q16

Which three simulators are available in BasicAer?

[A]
qasm_simulator

[B]
basic_qasm_simulator

[C]
statevector_simulator

[D]
unitary_simulator

[E]
quantum_simulator

[F]
quantum_circuit_simulator

答え

[A], [C], [D]

Q16.1 用語

今回は特別な用語はありません！

Q16.2 背景

Aer, BasicAerともにqiskitシミュレーションバックエンドを管理するためのクラスです。Aerの方が高性能なシミュレーションを提供します。BasicAerはAerの下位互換を提供するためのクラスで，より簡素なシミュレーション環境を提供します。

BasicAerは"qasm_simulator", "satevector_simulator", "unitary_simulator"の3種類を提供します！

ちなみに，Aerは12種類のシミュレーションを提供する。

Aer.backends()

で確認できるので，興味があれば試して確認してみましょう！

Q16.3 選択肢解説

この選択肢については，[A], [C], [D]のシミュレーション以外はBasicAer classでは提供されていないので不正解となります🙃

Q16.4 シミューレータ

今回はシミュレーションすることはありません！

Q16.5 Qiskit API

BasicAer

次は, backendをインスタンス化する際ののシミュレータの種類の指定の仕方を問う問題です。

Q17

Which line of code would assign a statevector simulator object to the variable backend ?

[A]
backend = BasicAer.StatevectorSimulatorPy()

[B]
backend = BasicAer.get_backend('statevector_simulator')

[C]
backend = BasicAer.StatevectorSimulatorPy().name()

[D]
backend = BasicAer.get_back('statevector_simulator')

答え

[B]

Q17.1 用語

今更ですがbackendとは，実際の量子デバイスやシミュレーションを表すオブジェクトです。バックエンドは、量子回路の実行やシミュレーションを担当し、結果を提供します。
ややこしいですが，AerやIBMQはバックエンドそのものではなく，プロバイダに当たります。それぞれのプロバイダが異なるバックエンドを管理しています。
総括すると、プロバイダはバックエンドを提供し、バックエンドは実際の量子デバイスやシミュレーションを表します。ユーザーはプロバイダを介してバックエンドを選択し、量子回路を実行したり、結果を取得したりすることができます！
backendは run, status, properties, configurationなどのメソッドを提供しています。

Q17.2 背景

BasicAerやqiskit.providers.basicaerが存在しお互い似ていて困りますね。。。。pythonの初学者への話になってしまいますが，ClassとModuleの違いを今一度はっきりさせましょう！まず基本的な名称のルールですが，pythonでは小文字は，関数や変数，モジュールをあわらし，単語文頭が大文字になっている場合はクラスです。また，モジュールは
関連する関数，クラス，変数などのコードの集合体です。そのため，今回のケースでは，BasicAerはクラスで，qiskit.providers.basicはモジュールを指します。

Q17.3 選択肢解説

暗記が苦手な私には酷な問題です笑

[A]の選択肢ですが，BasicAerはStatevectorSimulatorPy()のクラスは持っていません。ちなみに，StatevectorSimulatorPy()のインスタンスはqiskit.providers.basicaerモジュールに入っています。なので，

backend = qiskit.providers.basicaer.StatevectorSimulatorPy()
backend = BasicAer.get_backend("statevector_simulator")

上記は全く同じbackendを指定していることになります。
選択肢はqiskit.providers.basicaerモジュールから呼び出してないので不正解です🙃
当然，選択肢のように呼び出すとエラーになります！

[B]は正しいbackendインスタンスの作り方のため，正解となります😋

[C]は[A]と同じ理由で不正解です🙃

[D]はBasicAerのメソッドをget_backendではなく，get_backとなっているためエラーになり不正解になります🙃

Q17.4 シミューレータ

特になしです！

Q17.5 Qiskit API

StatevectorSimulatorPy
providers.basicaer

次は，マニュアルで演算子をインスタンス化する方法に関する問題です！

Q18

Which code fragment would yield an operator that represents a single-qubit X gate?

[A]
op = Operator.Xop(0)

[B]
op = Operator([[0,1]])

[C]
qc = QuantumCircuit(1)
qc.x(0)
op = Operator(qc)

[D]
op = Operator([[1,0,0,1]])

答え

[C]

Q18.1 用語

operatorとは，物理学で扱う演算子のことです。数学では作用素と言います。量子情報の分野では，量子ビットや古典ビットに対する何らかの操作を演算子で表現することが多いです。

Q18.2 背景

この問題は，qiskitのOperatorクラスに関する問題です。
このOperatorクラスを使って自分で定義したい演算子を作っておくと，再利用しやすくていいですね！

Q18.3 選択肢解説

Operator Classの最も簡単な使い方は，リストかNumpy Arrayで与えます。
[A]はOperatorオブジェクトはXop()のメソッドは持ちません。そのため，不正解です🙃
[B]はOperatorオブジェクトとしての使い方は間違っておらず，指定したオペレータオブジェクトを作成できます。しかし，2行1列のベクトルができるだけでNOTゲートはできません。そのため不正解です🙃
[C]は単一量子ビットを持ちX回路を挿入した量子回路を作成し，そのQuantumCircuitオブジェクトをOperatorのparamaterに入れています！OperatorクラスはQuantumCircuitオブジェクトをパラメータとして取ることができます！なので，NOT回路表すQuantumCircuitオブジェクトをパラメータに取りOperatorオブジェクトを作成しているため，題意を満たし正解となります😋
[D]は[B]と似ています。与えられた書き方でOperator演算子を作ることはできますが，NOTゲートにはなりません。なので，題意を満たさず不正解となります🙃

ちなみに，リストを与えてNOT Gateを作る場合，

op_x = Operator([[0,1],[1,0]])

のようにして作ることができます。
ちなみに，Operatorオブジェクトの使い方は，QuantumCircuitのappendメソッドに挿入して回路に追加することができます！

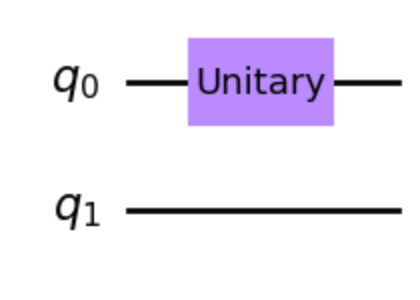
Q18.4 シミューレータ

今回は，自作したOperatorを使ってNOTゲートを試作して下記の回路を設計してみましょう！
この結果をシミュレートすると100%の確率で{01}が検出されることが確認できます！

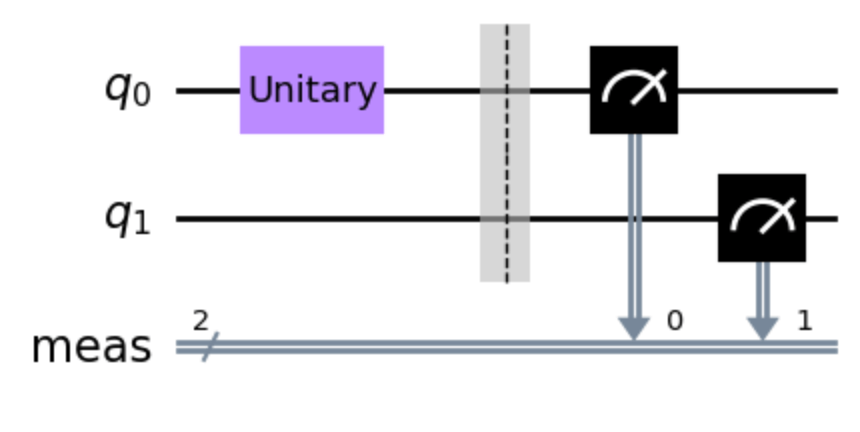
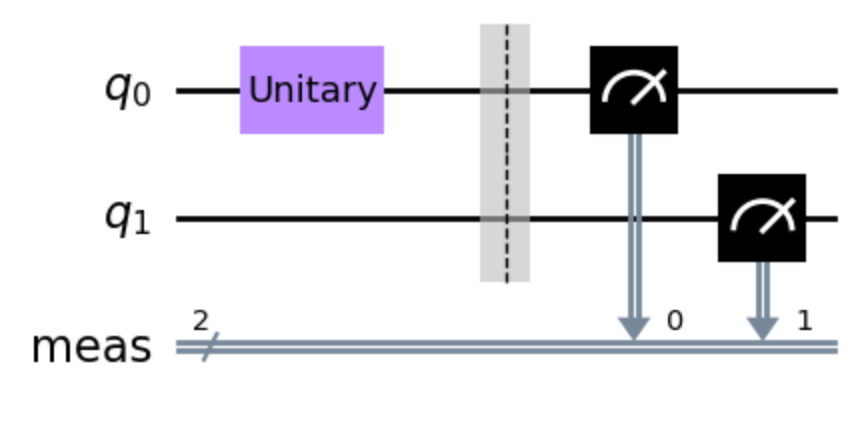
Q18.5 Qiskit

operator API

つぎは，量子フィデリティの考え方と意味の理解を問う問題です！

Q19

What would be the fidelity result(s) for these two operators, which differ only by global phase?

    op_a = Operator(XGate())
    op_b = numpy.exp(1j * 0.5) * Operator(XGate())

[A]
state_fidelity() of 1.0

[B]
state_fidelity() and average_gate_fidelity() of 1.0

[C]
average_gate_fidelity() and process_fidelity() of 1.0

[D]
state_fidelity()
average_gate_fidelity() and process_fidelity() of 1.0

答え

[C]

Q19.1 用語

まずfiderityについてです。まだ50%程度の理解だと思いますが，それでもすごく時間がかかりました。。。

  • state_fidelity(状態フィデリティ)
    ２つの量子状態間の類似度を評価します！

  • average_gate_fidelity(平均ゲートフィデリティ)
    実際の量子ゲート操作と理想的な量子ゲート操作間の類似度を評価するものです！

  • process_fidelity(プロセスフィデリティ)
    理想的な量子プロセス(量子回路の一連のゲート操作)と実際の量子プロセスの間の類似度を評価するために使用されます！

いずれも量子状態やプロセスの類似度を評価するためのツールという展で共通です！

Q19.2 背景

fiderityについて

上記でも簡単に述べていますが，fiderityとは, 2つの量子状態の「近さ」または「類似性」を評価するための指標です。2つの量子状態が純粋状態の場合は，絶対値の内積の二乗に等しいです。

\begin{align} F \left( \ket{\psi}, \ket{\phi}\right) = | \braket{\psi | \phi} |^2 \end{align}

混合状態の場合は，少し複雑となり2つの密度行列の\rho，\sigmaに対するfiderityは

\begin{align} F \left( \rho, \sigma \right) = \left( Tr(\sqrt{\sqrt{\rho} \sigma \sqrt{\rho}}\right)^2 \end{align}

となります。ちなみに，ここででてくる$ Tr $はトレースです。
内積の定義でもわかる通り，Fiderityは0から1の間の値を取り，両状態が完全に同じ場合Fiderityは1となり,0に近づくほど異なる度合いが大きくなります。

例えば，Fiderity=0.75とはどんな状態？

例を使って，Fiderityの値とその際のエラーの大きさをを天下り的に検証してみましょう。
まず，２状態を下記のように準備します。

\begin{align} \ket{\psi} &= \cos{\theta} \ket{0} + \sin{\theta} \ket{1} \\ \ket{\phi} &= \cos{( \theta + \delta \theta )} \ket{0} + \sin{( \theta + \delta \theta)} \ket{1} \\ \end{align}

\thetaはある状態の位相で \delta \thetaはエラーで生じる位相差です。
この2量子状態のFiderityは, 上記の内積の定義にしたがって計算すると

\begin{align} | \braket{\psi | \phi} | &= \cos{\theta} \cos{(\theta + \delta \theta)} + \sin{\theta} \sin{(\theta + \delta \theta)} \\ &= \cos{\left( (\theta) - (\theta + \delta \theta) \right)}\\ &= \cos{\delta \theta} \\ F \left( \ket{\psi}, \ket{\phi}\right) &= \cos^2{\delta \theta} \end{align}

つまり，Fiderityが0.75である場合，

\begin{align} F \left( \ket{\psi}, \ket{\phi}\right) &= \cos^2{\delta \theta} = 0.75=\frac{3}{4} \\ &\Leftrightarrow | \cos{\delta \theta} | = \frac{\sqrt{3}}{2}\\ \delta \theta &= \frac{\pi}{6}, - \frac{\pi}{6} \end{align}

この状態ベクトルの場合，エラーによって\frac{\pi}{6}程度の位相差が出てしまう場合，Fiderityが0.75程度になるということがわかりました！

エラーの影響について

上記の２状態のそれぞれに対して，ベル状態を作ろうとした時にどの程度の検出確率差が出るかを検証してみましょう。具体的には，上記の例で,\theta = \frac{\pi}{4}, \delta \theta = \frac{\pi}{6}を当てはめるとシミュレーションすることができます。これまで学んできた通り，理想的なBell状態\ket{\Phi^{+}} (\theta = \frac{\pi}{4}, \delta \theta=0)は

\begin{align} \ket{\Phi^{+}} &= \cos{(\frac{\pi}{4})} \ket{00}+ \sin{(\frac{\pi}{4})} \ket{11}\\ &= \frac{1}{\sqrt{2}} \left( \ket{00} + \ket{11} \right) \end{align}

であり, 理想的にはそれぞれ50%, 50%の検出確率で\ket{00}, \ket{11}が観測されます。

では，Fiderity0.75の場合 (\theta = \frac{\pi}{4}, \delta \theta=\frac{\pi}{6})どうなるでしょうか？

\begin{align} \ket{\Phi'^{+}} &= \cos{(\frac{\pi}{4}+\frac{\pi}{6})} \ket{00}+ \sin{(\frac{\pi}{4}+\frac{\pi}{6})} \ket{11}\\ &= \cos{(\frac{5 \pi}{12})} \ket{00}+ \sin{(\frac{5 \pi}{12})} \ket{11} \end{align}

\frac{\pi}{3} < \theta = \frac{5 \pi}{12} < \frac{\pi}{2}のため，

\begin{align} 0 < \cos^2{\theta} = \frac{5 \pi}{12} < \frac{1}{4} \\ \frac{3}{4} < \sin^2{\theta} = \frac{5 \pi}{12} < 1 \\ \end{align}

つまり，\ket{00}が測定される確率は\frac{1}{4}以下，\ket{11}は\frac{3}{4}以上となり，50%50%で観測される理想状態から大きく外れることがわかります！エラー訂正の必要性もなんとなくわかりましたね！

Q19.3 選択肢解説

今回取り扱うのは2つのOperatorオブジェクトの忠実度を計算する問いです！
Operatorオブジェクトはゲート操作を表すため，忠実度は
average_gate_fidelityとprocess_fidelityを使って計算できます！

一方で，Inputがquantum stateでない場合はqiskit errorになってしまいます！

なので，state_fidelityでは忠実度は計算できません。なので，state_fidelityが入っていない選択肢が正解となります！
なので，正解は[C]となります！

Q19.4 シミューレータ

今回はシミュレーションすることはないためskipします。

Q19.5 Qiskit API

XGate

average_gate_fidelity

process_fidelity

state_fidelity

quantum channelとは量子ビットの状態を操作したり伝達したりするための数学的な表現です

\rho_{out}= \epsilon (\rho_{in})
\rho_{in}は入力の密度行列，\rho_{out}は出力の行列を表す。
\epsilonは量子チャネルを表すリニアな写像です。

状態の密度行列を別の密度行列に変換するリニアな写像で，行列演算に相当します。

量子チャネルは，様々な操作や物理的なプロセスをモデル化するために使用されます。
例えば，ユニたり変換や測定，ノイズやエラーの効果を表現するために使用されます！
量子チャネルの理解と分析は，量子情報処理や量子通信などの応用で重要な役割を果たします！

Q20

Given this code fragment, which output fits most closely with the measurement probability distribution?

qc = QuantumCircuit(2, 2)
qc.x(0)
qc.measure([0,1], [0,1])
simulator = Aer.get_backend('qasm_simulator')
result = execute(qc, simulator, shots=1000).result()
counts = result.get_counts(qc)
print(counts)

[A]
{'00': 1000}

[B]
{'01': 1000}

[C]
{'10': 1000}

[D]
{'11': 1000}

答え

[B]

Q20.1 用語

今回はこれまでの問題の復習のような問題のため，新しい用語は出てきていません！

Q20.2 背景

今まで解いてきた問題の総集編のような問題ですね！
今まで19問解いてきているのであれば，この問題は簡単ですね！

Q20.3 選択肢解説

量子ビット２個，古典ビット２個を準備して0番目の量子ビットにNOT Gateをかけます．
そして，準備した古典ビットで２つの量子ビットをそれぞれ測定しています．

初期状態は

\begin{align} \ket{\Psi} &= \ket{q_{0}} \ket{q_{1}} \\ &= \ket{0}_{q_{1}} \ket{0}_{q_{0}} \\ &= \ket{00} \\ \ket{\Psi '} &= \hat{X_{q_{0}}} \ket{\Psi} \\ &= ( \ket{0}\bra{1} + \ket{1}\bra{0})_{q_{0}} \ket{0}_{q_{1}} \ket{0}_{q_{0}} \\ &= \ket{0}_{q_{1}} \ket{1}_{q_{0}} \\ &= \ket{01} \end{align}

得られる結果は\ket{01}となるため，それ以外の選択肢は不正解です🙃
唯一の正解は[B]となります😋

Q20.4 シミューレータ

今回はシミュレーションはありません！

Q20.5 Qiskit API

APIもこれまで使ったもの以外はありまえん！

後半のまとめ

最後は総復習のような問題のため，さっぱり終わってしまいました！
さて，後半は

  • 量子回路内の便利機能
  • qasm simulatorの使い方
    が主でした。
    何気にFiderityの計算も出てきたので，実際の数値を使って量子状態の類似性についても議論してみました。
    お付き合い誠にありがとうございました！

今後も量子コンピュータの基礎技術やその実装，サービス展開などの記事を書いていきたいと思います！
また，今回は各設問に関して背景知識などを加えましたが，重要な事項ごとに記事化して体型的に学べるようにしたいと思います！何より自分の知識定着, 実装力強化のために今後も執筆活動を続けていきたいと思います！

受験時の注意点

今回の試験の合格体験記については別記事になりますので，よろしければお越しください！
特に，受験時にいくつもトラブルが発生しました。。。本試験はピアソンVUEという団体が提供するオンライン試験サービスを利用することになりますが，オンラインで自宅でも受験できるサービスで大変魅力です。しかし, 受験前に2度試験が中断する(そもそも開始できない)というハプニングが発生し，休みの一部を無駄にしてしまって，大変残念な気持ちになりました。その辺りの苦労話も含め，合格体験記に載せたいと思います！

Discussion