UKIさんのシストレのすすめを正座して読んで手を動かしてみる #3
きっかけ
UKIさんのシストレのすすめを正座して読んで手を動かしてみる #2の続きです。読んで手を動かして学んでいきましょう!
この章は本来は株式や債券、為替、商品先物、仮想通貨などなどいろいろなアセットクラスの特徴を理解してからどこでトレードをするか決めようね、という話なのですが、便宜上Binanceの永久先物を対象に記事の内容をフォローしていきます。
第六回 トレードする市場を選定する
2. 市場の性質を定量化する
市場の性質を把握するためには、サンプルに対する基本統計量を分析します。
(中略)
ここで4つの基本統計量の意味は、以下の通りです。
1次モーメント:いわゆる平均値です。分布の中心傾向を示す尺度となります。健全な株式相場は右肩上がりに成長しているため、若干プラスの値となります。どちらかへ偏っていた場合、そちら側のトレードが有利となります。
2次モーメント:いわゆる標準偏差です。2次モーメントは1次モーメント周りの分布のバラツキを示します。東証1部などは小さく、新興市場は大きくなります。収益のばらつきに影響します。
3次モーメント:歪度と呼びます。3次モーメントは1次モーメントに対する左右の対称度を示します。歪度が正の場合、 「急に上がり、ダラダラ下げるような値動き」 が多いことを意味します。歪度が負の場合はその逆となります。即ち、 「コツコツ上昇した後、急落するような値動き」 が多いことを意味します。歪度とトレードスタイルとの関係は非常に重要となります。 一般的にポジティブスキューはトレンドフォロー寄り、ネガティブスキューはカウンタートレンド寄りの相場と言われます。
4次モーメント:尖度と呼びます。4次モーメントはリターンの分布が正規分布に対してどれだけ尖っているかを示します。尖度が正であれば中心が尖り裾野が長くなるファットテールな分布となります。尖度が負であれば中心が丸く裾野も短い分布全体がまとまった形状となります。 尖度はトレンドとレンジの比率を示し、フィナンシャルデータの分布の殆どは正となります。 これは「市場の値動きの8割は2割の期間で発生する」という格言を示しています。
基本統計量を確認するだけでもどのようなストラテジーが有望そうであるか、当たりを付けることができます。
実験
例によってBinance永久先物の主要な10銘柄を対象にやってみます。
期間は2022年10月15日からさかのぼって120日間の15分足、1時間足、4時間あし、日足を対象に、平均、標準偏差、歪度、尤度の4つの統計量を出して表にしてみます。
実験に利用したコードの抜粋はこちらです
# df_priceには例によって全銘柄の時間足が入れてあります
def get_effective_quantile(dataset, value):
return sum(dataset <= value) / len(dataset)
def render_market_statistics():
_target_symbols = ['BTCUSDT', 'ETHUSDT', 'BNBUSDT', 'XRPUSDT', 'ADAUSDT', 'SOLUSDT', 'DOGEUSDT', 'DOTUSDT', '1000SHIBUSDT', 'MATICUSDT']
_num_target_symbols = len(_target_symbols)
_target_time_units = ['15m', '1h', '4h', '1d']
_num_target_time_units = len(_target_time_units)
_df_statistics = pd.DataFrame()
_level_c_botter_requirements = [(0.000003424658, 0.000427373843), (0.000013698630, 0.000854747686), (0.000054794521, 0.001709495373), (0.000328767123, 0.004187391381)]
#_level_c_botter_requirements = [(0.000003424658, 0.000427373843 * 10), (0.000013698630, 0.000854747686 * 10), (0.000054794521, 0.001709495373 * 10), (0.000328767123, 0.004187391381 * 10)]
# 描画用のfigureとsubplotを用意 (メモリリークを防ぐためにplt.FigureとFigure.subplotsを使う)
_rows = _num_target_symbols
_cols = _num_target_time_units
#_fig = plt.Figure(figsize = (8 * _cols, 6 * _rows))
#_axs = _fig.subplots(_rows, _cols, squeeze = False)
_fig, _axs = plt.subplots(nrows = _rows, ncols = _cols, figsize = (8 * _cols, 6 * _rows))
_now = datetime.now(timezone.utc)
for _idx_symbol, _symbol in tqdm(enumerate(_target_symbols), total = _num_target_symbols):
for _idx_time_unit, _time_unit in enumerate(_target_time_units):
_df_price = df_price[_time_unit]
_df_price_symbol = _df_price.loc[_df_price['symbol'] == _symbol, :]
_series_close = _df_price_symbol.loc[_df_price_symbol.index > _df_price_symbol.index[-1] - timedelta(days = 120), 'close'].astype(float)
_series_logreturn = np.log(_series_close).diff()
# 対数リターンのヒストグラムを描画
_ax = _axs[_idx_symbol, _idx_time_unit]
_ax.hist(_series_logreturn, bins = 50, density = True)
_ax.grid()
_ax.set_title(f'対数リターンの分布 ({_symbol}, {_time_unit})')
_ax.set_xlabel('対数リターン')
_ax.text(0.99, 0.8, f'平均 = {_series_logreturn.mean():.05f}\n標準偏差 = {_series_logreturn.std():.05f}\n歪度 = {_series_logreturn.skew():.05f}\n尖度 = {_series_logreturn.kurt():.05f}', va='top', ha='right', size = 'medium', transform = _ax.transAxes)
# C級Botterになるための目標の正規分布を描画
_linspacex = np.linspace(_series_logreturn.min(), _series_logreturn.max(), 1000)
_ax.plot(_linspacex, norm.pdf(_linspacex, _level_c_botter_requirements[_idx_time_unit][0], _level_c_botter_requirements[_idx_time_unit][1]), label = 'C級Botter分布')
_ax.legend()
# 表として表示する統計量を記録しておく
_abs_mean = np.abs(_series_logreturn).mean()
_df_statistics = _df_statistics.append({
'シンボル': _symbol,
'時間足': _time_unit,
'平均': _series_logreturn.mean(),
'標準偏差': _series_logreturn.std(),
'歪度': _series_logreturn.skew(),
'尖度': _series_logreturn.kurt(),
'絶対値の平均': _abs_mean,
'0.01%リターンのために必要な予測精度': (_abs_mean + 0.08 * 0.01 + 0.01 * 0.01) / (2 * _abs_mean)}, ignore_index = True)
_fig.set_tight_layout(True)
_fig.savefig(f'binance_market_view.png', transparent = False)
_fig.show()
return _df_statistics
df_statistics = render_market_statistics()
統計量を計算した結果
結果はこのようになりました。
| シンボル | 時間足 | 平均 | 標準偏差 | 歪度 | 尖度 | 絶対値の平均 | 0.01%リターンのために必要な予測精度 | |
|---|---|---|---|---|---|---|---|---|
| 39 | MATICUSDT | 1d | 0.0069 | 0.0570 | 1.0087 | 3.2276 | 0.0414 | 0.5109 |
| 23 | SOLUSDT | 1d | -0.0007 | 0.0465 | 0.0189 | 0.3362 | 0.0364 | 0.5124 |
| 35 | 1000SHIBUSDT | 1d | 0.0024 | 0.0548 | 1.9247 | 10.2252 | 0.0347 | 0.5130 |
| 7 | ETHUSDT | 1d | 0.0021 | 0.0469 | 0.2384 | 1.8157 | 0.0332 | 0.5136 |
| 31 | DOTUSDT | 1d | -0.0013 | 0.0399 | 0.1440 | 0.5303 | 0.0305 | 0.5147 |
| 27 | DOGEUSDT | 1d | 0.0009 | 0.0414 | 0.2651 | 1.3941 | 0.0296 | 0.5152 |
| 15 | XRPUSDT | 1d | 0.0038 | 0.0399 | 1.1106 | 5.5549 | 0.0279 | 0.5161 |
| 19 | ADAUSDT | 1d | -0.0019 | 0.0356 | -0.2771 | 1.0673 | 0.0271 | 0.5166 |
| 11 | BNBUSDT | 1d | 0.0026 | 0.0294 | 0.3296 | 0.8766 | 0.0212 | 0.5213 |
| 3 | BTCUSDT | 1d | 0.0000 | 0.0300 | -0.0009 | 3.0688 | 0.0206 | 0.5219 |
| 38 | MATICUSDT | 4h | 0.0010 | 0.0238 | 0.5204 | 3.5734 | 0.0163 | 0.5276 |
| 22 | SOLUSDT | 4h | -0.0001 | 0.0221 | 0.4142 | 4.6250 | 0.0155 | 0.5290 |
| 34 | 1000SHIBUSDT | 4h | 0.0003 | 0.0211 | 1.0173 | 7.5885 | 0.0138 | 0.5326 |
| 6 | ETHUSDT | 4h | 0.0002 | 0.0193 | 0.1921 | 3.5193 | 0.0132 | 0.5341 |
| 30 | DOTUSDT | 4h | -0.0003 | 0.0179 | -0.0763 | 3.6741 | 0.0125 | 0.5359 |
| 14 | XRPUSDT | 4h | 0.0005 | 0.0185 | 1.0357 | 7.9933 | 0.0123 | 0.5367 |
| 26 | DOGEUSDT | 4h | 0.0000 | 0.0169 | -0.0348 | 2.6852 | 0.0119 | 0.5377 |
| 18 | ADAUSDT | 4h | -0.0004 | 0.0161 | 0.0053 | 2.4989 | 0.0115 | 0.5390 |
| 10 | BNBUSDT | 4h | 0.0003 | 0.0132 | 0.0777 | 3.0251 | 0.0094 | 0.5477 |
| 2 | BTCUSDT | 4h | -0.0001 | 0.0136 | 0.0447 | 5.0174 | 0.0091 | 0.5497 |
| 37 | MATICUSDT | 1h | 0.0002 | 0.0115 | 0.4237 | 7.9349 | 0.0077 | 0.5583 |
| 21 | SOLUSDT | 1h | -0.0000 | 0.0108 | 0.2843 | 6.1028 | 0.0074 | 0.5611 |
| 33 | 1000SHIBUSDT | 1h | 0.0001 | 0.0109 | 1.2144 | 13.7834 | 0.0070 | 0.5645 |
| 5 | ETHUSDT | 1h | 0.0001 | 0.0095 | 0.3172 | 7.8454 | 0.0063 | 0.5712 |
| 29 | DOTUSDT | 1h | -0.0001 | 0.0091 | -0.3189 | 6.3410 | 0.0062 | 0.5723 |
| 25 | DOGEUSDT | 1h | 0.0000 | 0.0093 | 0.5506 | 9.5877 | 0.0062 | 0.5729 |
| 13 | XRPUSDT | 1h | 0.0001 | 0.0091 | 0.6402 | 10.1502 | 0.0060 | 0.5751 |
| 17 | ADAUSDT | 1h | -0.0001 | 0.0083 | -0.1142 | 4.9261 | 0.0059 | 0.5768 |
| 9 | BNBUSDT | 1h | 0.0001 | 0.0068 | -0.1271 | 5.6331 | 0.0047 | 0.5951 |
| 1 | BTCUSDT | 1h | -0.0000 | 0.0069 | 0.0467 | 9.1299 | 0.0044 | 0.6013 |
| 36 | MATICUSDT | 15m | 0.0001 | 0.0059 | 0.1362 | 11.0283 | 0.0040 | 0.6136 |
| 20 | SOLUSDT | 15m | -0.0000 | 0.0055 | -0.2640 | 8.9781 | 0.0038 | 0.6183 |
| 32 | 1000SHIBUSDT | 15m | 0.0000 | 0.0057 | -0.1273 | 24.6020 | 0.0036 | 0.6235 |
| 28 | DOTUSDT | 15m | -0.0000 | 0.0047 | -0.6923 | 10.8869 | 0.0032 | 0.6387 |
| 24 | DOGEUSDT | 15m | 0.0000 | 0.0049 | 0.3031 | 17.1035 | 0.0032 | 0.6408 |
| 4 | ETHUSDT | 15m | 0.0000 | 0.0049 | 0.0814 | 23.5744 | 0.0032 | 0.6412 |
| 12 | XRPUSDT | 15m | 0.0000 | 0.0046 | 0.7375 | 22.1592 | 0.0031 | 0.6468 |
| 16 | ADAUSDT | 15m | -0.0000 | 0.0044 | -0.5650 | 10.7707 | 0.0030 | 0.6499 |
| 8 | BNBUSDT | 15m | 0.0000 | 0.0035 | -0.3815 | 10.7021 | 0.0024 | 0.6857 |
| 0 | BTCUSDT | 15m | -0.0000 | 0.0035 | -0.4847 | 26.4917 | 0.0022 | 0.7030 |
例えば、MATICUSDTの日足からはこんなことがわかりそうです。
- 価格上昇が一気に起こってだらだら下がりやすいらしい (歪度が正)
- 価格変動の大きいトレンドが短期間だけ起こる傾向があるらしい (尖度が正)
- 日足1本あたりの標準偏差が他の銘柄に比べて大きく、手数料負けしにくい
また、全体を見るとこんなことも想像できます
- 利益の出しやすさを考えると、日足や8時間足あたりから手を付けるのがよいのかも
- 歪度が比較的大きい銘柄があります。価格上昇と下降のスピードが異なるので、指値型Botを作るのであれば、上下の指値幅を変えられるような仕組みを準備しておいた方がよさそうです。成行型Botならば売買シグナルは上昇中と下降中では非対称にする仕組みがあるとよさそうです
このような「予習」をある程度した上でどこで取引をするのか、どんな取引をするのかイメージを膨らませると、見通しがだいぶ良くなることがわかりました。
歪度と尖度と、累積対数リターンの形の関係を見てみる
これだけではイマイチ実感がつかめないので、歪度と尖度について、日足の累積対数リターンと見比べて様子を見てみます。
まずは歪度から見てみます。
歪度がもっとも大きいのは1000SHIBUSDTの1.9247です。グラフは以下のような形です。UKIさんの記事通り、ダラダラ下がって…ドガッと 上がる 感じになっていますね。他の銘柄と比べてy軸の範囲が広いことにも注意です。

歪度が最も0に近いのは、BTCUSDTの-0.0009です。さすがの最大時価総額銘柄…! グラフは以下のような形です。ドガッとあがるしドガッと下がります、どっちかがゆるゆるしてることはありません、と言う感じでしょうか。

歪度が最も小さいのは、ADAUSDTの-0.2771です。グラフは以下のような形です。1000SHIBほどではないですが、ダラダラ上がって…ドガッと 下がる パターンになっています。

また、改めて表の値を見てみると、ここ3カ月のBinanceでは、歪度は正の値を取っている銘柄と時間足がとても多いことがわかります。
続けて尖度についてみてみます。
尖度がもっとも大きいのはまたしても1000SHIBUSDTの10.2252です。グラフは以下のような形です。UKIさんの記事通り、激しく上下して価格が変化していく様子がわかります。

尖度が最も小さいのはSOLUSDTの0.3362です。グラフは以下のような形です。鋭く上下しているように見えますが、y軸の数字に注目すると、1000SHIBと比較すると上下の変動幅が半分くらいになっていることがわかります。

なんとなく歪度と尖度についてイメージができてきました。
4.ストラテジーの要件と市場の性質を照合する
以下、市場の選定が重要であることを説明します。システムトレードとは、「母集団の持つ分布(ここでは市場分布と呼ぶことにします)に対して投資指標を用いて新たに分布(トレード分布と呼ぶことにします)を再抽出すること」です。当然ながらどのような投資指標を使っても元々の母集団の分布を変化させるということはできません。従って元々の市場分布から逸脱するようなトレード分布を得ることはできません。 ストラテジーの検討を始める前に、所望の期待成長率E、標準偏差σ、トレード数Nについて、対象市場が適合しているか調査を行うべきです。
以下に、ある市場分布に対して期待値1.0%、標準偏差5.0%(SR=0.2)の目標分布、期待値0.5%、標準偏差2.5%(SR=0.2)のトレード分布を書き込んだ図を示します。これを見ると前者はどう考えても実現性はなく、市場選定の時点で間違っていることに気付くでしょう。
実験
まず、今回は時間足が何種類かあるので、その時間足ごとに必要な
実験に利用したコードの抜粋はこちらです
# 所望の年率リターン
_ret = 0.12
# 所望の最大ドローダウン率
_drawdown = 0.12
# トレード間隔
_trade_interval_targets = [0.25, 1, 4, 24]
df_statistics = pd.DataFrame()
for _trade_interval in _trade_interval_targets:
# 1年間のトレード回数N
_N = 365 * 24 / _trade_interval
# 一回のトレードの利益の期待値e
_e = _ret / _N
# 一回のトレードの標準偏差
_sigma = 2 / 3 * np.sqrt(_drawdown * _e)
# シャープレシオ
_SR = _e / _sigma
df_statistics = df_statistics.append({
'トレード間隔 (時間)': _trade_interval,
'1年間のトレード回数N': _N,
'1回のトレードの利益の期待値e': _e,
'1回のトレードの利益の標準偏差': _sigma,
'シャープレシオ': _SR}, ignore_index = True)
print(df_statistics.to_markdown(floatfmt = ['.0f', '.2f', '.0f', '.12f', '.12f', '12f'], tablefmt = 'github'))
結果は以下のようになりました。
| トレード間隔 (時間) | 1年間のトレード回数N | 1回のトレードの利益の期待値e | 1回のトレードの利益の標準偏差 | シャープレシオ |
|---|---|---|---|---|
| 0.25 | 35040 | 0.000003424658 | 0.000427373843 | 0.008013 |
| 1.00 | 8760 | 0.000013698630 | 0.000854747686 | 0.016027 |
| 4.00 | 2190 | 0.000054794521 | 0.001709495373 | 0.032053 |
| 24.00 | 365 | 0.000328767123 | 0.004187391381 | 0.078514 |
では早速このパラメータで描画してみましょう。
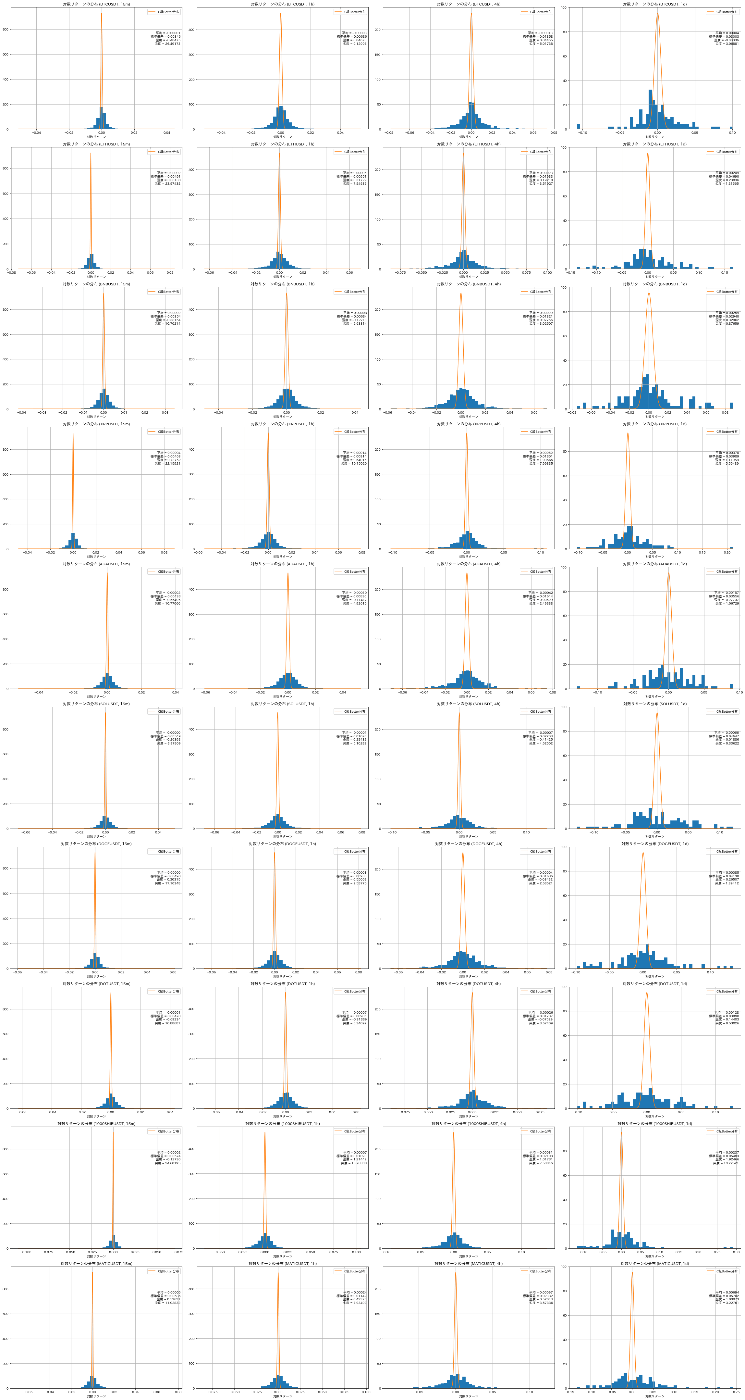
あれ? オレンジで描画したC級Botterになるために必要な分布が、ブルーの実際の対数リターンの分布をはるかに超えてしまいました。これではC級Botterは絵にかいた餅です。
C級Botterになるための分布がマーケットのリターンの分布に入らないのはなぜ?
C級Botterになるための分布の標準偏差が小さすぎる
今回描画してみたC級Botterになるために必要なパラメータは、標準偏差
仮想通貨のマーケットでは、もう少し大きい標準偏差を受け入れなければいけないのかもしれません。
全ての時間足でトレードする前提でトレード戦略に必要な期待値と標準偏差を求めたから?
全ての時間足でトレードすると仮定して所望の期待値、標準偏差を持つトレード戦略のリターン分布のヒストグラムを書くと、そのヒストグラムの面積は元のマーケットのリターン分布のヒストグラムと同じになります。(何しろ積み上げる対象の時間足の本数が同じなので) この同じ面積を持つ二つのヒストグラムを比べると…一致するかしないかの二択になってしまうでしょう。
UKIさんの図のように、マーケットそのもののリターン分布のヒストグラムの中に所望のトレード戦略のリターン分布がまるっと含まれるようになるには、時間足ごとに毎回トレードしないようにして、トレード戦略のヒストグラムの面積をぐっと小さくしなければいけない気がしました。
例えばトレード回数を半分にすれば、ヒストグラムの面積は半分になるはずです。
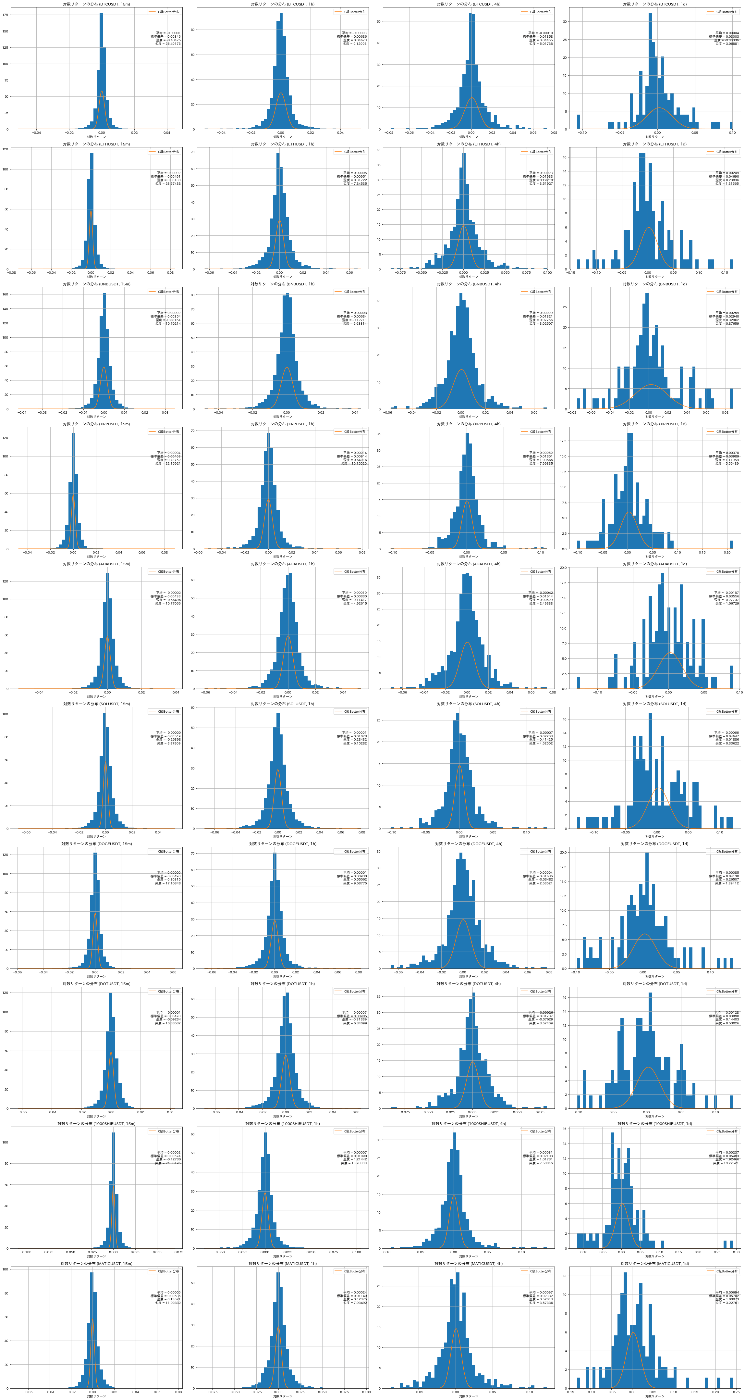
もう一回実験してみよう
試しに、以下のような条件を加えて改めて必要な期待値と標準偏差を計算しなおしてみました。
- トレード回数を全ての時間足でするのではなく、平均で4本に1回取引するようにする
- 許容ドローダウンを24%にする
結果は以下のようなものになりました。
| トレード間隔 (時間) | 1年間のトレード回数N | 1回のトレードの利益の期待値 | 1回のトレードの利益の標準偏差 | シャープレシオ | |
|---|---|---|---|---|---|
| 0 | 0.25 | 4380 | 0.000027397260 | 0.002093695690 | 0.013086 |
| 1 | 1.00 | 1095 | 0.000109589041 | 0.004187391381 | 0.026171 |
| 2 | 4.00 | 274 | 0.000438356164 | 0.008374782761 | 0.052342 |
| 3 | 24.00 | 46 | 0.002630136986 | 0.020513944472 | 0.128212 |
この期待値と標準偏差をもとに、改めてトレード戦略のヒストグラムをマーケットのヒストグラムと重ねて描画したところ、UKIさんの記事のようなそれっぽい見え方になりました。
よかったよかった。
おわりに
ストラテジーを考える前に、トレードをして実現したい期待値と標準偏差が現実的かどうかをあらかじめ調べておくと、無茶振りなのかそうでないのかが推測できることが手を動かして理解できました。
これから「これくらい利益が欲しいな」と考えるとき、「ちょっと待て」と立ち止まって考えるようにしようと思います。慣れてくると考えなくてもできるようになりそうな気もします。
おまけ
ヒストグラムの重ね合わせをしているときふと思ったのですが、なんかトレードってマーケットから出てくるリターンの積み木を、レバレッジ・ロング・ショートで別の場所に移動させる遊びなんだなと思いました。
流動性が許す限り、レバレッジとロングとショートを使って積み木をヒストグラム上の好きな場所に移動して置くことができるイメージです。流動性がない場合は積み木はどこにも積むことができません。
あと、UKIさんの記事にあった、歪度がポジティブスキューだとトレンドフォロー寄り、ネガティブスキューだとカウンタートレンド寄り、という話は今一つ分かっていません。ポジティブスキューなら上昇に順張りしやすく、ネガティブスキューなら下落に順張りしやすい、とかならまだわかるのですが。
カウンタートレンドというのは、戻り売りのことなんですかね?

Discussion