rodisを用いたバイナリ格子のRCWA解析(2)
rodisでバイナリ格子のRCWA解析を試す。
はじめに
前回rodisを用いた、RCWA解析の結果を紹介しましたがRodisを用いたバイナリ格子のRCWA解析、そのなかのある条件では、計算が収束せず、グラフに表示されませんでした。
この記事では、rodisの改修を行い、Moharamの論文の条件での、収束した解析結果を紹介します。
rodisのインストール
rodisのインストールは、前回の記事Rodisを用いたバイナリ格子のRCWA解析で紹介しましたのでそちらをご覧ください。
rodis ソースコードの改修
前回は、ソースコードの改変なしで、環境設定のみubuntu-22.04に合わせて、RCWA解析を実行しました。ただ、4つある条件のうち、3番目と4番目のConicalでの結果が、収束せず、グラフにはTEとTMしか表示されない状態になりました。解析の結果2次の偏微分方程式(参考文献の例えば式(15))に対応する右辺の行列の固有値を求めた後、その固有値の正の平方根を用いてそのあとの解を表現しているので、ubuntu-22.04の環境で、そうなるように調整します。具体的には、固有値、固有ベクトルを求める関数、CompleEigenの直後で、以下のように、元のコードをコメントアウトして、
W1=ComplEigen(W1,L1);
W2=ComplEigen(W2,L2);
for(i=0;i<n;i++)
{
// L1(i,0)=sqrt(L1(i,0));
// if(real(L1(i,0))<-1e-8) L1(i,0)=-L1(i,0);
// L2(i,0)=sqrt(L2(i,0));
// if(real(L2(i,0))<-1e-8) L2(i,0)=-L2(i,0);
if (sqrt(L1(i,0)).imag() < 0.0)
L1(i,0)=conj(sqrt(L1(i,0)));
else
L1(i,0)=sqrt(L1(i,0));
if (sqrt(L2(i,0)).imag() < 0.0)
L2(i,0)=conj(sqrt(L2(i,0)));
else
L2(i,0)=sqrt(L2(i,0));
のように、変更しています。
TE,TMも同様に変更して、変化しないことを確認します。
W=ComplEigen(W,L);
for(i=0;i<n;i++)
{
// L(i,0)=sqrt(L(i,0));
// if(real(L(i,0))<0) L(i,0)=-L(i,0);
if (sqrt(L(i,0)).imag() < 0.0)
L(i,0)=conj(sqrt(L(i,0)));
else
L(i,0)=sqrt(L(i,0));
}
W=ComplEigen(W,L);
for(i=0;i<n;i++)
{
// L(i,0)=sqrt(L(i,0));
// if(real(L(i,0))<0) L(i,0)=-L(i,0);
if (sqrt(L(i,0)).imag() < 0.0)
L(i,0)=conj(sqrt(L(i,0)));
else
L(i,0)=sqrt(L(i,0));
}
バイナリ格子のRCWA解析
実行するためのpython入力ファイルrodis_01lambda_05depth.pyは以下の通りです。
実行スクリプト(test01.py)
#!/usr/bin/env python
# coding: utf-8
# Reproduces Fig. 2 in Moharam, Grann, Pommet, and Gaylord, "Formulation for stable and
# efficient implementation of the rigorous coupled-wave analysis of binary gratings",
# J. Opt. Soc. Am. A 12(5), pp. 1068–1076, 1995 (doi:10.1364/JOSAA.12.001068)
import rodis
from math import pi
import numpy
import matplotlib.pyplot as plt
def moharam(theta_rad,phi_rad,psi_rad,wavelength,ambient,pitch,fillfactor,thicknesses,substrate,norders):
# rodis data
rodis.set_lambda(wavelength) # wavelength
rodis.set_N(norders) # orders of diffraction
rodis.set_alpha(theta_rad) # angle of incidence
rodis.set_delta(phi_rad) # 0 for planar diffraction
rodis.set_psi(psi_rad) # polarization angle
solutions = []
width = fillfactor*pitch
for d in thicknesses:
binary = rodis.Slab( ambient(0.5*width) + substrate(width) + ambient(0.5*width) )
incident = rodis.Slab( ambient(pitch) )
transmission = rodis.Slab( substrate(pitch) )
grating = rodis.Stack( incident(1.) + binary(d) + transmission(1.) )
grating.calc()
solutions.append(grating.diffr_eff().T(1))
return solutions
def plot(depths,wavelength,multiplier,TEsolutions,TMsolutions,conicalsolutions):
plt.plot(depths/wavelength, TEsolutions, 'b.-', \
depths/wavelength, TMsolutions, 'r.-', \
depths/wavelength, conicalsolutions, 'k.-', \
)
plt.xlabel('Normalized groove depth $d/\lambda$')
plt.ylabel('Diffraction efficiency $DE_1$')
plt.legend(('TE', 'TM', 'conical $(\\phi = 30^\circ, \psi = 45^\circ)$'))
plt.axis('tight')
plt.ylim([0,1])
if multiplier == 1:
plt.title("First-order transmitted diffraction efficiency\n" + \
"$n_I = 1$, $n_{II} = 2.04$, $\\theta = 10^\circ$, $\\Lambda = \lambda_0$")
plt.savefig("moharam1995_lambda_" + str(int(depths[-1]/wavelength)) + "lambda.png")
plt.savefig("moharam1995_lambda_" + str(int(depths[-1]/wavelength)) + "lambda.svg")
else:
plt.title("First-order transmitted diffraction efficiency\n" + \
"$n_I = 1$, $n_{II} = 2.04$, $\\theta = 10^\circ$, $\\Lambda =$ " + \
str(multiplier) + "$\lambda_0$")
plt.savefig("moharam1995_"+str(multiplier)+"lambda_" + str(int(depths[-1]/wavelength)) + "lambda.png")
plt.savefig("moharam1995_"+str(multiplier)+"lambda_" + str(int(depths[-1]/wavelength)) + "lambda.svg")
plt.show()
def main():
wavelength = 1.55
norders = 15
theta = 10.*pi/180 # angle of incidence
phi = 30.*pi/180 # 0 for planar diffraction
psi = 45.*pi/180 # polarization angle
ambient = rodis.Material(1.0)
substrate = rodis.Material(2.04)
multiplier = 1
pitch = multiplier*wavelength
fill = 0.5
depths = numpy.linspace(0.,5.,100)*wavelength
# TE (psi = pi/2)
print("TE")
TEsolutions = moharam(theta,0.,pi/2,wavelength,ambient,pitch,fill,depths,substrate,norders)
# TM (psi = 0)
print("TM")
TMsolutions = moharam(theta,0.,0.,wavelength,ambient,pitch,fill,depths,substrate,norders)
# Conical
print("Conical: \t phi = %.1f \t psi = %.1f" % (phi*180/pi,psi*180/pi))
conicalsolutions = moharam(theta,phi,psi,wavelength,ambient,pitch,fill,depths,substrate,norders)
plot(depths,wavelength,multiplier,TEsolutions,TMsolutions,conicalsolutions)
if __name__ == "__main__":
main()
実行するには以下のようにします。
python3 test01.py
test01.py の実行結果
test01.py の実行結果を以下に示します。
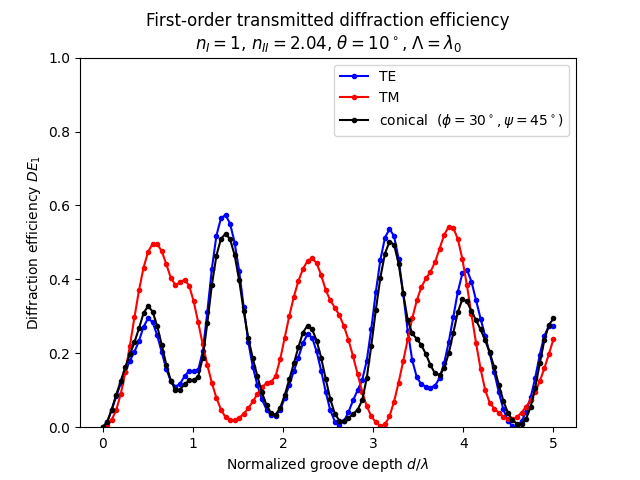
つぎに条件を変更したtest02.pyとの差分を示します。
$ diff test01.py test02.py
72c72
< depths = numpy.linspace(0.,5.,100)*wavelength
---
> depths = numpy.linspace(45.,50.,100)*wavelength
test02.py の実行結果
test02.pyの実行結果を以下にしめします。
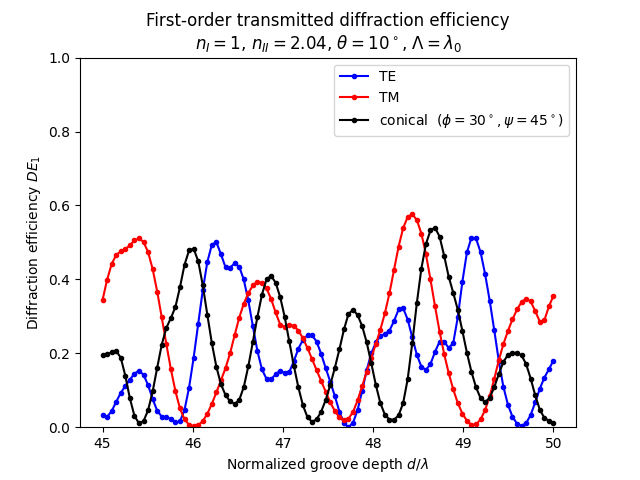
つぎに条件を変更したtest03.pyとの差分を示します。
68c68
< multiplier = 1
---
> multiplier = 10
test03.py の実行結果
test03.pyの実行結果を以下に示します。
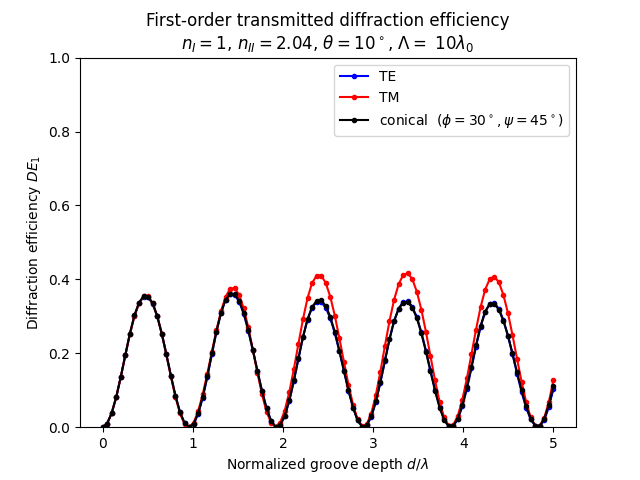
最後に4つ目の、test04.pyとの差分を示します。
$ diff test01.py test04.py
68c68
< multiplier = 1
---
> multiplier = 10
72c72
< depths = numpy.linspace(0.,5.,100)*wavelength
---
> depths = numpy.linspace(45.,50.,100)*wavelength
test04.py の実行結果
test04.pyの実行結果を以下に示します。
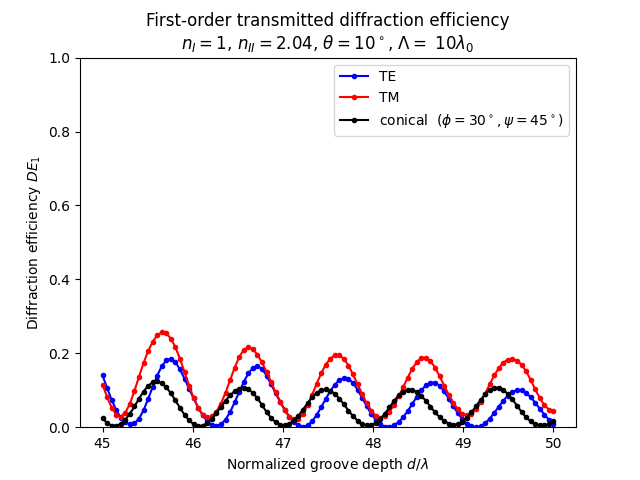
まとめ
- Rodisのソースコードの改修方法を紹介しました。
- 改修したRodisを用いてMoharamの論文の例題を実行し、解析結果を示しました。
- 解析結果は 1次元の格子に対して、TE,TMおよびConicalのそれぞれの光入射条件でMoharamの論文の特性をほぼ再現しました。
参考文献
- M. G. Moharam, E. B. Grann, D. A. Pommet, and T. K. Gaylord, “Formulation for stable and efficient implementation of the rigorous coupled-wave analysis of binary gratings,” J. Opt. Soc. Am. A 12(5), pp. 1068–1076, 1995
Discussion