【OR】線形計画法の第一歩:タブローによるシンプレックス解法
はじめに
この記事では、初学者向けに線形計画法の解法の一つであるタブローを利用したシンプレックス法について解説します。
対象読者
- とりあえずシンプレックス法による線形計画問題を解けるようになりたい方
シンプレックス法とは?
シンプレックス法の概要
シンプレックス法は、線形計画法において最適解を求めるための代表的な手法の一つです。線形計画法の特徴として、最適解は実行可能領域の端点(頂点)に存在することが知られています。シンプレックス法は、この特性を利用して実行可能領域の端点を巡りながら最適解を探索するアルゴリズムです。

この図は、シンプレックス法がどのようにして実行可能領域の頂点を巡りながら最適解を探索するかを示しています。赤い矢印は、シンプレックス法の各ステップでの移動を表しています。
シンプレックス法の基本概念
制約条件と目的関数
- 目的関数: 最大化・最小化したい量を表す線形関数
- 制約条件: 利用可能なリソースやその他の制限を表す一連の線形等式や不等式
具体例
製品生産の最適化問題
原材料AとBがあり、原材料Aは
製品Aを作るのに原材料AとBそれぞれ
また、製品Aが1単位あたり3万円、製品Bが1単位あたり2万円の利益を生み出すことができます。
これらを目的関数と制約条件にて整理します:
x: 製品Aの生産量(単位)
y: 製品Bの生産量(単位)
z: 総利益(万円)
目的関数:
制約条件:
このような制約条件下でxとyそれぞれ何個生産すれば利益を最大化することができるかを求めていきます。
標準形
線形計画問題を形式的に記述するためには、標準形に変換する必要があります。標準形は次のように構成されます。
- 目的関数の最大化または最小化
- 等式制約条件
- 非負の変数条件
製品生産の最適化問題を標準形に変換すると、次のようになります。
具体例
上記の例の問題を標準形に変換します。
目的関数:
制約条件:
非負制約:
さらに、スラック変数(後ほど説明)を導入し、不等式から等式に変換する
制約条件(等式):
最終的に以下のようになります。
目的関数:
制約条件(等式):
非負制約:
スラック変数
不等式制約条件式から等式制約条件式に変換するために導入される非負な補助変数のことです。
辞書(シンプレックス辞書)
目的: シンプレックス法の各ステップで現在地点での解を管理するために使用する表現方法です。
構成: 基底変数と非基底変数にわけて表現された目的関数と制約条件で構成されます。
具体例
標準形で挙げた例を利用します。
目的関数:
制約条件:
非負制約:
初期辞書
何も操作されていない初期状態の辞書を初期辞書と呼ばれます。
基底変数と非基底変数
辞書表現をした際に左辺にある変数を基底変数、右辺にある変数を非基底変数と呼びます。
基底解
辞書表現において、基底変数と非基底変数を合わせて非基底変数を全て0にして得られる解を基底解と呼びます。
具体例
ピボット操作
辞書の基底解から別の基底解を探すために行う操作のことです。
最適解に向かって解を入れ替えながら探索していきます。
タブロー (Tableau)
シンプレックス法を適用する際に用いる計算表であり、線形計画問題の各ステップを効率的に計算するための表です。
タブローを使ったシンプレックス法の手順
1.初期辞書から表に値を入れ込んでいきます。
- Basisは基底変数を表します。
- CBは基底変数に対応する目的関数の係数を示します。(初期段階では0となります)
- Bは基底変数の値を表します。
- zjは現在の基底変数に基づいて目的関数の係数の合計を示しています。これにより、現在の解がどれだけ目的関数に寄与しているかを評価するために使用されます。
z_j = ∑(CB_i\times a_{ij}) - cj - zjの行ではどの変数を基底に加えるべきか、どの変数を除外すべきかを判断します。要するにピボット操作をするべきかの判断とどの行を対照するべきかを決定するために利用します。

-
ピボット操作
ピボット要素を決定する- ピボット列の選択
-
Cj - Zj - 例:
Cj - Zj = (3, 1)
- 選択した列をピボット列と言います。
-
- ピボット行の選択
- ピボット列の各値に対してB列の各値の比率を計算します。この比率が最小の非負数を持つ行をピボット行として選択します。
- 例: ピボット列の値が
(s_1, s_2) = (1, 1) s_2 - 選択された行をピボット行と言います。
- ピボット行とピボット列の交差点の要素をピボット要素としてピボット操作を行います。

基底変数の置き換えと基底変数に対応する目的関数の係数を置き換える
- ピボット列の目的関数のxをピボット行の基底変数にセットし、xの係数を基底変数に対応する目的関数の係数の箇所にセットします。
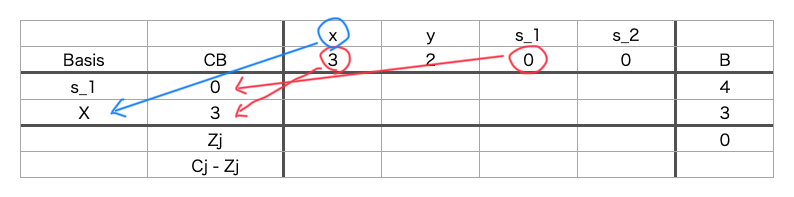
ピボット列を単位列にする
- ピボット要素を1にする
- ピボット行全体をピボット要素で割り、ピボット要素を1にします。
- ピボット列の他の要素を0にする:
- ピボット行以外の行に対して、ピボット列の要素を0にします。具体的には、他の行のピボット列の値にピボット行を調整して引くことで実現します。
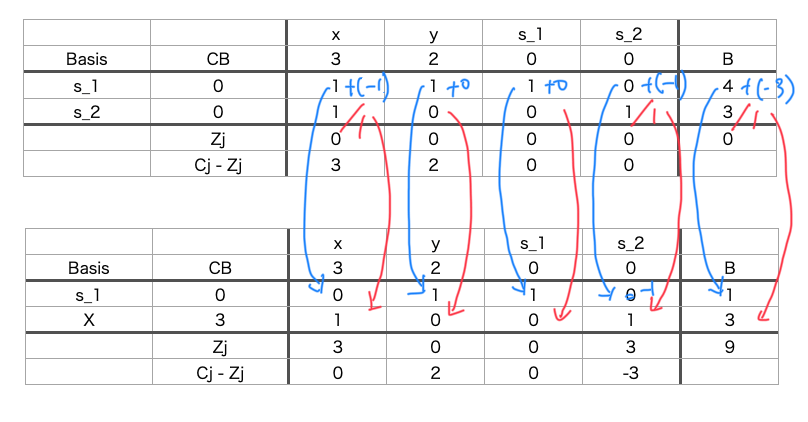
- ピボット列の選択
-
判定
最適解を得るにはC_j - Z_j
ピボット操作基本的に手順は一緒です。ピボット行をyの行に置き換えてピボット操作を行います。
ピボット操作を行った結果以下になりました。
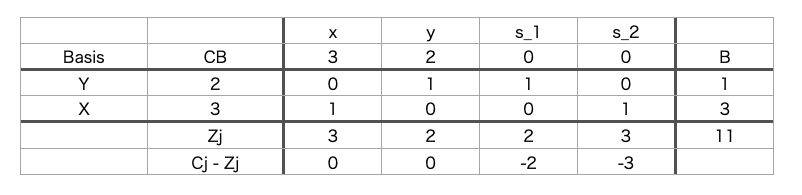
この段階で、
表より、Bは基底変数の値を表すことから
また、

さらに、グラフでも示されているように、
最後に
この記事を通じて、シンプレックス法の基本概念とその適用方法について理解を深めることができたでしょうか。私自身もまだまだですが、上記の方法でシンプレックス法を理解することができました。
今回の解説では、具体的な例を通じてシンプレックス法の手順を一歩一歩説明しました。初めて学ぶ方でも、この記事を参考にすればシンプレックス法を使って実際の問題を解くことができるはずです。さらに理解を深めるためには、実際に手を動かして問題を解いてみてください。
シンプレックス法に関する疑問や質問があれば、ぜひコメント欄で共有してください。また、誤りがあればどしどしご指摘をお願いします。
最後まで読んでいただき、ありがとうございました!
Discussion