テンソルネットワークで計算する量子ゲート方式

本記事は量子コンピューター Advent Calendar 2023の20日目の記事です。

本記事では量子ゲート方式について、ある程度理解していることを前提とします。

量子ゲート方式の原理については以下の記事を参照してください。
https://zenn.dev/torataro/articles/2023-01-05-quantum_circuit
https://zenn.dev/torataro/articles/2023-01-16-quantum_circuit

テンソルネットワークについて

テンソルとは？

テンソルネットワークにおけるテンソルとは多次元配列のことを指します。例えばスカラー、ベクトル、行列は$c,\vec{v},A$と書かれることが多いですが、ベクトルと行列については、

$$\vec{v} = (v_{0}\cdots v_{i}\cdots v_{n-1})^{\top},\; A = \begin{pmatrix} A_{00} & \cdots & A_{0j} & \cdots & A_{0m-1} \\ \vdots & \ddots & \vdots & \ddots & \vdots \\ A_{i0} & \cdots & A_{ij} & \cdots & A_{im-1} \\ \vdots & \ddots & \vdots & \ddots & \vdots \\ A_{n-10} & \cdots & A_{n-1j} & \cdots & A_{n-1m-1} \\ \end{pmatrix}$$

とその要素も書き下すことでより丁寧な表現になります。ただこのように毎度要素も書き下しているようだとページ内を占有してしまいます。そこで要素の一つを代表させてベクトルならば$v_{i}$、行列ならば$A_{ij}$で表してしまうことがあります。これがテンソルです。

テンソルは添え字（$v_{i}$ならば$i$のこと）をつけることで表現されます。添え字は脚と呼ばれ、ベクトル$v_{i}$ならば1脚テンソル、行列$A_{ij}$ならば2脚テンソルと呼ばれます。逆に脚を持たない0脚テンソルはスカラー$c$のことです。この脚をたくさん増やせば$n$脚の場合、

$$T_{i_{1}i_{2}\cdots i_{n}}$$

は$n$脚テンソルと呼ばれます。

テンソルのダイアグラム表現

行列をベクトルに作用させたり、内積をとるなどの計算は、テンソルをダイアグラム（図式）で表現することで視覚的に理解できるようになります。ベースとなるのはスカラーです。スカラーを図で表すならば次のような形になります。

続いてベクトルです。ベクトルはこのスカラーに対して脚を一本追加します。脚の名前はなんでも良いですが、ベクトルの要素を$v_{j}$と書くとして、ここでは$j$と置きます。

行列はさらに脚が二本になります。行列の要素は$A_{ij}$と書かれるとします。

そのほかのテンソルも脚の数と同じ分だけ図上でも脚を設置していけば、テンソルをダイアグラム化することができます。次にこのダイアグラムを使って計算したいと思います。実行する計算は次のものです。

$$\vec{w}=A\vec{v}$$

この時の結果はベクトル$\vec{w}$になることに意識してください。これをテンソルで記述するならば、

$$w_{i}=\sum_{j}A_{ij}v_{j}$$

となります。この式の右辺はダイアグラム上だと、

と書かれます。つまり行列$A$とベクトル$\vec{v}$が共通して持つ脚$j$を結合させてしまうのです^[1]。結合した個所は一つにまとめることができます。

結果、残る脚は一本となりダイアグラム上でベクトルが新たに出来上がる様子が見て取れます。このように共通した脚$j$で一つにまとめる（数式上は総和をとる）ことを縮約をとると呼びます。他にも内積をとる、トレースを計算するなどは次のように表現することができます。

テンソルの縮約を表現したこれらのダイアグラムはテンソルネットワークと呼ばれます。テンソルネットワークとして有名なものとしてMPSやMERAが挙げられます。ぜひ調べてみてください。

テンソルネットワークの恩恵

テンソルネットワークから得られる恩恵は、メモリ使用量と計算量を見積もれる点にあります。計算量については、小さな計算量で済ませられる方法が見つけられると言ったほうが正確かもしれません（参考文献[1]参照）。ここではメモリ使用量について説明します。

例えばテンソル$T_{ijklmn}$が以下のように分解できたとしましょう。

ここで脚$a$～$e$、$i$～$n$は$\sigma$個の値をとると仮定します（例えば$a=0,1,\cdots,\sigma-1$）。この場合、テンソル$T_{ijklmn}$は$\sigma^{6}$個のパターンの値をメモリに格納する必要があります。しかし分解した後ならば$p_{ia}$と$u_{en}$が$\sigma^{2}$個、$q_{ajb}$～$t_{dme}$が$\sigma^{3}$個の値とるので、$2\sigma^{2}+4\sigma^{3}$個のパターンの値をメモリに格納するだけで良くなります。例えば$\sigma=2$の時、これらのパターン数の比をとれば

$$\frac{2\sigma^{2}+4\sigma^{3}}{\sigma^{6}}=\frac{40}{64}=0.625$$

しっかりとメモリ使用量を削減できていることが確認できます。この$\sigma$が大きくなればなるほどメモリ使用量の違いは顕著に現れます。それぞれの違いをグラフで表したいと思います。

縦軸：対数スケール、青：分解前のパターン数、オレンジ：分解後のパターン数

$\sigma$が大きくなればなるほど分解することによる効果は絶大なものになることがわかります。ただ本記事では$\sigma=2$で十分です。（0と1の二値しか考えないため。）

テンソルネットワークと量子ゲート方式

量子ゲート方式を採用した量子コンピュータはその計算モデルとして量子回路が使われます。例えば以下のようなものです。

量子回路での量子状態ははじめ、すべて0状態の量子ビット$|0\rangle$を初期状態とし、そこから量子ゲートに従ってその状態が変化していきます。量子ゲートをすべて通り終えた量子状態に対して最後に観測を行い、計算結果を得る流れです。

ここで古典コンピュータで量子ゲート方式の量子コンピュータシミュレーションを行う場合、量子ビットが増えたり、回路が深くなるほどメモリ使用量や計算量が大きくなっていきます。量子状態の時間発展は行列とベクトルの計算になるので、そこにテンソルネットワークを用いることで古典コンピュータでも効率的に計算しようという目論見です。

量子回路のテンソルネットワーク化

1量子ビットの場合

まず1量子ビットの場合を考えます。1量子ビットにおける量子状態$|q\rangle$は

$$|q\rangle=\begin{pmatrix}q_{0} \\ q_{1} \end{pmatrix}$$

という2つの要素を格納するベクトルで、量子ゲートは

$$U=\begin{pmatrix} U_{00} & U_{01} \\ U_{10} & U_{11} \\ \end{pmatrix}$$

という2×2の行列になります。この量子状態$|q\rangle$から量子ゲート$U$が作用する様子は数式上では$U|q\rangle$と書かれるので、これまでの話を踏まえるならばテンソルネットワークでは以下のように書けます。

量子ゲートを次々作用させる場合、量子回路からはどのような順番で量子ゲートが作用するかが確認できます。テンソルネットワーク上でも量子回路が描く順番と同じように量子ゲートを縮約させれば、テンソルネットワークで量子状態が時間発展するという量子回路と同じ解釈をすることができます。つまり量子回路はテンソルネットワーク化することが可能なのです。

多量子ビットの場合

多量子ビットの場合でも一量子ビットの時と変わりません。例えば$n$量子ビットの場合を考えます。この量子状態はテンソル積を使って

$$|q_{n-1}q_{n-2}\cdots q_{0}\rangle:=|q_{n-1}\rangle\otimes|q_{n-2}\rangle\otimes\cdots\otimes|q_{0}\rangle$$

と書けますが、これをテンソルネットワークで描画すると、一例として、

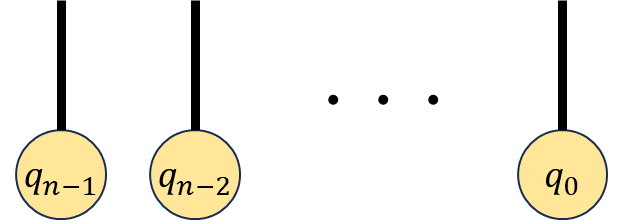
が描けます。これは全体として$n$脚のダイアグラムになります。この量子ビット全体に作用する量子ゲートは各量子ビットと結合する必要があるので、入力出力分を考慮して$2n$個の脚を持つ必要があります。もし結合した場合、以下のようになります。

量子もつれ生成をテンソルネットワークで計算

TensorNetworkライブラリ（Python）

テンソルネットワークをPythonコードとして記述し、量子もつれ状態を生成する量子回路を組みたいと思います。使うライブラリはのGoogle社から提供されているTensorNetworkです↓。
https://github.com/google/TensorNetwork

ドキュメントは↓を参照してください。
https://tensornetwork.readthedocs.io/en/latest/

このライブラリの使い方を説明します。実行環境はJupyter Notebookを想定します。TensorNetworkは以下のコマンドでインストールしてください。

!pip install tensornetwork

またnumpyも使うので入っていなければ適宜インストールお願いします。

TensorNetworkの使い方を簡単に説明します。必要な手順は以下の三つです。

1. ノード（Node）の定義
2. エッジ（Edge）の結合
3. テンソルの縮約

ノードとはテンソルやエッジが定義されているオブジェクトを指します。エッジとはテンソルの脚を指します。例として次の計算を実行してみましょう。

$$w_{i}=\sum_{j}A_{ij}v_{j}$$

これは初めに紹介した$\vec{w}=A\vec{v}$という計算です。$\vec{v}$、$A$、$\vec{w}$は、

$$\vec{v}=\begin{pmatrix}1 \\ 2 \end{pmatrix},\; A=\begin{pmatrix} 1 & 2 \\ 3 & 4 \\ \end{pmatrix},\; \vec{w}=A\vec{v}=\begin{pmatrix}5 \\ 11 \end{pmatrix}$$

とします。

1. ノード（Node）の定義

ベクトル$\vec{v}$と行列$A$のノードの定義を行います。

import numpy as np
import tensornetwork as tn # TensorNetworkライブラリのインポート

v = np.array([1,2]) # ベクトルvの定義
A = np.array([[1,2],[3,4]]) # 行列Aの定義

v_Node = tn.Node(v, name="vector_v") # ベクトルvのノードの定義
A_Node = tn.Node(A, name="matrix_A") # 行列Aのノードの定義

ndarrayとして予め宣言したvとAに対して、tn.Nodeでノードが定義されます。ここで

A_Node

と単体でA_Nodeを実行してみてください。結果として以下のものが得られるはずです。

Node
(
name : 'matrix_A',
tensor : 
array([[1, 2],
       [3, 4]]),
edges : 
[
Edge(Dangling Edge)[0] 
, 
Edge(Dangling Edge)[1] 
] 
)

定義したノードの中にname="matrix_A"として与えたノードの名前nameやテンソルtensor、テンソルの脚のリストedgesが格納されているのが確認できます。試しに

A_Node.tensor

を実行してみてください。結果として

array([[1, 2],
       [3, 4]])

が出力されるはずです。これは初めに宣言した行列$A$のndarrayです。次にエッジについてです。Edge(Dangling Edge)[0]にアクセスするならばA_Node.edges[0]でも可能ですが、.edgesの部分は省略して、

A_Node[0]

で簡潔に書くことができます。試しに実行してみてください。所望の結果が得られるはずです。数式とエッジ指定方法の対応ですが、$A_{ij}$については次の表のようになっています。

テンソルの脚	指定方法
$i$	A_Node[0]
$j$	A_Node[1]

2. エッジ（Edge）の結合

$v_{j}$と$A_{ij}$の脚$j$を結合しましょう。$A_{ij}$の$j$に対応するエッジはA_Node[1]、$v_{j}$はv_Node[0]です。これらは次のように結合します。

connect = tn.connect(A_Node[1], v_Node[0])

これで完了です^[2]。

3. テンソルの縮約

最後に結合した脚で縮約をとります。次の通りです。

w_Node = tn.contract(connect)

w_Nodeはベクトル$\vec{w}$をノード化したものです。この計算の後、

w_Node.tensor

を実行すると所望する結果

array([ 5, 11])

が得られます。これが一連の流れになります。これまでのコードのまとめをおいておきます。

一連のコード

import numpy as np
import tensornetwork as tn # TensorNetworkライブラリのインポート

v = np.array([1,2]) # ベクトルvの定義
A = np.array([[1,2],[3,4]]) # 行列Aの定義

v_Node = tn.Node(v, name="vector_v") # ベクトルvのノードの定義
A_Node = tn.Node(A, name="matrix_A") # 行列Aのノードの定義

connect = tn.connect(A_Node[1], v_Node[0]) # 脚の結合

w_Node = tn.contract(connect) # 縮約する
w_Node.tensor # 結果表示

縮約をもう少し簡単化する

ここまで例として挙げたベクトルの計算は、縮約させたい脚が$j$の一本しかなかったため、tn.contractで事足りましたが、結合させる脚が複数ある場合、脚の数だけtn.contractを実行させる必要があります。そこで自動的に一気に縮約をとってくれるtn.contractors.autoを紹介します。結合から縮約までの一連の流れは以下の通りです。

tn.connect(A_Node[1], v_Node[0]) # 脚の結合

w_Node = tn.contractors.auto( # 縮約する
    nodes=[v_Node, A_Node],
    output_edge_order=[A_Node[0]]
)
w_Node.tensor # 結果表示

nodesには縮約対象となるノードのリストを指定します。output_edge_orderには縮約後も縮約結果として残るエッジのリストを指定します。この例ではA_Node[0]つまり$i$がそのまま$w_{i}$の脚になるので、output_edge_orderにA_Node[0]が指定されています。

tn.contractors.autoを使った際の一連の流れのコードをおいておきます。

一連のコード

import numpy as np
import tensornetwork as tn # TensorNetworkライブラリのインポート

v = np.array([1,2]) # ベクトルvの定義
A = np.array([[1,2],[3,4]]) # 行列Aの定義

v_Node = tn.Node(v, name="vector_v") # ベクトルvのノードの定義
A_Node = tn.Node(A, name="matrix_A") # 行列Aのノードの定義

tn.connect(A_Node[1], v_Node[0]) # 脚の結合

w_Node = tn.contractors.auto( # 縮約する
    nodes=[v_Node, A_Node],
    output_edge_order=[A_Node[0]]
)
w_Node.tensor # 結果表示

量子もつれ生成をテンソルネットワークで計算

では本題です。2量子ビットの量子もつれ状態を生成してみましょう。初期状態は次の通りです。

$$|q_{1}q_{0}\rangle=|00\rangle$$

生成する量子もつれ状態は次の通りです。

$$\frac{1}{\sqrt{2}}\left(|00\rangle+|11\rangle\right)$$

$|q'_{1}q'_{0}\rangle$を観測する量子状態とするならば$|q'_{1}q'_{0}\rangle=|00\rangle,|11\rangle$は$1/2$、$|q'_{1}q'_{0}\rangle=|01\rangle,|10\rangle$は$0$の確率で観測されることが確認できれば良いです。このもつれ状態はアダマールゲート$H$とCXゲート$CX$を作用させることで生成でき、観測も含めた量子回路は次の通りです。

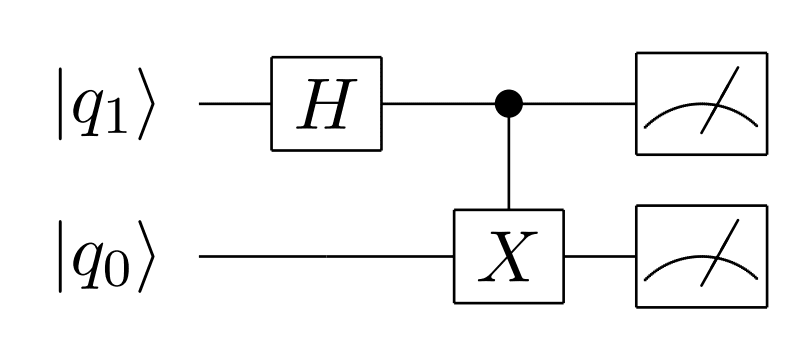
この量子回路をテンソルネットワーク化することを考えるならば、$|q_{1}\rangle,|q_{0}\rangle,|q_{1}'\rangle,|q_{0}'\rangle$は1脚、$H$は2脚、$CX$は4脚のテンソルとなるので、

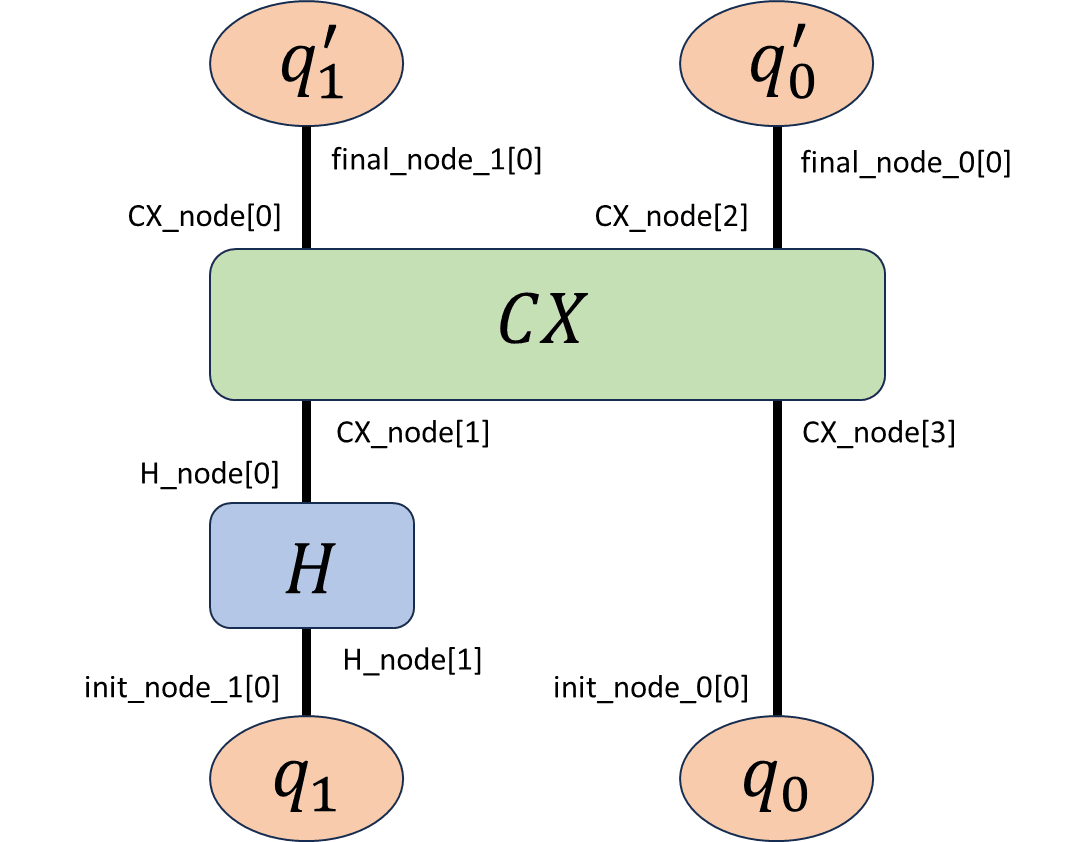
エッジの指定方法付き（後述の量子もつれ状態生成コードにて使用）

と書くことができます。この量子回路全体を$U$と置けば$|q_{1}'q_{0}'\rangle$という状態を観測するための確率振幅$\alpha(q_{1}'q_{0}')$は、

$$\alpha(q_{1}'q_{0}')=\langle q_{1}'q_{0}'|U|q_{1}q_{0}\rangle$$

となります。この確率振幅の大きさの二乗$\lvert\alpha(q_{1}'q_{0}')\rvert^{2}$を求めることで、状態$|q_{1}'q_{0}'\rangle$を観測する確率が得られます。この確率振幅をテンソルネットワークとして記述したのが上で紹介したテンソルネットワークであり、TensorNetworkを使ってコード化したのが以下のものです。

量子もつれ状態生成コード

import numpy as np
import tensornetwork as tn

O  = np.array([[0, 0],[0, 0]]) 
I  = np.array([[1, 0],[0, 1]])
X  = np.array([[0, 1],[1, 0]])
H  = np.array([[1, 1],[1,-1]]) / np.sqrt(2) # アダマールゲート定義
CX = np.array([[I, O],[O, X]]) # CXゲート定義
zero_state = np.array([1, 0]) # |0>状態定義
one_state  = np.array([0, 1]) # |1>状態定義

H_node  = tn.Node(H, name="Hadamard Gate") # アダマールゲートノード化
CX_node = tn.Node(CX, name="Controlled NOT Gate") # CXゲートノード化
init_node_1 = tn.Node(zero_state, name="zero_init_state") # 初期状態|q_1>=|0>ノード化
init_node_0 = tn.Node(zero_state, name="zero_init_state") # 初期状態|q_0>=|0>ノード化
zero_final_node_1 = tn.Node(zero_state, name="zero_final_state") # 終状態|q'_1>=|0>ノード化
zero_final_node_0 = tn.Node(zero_state, name="zero_final_state") # 終状態|q'_0>=|0>ノード化
one_final_node_1  = tn.Node(one_state, name="one_final_state") # 終状態|q'_1>=|1>ノード化
one_final_node_0  = tn.Node(one_state, name="one_final_state") # 終状態|q'_0>=|1>ノード化

final_node_1 = zero_final_node_1 # 終状態の設定|q'_1>
final_node_0 = zero_final_node_0 # 終状態の設定|q'_0>

# |q_1>から|q'_1>までの脚の結合
tn.connect(H_node[1], init_node_1[0])   # 初期状態|q_1>とアダマールゲートの結合
tn.connect(CX_node[1], H_node[0])       # アダマールゲートとCXゲートの結合
tn.connect(final_node_1[0], CX_node[0]) # CXゲートと終状態|q'_1>の結合
# |q_0>から|q'_0>までの脚の結合
tn.connect(CX_node[3], init_node_0[0])  # 初期状態|q_0>とCXゲートの結合
tn.connect(final_node_0[0], CX_node[2]) # CXゲートと終状態|q'_0>の結合

# 縮約
result = tn.contractors.auto(
    [init_node_1, init_node_0, H_node, CX_node, final_node_1, final_node_0]
)

# 確率計算
np.abs(result.tensor)**2

final_node_1が$|q'_{1}\rangle$、final_node_0が$|q'_{0}\rangle$の状態を表します。この変数に$|0\rangle$状態を表すzero_final_node_1 zero_final_node_0、$|1\rangle$状態を表すone_final_node_1 one_final_node_0を代入することで

$$|q'_{1}q'_{0}\rangle=|00\rangle,|01\rangle,|10\rangle,|11\rangle$$

の4パターンを観測する確率が計算できます。計算結果を共有します。

観測した量子状態$|q'_{1}q'_{0}\rangle$	TensorNetworkで計算した確率	正解の確率
$|00\rangle$	0.4999999999999999	1/2
$|01\rangle$	0.0	0
$|10\rangle$	0.0	0
$|11\rangle$	0.4999999999999999	1/2

正解の確率と同じ結果が得られていることが確認できます^[3]。

最後に

一通り量子回路をテンソルネットワークで記述するところまで説明ができました。本当は説明したりない箇所がいくつかあったりするのですが、これ以上記述すると記事が長くなってしまうので一旦ここで終わらせておきます。最後まで読んでいただきありがとうございました！

追記：量子もつれ状態生成とそれを観測するコードを↓に格納しています。
https://github.com/torataro-tiger/tensor_network_for_quantum_computing

Appendix

参考文献

[1] 西野 友年（著）「テンソルネットワーク入門」株式会社講談社サイエンティフィク
[2] 量子ソフトウェア産学協働ゼミ https://github.com/utokyo-qsw/joint-seminar

実行環境

OS: Windows 11
Python: 3.10.6
notebook: 7.0.6
tensornetwork: 0.4.6
numpy: 1.26.2

脚注

1. 「結合させること」=「縮約（後述）を取る」と解釈する場合があります。本記事ではダイアグラム上で脚と脚がくっついているだけで、この時点では縮約は取っていないことに注意してください。

2. ちなみにconnect = A_Node[1] ^ v_Node[0]という書き方も可能です。これを実行する場合はimport numpyの箇所から再実行してください。connect = tn.connect(A_Node[1], v_Node[0])を実行してからconnect = A_Node[1] ^ v_Node[0]を実行するとすでにエッジが結合しているためエラーを吐きます。

3. 実は確率を得るだけならば$|q'_{1}q'_{0}\rangle$での縮約までとる必要はないんですが、$|q'_{1}q'_{0}\rangle$という状態を観測することを実感してもらうため$|q'_{1}q'_{0}\rangle$の縮約も含めています。