はじめに
本記事は量子回路を理解しよう!part1(量子ビットまで)の続きです。
今回から数式ベースでの記述になりますが、難易度が上がるわけではありませんので、
是非お付き合いください!
テンソル積
2量子ビットの表現
part1の最後では1量子ビットにおける量子計算を体験しました。しかしこれは実用的ではありません。そこで試しに量子ビットをもう一つ増やして2量子ビットだったらどうなるか考えてみましょう。まず2進数における10進数との対比は次の通りでした。
00_{(2)}=0_{(10)},\,
01_{(2)}=1_{(10)},\,
10_{(2)}=2_{(10)},\,
11_{(2)}=3_{(10)}\,
下添字の()はそれが2進数か10進数かを表しています。これらからビットをもう一つ増やすことで0から3の4パターンを表現できることが確認できました。量子力学における状態はベクトルで表現されることを思い出しましょう。このとき2量子ビットを表すベクトルは次で定義できそうです。
|0\rangle = |00\rangle = \begin{pmatrix}1 \\ 0 \\ 0 \\ 0\end{pmatrix},\,
|1\rangle = |01\rangle = \begin{pmatrix}0 \\ 1 \\ 0 \\ 0\end{pmatrix},\,
|2\rangle = |10\rangle = \begin{pmatrix}0 \\ 0 \\ 1 \\ 0\end{pmatrix},\,
|3\rangle = |11\rangle = \begin{pmatrix}0 \\ 0 \\ 0 \\ 1\end{pmatrix}\,
これが2量子ビットの表現で、1量子ビットでは0と1の重ね合わせだったのに対し、任意の2量子ビットでは
|q\rangle=a|00\rangle+b|01\rangle+c|10\rangle+d|11\rangle=\begin{pmatrix}a \\ b \\ c \\ d\end{pmatrix}
と4つのベクトルの重ね合わせで表現できます。例のごとく係数a,b,c,dはその大きさの二乗を計算すると、各量子ビットが観測される確率になります。
ここまで1量子ビットと2量子ビットの接点について記述してきませんでしたが、1量子ビットから2量子ビットを生成することができます。それはこんな演算になります。まず二つのq_{0}とq_{1}という1量子ビットのベクトルを定義します。
|q_{0}\rangle=\begin{pmatrix}a_{0} \\ b_{0} \end{pmatrix},
|q_{1}\rangle=\begin{pmatrix}a_{1} \\ b_{1} \end{pmatrix}
ここでq_{1}の要素にq_{0}を作用させることを\otimesで表現しましょう。
|q_{1}\rangle\otimes|q_{0}\rangle=
\begin{pmatrix}a_{1}|q_{0}\rangle \\ b_{1}|q_{0}\rangle \end{pmatrix}=
\begin{pmatrix}a_{1}\begin{pmatrix}a_{0} \\ b_{0} \end{pmatrix} \\ b_{1}\begin{pmatrix}a_{0} \\ b_{0} \end{pmatrix} \end{pmatrix}=
\begin{pmatrix}a_{1}a_{0} \\ a_{1}b_{0} \\ b_{1}a_{0} \\ b_{1}b_{0} \end{pmatrix}
はじめ2つの要素しか持たなかったベクトルから4つの要素を持つベクトルが生成できました。このようにベクトルの要素を拡張する演算をテンソル積といいます。量子力学におけるテンソル積の流儀として
|q_{1}q_{0}\rangle=|q_{1}\rangle|q_{0}\rangle=|q_{1}\rangle\otimes|q_{0}\rangle
と書かれることもよくあります。ここから各1量子ビットは|0\rangle=\begin{pmatrix}1 \\ 0 \end{pmatrix},|1\rangle=\begin{pmatrix}0 \\ 1 \end{pmatrix}であることを思い出せば、実は
|00\rangle=|0\rangle\otimes|0\rangle\\
|01\rangle=|0\rangle\otimes|1\rangle\\
|10\rangle=|1\rangle\otimes|0\rangle\\
|11\rangle=|1\rangle\otimes|1\rangle\\
で記述することができます。各2量子ビットの定義とテンソル積の演算から上式が成り立つことを確認してみてください。最後に計算するときに便利なテンソル積の性質を\alpha,\betaという係数を使って紹介します。
|q_{2}\rangle\otimes(\alpha|q_{1}\rangle+\beta|q_{0}\rangle)=
\alpha|q_{2}\rangle\otimes|q_{1}\rangle+\beta|q_{2}\rangle\otimes|q_{0}\rangle
=\alpha|q_{2}q_{1}\rangle+\beta|q_{2}q_{0}\rangle \\
(\alpha|q_{1}\rangle+\beta|q_{0}\rangle)\otimes|q_{2}\rangle=
\alpha|q_{1}\rangle\otimes|q_{2}\rangle+\beta|q_{0}\rangle\otimes|q_{2}\rangle
=\alpha|q_{1}q_{2}\rangle+\beta|q_{0}q_{2}\rangle
実はテンソル積にも掛け算と同じように分配法則が成り立ちます。
2量子ビットにおける量子計算
先ほどベクトルの要素を拡張する操作をテンソル積と紹介しましたが、同様の考え方で行列にも適用されます。まず次のような行列U_{0},U_{1}を定義しましょう。
U_{0} = \begin{pmatrix}
a_{0} & b_{0} \\
c_{0} & d_{0}
\end{pmatrix},\,
U_{1} = \begin{pmatrix}
a_{1} & b_{1} \\
c_{1} & d_{1}
\end{pmatrix},\,
このときU_{1}の各要素にU_{0}を作用させる操作を
U_{1}\otimes U_{0} = \begin{pmatrix}
a_{1}U_{0} & b_{1}U_{0} \\
c_{1}U_{0} & d_{1}U_{0}
\end{pmatrix}=
\begin{pmatrix}
a_{1}\begin{pmatrix}a_{0} & b_{0} \\ c_{0} & d_{0}\end{pmatrix} & b_{1}\begin{pmatrix}a_{0} & b_{0} \\ c_{0} & d_{0}\end{pmatrix} \\
c_{1}\begin{pmatrix}a_{0} & b_{0} \\ c_{0} & d_{0}\end{pmatrix} & d_{1}\begin{pmatrix}a_{0} & b_{0} \\ c_{0} & d_{0}\end{pmatrix}
\end{pmatrix}
より、
U_{1}\otimes U_{0}=\begin{pmatrix}
a_{1}a_{0} & a_{1}b_{0} & b_{1}a_{0} & b_{1}b_{0} \\
a_{1}c_{0} & a_{1}d_{0} & b_{1}c_{0} & b_{1}d_{0} \\
c_{1}a_{0} & c_{1}b_{0} & d_{1}a_{0} & d_{1}b_{0} \\
c_{1}c_{0} & c_{1}d_{0} & d_{1}c_{0} & d_{1}d_{0} \\
\end{pmatrix}
で定義します。これが行列版のテンソル積です。先ほど見たように2量子ビットのベクトルは4つの要素を持つので、それに対応する量子ゲートは4×4の大きさになります。ここから量子ビットがより増えていくと、この行列の大きさも拡大していくため行列の計算がより大変になっていくことが想像できます。しかしテンソル積にはありがたい性質があります。それが次の通りです。
U_{1}\otimes U_{0}|q_{1}q_{0}\rangle=(U_{1}|q_{1}\rangle)\otimes(U_{0}|q_{0}\rangle)
つまり、U_{1}\otimes U_{0}という大きな行列を|q_{1}q_{0}\rangleに作用させた結果は、|q_{1}\rangleにU_{1}を作用させたものと|q_{0}\rangleにU_{0}に作用させたもののテンソル積を取った結果に等しいというのです。これならはじめから2量子ビットの枠組みで考えることなく、1量子ビットで分解してから2量子ビットとして扱えるようになります。この考え方は量子回路を理解するうえで一番重要です。
例としてpart1で扱ったアダマールゲートを挙げましょう。2量子ビット版のアダマールゲートは次の通りです。
H\otimes H = \frac{1}{\sqrt{2^{2}}}\begin{pmatrix}
1 & 1 & 1 & 1 \\
1 & -1 & 1 & -1 \\
1 & 1 & -1 & -1 \\
1 & -1 & -1 & 1 \\
\end{pmatrix}
これを|00\rangleに作用させてみましょう。まず直接計算した結果は、
H\otimes H|00\rangle=\frac{1}{\sqrt{2^{2}}}\begin{pmatrix}
1 & 1 & 1 & 1 \\
1 & -1 & 1 & -1 \\
1 & 1 & -1 & -1 \\
1 & -1 & -1 & 1 \\
\end{pmatrix}
\begin{pmatrix}1 \\ 0 \\ 0 \\ 0\end{pmatrix}
=\frac{1}{\sqrt{2^{2}}}\begin{pmatrix}1 \\ 1 \\ 1 \\ 1\end{pmatrix}
であるので、
H\otimes H|00\rangle=\frac{1}{\sqrt{2^{2}}}(|00\rangle+|01\rangle+|10\rangle+|11\rangle)
となります。つまり2量子ビットになってもアダマールゲートからすべての重ね合わせが生成されることが確認できました。次に先ほど紹介したテンソル積のありがたい性質と、H|0\rangleはpart1で予め計算していたのでこの結果、そしてテンソル積の分配法則を使えば、
\begin{align*}
H\otimes H|00\rangle &= (H|0\rangle)\otimes(H|0\rangle) \\
&= (\frac{1}{\sqrt{2}}|0\rangle+\frac{1}{\sqrt{2}}|1\rangle)\otimes(\frac{1}{\sqrt{2}}|0\rangle+\frac{1}{\sqrt{2}}|1\rangle) \\
&= \frac{1}{\sqrt{2}}|0\rangle\otimes(\frac{1}{\sqrt{2}}|0\rangle+\frac{1}{\sqrt{2}}|1\rangle)+\frac{1}{\sqrt{2}}|1\rangle\otimes(\frac{1}{\sqrt{2}}|0\rangle+\frac{1}{\sqrt{2}}|1\rangle)\\
&=\frac{1}{\sqrt{2^{2}}}(|00\rangle+|01\rangle+|10\rangle+|11\rangle)
\end{align*}
と直接計算した結果と同様の解が得られました!
複数量子ビットへの拡張
なんとなく察しはついていると思いますが、複数量子ビットの場合は次のようにテンソル積でかけ合わせていけばよいです。例えばかけ合わせるベクトルの数がn個あれば
|0\rangle=|0\cdots00\rangle=|0\rangle\otimes\cdots\otimes|0\rangle\otimes|0\rangle\\
|1\rangle=|0\cdots01\rangle=|0\rangle\otimes\cdots\otimes|0\rangle\otimes|1\rangle\\
\vdots\\
|2^{n}-1\rangle=|1\cdots11\rangle=|1\rangle\otimes\cdots\otimes|1\rangle\otimes|1\rangle\\
2^{n}個のビットが表現できるようになり、これはn量子ビットと呼ばれます。n量子ビットにおける任意の状態は、これまでの重ね合わせの議論から総和の記号も使って、
|q\rangle=\sum_{i=0}^{2^{n}-1}c_{i}|i\rangle=\sum_{i_{n-1}=0}^{1}\cdots\sum_{i_{1}=0}^{1}\sum_{i_{0}=0}^{1}c_{i_{n-1}\cdots i_{1}i_{0}}|i_{n-1}\cdots i_{1}i_{0}\rangle
と書けます。iは10進数での表現、i_{n-1}\cdots i_{1}i_{0}は2進数での表現をするのに使いました。また行列との作用に関しても
U_{n-1}\otimes\cdots\otimes U_{1}\otimes U_{0}|q_{n-1}\cdots q_{1}q_{0}\rangle
=(U_{n-1}|q_{n-1}\rangle)\otimes\cdots\otimes(U_{1}|q_{1}\rangle)\otimes(U_{0}|q_{0}\rangle)
のように、2量子ビットのときに紹介したそのまま性質が成り立ちます。さらに同じベクトルや行列どうしのテンソル積は累乗を記述する気持ちで略して書くことがあります。例えばテンソル積で掛け合わせるベクトル、行列の数がm個あれば、
|q\rangle^{\otimes m}=|q\rangle\otimes\cdots\otimes|q\rangle\otimes|q\rangle\\
U^{\otimes m}=U\otimes\cdots\otimes U\otimes U
と書くことがあります。
量子回路を理解しよう!
ようやく量子回路の登場です!量子ゲート方式では沢山の量子ビットに対して量子ゲートと次々と作用させていきます。しかしこの量子ゲートを作用させる様子を数式だけで記述してしまったら、いったい何の計算を行っているのか把握しづらくなってしまうでしょう。この計算の流れをダイアグラム化したものが量子回路になります。簡単な例を次の図でいくつか紹介します。

|q\rangle,|q_{0}\rangle,|q_{1}\rangleは1量子ビットです。
量子回路は左から右へ量子ゲートを作用させる順に記述していきます。例えばU_{b}U_{a}|q\rangleについてですが数式の通りU_{a}を作用させてからU_{b}を作用させます。もちろんこのくらい単純であれば数式を見ても何をしているかが把握できます。量子回路を見てもダイアグラムとしてその作用を把握するのは容易なはずです。
次に上から3番目の例について量子ビットが増えたとき、異なる量子ビットの作用は上下に連ねて記述していきます。テンソル積の性質として複数量子ビットでも1量子ビットに分解できたことを思い出しましょう。各量子ビットとその作用は独立するので量子回路上は別の作用として記述されます。
とは言えども複数量子ビットに作用するゲートは1量子ビットの分解というよりはU_{1}\otimes U_{0}でも4×4の行列でした。これは単純にUと見なすのであれば2量子ビット間の作用として考えられます。これは上から4番目の例のようにゲート自体を複数量子ビットにまたがって記述します。
さてこれらの例から少し発展させて次の量子回路を考えてみましょう。
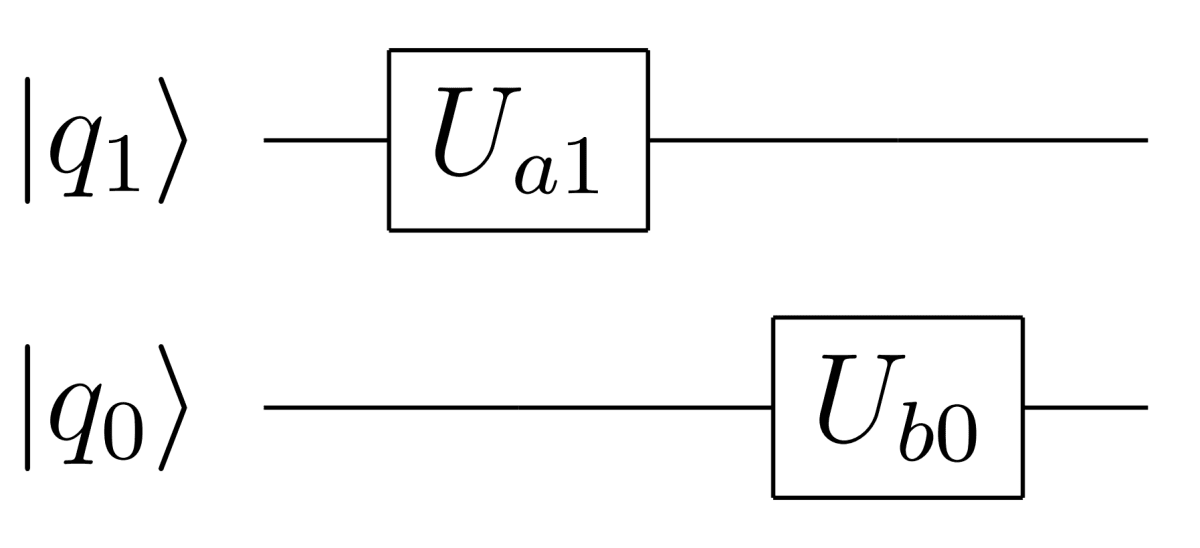
この量子回路の特徴としてはゲートU_{a1}とU_{b0}が同じ列に存在しないということです。ということはU_{a1}とU_{b0}は異なるタイミングで作用することがわかります。これを数式化したらどうなるでしょうか?上記量子回路は丁寧に表すならば次のように書けます。
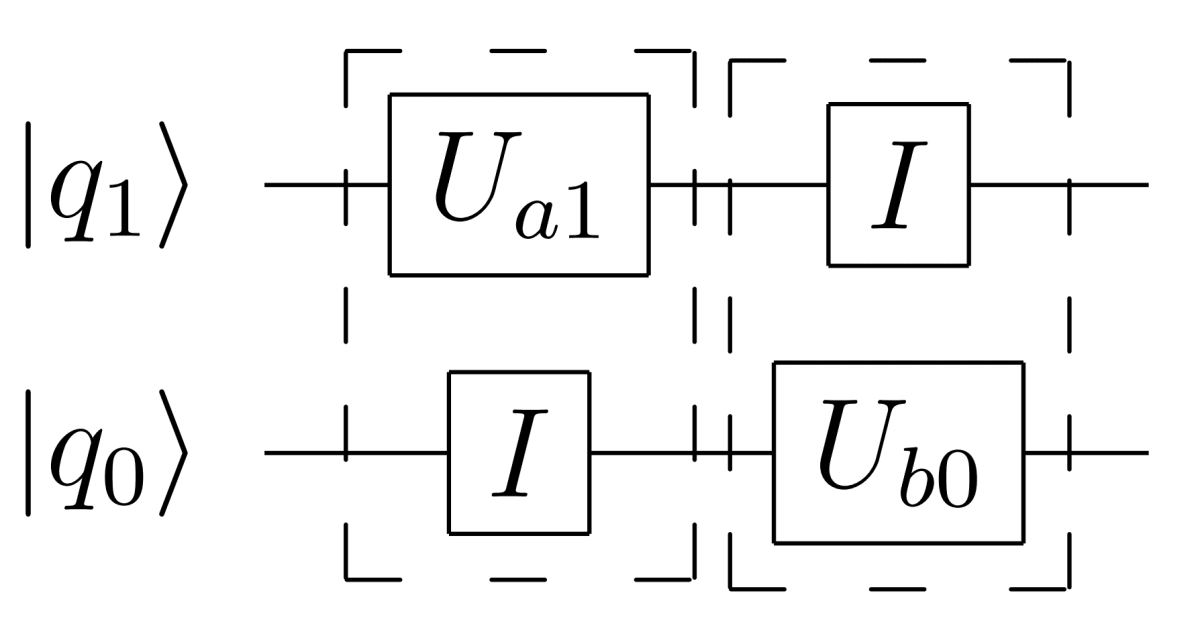
ここでIはなにもしない、つまり|q\rangle=I|q\rangleということを表すゲートで、行列表記するならば、
I=\begin{pmatrix}
1 & 0\\
0 & 1
\end{pmatrix}
という単位行列です。そうするとこれまで紹介してきた例を応用すればこの量子回路は、点線の枠のようにU_{a1}とIが一つのゲート、IとU_{b0}が一つのゲートとしてとらえられるので、
(I\otimes U_{b0})(U_{a1}\otimes I)(|q_{1}\rangle\otimes|q_{0}\rangle)
と数式化することができます。もちろん数式上でも読めばその流れを把握することはできますが、それなら量子回路を見たほうが図としてそのまま理解することができますよね。これが量子回路の魅力です。
さらにその先へ
ここまで量子回路の基礎中の基礎を紹介してきました。もしpart1とpart2で紹介しきれてない項目を取り上げるのであれば、それは
- 複素ベクトルとしての量子ビット
- アダマールゲート以外の量子ゲートの紹介
- さまざまな量子アルゴリズム
でしょうか。part1の脚注でもちょろっと書きましたが、|0\rangleと|1\rangleにかかる係数は複素数です。この複素数を要素とするベクトルは複素ベクトルと呼ばれますが、そこで記述される振幅、位相という波動に由来する量は超重要です。これはブロッホ球と一緒に理解するのがよいでしょう。量子ゲートはこの振幅と位相を変化させて観測する確率を操作するのです。そしてさまざま量子ゲートを設置することで多様な量子アルゴリズムを設計します。
より量子コンピュータについてついて学びたいのであれば、次の参考書を紹介して終わります。ありがとうございました!
- 宮野健次郎・古澤明(著)「量子コンピュータ入門」日本評論社
- 西森秀稔・ 大関真之(著)、 須藤彰三・岡真(監修)「量子アニーリングの基礎 (基本法則から読み解く物理学最前線 18) 」共立出版
- 湊雄一郎・加藤拓己・比嘉恵一朗・永井隆太郎 (著)「IBM Quantumで学ぶ量子コンピュータ」秀和システム


Discussion