シミュレーションで理解するヤングの干渉実験

ヤングの干渉実験

ヤングの干渉実験の対象となる光は波です。波であるならば以下の二つの性質を持ちます。

• 回折：直線的に進むことなく、物体の裏側に回り込みながら伝わっていくこと。
• 干渉：異なる波が重ね合わさり、それぞれが強めあったり弱めあったりすること。

この回折と干渉の原理を通じて光の干渉をスクリーン上に反映させる実験があります。それがヤングの干渉実験と呼ばれるものです。実験系を紹介します。

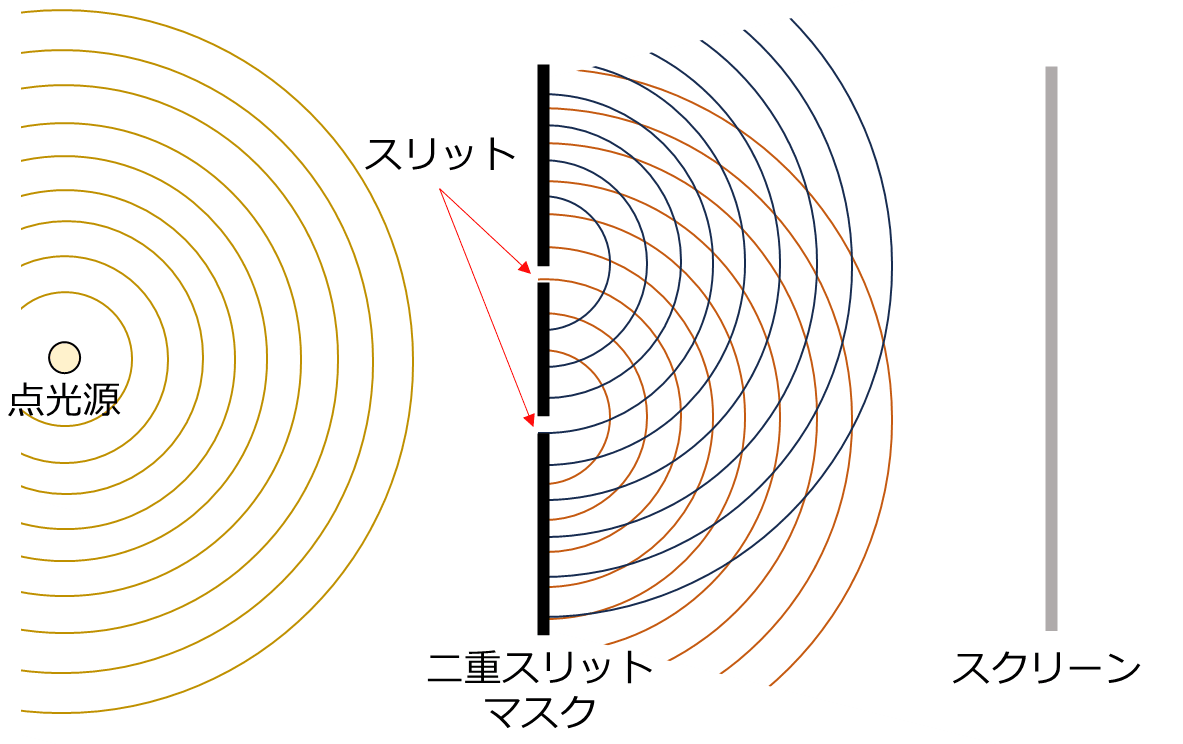
点光源から放たれた光はスリットが二つ設けられている二重スリットマスクまで伝搬し、マスクを通過した光は各々のスリットから回折しながらスクリーンへとさらに伝搬して行く流れです。ここでスクリーンに現れる像を見てましょう。

スクリーン上では明るい部分と暗い部分が交互に現れる干渉縞が確認できます。これは各々のスリットから放たれる光がスクリーン手前で重なり、強めあったり弱めあったことを示しています。この干渉という現象は波の特性であることを踏まえれば、ヤングの干渉実験は光は波であることを明らかにします。

こちらの像はシミュレーションした結果となります。光が波であることを前提にどのように伝搬してこの干渉縞が生じたか、理論的に説明していこうと思います。

光波の伝搬理論

ここから光は波だということを意識して「光」と「光波」を使い分けていこうと思います。

原点は波動方程式

光波$u(\vec{r},t)$は以下の方程式に従います。

$$\nabla^{2}u(\vec{r},t)-\frac{1}{c^{2}}\frac{\partial^{2}u(\vec{r},t)}{\partial t^{2}}=0$$

これは波動方程式と呼ばれ、光波だけでなく音波や弾性波などの重ね合わせの法則を満たす波動の基本的な方程式です。$c$は波が進行する速度で光の場合は光速($=2.998\times 10^{8}\;\text{m/s}$)です。代表的な解としては次の平面波と球面波があります。

・平面波

$$u(\vec{r},t)=A\exp[i(\vec{k}\cdot\vec{r}-\omega t)]$$

・球面波

$$u(\vec{r},t)=\frac{A\exp[i(kr-\omega t)]}{r}\;(r=\lvert\vec{r}\rvert)$$

球面波は再度ホイヘンス・フレネルの原理の説明で現れます。これらの波を見てわかるのは指数関数$\exp$で書かれているということです。波というと正弦波で$\sin$や$\cos$を思い浮かべると思いますが、オイラーの公式から、

$$\exp(i\phi)=\cos(\phi)+i\sin(\phi)$$

より$\exp(i\phi)$で波の振動を表せるので、波動と言われれば複素数の値をとるものだと捉えてください。

この指数関数の性質を使って議論を簡単にしましょう。波動を次のように空間成分$u(\vec{r})$と時間成分$\exp(-i\omega t)$に分解します。

$$u(\vec{r},t)=u(\vec{r})\exp(-i\omega t)$$

平面波や球面波がこの形に分解できるのは明確です。空間成分$u(\vec{r})$も複素数の値をとります。そして単一の周波数をもつ波動はこの形に分解できます^[1]。この式を波動方程式に代入して整理すると、特に空間成分に関して、

$$(\nabla^{2}+k^{2})u(\vec{r})=0\;\left(k=\frac{\omega}{c}\right)$$

という方程式が導けます。これはヘルムホルツ方程式と呼ばれ、これを解くことで光波が空間中でどのように広がるか（伝搬するか）求めることができます。

最後に強度を紹介します。強度は次の定義です。

$$I(\vec{r})=\left\lvert u(\vec{r},t) \right\rvert^{2}=\left\lvert u(\vec{r}) \right\rvert^{2}$$

強度は光のエネルギーを表しており、我々がスクリーン上で観測するものはこの強度になります。

ホイヘンス-フレネルの原理

ヘルムホルツ方程式をベースとして導かれる波動の伝搬結果は次の通りです。

$$u(\vec{r'})=\frac{1}{i\lambda}\iint_{S}u(\vec{r})\frac{\exp\left({ik\mu}\right)}{\mu}\cos\psi dS\;\left(\mu=\lvert\vec{r'}-\vec{r}\rvert\right)$$

これはホイヘンス-フレネルの原理を表した数式です。面$S$は開口で光が通過できる領域を表しています。この領域上の点を$\vec{r}$で表しています。開口$S$の各点から大きさ$u(\vec{r})$^[2]の球面波$\exp(ik\mu)/\mu$が発生し、その球面の重ね合わせ（面積分$\iint_{S}$）によって$\vec{r'}$上に新たな光$u(\vec{r'})$が形成されるとのことです。この説明を図化すると以下のような形です。

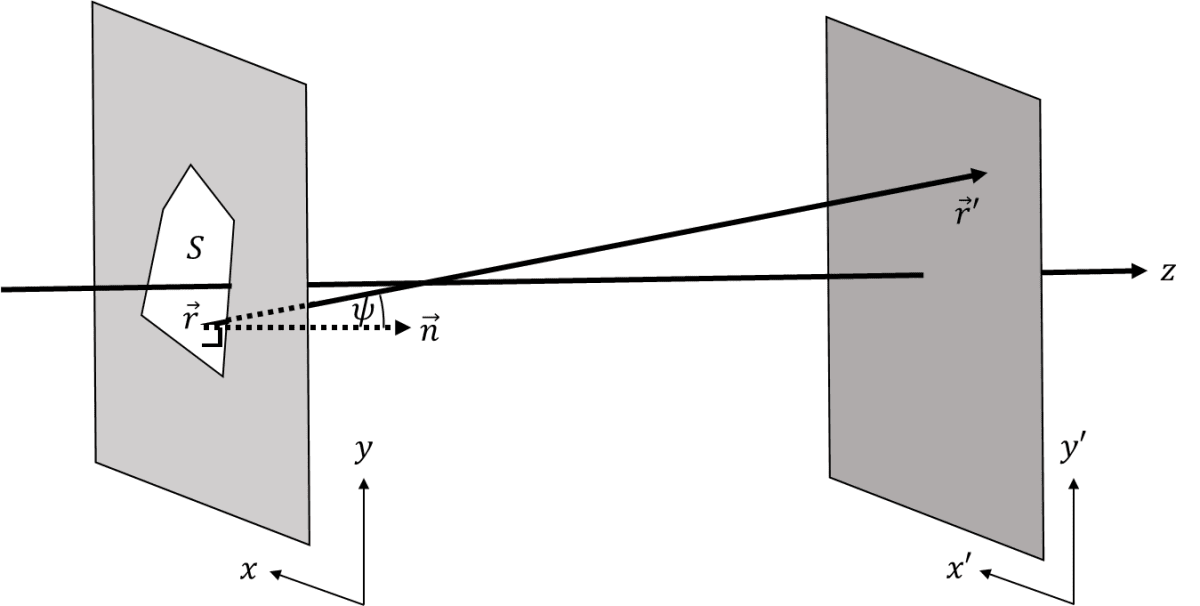
ベクトル$\vec{n}$は面$S$に垂直であり、$\vec{n}$と$\vec{r}'-\vec{r}$がなす角を$\psi$とする。もちろん$z$軸と$\vec{n}$は平行。

物理的な意味を把握するならば、ホイヘンス-フレネルの原理はこの表現で良いですが、光波を解析することを考えるならば、伝搬する方向を明確にしたほうが扱いやすいです。よって伝搬方向を$z$軸と定め、再度ホイヘンス-フレネルの原理を表してみましょう。

$$u(x',y';z)=\frac{z}{i\lambda}\iint_{S}u(x,y;0)\frac{\exp\left({ik\mu}\right)}{\mu^{2}} dxdy$$

$\vec{r}=(x,y,0),\vec{r'}=(x',y',z)$としました。$u(x,y;z)$という表現は$z$地点にて$x,y$平面上に広がる光波を表しています。また$\cos\psi=z/\mu$であり、開口$S$は$z$軸に対して垂直に設置しています。また$dS=dxdy$です。

フレネル回折とフラウンホーファー回折

先ほどの$z$軸方向の伝搬を掘り下げてみましょう。$\mu=\lvert\vec{r'}-\vec{r}\rvert$なので、$u(x',y';z)$は

$$u(x',y';z)=\frac{z}{i\lambda}\iint_{S}u(x,y;0)\frac{\exp\left({ik\sqrt{\left(x'-x\right)^{2}+\left(y'-y\right)^{2}+z^{2}}}\right)}{\left(x'-x\right)^{2}+\left(y'-y\right)^{2}+z^{2}} dxdy$$

と書けます。ここで

$$h(x,y;z)=\frac{z}{i\lambda}\frac{\exp\left({ik\sqrt{x^{2}+y^{2}+z^{2}}}\right)}{x^{2}+y^{2}+z^{2}}$$

を定義すれば、$u(x',y';z)$は、

$$u(x',y';z)=\iint_{S}u(x,y;0)h(x'-x,y'-y;z)dxdy$$

という$u$と$h$の二次元の畳み込み積分で記述できます。本記事では掘り下げませんが、畳み込み積分になるというのは光波をシミュレーションする際、画像処理の知識がそのまま活かせることを意味します。ここでさらに$h(x,y;z)$について$x^{2}+y^{2}\ll z^{2}$という近似を入れると、$u(x',y';z)$は

$$u(x',y';z)=\frac{e^{ikz}}{i\lambda z}\iint_{S}u(x,y;0)\exp\left\lbrace\frac{ik}{2z}[(x'-x)^{2}+(y'-y)^{2}]\right\rbrace dxdy$$

と書けます。この式展開は記事の最後に紹介してある参考文献[1][2]を見てください。この近似に従う伝搬はフレネル回折と呼ばれます。最初に仮定した$x^{2}+y^{2}\ll z^{2}$という近似は近軸近似と呼ばれ、$z$軸周りの$x,y$座標しか考慮しないという意味です。実際に伝搬対象となる光は$z$軸周りにあることがほとんどなので合理的な近似です。ここから伝搬距離$z$を無限遠に飛ばします。この時フレネル回折の式は、

$$u(x',y';z)=C\iint_{S}u(x,y;0)\exp\left[-i\frac{2\pi}{\lambda z}(x'x+y'y)\right]dxdy\;\left(C=\frac{e^{ikz}e^{i\frac{k}{2x}(x'^{2}+y'^{2})}}{i\lambda z}\right)$$

と書けます。この式に従う伝搬はフラウンホーファー回折と呼びます。例えば、はるか遠くの星が放った光が地球に届いたとき、その光はフラウンホーファー回折に従います。ここでさらに、

$$\nu_{x}=\frac{x'}{\lambda z}\;\nu_{y}=\frac{y'}{\lambda z}$$

とおいてやると、フラウンホーファー回折は

$$u(x',y';z)=C\iint_{S}u(x,y;0)\exp\left[-i2\pi(\nu_{x}x+\nu_{y}y)\right]dxdy$$

と書けます。これは$u(x,y;0)$を対象とする二次元のフーリエ変換です。特に$\nu_{x},\nu_{y}$は空間周波数と呼ばれ、単位長さあたりの振動数を表すものです。念のため二次元のフーリエ変換の定義を示すと

$$F(\nu_{x},\nu_{y})=\iint f(x,y)\exp\left[-i2\pi(\nu_{x}x+\nu_{y}y)\right]dxdy$$

であり、フラウンホーファー回折とフーリエ変換が同一であることが確認できます。プログラムとして実行することを考えると、フーリエ変換はライブラリとして提供されているものがいくつもあるので、それをそのまま使えばフラウンホーファー回折は一発でシミュレーションできます。ここから相対的な強度が重要であるという観点から定数$C$は無視して話を展開します。

二重スリットから伝搬する光の解析解

二重スリットとスクリーンの間の距離が十分に離れていると仮定します^[3]。要は二重スリットから伝搬する光はフラウンホーファー回折（二次元フーリエ変換）に従うと仮定するわけです。二重スリットのフーリエ変換は解析的に求めることができ、この解析解を使って後でシミュレーションするフラウンホーファー回折の結果と比較する予定です。まずスリットを表現するために矩形関数を紹介します。矩形関数は次の定義です。

$$\text{rect}\left(\frac{x}{w}\right)= \left\{ \begin{array}{ll} 1 & -w/2<x<w/2 \\ 0 & \text{otherwise} \end{array} \right.$$

図化すると次のような形です。

$w$は矩形関数の窓の大きさを表すことが分かります。これを一次元フーリエ変換すると、

$$\int\text{rect}\left(\frac{x}{w}\right)\exp(-i2\pi\nu_{x} x)dx=w\text{sinc}(w\nu_{x})$$

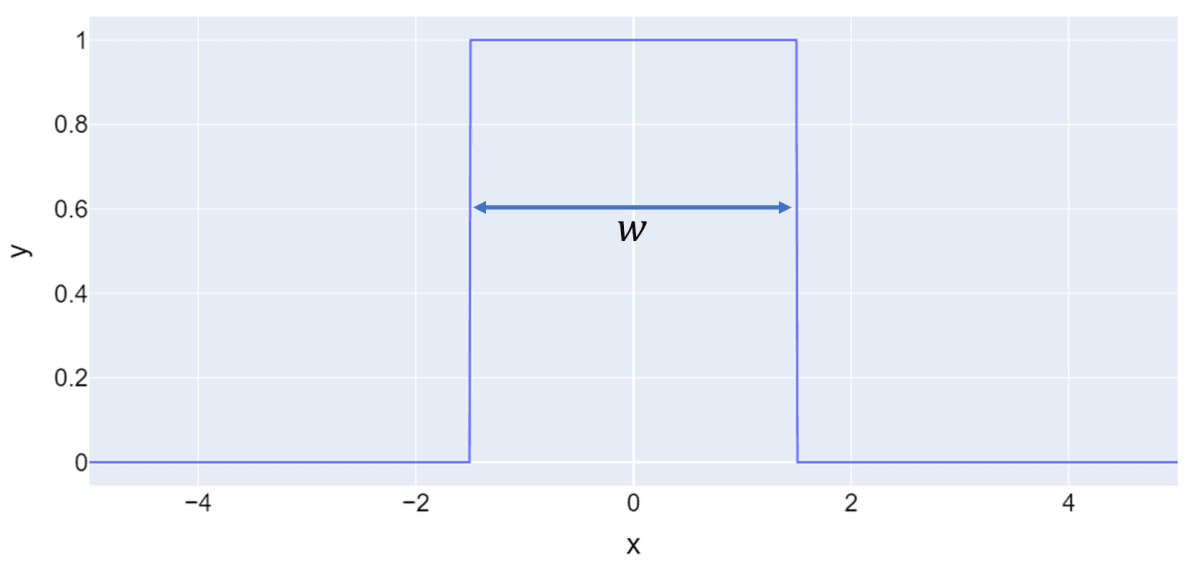
となります。積分範囲は明確にしてませんが$-\infty<x<\infty$です。ここで$\text{sinc}$はシンク関数と呼ばれ、

$$\text{sinc}(x)=\frac{\sin(\pi x)}{\pi x}$$

です^[4]。図化すると次のような概形です。

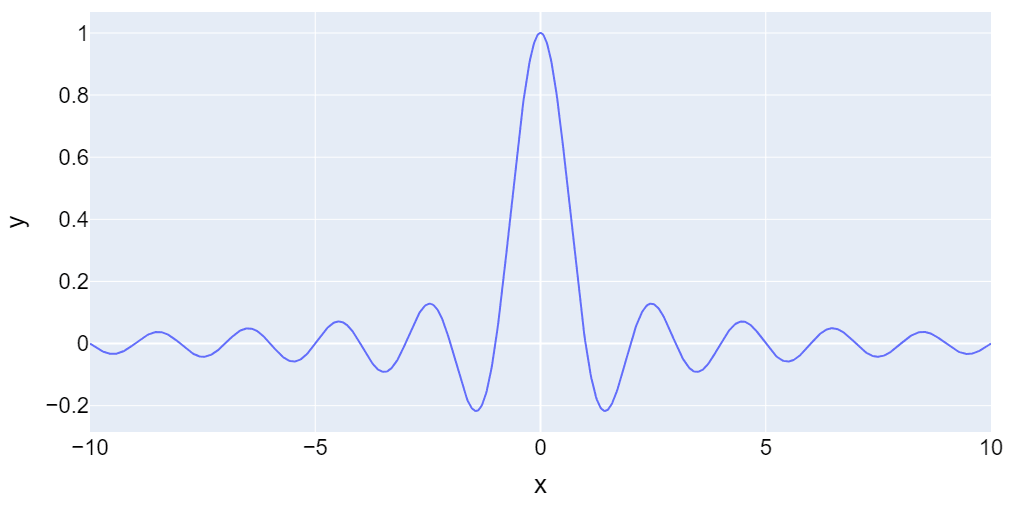
この矩形関数を使うことでスリット一つは$x,y$軸方向の窓の大きさを$w_{x},w_{y}$とすれば、

$$\text{rect}\left(\frac{x}{w_{x}}\right)\text{rect}\left(\frac{y}{w_{y}}\right)$$

と書けます。二重スリットは、各スリットが$D$だけ離れているならば、

$$u(x,y;0)=\left[\text{rect}\left(\frac{x - D/2}{w_{x}}\right)+\text{rect}\left(\frac{x + D/2}{w_{x}}\right)\right]\text{rect}\left(\frac{y}{w_{y}}\right)$$

と書けます。このそして二重スリットからスクリーンまで距離$z=L$のフラウンホーファー回折をしたのならばその結果は$u(x,y;0)$を二次元フーリエ変換することで

$$u(x',y';L)=2w_{x}w_{y}\cos\left(\frac{\pi D x'}{\lambda L}\right)\text{sinc}\left(\frac{w_{x}x'}{\lambda L}\right)\text{sinc}\left(\frac{w_{y}y'}{\lambda L}\right)$$

が得られます。これが求めたかった解析解です。

ヤングの干渉実験のシミュレーション

シミュレーション方法

フラウンホーファー回折のシミュレーションを通じてヤングの干渉実験の結果を得たいと思います。言語はPythonです。まず二重スリットをndarrayで作成します。

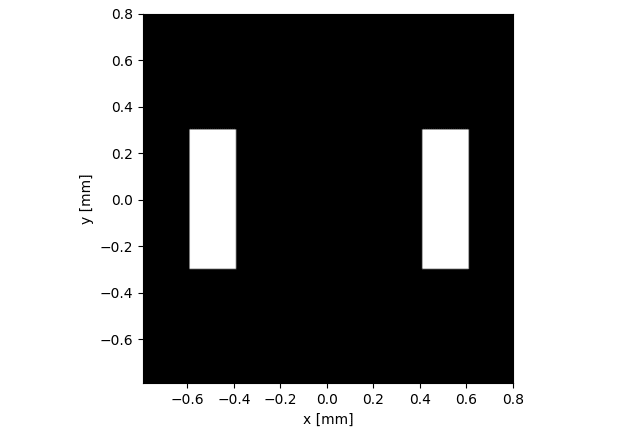
白の領域がスリットでいままで$S$と言っていた開口です。値は$1$を取ります。黒は光を通さない領域です。値は$0$をとります。白と黒の領域を合わせてシミュレーション範囲とします。実際にフラウンホーファー回折のコード部分を見てましょう。

# フーリエ変換を行うモジュールをimport
import numpy.fft as fft

# ここらへん諸々のコード

# フラウンホーファー回折のシミュレーション
result = fft.fftshift(fft.fft2(fft.fftshift(double_slit_mask)))

double_slit_maskは作成した二重スリットマスクです。resultはフラウンホーファー回折した結果です。フラウンホーファー回折はこのように一行で完結させることができます。

このシミュレーション結果をどのように参照しましょうか？resultは複素数を要素とする配列なので分かりやすい結果として何か処理を施す必要があります。スクリーン上に反映されるのは光のエネルギーだと言いました。このresultを光のエネルギーとして見れれば回折結果としてよさそうです。光波$u(\vec{r})$に対してエネルギーに対応するものは、

$$I(\vec{r})=\left\lvert u(\vec{r}) \right\rvert^{2}=u(\vec{r})u^{*}(\vec{r})$$

でした。強度はコード上ではimport numpy as npを宣言したならば、

intensity = np.abs(result)**2

で計算可能です。実際にこの強度分布を見れば干渉縞が確認できます。

シミュレーションと解析解の比較

シミュレーションを行う際、気を付けるべきは以下の二点です。

• 1ピクセル当たりの長さはできるだけ小さくすること。
• 二重スリット周りはできるだけゼロパディングすること。

これらはエイリアシング^[5]を起こさせないかつフラウンホーファー回折後の分解能を高くするために行います。簡単に言えばシミュレーションの精度を上げるためです。今回のシミュレーションにて作成した二重スリットマスクは以下の通りです。

1ピクセルの幅はx軸方向もy軸方向も0.01mmで設定

この時フラウンホーファー回折後に得られる強度像は以下の通りです。

上：シミュレーション結果、下：解析解、右：計算結果拡大、左：計算結果
スクリーンから1m伝搬したと仮定、表示上は白だが波長は赤色(700nm)で計算

こうしてシミュレーション結果と解析解を比較してみると見た感じ同一の結果が得られていることが分かります。このようにして計算機上で干渉縞を得ることが可能です。

最後に

ヤングの干渉実験の傍ら、フラウンホーファー回折のシミュレーション方法も説明しました。今回は解析解があるということでシミュレーションを用いることに疑問はあるかもしれませんが、シミュレーションが本領発揮するのは解析解を持たないときです。いろんな形の開口を作ってそれをフーリエ変換させすればそれは立派なフラウンホーファー回折のシミュレーション結果となります。是非皆さんのほうで試してみてください。

Appendix

参考文献

[1] 谷田貝豊彦（著）「光学」株式会社朝倉書店
[2] Joseph W. Goodman（著）尾崎 義治、朝倉 利光 (訳)「フーリエ光学（第3版）」森北出版株式会社

ソースコード

• 実行環境
  OS: Windows 11
  Python: 3.10.6
  numpy: 1.26.1
  matplotlib: 3.8.1

パラメータ設定の箇所を設定すればいろいろ実験できます。実行する際は自己責任でお願いいたします。

ソースコード

import numpy as np
import numpy.fft as fft
import matplotlib.pyplot as plt

### パラメータ設定（始）###
space_size: float        = 2.5*10 # 伝搬前のxおよびy軸方向の長さ [mm]
pixel_width: float       = 0.01 # 伝搬前の1ピクセルのxおよびy軸の長さ [mm]
wavelength: float        = 700 * 10**(-6) # 波長 [mm]
prop_distance: float     = 1000 # 伝搬距離 [mm]
slit_height: float       = 0.6 # スリットの高さ(y軸方向の長さ)　[mm]
slit_width: float        = 0.2 # [mm] スリットの幅(x軸方向の長さ)　[mm]
slit_distance: float     = 1 # スリット間の幅　[mm]
space_size_expand: float = 6 # 伝搬後強度拡大表示時のxおよびy軸方向の長さ [mm]
### パラメータ設定（終）###

# その他シミュレーション準備
x = np.arange(-space_size / 2, space_size / 2, pixel_width)
number_of_points = len(x)
y = x
xx, yy = np.meshgrid(x, y)

# 二重スリットマスク生成用関数
def generate_double_slit_mask() -> np.ndarray:

    # 一つ目のスリット(x座標がマイナスになる位置に設置)
    slit1_center_x = -slit_distance / 2              # 中心のx座標
    slit1_outer_x  = slit1_center_x - slit_width / 2 # スリットの外側のx座標
    slit1_inner_x  = slit1_center_x + slit_width / 2 # スリットの内側のx座標
    slit1_top_y    = slit_height / 2                 # 一番上のy座標
    slit1_bottom_y = -slit_height / 2                # 一番下のy座標

    # 二つ目のスリット(x座標がプラスになる位置に設置)
    slit2_center_x = slit_distance / 2               # 中心のx座標
    slit2_outer_x  = slit2_center_x + slit_width / 2 # スリットの外側のx座標
    slit2_inner_x  = slit2_center_x - slit_width / 2 # スリットの内側のx座標
    slit2_top_y    = slit_height / 2                 # 一番上のy座標
    slit2_bottom_y = -slit_height / 2                # 一番下のy座標

    # 二重スリット生成
    slit1_area_judge = ((slit1_outer_x <= xx) 
        & (xx <= slit1_inner_x) 
        & (slit1_bottom_y <= yy) 
        & (yy <= slit1_top_y))
    slit2_area_judge = ((slit2_inner_x <= xx)
        & (xx <= slit2_outer_x)
        & (slit2_bottom_y <= yy)
        & (yy <= slit2_top_y))
    double_slit_mask = np.where(slit1_area_judge | slit2_area_judge, 1, 0)

    return double_slit_mask

# 光の伝搬とその強度の計算
def cal_intensity(mask: np.ndarray) -> np.ndarray:
    result = fft.fftshift(fft.fft2(fft.fftshift(mask))) # フラウンホーファー回折
    intensity = np.abs(result)**2 # シミュレーション結果の強度
    intensity = intensity / np.amax(intensity) # 強度正規化
    return intensity

# sinc関数
def sinc(x :np.ndarray) -> np.ndarray:
    return np.sin(np.pi * x) / (np.pi * x)

# シミュレーション（伝搬＆強度計算）
double_slit_mask = generate_double_slit_mask()
intensity = cal_intensity(double_slit_mask)

# 解析解計算
x_max_diffraction = wavelength * prop_distance / (pixel_width * 2)
x_diffraction = np.linspace(-x_max_diffraction, x_max_diffraction, len(x))
y_diffraction = x_diffraction
xx_diffraction, yy_diffraction = np.meshgrid(x_diffraction, y_diffraction)
xx_spatial_freq = xx_diffraction / (wavelength * prop_distance)
yy_spatial_freq = yy_diffraction / (wavelength * prop_distance)
analytical_prop = 2 * slit_width * slit_height * np.cos(np.pi * slit_distance * xx_spatial_freq) \
      * sinc(slit_width * xx_spatial_freq) * sinc(slit_height * yy_spatial_freq) # 解析解
intensity_analytical = np.abs(analytical_prop)**2 # 解析解の強度
intensity_analytical = intensity_analytical / np.amax(intensity_analytical) # 強度正規化
extent_diffraction   = [x_diffraction.min(), x_diffraction.max(), y_diffraction.min(), y_diffraction.max()]

# 二重スリット生成確認
plt.subplots()
plt.imshow(double_slit_mask, cmap='binary_r'
           ,extent=[x.min(), x.max(), y.min(), y.max()])
plt.xlabel('x [mm]') 
plt.ylabel('y [mm]') 

# スクリーンに映る強度像確認
## シミュレーション強度像参照
plt.subplots()
plt.imshow(intensity, cmap='binary_r'
            ,extent=extent_diffraction)
plt.xlabel('x [mm]') 
plt.ylabel('y [mm]')
plt.title('simulation result')
plt.colorbar(label='Intensity [a.u.]')

## 解析解強度像参照
plt.subplots()
plt.imshow(intensity_analytical, cmap='binary_r'
            ,extent=extent_diffraction)
plt.xlabel('x [mm]') 
plt.ylabel('y [mm]')
plt.title('analytical result')
plt.colorbar(label='Intensity [a.u.]')

indeces = np.where((-space_size_expand / 2 < x_diffraction) & (x_diffraction < space_size_expand / 2))[0]
min_index = indeces[0]
max_index = indeces[-1]
intensity_expand = intensity[min_index:max_index, min_index:max_index]
intensity_analytical_expand = intensity_analytical[min_index:max_index, min_index:max_index]

## シミュレーション（拡大）
min_val = x_diffraction[min_index]
max_val = x_diffraction[max_index]
extent_diffraction = [min_val, max_val, min_val, max_val]
plt.subplots()
plt.imshow(intensity_expand, cmap='binary_r'
            ,extent=extent_diffraction)
plt.xlabel('x [mm]') 
plt.ylabel('y [mm]')
plt.title('simulation result')
plt.colorbar(label='Intensity [a.u.]')

## 解析解（拡大）
plt.subplots()
plt.imshow(intensity_analytical_expand, cmap='binary_r'
            ,extent=extent_diffraction)
plt.xlabel('x [mm]') 
plt.ylabel('y [mm]')
plt.title('analytical result')
plt.colorbar(label='Intensity [a.u.]')

plt.show()

脚注

1. 単一の周波数のみを持つならば、波長も一つに決まるのでこの光は単色光と呼ばれます。

2. 大きさと言っていますが$u(\vec{r})$は複素数であることに注意してください。

3. 具体的にどの程度二重スリットとスクリーンが離れているか考えたくなると思います。これに関しては数メートル程度ととらえれば良いです。どこかの星と地球くらい離れている必要はありません。

4. $\text{sinc}(x)=\sin x/x$を定義とする場合もあります。

5. エイリアシングについてはこの記事で紹介しました。https://zenn.dev/torataro/articles/2023-06-08-discrete_fourier_transform