はじめに
以前こんな記事を書きました。
https://zenn.dev/torataro/articles/2023-02-26-fourier_transform
これはがっつり数学の話でプログラミングという観点では実用的ではないです。今回はコンピュータ内でフーリエ変換を実現する離散フーリエ変換について紹介していきます。上記記事の内容は本記事でもフォローしていくつもりですので、上記記事を読む必要はありません。
離散フーリエ変換って?
初めに次のデータ列を考えてみます。
\mathbf{f}=(f_{0}\;f_{1}\;\cdots\;f_{N-2}\;f_{N-1})^{\top}
これはベクトル\mathbf{f}の定義で、その要素としてf_{n},n\in\mathbb{Z}_{\geq 0}が格納されています。全要素数はNです。要素f_{n}自体がnのみに依存する関数なので、このベクトルは一次元の信号と呼ばれ、例として音声信号や株価情報などが挙げられます。このベクトルの要素に対する次の処理が離散フーリエ変換になります。
\begin{align*}
F_{m}&=\sum_{n=0}^{N-1}f_{n}\exp\left(-i2\pi\frac{nm}{N}\right)\\
f_{n}&=\frac{1}{N}\sum_{m=0}^{N-1}F_{m}\exp\left(i2\pi\frac{nm}{N}\right)
\end{align*}
前者が離散フーリエ変換、後者はその逆変換で逆離散フーリエ変換と呼びます。当然、変換&逆変換と読んでいるくらいなので行ったり来たりできる関係にありますが、なぜ可能なのでしょうか?線形代数の知識を使って説明します。
離散フーリエ変換の原理
内積と一次結合
次のベクトル\bm{a},\bm{b}について
\bm{a}=(a_{0}\;a_{1}\;a_{2})^{\top},\;\bm{b}=(b_{0}\;b_{1}\;b_{2})^{\top}
ベクトル\bm{a},\bm{b}の要素は複素数であるとします。ここで標準基底
\bm{e}_{0}=(1\;0\;0)^{\top},\;\bm{e}_{1}=(0\;1\;0)^{\top},\;\bm{e}_{2}=(0\;0\;1)^{\top}
を使うと\bm{a}は、
\bm{a}=a_{0}\bm{e}_{0}+a_{1}\bm{e}_{1}+a_{2}\bm{e}_{2}
と書けます。このような足し合わせを一次結合といいます。このとき内積\langle \bm{a},\bm{b}\rangleは次で定義されます。
\langle \bm{a},\bm{b}\rangle=\sum_{n=0}^{3-1}a_{n}b_{n}^{*}
特徴的なのは\bm{b}の要素に複素共役がかかっていることです。そうすれば\langle \bm{a},\bm{a}\rangleと同じベクトル同士の内積を計算したときベクトルの大きさが得られます。もし\bm{a},\bm{b}がN個を要素に持つベクトルならば、その内積は
\langle \bm{a},\bm{b}\rangle=\sum_{n=0}^{N-1}a_{n}b_{n}^{*}
とそのまま拡張した形になります。話を戻します。ベクトル\bm{a}と標準基底\bm{e}_{0}との内積を取ると、
\langle \bm{a},\bm{e}_{0}\rangle=a_{0}\cdot 1 + a_{1}\cdot 0 + a_{2}\cdot 0 = a_{0}
基底の係数a_{0}が抽出できます。つまり標準基底は自身の係数を抽出する抽出特性を有しているということです。なぜ抽出できるかというと、基底同士の内積を次のように計算したとき
\langle \bm{e}_{n},\bm{e}_{m}\rangle=
\left\{
\begin{array}{ll}
1 & n=m \\
0 & n\ne m
\end{array}
\right.
同じ基底ならば1を、異なる基底ならば0を取るからです。これを直交性といいます。直交性について同じ基底のとき、内積の計算結果が必ずしも1を取る必要はなく、0以外の数値であればよいです。ただ異なる基底で必ず0を取る必要があります。0以外の数値を取るならば、異なる基底の係数も抽出されてしまいます。
最後に、さきほどの内積の結果を使えば次の一次結合でベクトル\bm{a}が再度表現できます。
\bm{a}=\langle \bm{a},\bm{e}_{0}\rangle\bm{e}_{0}
+\langle \bm{a},\bm{e}_{1}\rangle\bm{e}_{1}
+\langle \bm{a},\bm{e}_{2}\rangle\bm{e}_{2}
とにかく重要なのは抽出特性と内積による線形結合です。この二つの性質が離散フーリエ変換と逆変換を成り立たせています。それを次に紹介します。
逆離散フーリエ変換と新たな基底
先ほど標準基底が直交性を有することによる抽出特性と、標準基底との内積で元のベクトルが再構築できたのを確認しました。このような基底はほかにもあり、その例として次のベクトルを紹介します。
\mathbf{e}_{m}=\left(
\exp\left(i2\pi\frac{0\cdot m}{N}\right)\;
\exp\left(i2\pi\frac{1\cdot m}{N}\right)\;
\cdots\;
\exp\left(i2\pi\frac{(N-1)\cdot m}{N}\right)
\right)^{\top}
ここでm\in\mathbb{Z}_{\geq 0}です。このベクトルに対して次のような線形結合を考えます。
\mathbf{f}=\frac{1}{N}\sum_{m=0}^{N-1}F_{m}\mathbf{e}_{m}
このベクトル\mathbf{f}のとある要素f_{n}を参照すると、
f_{n}=\frac{1}{N}\sum_{m=0}^{N-1}F_{m}\exp\left(i2\pi\frac{nm}{N}\right)
まぎれもなく逆離散フーリエ変換になります。これが逆変換の正体です。そして標準基底の係数が抽出できたのと同じように各基底の係数F_{m}をこの基底でも抽出できるでしょうか?それを次に示します。
抽出特性と離散フーリエ変換
基底が抽出特性を満たすには直交性を持っていなければなりませんでした。それを確認するために、内積\langle \mathbf{e}_{m},\mathbf{e}_{m'}\rangleを計算します。ここでm'\in\mathbb{Z}_{\geq 0}です。
\langle \mathbf{e}_{m},\mathbf{e}_{m'}\rangle=
\sum_{n=0}^{N-1}\exp\left(i2\pi\frac{nm}{N}\right)\exp\left(-i2\pi\frac{nm'}{N}\right)
=\sum_{n=0}^{N-1}\exp\left(i2\pi\frac{n(m-m')}{N}\right)
よりm-m'=0から
\exp\left(i2\pi \frac{n(m-m')}{N}\right)=1
なので、
\langle \mathbf{e}_{m},\mathbf{e}_{m'}\rangle=\sum_{n=0}^{N-1}1=N
です。
\langle \mathbf{e}_{m},\mathbf{e}_{m'}\rangle=
\sum_{n=0}^{N-1}\exp\left(i2\pi\frac{nm}{N}\right)\exp\left(-i2\pi\frac{nm'}{N}\right)
=\sum_{n=0}^{N-1}\exp\left(i2\pi\frac{n(m-m')}{N}\right)
この式展開までは同じ。ここでk=m-m'と置いてしまいましょう。そうすると、
\langle \mathbf{e}_{m},\mathbf{e}_{m'}\rangle
=\sum_{n=0}^{N-1}\exp\left(i2\pi\frac{nk}{N}\right)
=\sum_{n=0}^{N-1}\exp\left(i2\pi\frac{k}{N}\right)^{n}
という公比\exp\left(i2\pi k/N\right)の総和になるので、等比数列の和の公式から、
\langle \mathbf{e}_{m},\mathbf{e}_{m'}\rangle=\frac{\displaystyle\exp\left(i2\pi k\right)-1}{\exp\left(\displaystyle i2\pi \frac{k}{N}\right)-1}
となります。ここでm,m'\in\mathbb{Z}_{\geq 0}であることを思い出すと、k=m-m'\in\mathbb{Z}なので、
\exp\left(i2\pi k\right)=1
より、
\langle \mathbf{e}_{m},\mathbf{e}_{m'}\rangle=0
です。
これらの結果をまとめると、次のように直交性を記述できます。
\langle \mathbf{e}_{m},\mathbf{e}_{m'}\rangle=
\left\{
\begin{array}{ll}
N & n=m \\
0 & n\ne m
\end{array}
\right.
よって次の内積
\langle \mathbf{f},\mathbf{e}_{m'}\rangle=\sum_{n=0}^{N-1}f_{n}\exp\left(-i2\pi\frac{nm}{N}\right)=F_{m}
は係数F_{m}を抽出します。これが離散フーリエ変換です。
信号処理の観点から
フーリエ級数展開が教えてくれるのは、任意の信号f(t)がいろんな周波数の正弦波の足し合わせで表されるということです。式で記述すると信号f(t)は次のようになります。
f(t)=\sum_{n=-\infty}^{\infty}A_{n}\cos(2\pi\nu_{n}t + \theta_{n})
正弦波として\sinを思い浮かべる人もいると思いますが、\sinも\cosも区別せずに両方とも正弦波と呼びます。それよりもA_{n}を解析することで信号f(t)が周波数\nu_{n}の正弦波をどれだけ含むかが分かること、\theta_{n}を解析することで正弦波がどれだけずれているか分かることのほうがが重要です。それを知るための手段がフーリエ変換です。
フーリエ変換と逆フーリエ変換
フーリエ変換と逆フーリエ変換は次の定義です。
\begin{align*}
F(\nu)&=\int_{-\infty}^{\infty} f(t)\exp(-i2\pi \nu t)dt\\
f(t)&=\int_{-\infty}^{\infty} F(\nu)\exp(i2\pi \nu t)d\nu
\end{align*}
前者がフーリエ変換、後者が逆フーリエ変換です。特にf(t),F(\nu)のフーリエ変換、逆変換は
\mathcal{F}[f(t)]=F(\nu),\;\mathcal{F}^{-1}[F(\nu)]=f(t),
と書かれることが多いです。フーリエ変換を使えば、時間領域tに存在するf(t)を周波数領域\nuにマッピングし、時間とは異なる観点から情報を捉えられるようになります。このF(\nu)を調べることで次の情報が得られます。\text{Arg}は複素数の偏角です。
| \lvert F(\nu)\rvert |
\text{Arg}(F(\nu)) |
| 正弦波の振幅を反映。信号f(t)が周波数\nuの正弦波をどれだけ含んでいるか分かる。 |
正弦波の初期位相を反映。周波数\nuの正弦波の山の位置が分かる。 |
振幅、初期位相は次の正弦波のA,\theta_{0}に該当します。
A\cos(2\pi\nu t + \theta_{0})
ここで逆フーリエ変換の積分対象であるF(\nu)\exp(i2\pi \nu t)は、\theta(\nu)=\text{Arg}(F(\nu))と置けば、
F(\nu)\exp(i2\pi \nu t)=\lvert F(\nu)\rvert e^{i\theta(\nu)}\exp(i2\pi \nu t)=\lvert F(\nu)\rvert\exp\left[i(2\pi \nu t + \theta(\nu))\right]
\expの中身が\cosに一致することが分かります。実際\exp(i2\pi \nu t)は複素正弦波と呼ばれ、逆フーリエ変換自体も信号f(t)の(複素)正弦波の足し合わせを表しているのです。厳密な比較ではありませんが、上記から\lvert F(\nu)\rvertはA、\text{Arg}(F(\nu))は\theta_{0}に対応していることが感じ取れるはずです。
離散フーリエ変換では時間領域の信号はf_{n}、それを周波数領域にマッピングした結果はF_{m}になります。フーリエ変換を離散化することでそれぞれを比較しましょう。
デルタ関数と標本化
先にデルタ関数を紹介します。デルタ関数\delta(t)は次の定義です。
\begin{align*}
\int_{-\infty}^{\infty} f(t)\delta(t-t')dt&=\int_{-\infty}^{\infty} f(t)\delta(t'-t)dt=f(t') \\
&\int_{-\infty}^{\infty} \delta(t)dt=1
\end{align*}
デルタ関数は何か実態があるわけでなくこの二式で定義されます。前者がデルタ関数の抽出特性を表しています。とある時間t=t'での関数fの値f(t')を抽出しています。後者の式はデルタ関数が1で正規化されることを表しています。ただこの定義だとイメージが湧きにくいので次のように書かれることもあります。
\delta(t)=
\left\{
\begin{array}{ll}
\infty & t=0 \\
0 & t\ne 0
\end{array}
\right.
これはインパルス信号と呼ばれるもので、もし図化するならば次のようになります。
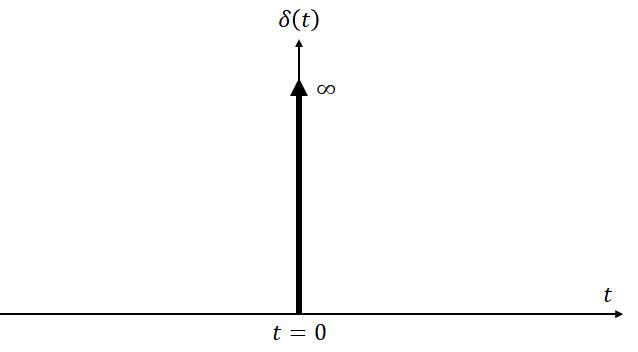
続いて標本化です。音などを考えると信号は連続であることが多いです。そしてこの信号をメモリに格納することを考えれば、この連続な信号から値を選ぶ必要がでてきます。その操作が標本化です。サンプリングとも言われます。標本化として次の図のような方法が一般的でしょう。

この標本化では、とある間隔\Delta tで信号を選んでいます。選ばれた信号は次のようにベクトルで格納することができます。
\mathbf{f}=(\cdots\;f(-2\Delta t)\;f(-\Delta t)\;f(0)\;f(\Delta t)\;f(2\Delta t)\;\cdots)^{\top}
この選ばれた信号に対して後々積分ができるように次の列を考えます。
s_{\Delta t}(t)=\sum_{n=-\infty}^{\infty}\delta(t-n\Delta t)
これを図化すると次のようになります。
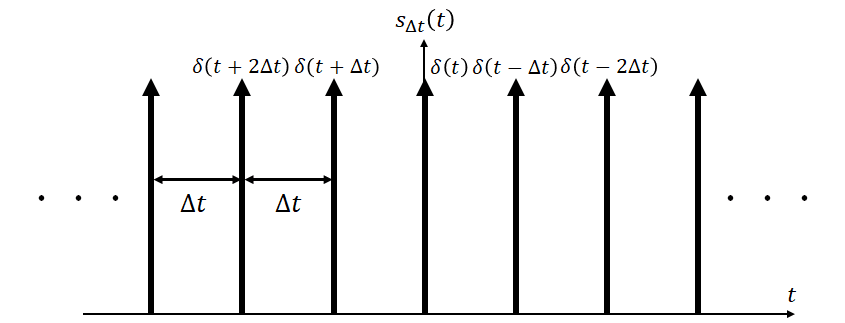
選んだ場所でデルタ関数の角が立っていることが確認できます。これはくし型関数と呼ばれるものです。くし型関数使えば
f_{s}(t)=f(t)s_{\Delta t}(t)=\sum_{n=-\infty}^{\infty}f(n\Delta t)\delta(t-n\Delta t)
のように標本化したものを積分できるようになります。そしてこのくし型関数ですが\Delta tを一周期とする周期関数なので複素フーリエ級数展開(Appendix参照)を使って次の様に記述することもできます。
s_{\Delta t}(t)=\frac{1}{\Delta t}\sum_{n=-\infty}^{\infty}\exp\left(i2\pi\frac{nt}{\Delta t}\right)
この式は後で使います。
フーリエ変換の離散化
f(t)のフーリエ変換がF(\nu)であるならば、標本化後のフーリエ変換はどうなるでしょうか?f_{s}(t)をフーリエ変換することで調べましょう。その前に畳み込み積分と積のフーリエ変換の公式を紹介します。畳み込み積分は二つの関数f=f(t),g=g(t)を用いて次式で定義されます。
(f*g)(t)=\int_{-\infty}^{\infty}f(\tau)g(t-\tau)d\tau
ここで*は畳み込み積分を示す演算子として定義します。また関数の積f(t)g(t)のフーリエ変換はf(t),g(t)のフーリエ変換をF=F(\nu),G=G(\nu)と置けば、
\mathcal{F}[f(t)g(t)]=(F*G)(\nu)=\int_{-\infty}^{\infty}F(\nu')G(\nu-\nu')d\nu'
と変換結果の畳み込み積分で表されます(証明はAppendix参照)。f_{s}(t)=f(t)s_{\Delta t}(t)のフーリエ変換をF_{s}(\nu)と置き、上記結果を使えば、
F_{s}(\nu)=(F*S_{\Delta t})(\nu)=\int_{-\infty}^{\infty}F(\nu')S_{\Delta t}(\nu-\nu')d\nu'
となります。S_{\Delta t}=S_{\Delta t}(\nu)はくし型関数s_{\Delta t}(t)のフーリエ変換で次のような形になります。
\begin{align*}
S_{\Delta t}(\nu)=\mathcal{F}[s_{\Delta t}(t)]&=\int_{-\infty}^{\infty}\sum_{n=-\infty}^{\infty}\delta(t-n\Delta t)\exp(-i2\pi \nu t)dt \\
&=\sum_{n=-\infty}^{\infty}\int_{-\infty}^{\infty}\delta(t-n\Delta t)\exp(-i2\pi \nu t)dt\\
&=\sum_{n=-\infty}^{\infty}\exp(-i2\pi \nu n\Delta t)
\end{align*}
ここで上から三行目のイコールの時点でデルタ関数の抽出特性を使いました。この結果とくし型関数の複素フーリエ級数展開の結果を比較すると、
S_{\Delta t}(\nu)=\frac{1}{\Delta t}s_{\frac{1}{\Delta t}}(\nu)=\frac{1}{\Delta t}\sum_{n=-\infty}^{\infty}\delta\left(\nu-\frac{n}{\Delta t}\right)
と最終的にくし型関数になることが分かります。この結果からデルタ関数の抽出特性を使えば
\begin{align*}
F_{s}(\nu)&=\int_{-\infty}^{\infty}F(\nu')\frac{1}{\Delta t}\sum_{n=-\infty}^{\infty}\delta\left(\nu-\nu'-\frac{n}{\Delta t}\right)d\nu'\\
&=\frac{1}{\Delta t}\sum_{n=-\infty}^{\infty}\int_{-\infty}^{\infty}F(\nu')\delta\left(\left(\nu-\frac{n}{\Delta t}\right)-\nu'\right)d\nu'\\
&=\frac{1}{\Delta t}\sum_{n=-\infty}^{\infty}F\left(\nu-\frac{n}{\Delta t}\right)
\end{align*}
となります。数式をもとにF_{s}(\nu)を描くと次のようなイメージです。
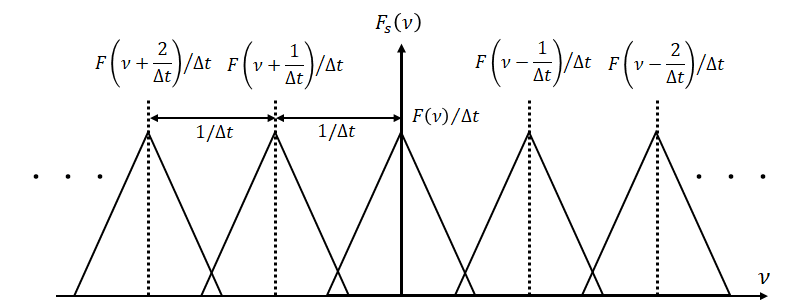
F(\nu)が一つの山を成し、\nu_{s}=1/\Delta tの周期で山の頂点が現れることが確認できます。\nu_{s}はサンプリング周波数といい、1秒間に何回サンプリングするか決めるものです。当然沢山サンプリングすると山と山の間隔は離れます。この話は次の標本化定理の紹介で行います。
離散フーリエ変換の話に戻りましょう。実際\Delta tで標本化したならば、コンピュータ上で格納できる最大周波数は\nu_{s}になります。また離散フーリエ変換した結果F_{m}は、変換対象のデータ数と同じN個得られるので、フーリエ変換後の結果を離散化するならば次の方法になります。
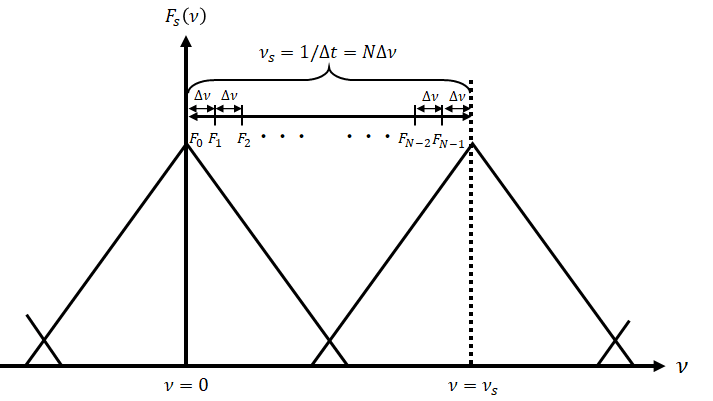
つまり周波数領域で離散化するというのは、山の頂点から次の山の頂点の間でN個値を取ってくることに他ならないわけです。この離散化の間隔を\Delta \nuと置けば次の式が成り立ちます。
\Delta t\Delta \nu = \frac{1}{N}
量子力学の不確定性原理のような数式ですね。この式から\Delta tと\Delta \nuの大きさはトレードオフの関係にあることが分かります。周波数領域でも一定の精度を担保したいならばデータを増やすしかないということです。
標本化定理とエイリアシング
標本化後の信号のフーリエ変換F_{s}(\nu)より、本来得たい信号の結果F(\nu)が繰り返し現れることが確認できました。そうすると懸念されるのはF(\nu)同士が重ね合わさるところです。図示すると灰色の個所になります。
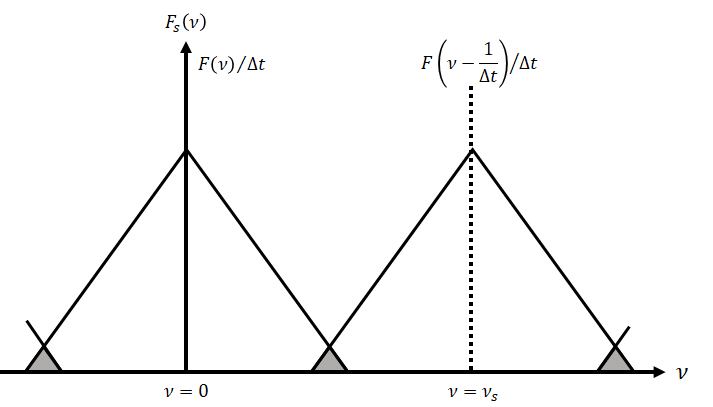
この重ね合わさった部分の周波数領域はF(\nu)が取る本来の値とは異なるため、そのまま逆フーリエ変換をすると正しい信号f(t)を再現できなくなります。これをエイリアシングといいます。
もし信号f(t)が最大周波数\nu_{\text{max}}までの正弦波の重ね合わせで構成されているならば、逆フーリエ変換で信号f(t)を回復するために次式を満たしている必要があります。
\nu_{s}\geq 2\nu_\text{max}
これは標本化定理と呼ばれるもので、F(\nu)が重ね合わさらない条件になります。信号処理論で最も重要な式といってもよいかもしれません。標本化定理を満たしているとき次のようなイメージになります。

エイリアシングを起こさない条件が明確になりましたが、エイリアシングってどんな状態を表すのでしょうか?\nu_{\text{max}}の周波数を持つ正弦波でもって説明します。まず正弦波の中から青点で沢山サンプリングします。

上図が正弦波をサンプリングした結果です。当然、この時サンプリングした点と点同士をつなぐとしっかりとオレンジの正弦波に追随していることが分かります。この点を極限まで減らした時、それでも正弦波を再現できるサンプリング数はいくつでしょうか?結論次の図の通りです。

このとき正弦波の山の頂上と谷の底でサンプリングを行いました。これらの点と点をつなぐと正弦波というよりは三角波になりますが、それでも正弦波の振動を表現することができています。実際、標本化定理は最大周波数を持つ正弦波の一回の振動で二回以上サンプリングすれば、元の信号を復元することができると主張しています。二回でのサンプリング結果が上の図です。
ではエイリアシングの場合どうなるでしょうか?それが次の図です。

エイリアシングは正弦波の振動をとらえきれない(サンプリング数が足りていない)ことで発生する現象になります。このとき点と点をつなぐと\nu_{s}-\nu_{\text{max}}の低周波数に折り返した正弦波が出現します。ゆえにエイリアシングは折り返し雑音とも呼ばれます。
最後に
離散フーリエ変換は初めにも紹介した通り、コンピュータ上で計算できるフーリエ変換になります。ただ離散フーリエ変換がフーリエ変換から導かれるというよりは、離散フーリエ変換が本来のフーリエ変換と共通する性質(推移則など)を持っているため、コンピュータ上での周波数領域へのマッピング方法として離散フーリエ変換が採用されていると捉えるほうがよいでしょう。
離散フーリエ変換を行列化すると、ユニタリ行列が現れたりともっと面白い性質があるのですが、長くなりそうなのでここらで終わりにします。最後まで読んでいただきありがとうございました!
Appendix
複素フーリエ級数展開
複素フーリエ級数展開の定義は次の通りである。
\begin{align*}
f(t)&=\sum_{n=-\infty}^{\infty}c_{n}\exp\left(i2\pi\frac{nt}{T}\right)\\
c_{n}&=\frac{1}{T}\int_{-T / 2}^{T / 2}f(t)\exp\left(-i2\pi\frac{nt}{T}\right)dt
\end{align*}
ただし複素フーリエ級数展開を満たすものはf(t)=f(t+T)の周期関数である。くし型関数の時T=\Delta tであり、c_{n}=1/\Delta tとなる。
\mathcal{F}[f(t)g(t)]=(F*G)(\nu)の証明
(F*G)(\nu)の逆フーリエ変換がf(t)g(t)になることを証明する。
\begin{align*}
\mathcal{F}^{-1}[(F*G)(\nu)]&=\int_{-\infty}^{\infty}\left(\int_{-\infty}^{\infty}F(\nu')G(\nu-\nu')d\nu'\right)\exp\left(i2\pi\nu t\right)d\nu\\
&=\int_{-\infty}^{\infty}F(\nu')\left(\int_{-\infty}^{\infty}G(\nu-\nu')\exp\left(i2\pi\nu t\right)d\nu\right)d\nu'\\
\end{align*}
ここでs=\nu-\nu'と置けば、\nu=s+\nu'なので
\begin{align*}
\mathcal{F}^{-1}[(F*G)(\nu)]&=\int_{-\infty}^{\infty}F(\nu')\left(\int_{-\infty}^{\infty}G(s)\exp\left(i2\pi(s+\nu') t\right)ds\right)d\nu'\\
&=\left(\int_{-\infty}^{\infty}F(\nu')\exp\left(i2\pi \nu' t\right)d\nu'\right)
\left(\int_{-\infty}^{\infty}G(s)\exp\left(i2\pi s t\right)ds\right)\\
&=\mathcal{F}^{-1}[F(\nu')]\mathcal{F}^{-1}[G(s)]=f(t)g(t)
\end{align*}
よって
\mathcal{F}[f(t)g(t)]=(F*G)(\nu)
である。■
余談であるが
\mathcal{F}[(f*g)(t)]=F(\nu)G(\nu)
も成り立つ。証明の仕方は変わらない。(むしろこっちのほうがよく取り上げられる。)
参考文献
和田 成夫(著)「よくわかる信号処理」森北出版株式会社
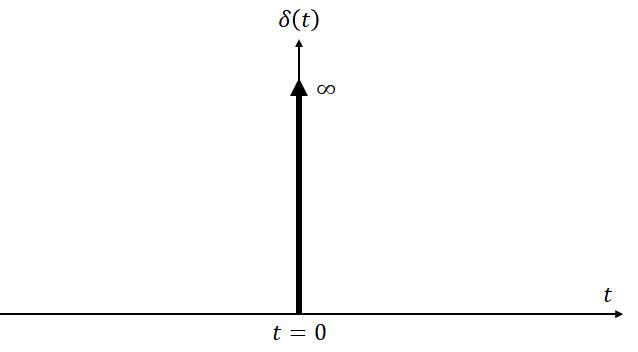

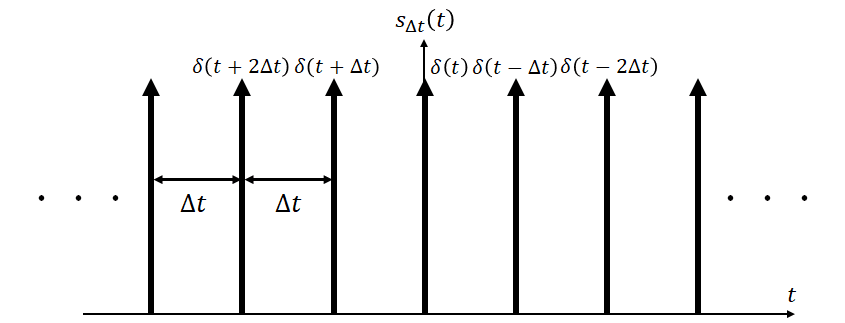







Discussion