逆フーリエ変換でなぜフーリエ変換前の関数に戻せるのか？

結論

A: それは逆変換だからです？

そんなワケありません。それはメロスが走っているのは走れメロスだからと言っているようなものです。ただ大学などの研究でフーリエ変換にお世話になっている人でも逆変換だからと割り切って使っている人が一定数います。本記事ではタイトルに対する結論を

A: 逆フーリエ変換は複素正弦波の一次結合を取る操作だから。

と置きます。一次結合は線形結合とも言いますね。フーリエ変換は解析学などで勉強することが多いようですが、本記事では線形代数の視点で展開して行きます。なのでベクトルの計算はある程度知っているけど、フーリエ変換はよく理解してなかったという方に対して理解を促すような記事になっています。ぜひお楽しみください。

ベクトルの計算のほかに以下の前提で本記事は展開します。
・$i$は虚数単位$i=\sqrt{-1}$とする。
・オイラーの公式$e^{i\theta}=\cos{\theta}+i\sin{\theta}$は知っている。
・加えて$e^{i\theta}=\exp(i\theta)$という記述方法もあることも知っている。
・複素数全体を$\mathbb{C}$と置き、$z$は複素数であることを$z\in\mathbb{C}$と書く。
・$z$の複素共役を$z^{*}$で定義する。

内積と一次結合

まず線形代数の話をします。準備のために二つのベクトルを定義しましょう。

$$\bm{a}=\begin{pmatrix}a_{1} \\ a_{2} \\ a_{3} \end{pmatrix},\; \bm{b}=\begin{pmatrix}b_{1} \\ b_{2} \\ b_{3} \end{pmatrix}$$

さらに$\bm{a},\bm{b}$の要素を

$$a_{1},a_{2},a_{3},b_{1},b_{2},b_{3}\in\mathbb{C}$$

とします。このときベクトル$\bm{a},\bm{b}$は複素数を要素に持つベクトルで、これは複素ベクトルといいます。またベクトルには基底というものがあり、特に良い性質を持つものとして直交基底があります。直交基底は異なる基底を一切含まない混じりけのないようなもので例えば、

$$\bm{e}_{1}=\begin{pmatrix}1 \\ 0 \\ 0 \end{pmatrix},\; \bm{e}_{2}=\begin{pmatrix}0 \\ 1 \\ 0 \end{pmatrix},\; \bm{e}_{3}=\begin{pmatrix}0 \\ 0 \\ 1 \end{pmatrix}$$

が挙げられます。これは標準基底と呼びます。これを使えば$\bm{a}$は

$$\bm{a}=a_{1}\bm{e}_{1}+a_{2}\bm{e}_{2}+a_{3}\bm{e}_{3}$$

で表現できます。このようにいくつかのベクトルに係数を掛け、足し合わせる操作を一次結合といいます。そして各標準基底にかかる係数$a_{n}$の値を変化させれば三つの要素を持つすべての複素ベクトルを表現できます。これは後で紹介する完全性の伏線です。

次に内積です。高校などで学ぶ内積は各ベクトルの要素の積の総和になりましたが複素ベクトル$\bm{a},\bm{b}$の内積は次のように定義されます。

$$\langle \bm{a},\bm{b}\rangle=\sum_{n=1}^{3}a_{n}b_{n}^{*}$$

ここで特徴的なのは片方のベクトルの要素に複素共役がかかっている点です。これはエルミート内積と呼びます^[1]。もちろん複素数は実数を含むのでそのまま実数を要素とするベクトルにも適用できます。先ほど直交基底は混じりけがないと言いました。これは基底同士の内積を取った時に、

$$\langle \bm{e}_{n},\bm{e}_{m}\rangle=\delta_{nm}= \left\{ \begin{array}{ll} 1 & n=m \\ 0 & n\ne m \end{array} \right.$$

と自分自身との内積しか値を持たないということ意味します。$n,m$は$1,2,3$を取ります。そして$\delta_{nm}$はクロネッカーのデルタと呼びます。試しに標準基底との内積を取ってみましょう。

$$\langle \bm{a},\bm{e}_{1}\rangle=a_{1}\cdot 1+a_{2}\cdot 0+a_{3}\cdot 0=a_{1}$$

つまり内積を取る操作は直交基底にかかる係数を抽出する操作であり、直交基底は抽出特性を有することが分かりました。もちろん$\bm{e}_{2},\bm{e}_{3}$との内積でも$a_{2},a_{3}$が抽出できるのは想像に難くないです。直交基底が少しでも他の基底を含んでいたらここまできれいに抽出できなかったでしょう。最終的にベクトル$\bm{a}$は、

$$\bm{a}=\langle \bm{a},\bm{e}_{1}\rangle\bm{e}_{1}+\langle \bm{a},\bm{e}_{2}\rangle\bm{e}_{2}+\langle \bm{a},\bm{e}_{3}\rangle\bm{e}_{3}$$

と書けます。なんだか煩わしい書き方ですが、実はフーリエ変換して逆変換をする一連の流れはこの内積を計算し一次結合を取る操作に他ならないのです。

関数の内積とフーリエ変換

これまでのベクトルの話はなんだか当たり前に聞こえたかもしれません。しかしここから本番です。今一度フーリエ変換と逆フーリエ変換の定義を確認しましょう。$f(t)$は複素数を返却する複素関数$f(t)\in\mathbb{C}$とします。

$$\begin{align*} F(\nu)&=\int_{-\infty}^{\infty} f(t)\exp(-i2\pi \nu t)dt\in\mathbb{C} \\ f(t)&=\int_{-\infty}^{\infty} F(\nu)\exp(i2\pi \nu t)d\nu \end{align*}$$

前者が関数$f(t)$のフーリエ変換、後者が逆フーリエ変換です^[2]。$t$は時間などの連続なもので一概に離散化するのはナンセンスですが、こうしてみるとあたかもベクトルのように見えます。

$$f=(\cdots f(t_{0}-2\Delta t)\;f(t_{0}-\Delta t)\;f(t_{0})\;f(t_{0}+\Delta t)\;f(t_{0}+2\Delta t)\;\cdots)^{\top}$$

そうすると関数というのは無限次元のベクトルだと思うことができます。ならばベクトルの時に紹介した内積の考え方がそのまま役立ちそうです。ここでもう一つ関数$g(t)\in\mathbb{C}$を用意すれば、二つの関数の内積はベクトルの考え方に基づいて

$$\langle f,g\rangle=\int_{-\infty}^{\infty} f(t)g^{*}(t)dt$$

で定義できます。ここで$g(t)$を

$$g(t)=\exp(i2\pi\nu t)$$

とすれば、

$$\langle f,g\rangle = \int_{-\infty}^{\infty} f(t)\exp(-i2\pi\nu t)dt=F(\nu)$$

フーリエ変換が導けました！

複素正弦波とデルタ関数

この$\exp(i2\pi\nu t)$は複素正弦波と呼び^[3]、フーリエ変換とは任意の関数と複素正弦波の内積だということが明確になりました。複素正弦波はオイラーの公式を参照してもらえれば分かりますが、

$$\exp(i2\pi\nu t)=\cos(2\pi\nu t)+i\sin(2\pi\nu t)$$

正弦波$\sin(2\pi\nu t)$と余弦波$\cos(2\pi\nu t)$を含みます。ただ$\sin,\cos$は区別せず両方とも正弦波と呼ぶことが多いです^[4]。また複素正弦波も単に正弦波と呼びます。ここで正弦波の理解を促すため$\cos(2\pi\nu t)$に着目しグラフで描画しましょう。

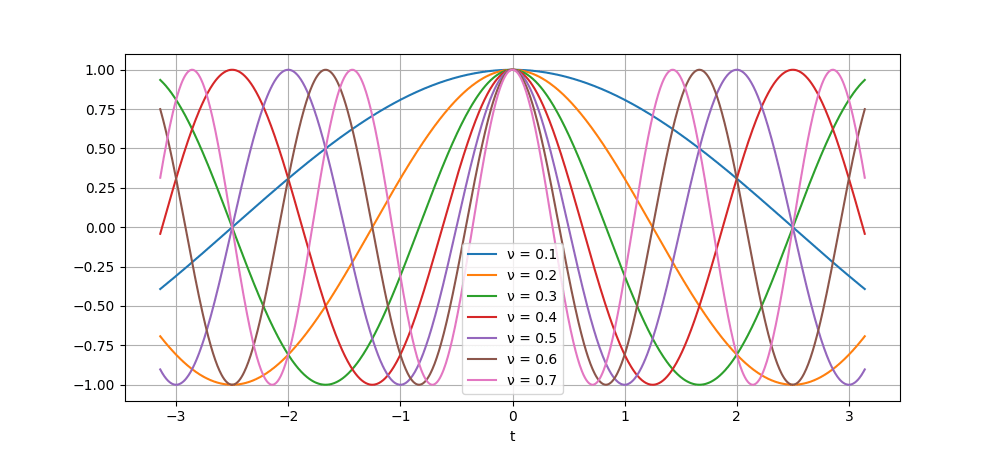
$\nu$の値を大きくすると山の頂点と隣の山の頂点の間隔が小さくなります。$t$が時間ならば$\nu$は周波数と呼び、単位時間あたりの振動数になります。さてこの複素正弦波ですがベクトルの直交基底に相当し、関数を記述するためのパーツとなります。これに伴って複素正弦波が直交基底同様の性質を持つことを示したいのですが準備が必要です。まずすべての周波数の複素正弦波を足し合わせます（積分します）。

$$\begin{align*} \int_{-\infty}^{\infty}\exp(i2\pi\nu t)d\nu &=\lim_{N \to \infty}\left[\frac{\exp(i2\pi\nu t)}{i2\pi t}\right]_{-N}^{N} \\ &=\lim_{N \to \infty}2N\frac{\sin(2\pi Nt)}{2\pi Nt}\\ &=\lim_{N \to \infty}2N\text{sinc}(2\pi Nt) \end{align*}$$

導出の際に$2i\sin(x)=e^{ix}-e^{-ix}$の関係を使いました。また$\text{sinc}(x)=\sin(x)/x$はsinc(ジンク、シンク)関数と呼び、$x\rightarrow 0$の極限で$1$を取ります。この積分結果は後々使うので

$$\tilde{\delta}_{N}(t)=2N\text{sinc}(2\pi Nt)$$

で定義しましょう。この積分結果を理解するために様々な$N$で設定した$\tilde{\delta}_{N}(t)$を見てみましょう。

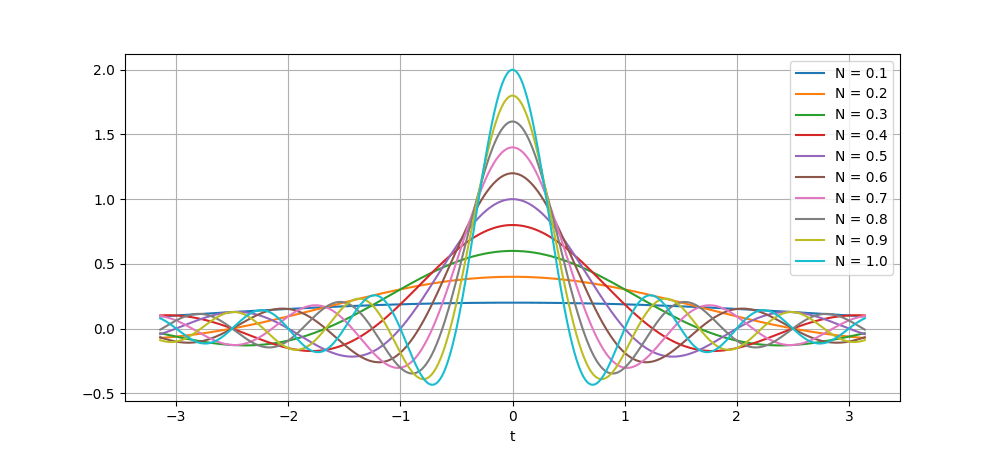
各$N$に対する$\tilde{\delta}_{N}(t)$の概形

$N$を大きくすればするほど$t=0$での値が大きくなり、それ以外は0に近づいていきます。これは先ほど描画した$\cos(2\pi\nu t)$のグラフを見てもらえばわかりますが、$t=0$で山の頂点がすべて一致し、それ以外ではずれています。なので重ね合わせたときに$t=0$で値が大きくなっていきそれ以外では山や谷の部分が打ち消しあっていきます^[5]。結局$\tilde{\delta}_{N}(t)$は

$$\lim_{N \to \infty}\tilde{\delta}_{N}(t)= \left\{ \begin{array}{ll} \infty & t=0 \\ 0 & t\ne 0 \end{array} \right.$$

と見なせます。この$t=0$で無限大の大きさを取るというのは物理や工学で重宝され、例えば音響学ではピストルの破裂音がこれに該当します。さらに$\tilde{\delta}_{N}(t)$は

$$\int_{-\infty}^{\infty} \tilde{\delta}_{N}(t)dt = 1$$

と全範囲の積分で$1$を取ります^[6]。さて話は変わってデルタ関数を紹介します。デルタ関数$\delta(t)$は次の定義です。

$$\begin{align*} \int_{-\infty}^{\infty} f(t)\delta(t-t')dt&=f(t') \\ \int_{-\infty}^{\infty} \delta(t)dt&=1 \end{align*}$$

デルタ関数は何か実態があるのではなくこの二つの積分で定義されます^[7]。前者の式はデルタ関数の抽出特性を表しています。関数$f(t)$の$t=t'$での値$f(t')$を抽出しています。$\delta(t-t')$でなくても$\delta(t'-t)$としても抽出結果は変わらないとします。後者はデルタ関数が全積分で正規化されていることを表しています。

さてこの正規化ですがなんだか$\tilde{\delta}_{N}(t)$に似ていませんか？どうやら$\tilde{\delta}_{N}(t)$は大きな$N$について次式を満たすようです。

$$\int_{-\infty}^{\infty} f(t)\tilde{\delta}_{N}(t-t')dt\approx f(t')$$

つまり$\tilde{\delta}_{N}(t)$もデルタ関数と同じ抽出特性を有するということが言えます。$N$を大きくすればするほどこの抽出性能が向上していきます。従ってデルタ関数の具体的な表現として、

$$\delta(t) = \lim_{N \to \infty}\tilde{\delta}_{N}(t)$$

と書かれることがあります^[8]。なので以後

$$\delta(t)=\int_{-\infty}^{\infty}\exp(i2\pi\nu t)d\nu$$

と置いてしまいましょう。ここまでで準備は終わりです。

複素正弦波は完全性と抽出特性を有する

さてフーリエ変換は複素正弦波と関数$f(t)$の内積でした。ここで便宜上、複素正弦波を

$$e_{\nu}(t)=\exp(i2\pi \nu t)$$

と置いておきます。この複素正弦波がベクトルの直交基底に相当するならば、フーリエ変換となる内積

$$F(\nu)=\langle f,e_{\nu}\rangle = \int_{-\infty}^{\infty} f(t)\exp(-i2\pi\nu t)dt$$

は複素正弦波の係数$F(\nu)$を抽出しているはずです。これは直交基底が各基底の係数を抽出していた時の議論から帰結する考察です。またこのときの一次結合は

$$f(t)=\int_{-\infty}^{\infty}\langle f,e_{\nu}\rangle e_{\nu}(t)d\nu=\int_{-\infty}^{\infty}F(\nu)\exp(i2\pi\nu t)d\nu$$

となるでしょう。周波数は連続なのでその一次結合は積分になります。これが逆フーリエ変換です。ついでに最初に紹介したベクトルもここに置いておきます。

$$\bm{a}=\langle \bm{a},\bm{e}_{1}\rangle\bm{e}_{1}+\langle \bm{a},\bm{e}_{2}\rangle\bm{e}_{2}+\langle \bm{a},\bm{e}_{3}\rangle\bm{e}_{3}$$

よく似ていると思いませんか？ベクトルの時は上の式のように基底$\bm{e}_{n}$の足し合わせでベクトルが表現できましたが、複素正弦波も同様でしょうか？ここではこの抽出特性と一次結合を確認しましょう。

フーリエ変換と抽出特性

まず$f(t)$は複素正弦波の一次結合で表されているという前提のもと、複素正弦波が抽出特性を持つことを示します。$\nu'$という周波数成分を抽出しましょう。

$$\begin{align*} \langle f,e_{\nu'}\rangle &= \int_{-\infty}^{\infty} f(t)\exp(-i2\pi\nu' t)dt\\ &=\int_{-\infty}^{\infty} \left(\int_{-\infty}^{\infty}F(\nu)\exp(i2\pi\nu t)d\nu\right)\exp(-i2\pi\nu' t)dt\\ &=\int_{-\infty}^{\infty} F(\nu)\left(\int_{-\infty}^{\infty}\exp(i2\pi\nu t)\exp(-i2\pi\nu' t)dt\right)d\nu\\ &=\int_{-\infty}^{\infty} F(\nu)\delta(\nu-\nu')d\nu = F(\nu') \end{align*}$$

こうして周波数$\nu'$を持つ複素正弦波の係数$F(\nu')$が抽出できました！これがフーリエ変換の仕組みです。

逆フーリエ変換と一次結合

先ほどの一次結合の計算を進めてみましょう。計算の都合上$t'$という変数も使います。

$$\begin{align*} \int_{-\infty}^{\infty}\langle f,e_{\nu}\rangle e_{\nu}(t)d\nu&=\int_{-\infty}^{\infty}\left(\int_{-\infty}^{\infty} f(t')\exp(-i2\pi\nu t')dt'\right)\exp(i2\pi\nu t)d\nu \\ &=\int_{-\infty}^{\infty}f(t')\left(\int_{-\infty}^{\infty}\exp(i2\pi\nu t)\exp(-i2\pi\nu t')d\nu\right)dt'\\ &=\int_{-\infty}^{\infty}f(t')\delta(t-t')dt'=f(t) \end{align*}$$

期待通り$f(t)$になることが確認できました！これは複素正弦波が完全性という性質を持つことに由来しています。完全性は係数を自由に変化させた関数を無限個足し合わせれば任意の関数が表現できる性質のことです。この関数が複素正弦波なわけです^[9]。

まとめ

さて長々と数式の展開だらけでしたが最初の結論をもう一度見てみましょう。

A: 逆フーリエ変換は複素正弦波の一次結合を取る操作だから。

この回答の裏に隠されている意図が、複素正弦波が完全性を有する点に由来しているということが伝わったでしょうか？またついでになりますが、フーリエ変換と逆フーリエ変換は行き来できる関係にあるのは、複素正弦波の抽出特性も関係していることも伝わったでしょうか？

本記事は線形代数の観点でフーリエ変換を論じました。実際、積分だらけでその感覚はなかったかもしれません。ただ逆フーリエ変換でどんな関数でも変換前の関数に戻せるかどうかは違和感を持つべきです。本当は関数$f(t)$はなめらかであるとか、無限の範囲の積分で発散しないことが求められます。これらを議論するのが解析学で大学では解析学などの講義で学ぶわけです。

脚注

1. $\langle \bm{a},\bm{b}\rangle=\sum_{n=1}^{3}a_{i}^{*}b_{i}$と$\bm{a}$の要素に複素共役がかかる形でも問題ないです。量子力学だとこっちが主流ですかね？

2. フーリエ変換にはいくつか流儀があります。例えば$\omega=2\pi\nu$とまとめてフーリエ変換の結果を$F(\omega)$とする場合があります。このときフーリエ変換または逆変換に$1/2\pi$分の係数をつける必要がありますが物理学ではこれはエネルギーや運動量の次元になるため、こちらのほうが都合がよかったりします。本記事で紹介した定義は音声画像処理をする際に適した定義になっていますね。

3. おそらく複素正弦波と呼ぶのは信号処理屋さん、電気回路屋さんくらいだと思います。ただ便利なのでこの名称を使わせてもらいます。

4. なぜなら$\sin,\cos$はカッコの中身（位相）が$\pi/2$ずれただけの違いなので区別する必要がないからです。

5. ちなみに$\sin(2\pi\nu t)$は$t=0$でそもそも$0$だし、$t\ne 0$で$\cos$同様打ち消しあうので無視で問題ないです。

6. $\int_{-\infty}^{\infty}\text{sinc}(x)dx=\pi$という結果を使いました。sinc関数の積分自体は複素積分を用いますが長くなるのでここでは割愛します。

7. デルタ関数は実は厳密な関数ではなく超関数と呼ばれるものです。一般的な関数はとある値（実数や複素数）に対してたった一つ値を返却しますが、超関数は抽出特性の通りとある関数$f$から値$f(t')$を返却するものなので、一概に関数と呼べないのです。

8. これは$\{\tilde{\delta_{N}}\}_{N\in\mathbb{R}}$という集合を考え、$N$が小さいほうから$\tilde{\delta_{N}}$を並べれば関数$\tilde{\delta_{N}}$の列ができます。デルタ関数はこの関数列の極限で表されていると言えます。

9. ほかにも完全性を持つ関数としてエルミート多項式、ルジャンドル多項式、ベッセル関数などがあります。