畳み込み積分と相関関数
まず畳み込み積分と相関関数の違いを見てみましょう。畳み込み積分f*gは次の定義です。
(f*g)(t)=\int_{-\infty}^{\infty}f(\tau)g(t-\tau)d\tau
相関関数R_{fg}は次の定義です。
R_{fg}(t)=\int_{-\infty}^{\infty}f(\tau)g(\tau-t)d\tau
これらの相違点は関数gの中身がt-\tauか\tau-tかだけです。しかしなぜはっきりと区別されるのでしょうか?それは式からとらえられる意味に大きな違いがあるからです。
畳み込み積分とは?
畳み込み積分は幅広い分野で登場し、とりわけ信号処理におけるフィルタや制御理論におけるシステムの応答の解析に使われます。t,\tauを時間の変数とみて、今一度畳み込み積分を参照すると、
(f*g)(t)=\int_{-\infty}^{\infty}f(\tau)g(t-\tau)d\tau
という定義であることは紹介しました。ここでg(t-\tau)に着目しましょう。gについて\tau_{1}<\tau_{2}<\tau_{3}を満たす、定数\tau=\tau_{1},\tau_{2},\tau_{3}を用意すると、g(t-\tau_{1}),g(t-\tau_{2}),g(t-\tau_{3})の関係は、
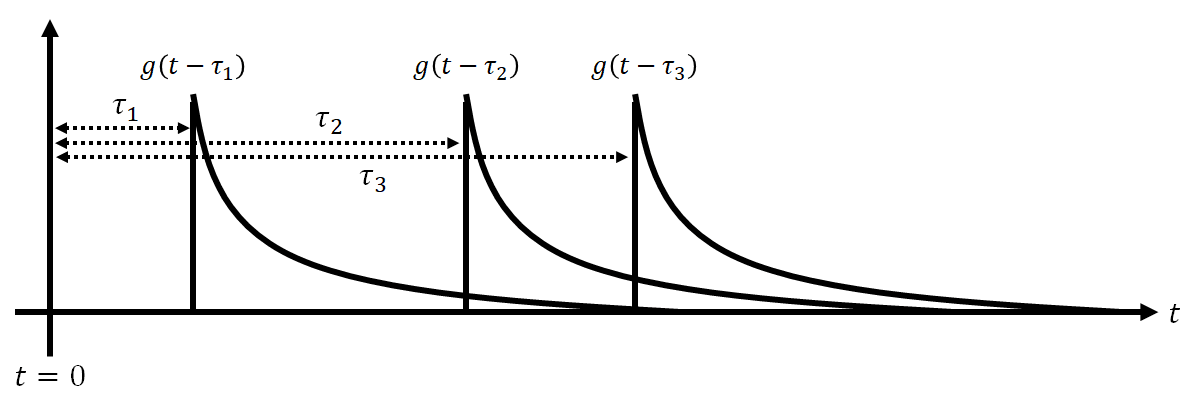
となります。つまり\tauという変数を大きくすればするほど、関数gは時間が経過する方向に進むため、\tauは関数gの時間遅れを表す変数だということがわかります。ここでさらにf(\tau_{1}),f(\tau_{2}),f(\tau_{3})をg(t-\tau_{1}),g(t-\tau_{2}),g(t-\tau_{3})に掛けましょう。こんな感じになります。
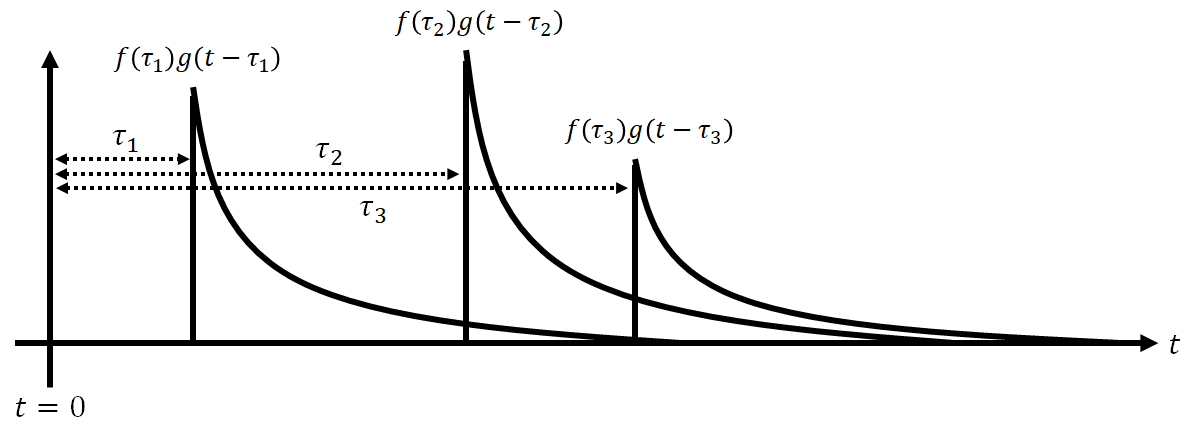
あとはこれらを足し合わせれば、
\sum_{i=1}^{3}f(\tau_{i})g(t-\tau_{i})=f(\tau_{1})g(t-\tau_{1})+f(\tau_{2})g(t-\tau_{2})+f(\tau_{3})g(t-\tau_{3})
畳み込み積分の原型が完成します。f(\tau_{i})g(t-\tau_{i})というのは、時間t=\tau_{i}の時に大きさf(\tau_{i})の衝撃を何かしらの機構に加えた時の応答を表しています。この機構はシステムと呼ばれます。こんなイメージです。

時間t=\tau_{1},\tau_{2},\tau_{3}に衝撃f(\tau_{1}),f(\tau_{2}),f(\tau_{3})を与えた時のシステムの応答は先ほど足し合わせた結果になります。このあたりの説明は調べればもっと分かりやすいのもありますし、筆者も以下の記事で畳み込み積分に触れています。
https://zenn.dev/torataro/articles/2023-08-12-linear_system
もし衝撃を連続的に与えれば総和記号ではなく、積分で表す必要が出てくるでしょう。これはもはや衝撃ではなく単なる入力です。f(t)という関数を絶えずシステムに入力していることになります。その時の応答が畳み込み積分なのです。
相関関数とは?
相関とは二つのデータがどれだけ似ているかを示す指標です。音声のような二つの一次元データ\bm{a}=(a_{i}),\bm{b}=(b_{i})を例にあげてみます。データ\bm{a},\bm{b}の平均は0とします。
r(\bm{a},\bm{b}) = \frac{\sum_{n=1}^{N}a_{n}b_{n}}{\sqrt{\sum_{n=1}^{N}(a_{n})^{2}}\sqrt{\sum_{n=1}^{N}(b_{n})^{2}}}
このrは相関係数といい-1から1までの値をとるものです。データ\bm{a}と\bm{b}が似ている場合、相関係数は1に近い値をとります。\bm{a}=\bm{b}であれば相関係数は1となります。ここで、
\langle\bm{a},\bm{b}\rangle=\sum_{n=1}^{N}a_{n}b_{n}
は\bm{a}と\bm{b}の内積と呼ばれ、相関係数の分子に当たります。データの類似性を考えるならば分子の内積だけで議論でき、似ていれば似ているほど内積は大きな値をとります。この考え方を関数に拡張します。関数f,gの内積は、
\langle f,g\rangle=\int_{-\infty}^{\infty}f(\tau)g(\tau)d\tau
で定義されます。さらにtも使ってf,gの相対的なずれを表現すると、
R_{fg}(t)=\int_{-\infty}^{\infty}f(\tau)g(\tau-t)d\tau
と相関関数が出来上がります。特にf=gの時は自己相関関数、f\ne gの時は相互相関関数と呼ばれます。自己相関関数のイメージを描いておきます。
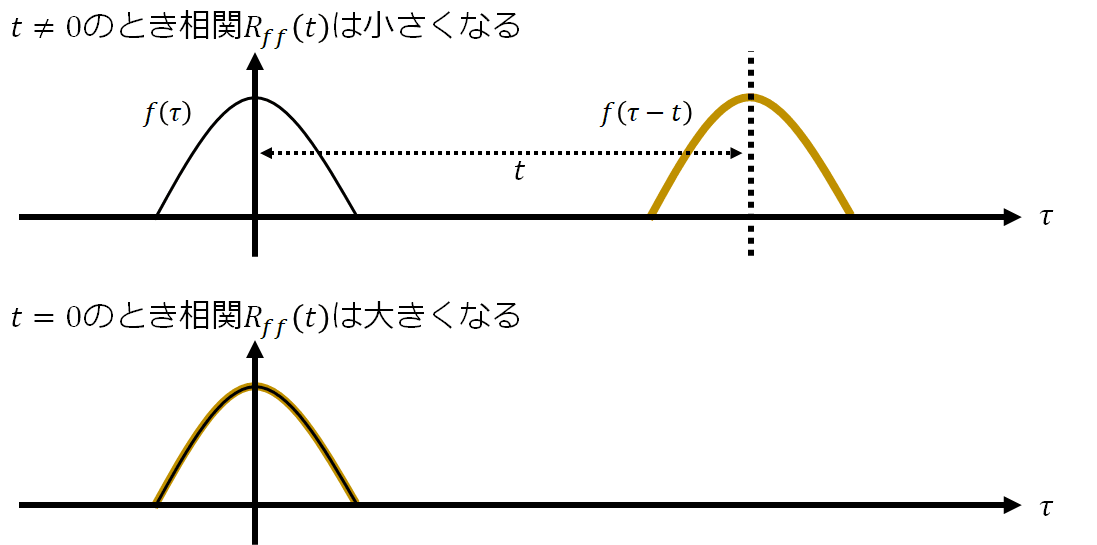
これまでの話を踏まえるならば、関数の類似性を表すとき内積で十分なように見えますが、tでずれを表現するメリットは何でしょうか?それは関数の性質を記述できる点にあります。例にホワイトノイズw(\tau)をあげましょう。ホワイトノイズはこんな波形です。
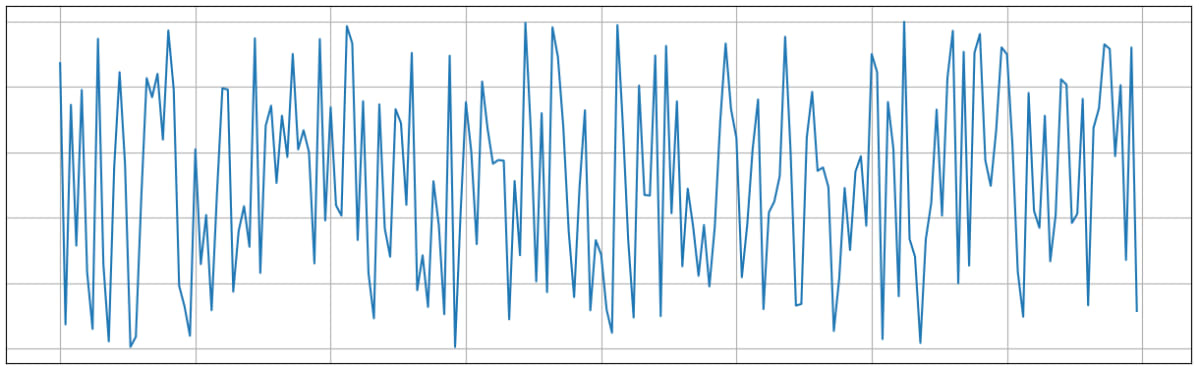
一見、なんの規則性もなさそうな波形ですが、自己相関関数を使って解析すると、
R_{ww}(t)=
\left\{
\begin{array}{ll}
\infty & t=0 \\
0 & t\ne 0
\end{array}
\right.
となります。つまりt=0でないと一切相関を持たないということです。これはホワイトノイズの特徴です。
それぞれの違いとは?
これまでの話をまとめましょう。
- 畳み込み積分はとある入力に対するシステムの応答を表すもの。
- 相関関数は二つの関数の類似性を表すもの。
これが畳み込み積分と相関関数の決定的な違いになります。
畳み込みニューラルネットワークは畳み込みではない?
現在、生成AIの台頭であまり名前を聞かなくなった畳み込みニューラルネットワーク(CNN)ですが、CNNは畳み込みというより相関の原理で説明されるべきものです。それを紹介します。
CNNの原理
CNNは入力した画像の特徴量を抽出し、抽出した特徴量から推論などのタスクをこなすアーキテクチャです。例えばこんなアーキテクチャを指します。
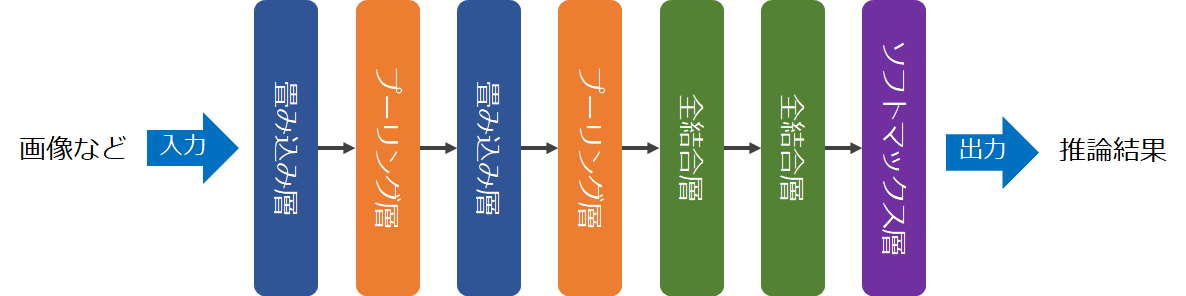
特に畳み込み層とプーリング層は特徴量抽出の核となっており、それぞれの役割は次の通りです。
- 畳み込み層:画像から特徴量を抽出する。
- プーリング層:抽出した特徴量からノイズ耐性のある特徴量を抽出する。
ノイズ耐性があるというのはロバスト性を持つとも言われます。とりわけ直接画像の特徴量を抽出する部分として畳み込み層があるわけですが、次にその原理を説明します。
畳み込み層と相関
今回畳み込み対象となるデータは画像なので、その畳み込みは二次元でかつ離散的です。例えば画像\bm{X}=(X_{i,j})とフィルタ\bm{W}=(W_{i,j})の畳み込み\bm{Y}=(Y_{i,j})は、
Y_{k,l}=\sum_{i=-\infty}^{\infty}\sum_{j=-\infty}^{\infty}X_{i,j}W_{k-i,l-j}
となります。フィルタとは画像に対して特定の処理を施すもので、平均値フィルタだと出力される画像\bm{Y}は入力画像\bm{X}と比較して滑らかなものとなります。ここでフィルタ\bm{W}=(W_{i,j})に対して新たなフィルタ\bm{W}'=(W_{-i,-j})を作成します。要は、
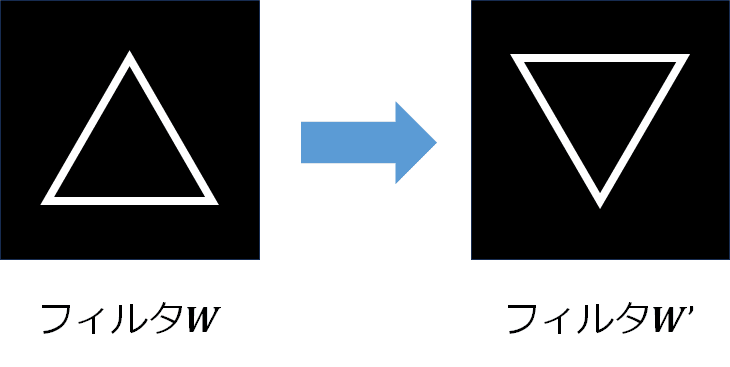
と180度くるっと回転させたものになります。そして
W_{-(k-i),-(l-j)}=W_{i-k,j-l}
より、画像\bm{X}とフィルタ\bm{W}'の畳み込み\bm{Y}'=(Y'_{i,j})は
Y'_{k,l}=\sum_{i=-\infty}^{\infty}\sum_{j=-\infty}^{\infty}X_{i,j}W_{i-k,j-l}
となります。実はこれ画像\bm{X}とフィルタ\bm{W}の相関です。画像\bm{X}からフィルタ\bm{W}に似ている要素を抽出しているのです。もしフィルタ\bm{W}を抽出したい特徴量とすれば、(k,l)ピクセル周りの画素がその特徴量を持っているかがY'_{k,l}の大きさを調べることで確認することができます。CNNにおける畳み込みはこの相関をとることを言います。
最後に
ここまで畳み込みと相関は異なるものだと説明しましたが、数式上は大きな違いがないのは明らかです。もし畳み込み積分の定義から相関の意味が見いだせれば、それを相関とみなしても問題ないです。ただ本記事では「工学的には畳み込みと相関はこのように解釈しますよ」と主張しただけにすぎません。この点に注意して良い信号処理、機械学習ライフを送ってください。最後まで読んでいただきありがとうございました!







Discussion