工学で学ぶ線形システムとは何か？

線形性とは？

線形性とは数学的には写像の性質にあたります。写像$f$に対して変数$x,y$の写像の入力とします。そして写像$f$が線形性を持つとは次のように表されます。

$$\begin{align*} f(x+y)&=f(x)+f(y) \\ f(ax)&=af(x) \end{align*}$$

つまり線形性とは足し合わせの入力は各出力の足し合わせである。また入力の定数倍$a$はその出力の定数倍$a$になると言えるでしょう。これらの性質をまとめて

$$f(ax+by)=af(x)+bf(y)$$

と書かれることもあります。逆に線形性が成り立たないのは非線形と言います。簡単な例としては、

$$f(x)=x^{2}$$

が挙げられるでしょう。これは明らかに線形性を満たしていません。しかし工学の世界では様々なシステムが線形性を満たしています。次にそれを深掘りしていきましょう。

システムとは？

システムとはとある入力に対してたった一つの出力を与えるものです。要するに数学でいう写像のことです。ただその入力は$1,2$のような数字よりは$f,g$などの関数になります。システムは$\mathcal{S}$と置いたとき、入力$f$に対して次のように書かれます^[1]。

$$f'=\mathcal{S}[f]$$

ここで$f'$は出力で入力同様に関数です。図示するまでもないですが、こんなイメージです。

システムの例いくつかあげて見ます。

分野	例	入力 / 出力
回路理論	RLC回路	電圧 / 電流
機械工学	マスばねダンパ系	マスを押す力 / マスの変位
音響工学	コンサートホール	口から発せられる歌声 / ホール内に響く歌声
信号処理	周波数フィルタ	広帯域の信号 / とある周波数帯の信号
波動光学	空間	空間内を伝搬する前の光 / 空間内を伝搬した後の光

そしてシステムが線形性を持つならば次のように記述できます。

$$\begin{align*} \mathcal{S}[f+g]&=\mathcal{S}[f]+\mathcal{S}[g] \\ \mathcal{S}[af]&=a\mathcal{S}[f] \end{align*}$$

なんのひねりもないですね。最初に紹介した線形性そのまんまです。線形性を持つシステムのことを線形システムと言います。$a$はただの定数です。

システムの入力と出力は関数であるということをもう少し説明したいと思います。音響工学を例にします。口から直接発生られる歌声の音圧は時間$t$に依存するので$p(t)$と書けるでしょう。当然コンサートホール内の歌声もその音圧は時間に依存するので$p'(t)$と書けるでしょう。なのでこれらの関係は

$$p'(t)=\mathcal{S}[p(t)]$$

と書けます。この式はとある時間$t$に置ける$p(t)$という値が$p'(t)$という値に写像されたと考えられます。この表記法でも何ら問題はありません。しかし各時間で$p(t)$から$p'(t)$への写像を書き下していくのはだるいです。いっそのこと時間を切り捨てて、

$$p'=\mathcal{S}[p]$$

と書いても得られる情報は同じです。これは関数$p$から$p'$への写像であり、システムが関数の写像であることを主張しています。ただ明示的に時間を示したほうがいい場合もあります。それはシステム自身が時間に依存するかしないか議論するときです。例えばシステムが時間に依存しないというのは、

$$p'(t-\tau)=\mathcal{S}[p(t-\tau)]$$

で記述できます。つまり同じ歌声を発すればその響き方はいつでも同じになるということです。このようにシステムの性質が時間に依存しないとき、そのシステムは時不変システムといいます。さらにそれが線形性を持つならば線形時不変システムといいます。本記事では特に断らなければ、線形システムは時不変であるとします。

システムの性質を知るにはどうすればいい？

実際問題としてシステムがどんな性質を持つか分からないことが沢山あります。しかしそれはシステムのインパルス応答を調べることで明確になる場合があります。その前に少し準備します。

デルタ関数

デルタ関数について簡単に説明します。デルタ関数$\delta(t)$は次の定義です。

$$\begin{align*} \int_{-\infty}^{\infty} f(t)\delta(t-t')dt&=\int_{-\infty}^{\infty} f(t)\delta(t'-t)dt=f(t') \\ &\int_{-\infty}^{\infty} \delta(t)dt=1 \end{align*}$$

前者は$t=t'$での関数の値$f(t')$を抽出する抽出特性です。後者はデルタ関数が$1$で正規化していることを表しています。これはあくまでも定義ですが、工学の世界ではあからさまな表記のほうが受け入れられます。それは次の通りです。

$$\delta(t)= \left\{ \begin{array}{ll} \infty & t=0 \\ 0 & t\ne 0 \end{array} \right.$$

これを図化すると次のようになります。

デルタ関数は瞬間的に大きな値を示すのに適しています。たとえばピストルの破裂音です。さらにデルタ関数の表記法として次のものがあります。

$$\delta(t)=\int_{-\infty}^{\infty}\exp(i2\pi\nu t)d\nu$$

この式は周波数$\nu=-\infty$から$\nu=\infty$までのすべての正弦波$\exp(i2\pi\nu t)$の重ね合わせで、デルタ関数が表現できることを示しています。この式は

https://zenn.dev/torataro/articles/2023-02-26-fourier_transform

で導出しています。

インパルス応答とその重ね合わせ

先ほどのデルタ関数の定義を抜き出します。

$$f(t)=\int_{-\infty}^{\infty} f(\tau)\delta(t-\tau)d\tau$$

そして線形システムの性質を使って、$f(t)$をシステムに入力したときの応答（出力）を計算してみます。

$$\begin{align*} \mathcal{S}[f]&=\mathcal{S}\left[\int_{-\infty}^{\infty} f(\tau)\delta(t-\tau)d\tau\right]\\ &=\int_{-\infty}^{\infty} f(\tau)\mathcal{S}[\delta(t-\tau)]d\tau \\ &=\int_{-\infty}^{\infty} f(\tau)h(t-\tau)d\tau \end{align*}$$

ここで

$$\mathcal{S}[\delta(t)]=h(t)$$

と定義しました。この$h$はインパルス応答と呼ばれ、デルタ関数に対するシステムの応答を表します。こんなイメージです。

ここで$\mathcal{S}[f]=\int_{-\infty}^{\infty} f(\tau)h(t-\tau)d\tau$を次のように離散化しましょう。

$$\mathcal{S}[f]\approx\sum_{n=-\infty}^{\infty}f(n\Delta t)h(t-n\Delta t)$$

これを図示するならば次のようになります。

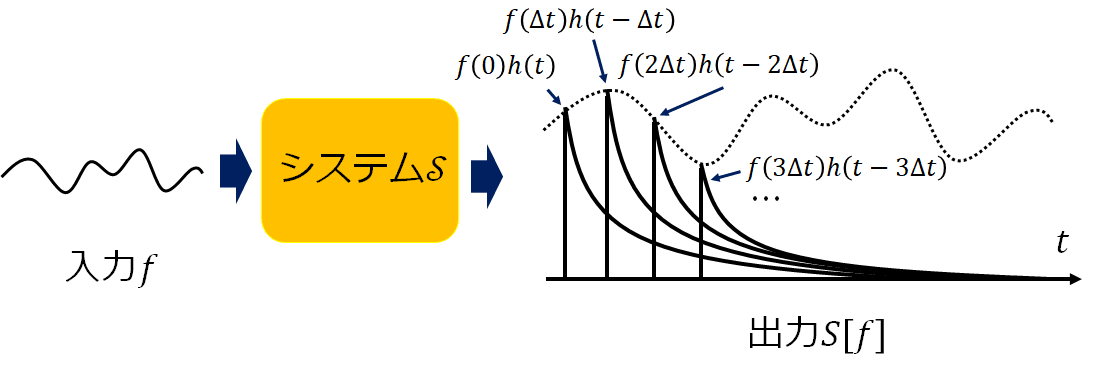
つまり関数$f$に対するシステムの応答は$h$を一つの単位としてその大きさを$f(n\Delta t)$を掛けることで大きさを調整し、後はシフト$n\Delta t$したものをすべて重ね合わせたものだということができます。ゆえにインパルス応答さえ分かれば、どんな入力があろうとも出力を予測することができるし、その意味でインパルス応答はシステムの根本的な性質を反映していると言えます。

システムの周波数特性と固有値問題

前節で現れた。$S[f]$の結果は畳み込み積分になっています。畳み込み積分$f*h$は次の定義です。

$$(f*h)(t)=\int_{-\infty}^{\infty} f(\tau)h(t-\tau)d\tau$$

そして畳み込み積分をフーリエ変換$\mathcal{F}$すると

$$\mathcal{F}[f*h]=F(\nu)H(\nu)$$

となります。フーリエ変換についてはAppendixを見てください。ここで$\mathcal{F}[f]=F(\nu),\mathcal{F}[h]=H(\nu)$としました。つまり$f$と$h$をフーリエ変換した結果の積になります。これは畳み込み積分の特徴です。

ここで注目すべきは$H(\nu)$です。これはインパルス応答$h$のフーリエ変換でシステムの周波数特性を表しています。特に$|H(\nu)|$を参照すればシステムの入力$f$が持つ周波数$\nu$の要素をどれだけ小さく（大きく）するか調べることができます。これは画像音声処理における周波数フィルタの原理です^[2]。

もう少し考察を続けましょう。$h(t-\tau)$を構成する逆フーリエ変換は次の通りです。

$$h(t-\tau)=\int_{-\infty}^{\infty}H(\nu')\exp[i2\pi\nu' (t-\tau)]d\nu'$$

システムに正弦波$\exp(i2\pi\nu t)$を入力したとき、どんな出力が得られるでしょう？実際に計算してみます。上の$h(t-\tau)$の逆フーリエ変換表現を使います。

$$\begin{align*} \mathcal{S}[\exp(i2\pi\nu t)] &= \int_{-\infty}^{\infty} \exp(i2\pi\nu \tau)h(t-\tau)d\tau \\ &= \int_{-\infty}^{\infty} \exp(i2\pi\nu \tau)\left(\int_{-\infty}^{\infty}H(\nu')\exp[i2\pi\nu' (t-\tau)]d\nu'\right)d\tau \\ &= \int_{-\infty}^{\infty}H(\nu')\exp(i2\pi\nu't) \left(\int_{-\infty}^{\infty}\exp[i2\pi(\nu-\nu')\tau]d\tau\right)d\nu' \end{align*}$$

ここで前に紹介したデルタ関数の$\exp$表現を使えば、

$$\begin{align*} \mathcal{S}[\exp(i2\pi\nu t)]&= \int_{-\infty}^{\infty}H(\nu')\exp(i2\pi\nu't)\delta(\nu-\nu')d\nu' \\ &= H(\nu)\exp(i2\pi\nu t) \end{align*}$$

要するに、

$$\mathcal{S}[\exp(i2\pi\nu t)]=H(\nu)\exp(i2\pi\nu t)$$

となります。これは線形代数で学ぶ固有値と固有ベクトルの関係そのものです。ただここでは固有ベクトルではなく固有関数になります。いわゆる関数に拡張された固有値問題なわけです。ここでは$\exp(i2\pi\nu t)$が固有関数、$H(\nu)$が固有値と呼ばれます。正弦波を入力したとき、線形システムの固有値はそのシステムの周波数特性なのです。

線形システムとは一つのモデルである。

これまで線形システムの話をしてきましたが、対象となるシステムが本当に線形であるかどうかはわかりません。というより厳密に線形性を満たしてはいないと思います。時不変でもないはずです。線形だと思ったとしてもどこか非線形な作用が含まれていると考えるのが自然です。時不変に関しても自動車のサスペンションを思い浮かべれば、バネやショックアブソーバーは劣化していきます。要は同じ入力を時が経った後に入れたとしても、同様の出力が返ってくるとは限らないわけです。

それでも線形という考え方があるのは、当然ながら非線形より扱いやすいですし、実際には非線形な要素も性能の劣化も無視できるからです。起こりえる現象をすべて把握するのではなく、より簡単なモデルに置き換えて、原理を容易に把握できるようにすることが工学の基本の考え方になります。必要であれば厳密なモデルに置き換えてやればいいのです。

Appendix

フーリエ変換と逆変換の定義

フーリエ変換$\mathcal{F}$と逆フーリエ変換$\mathcal{F}^{-1}$の定義は次の通りです。

$$\begin{align*} \mathcal{F}[f]&=\int_{-\infty}^{\infty}f(t)\exp(-i2\pi\nu t)dt \\ \mathcal{F}^{-1}[F]&=\int_{-\infty}^{\infty}F(\nu)\exp(i2\pi\nu t)d\nu \end{align*}$$

脚注

1. 入力部分ですが$\mathcal{S}[f]$で書いています。だけどこれは慣習のようなもので$\mathcal{S}\{f\}$と書く場合もあるし、$\mathcal{S}(f)$でもよいです。微分演算子と同じようにかっこは省いて$\mathcal{S}f$でもいいです。書き方は人それぞれです。

2. ハイパスフィルタ、ローパスフィルタ、などがこの原理で説明できます。