はじめに
量子コンピュータには量子アニーリング方式と量子ゲート方式の二種類があります。量子アニーリング方式は最適化問題に特化した方式ですが、汎用的に計算できる量子ゲート方式でも適切に量子ゲートを配置することで最適化問題は解けるようです。本記事ではその手法であるQAOAの原理とblueqatによる最適化問題の解法を紹介します。
最適化問題、そして量子コンピュータへ
最適化問題
最適化問題って聞いたことがあるでしょうか?もしかしたら一度は耳にしたことがあるかもしれません。簡単に説明してしまうと「とある関数の最大、最小となるような値または組合せを求める問題」です。有名どころだと巡回セールスマン問題、ナップサック問題、ポートフォリオ最適化問題があります。例えば巡回セールスマン問題だと図のような感じです。
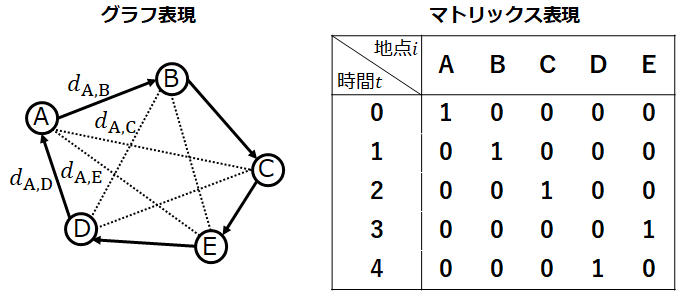
セールスマンが訪れる各地点とその間の関係を表した左の図はグラフと呼ばれます。セールスマンがとある時間tにとある地点iにいたときx_{i,t}という変数は1を取ることにします。いなければ0を取ることにします。x_{i,t}はiとtの二変数に依存する定数なので、それを右の図のようにマトリックス化することができます。そして巡回セールスマン問題の地点i,j間の距離をd_{i,j}と置くと全距離Dは次で求められそうです。
D=\sum_{i,j\in \{A,B,C,D,E\}}\sum_{t=0}^{T-1}d_{i,j}x_{i,t}x_{j,t+1}
x_{i,t},x_{j,t+1}の両方が1を取れば地点i,j間の距離が適用されます。要するにセールスマンは地点iからjに移動するのです。巡回セールスマン問題は全地点を巡回できる最小の距離Dを求めることが目標になります。
QUBO
実は最適化問題には巡回セールスマン問題のように0と1しかとらない変数を使って定式化できるものが多くあります。そこでq_{i},q_{j}\in\{0,1\}という変数を使って一般化しましょう。
H_{QUBO}=\sum_{i,j=1}^{N}C_{i,j}q_{i}q_{j}
C_{i,j}はi,j間の結合の強さを表す値です。さらにq_{i}=(q_{i})^2を考慮すれば、
H_{QUBO}=\sum_{i<j}\tilde{J}_{i,j}q_{i}q_{j}+\sum_{i=1}^{N}\tilde{h}_{i}q_{i}\;\left(\tilde{J}_{i,j}=C_{i,j}+C_{j,i},\tilde{h}_{i}=C_{i,i}\right)
で書き直せます。このHを最小化する問題をQUBO(Quadratic Unconstrained Binary Optimization)といいます。最適化問題を解く際はこのような定式化をすることが解へたどり着く第一歩となります。
イジングモデルとQUBO
物理学の話をします。物質の磁性を扱う物理モデルとしてイジングモデルがあります。イジングモデルは物質内の電子間の相互作用や、外部磁場の影響を反映した理想的な結晶です。
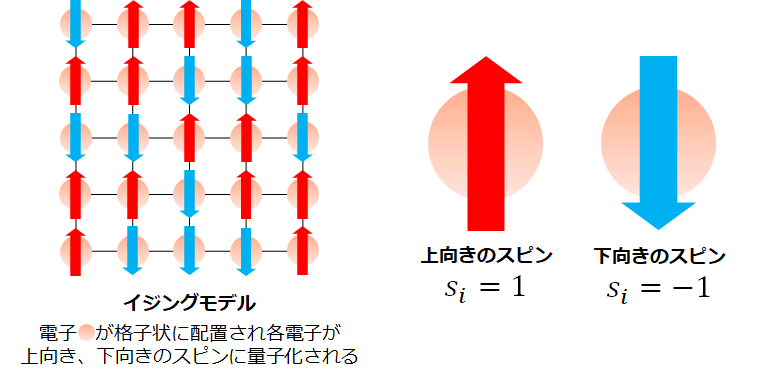
ここで主役になるのが電子のスピンです。電子には向きがあるのですが磁場を受けると上向きか下向きに量子化され、これをスピンといいます。上向きのスピンをs_{i}=1、下向きをs_{i}=-1で表したならばイジングモデルのエネルギーH_{Ising}は次のように表されます。
H_{Ising}=\sum_{i<j}J_{i,j}s_{i}s_{j}+\sum_{i=1}^{N}h_{i}s_{i}
ここでは気づくことはQUBOで定式化した式とまったく同じ形であるということです。ならばイジングモデルにおいて最小となるエネルギーを求めることこそQUBOを解くことに他ならないということになります。このような原理で動作する量子コンピュータが量子アニーリング方式と呼ばれるものです。
ただQUBOのq_{i}は0,1の変数でイジングモデルのs_{i}は-1,1の値を取る変数でした。実はこの違いはあまり気にしなくてよく、
という一対一の対応関係があるので、実際に計算するときはそれぞれの変数に置き換えてやればいいのです。
量子アニーリングの原理
イジングモデルに続いて量子力学の話をします。詳しくは僕が過去に書いた量子回路を理解しよう!part1(量子ビットまで)を見てください。簡単に説明すると量子力学は目に見えないほど小さな世界の物理学で、その状態を量子状態といい、ベクトル|\psi\rangleで表されます。これは状態ベクトルといいますが、次の式で求めることができます。
i\hbar\frac{\partial}{\partial t}|\psi(t)\rangle=\hat{H}(t)|\psi(t)\rangle
これはシュレディンガー方程式と呼ばれ、i,\hbar,tはそれぞれ虚数単位\sqrt{-1}、換算プランク定数、時間です。そして\hat{H}(t)はハミルトニアンと呼ばれエネルギーの演算子です。演算子とは関数やベクトルに作用するもので例えばd/dtや行列が該当します。さらにこれはシュレディンガー方程式でも時間に依存し、ハミルトニアンと状態ベクトルは時間を変数として持っています。
量子アニーリングでは状態ベクトルを目的の解になるようにハミルトニアンを変化させていきます。初期状態を\hat{H}_{init}、終状態を\hat{H}_{fin}とするならば、ハミルトニアンとして
\hat{H}(t)=\frac{T-t}{T}\hat{H}_{init}+\frac{t}{T}\hat{H}_{fin}
が挙げられます。t=Tで終状態になります。そして量子アニーリングとして表現される\hat{H}_{init}と\hat{H}_{fin}には
\hat{H}_{init}=\Gamma\sum_{i=1}^{N}\hat{\sigma}_{i}^{x},\;\hat{H}_{fin}=\sum_{i<j}J_{i,j}\hat{\sigma}_{i}^{z}\hat{\sigma}_{j}^{z}+\sum_{i=1}^{N}h_{i}\hat{\sigma}_{i}^{z}
があります。ここで\hat{\sigma}_{i}^{x},\hat{\sigma}_{i}^{z}\hat{\sigma}_{j}^{z},\hat{\sigma}_{i}^{z}は、
\begin{align*}
\hat{\sigma}_{i}^{x}&=\underset{(1)}{I}\otimes\cdots\otimes \underset{(i-1)}{I}\otimes\underset{(i)}{\sigma_{x}}\otimes \underset{(i+1)}{I}\otimes\cdots\otimes \underset{(N)}{I}\\
\hat{\sigma}_{i}^{z}\hat{\sigma}_{j}^{z}&=\underset{(1)}{I}\otimes\cdots\otimes \underset{(i-1)}{I}\otimes\underset{(i)}{\sigma_{z}}\otimes \underset{(i+1)}{I}\otimes\cdots\otimes \underset{(j-1)}{I}\otimes\underset{(j)}{\sigma_{z}}\otimes \underset{(j+1)}{I}\otimes\cdots\otimes \underset{(N)}{I}\\
\hat{\sigma}_{i}^{z}&=\underset{(1)}{I}\otimes\cdots\otimes \underset{(i-1)}{I}\otimes\underset{(i)}{\sigma_{z}}\otimes \underset{(i+1)}{I}\otimes\cdots\otimes \underset{(N)}{I}
\end{align*}
と略記したものです。Iは2\times 2の単位行列、\otimesはテンソル積、テンソル積の対象となる要素の下に(0),(i),(j-1)と何番目のインデックスなのかを記述しました。テンソル積に関しては量子回路を理解しよう!part2(終)を見てください。そして\sigma_{x},\sigma_{z}はパウリ行列の一つでパウリ行列はこれらを指します。
\sigma_{x}=\begin{pmatrix}
0 & 1 \\
1 & 0
\end{pmatrix},
\sigma_{y}=\begin{pmatrix}
0 & -i \\
i & 0
\end{pmatrix},
\sigma_{z}=\begin{pmatrix}
1 & 0 \\
0 & -1
\end{pmatrix}
このとき\hat{H}_{init}は横磁場(z軸に対するx軸方向)という外部磁場に関するハミルトニアンです。\hat{H}_{fin}はイジングモデルに関するハミルトニアンになります。終状態は|\psi(T)\rangleであり、H_{Ising}との関係は
\hat{H}_{fin}|\psi(T)\rangle=H_{Ising}|\psi(T)\rangle
です。量子アニーリング方式では横磁場をがっつりかけた状態から徐々に弱めることで最終的に最もエネルギーH_{Ising}が小さくなるような量子状態|\psi(T)\rangle(スピンの向き)を決定します。この向きが解になるのです。
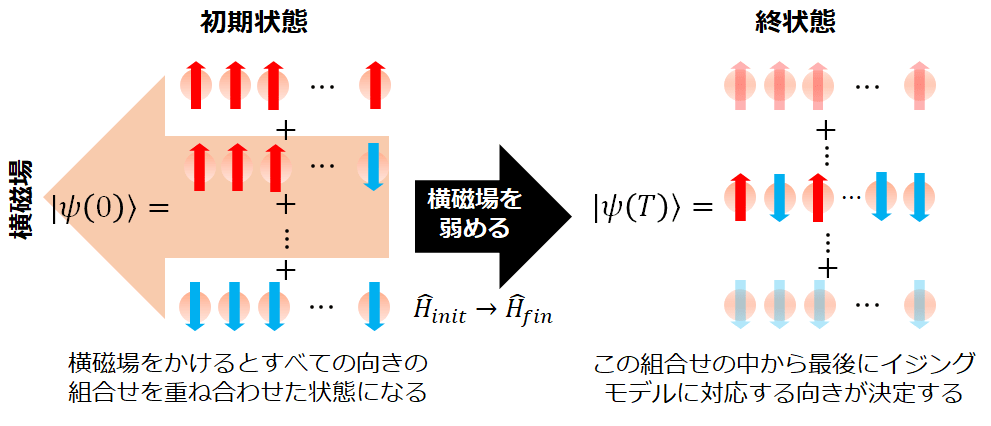
量子コンピュータではアニーリングに限らず上向きのスピンを0ビット=|0\rangle、下向きのスピンを1ビット=|1\rangleと見なします。
QAOA
QAOAの説明に入る前にシュレディンガー方程式の解を考察しましょう。初期状態|\psi(0)\rangleからほんのちょっと時間が経過した\Delta t秒後の状態|\psi(\Delta t)\rangleを導出します。簡単のためハミルトニアンは時間に依存しない\hat{H}とし、シュレディンガー方程式を離散化します。
i\hbar\frac{|\psi(\Delta t)\rangle-|\psi(0)\rangle}{\Delta t}=\hat{H}|\psi(0)\rangle\;\therefore\;|\psi(\Delta t)\rangle=\left(1-\frac{i\Delta t}{\hbar}\hat{H}\right)|\psi(0)\rangle
ここで天下り的ですが次のような演算子を導入します。
\hat{U}(t)=\exp\left(-\frac{it}{\hbar}\hat{H}\right)
\expの中に演算子が組み込まれていますが、これは
\exp(\hat{A})=1+\hat{A}+\frac{1}{2!}(\hat{A})^{2}+\frac{1}{3!}(\hat{A})^{3}+\cdots
とテイラー展開ライクに定義され\hat{U}(t)自体も演算子です。そして\hat{U}(\Delta t)は\Delta t\approx 0を考慮すれば
\hat{U}(\Delta t)\approx 1-\frac{i\Delta t}{\hbar}\hat{H}
であるので\hat{U}(\Delta t)は\Delta tだけ量子状態を変化させる演算子として働きそうです。実際t=N\Delta tと置いて\hat{U}(\Delta t)を沢山作用させれば、
\left[\hat{U}(\Delta t)\right]^{N}|\psi(0)\rangle=\hat{U}(N\Delta t)|\psi(0)\rangle=\hat{U}(t)|\psi(0)\rangle=|\psi(t)\rangle
とt秒後の状態|\psi(t)\rangleが導けます。この\hat{U}(t)は時間発展演算子と呼ばれ、状態ベクトルに作用することでt秒後の量子状態を導くものです。
時間に依存するハミルトニアンでも時間に依存しない場合の考え方が役に立ちます。というもの時間に依存したとしてほんのちょっとの時間変化はほとんど変化がない(時間に依存しない)と考えられるからです。時間依存するハミルトニアンの微小な時間変化\Delta tについても、tからt+\Delta tへの変化は
\hat{U}(t+\Delta t;t)=\exp\left(-\frac{i\Delta t}{\hbar}\hat{H}(t)\right)
という時間発展演算子で記述できると考えられます。ここで量子ゲート方式の量子コンピュータの原理を思い出しましょう。量子ゲートはとある量子状態を別の状態に変化させるものでこんなダイアグラムで記述されます。
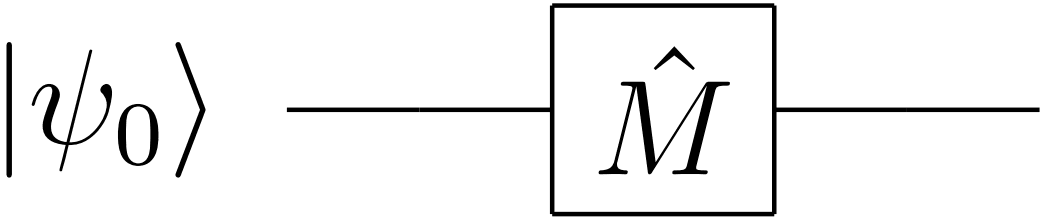
これは量子回路と呼ばれ、結局のところ\hat{M}|\psi_{0}\rangleという演算をしているにすぎません。ならば量子ゲート\hat{M}をさっき紹介した時間発展演算子\hat{U}(t+\Delta t;t)でおいて次々作用させてやれば量子ゲート方式でも最適化問題が解けるはずです。このようにして解く最適化問題はQAOA(Quantum Approximate Optimization Algorithm)と呼ばれ、量子ゲート方式での最適化問題解法の基礎原理になるものです。
blueqatの紹介
量子コンピュータの用のSDKは様々あるのですが今回はblueqat社提供のblueqatを使おうと思います。理由は簡単にコーディングできるからです。使用する場合は
でサクっとインストールできるはずです。jupyterなどだったらpipを"!pip"に置き換えてインストールしてください。早速ですが量子もつれ状態を生成する量子回路を作りましょう。量子もつれ状態を作る場合はアダマールゲート(H)とCNOTゲート(CX)が必要です。各ゲートの定義は以下のようになります。
H=\frac{1}{\sqrt{2}}\begin{pmatrix}
1 & 1 \\
1 & -1
\end{pmatrix},\;
CX=\begin{pmatrix}
1 & 0 & 0 & 0\\
0 & 1 & 0 & 0\\
0 & 0 & 0 & 1\\
0 & 0 & 1 & 0\\
\end{pmatrix}
とくにCNOTゲートについては
\begin{align*}
CX|00\rangle&=|00\rangle \\
CX|01\rangle&=|01\rangle \\
CX|10\rangle&=|11\rangle \\
CX|11\rangle&=|10\rangle \\
\end{align*}
という結果を出力します。|ab\rangleのaは制御ビットと呼ばれa=1のときbを論理回路のNOTゲートと同様フリップします。これはCNOT(Controlled NOT)と呼ばれる所以でしょう。これらの量子ゲートに作用させる2量子ビットの量子状態について初期状態を
|\psi_{0}\rangle=|00\rangle=|0\rangle\otimes|0\rangle
と置きます。ここでIを2\times 2の単位行列としたとき以下のようにゲートを作用させましょう。
\begin{align*}
|\psi_{1}\rangle=(H\otimes I)|\psi_{0}\rangle&=H|0\rangle\otimes I|0\rangle\\
&=\frac{1}{\sqrt{2}}(|0\rangle + |1\rangle)\otimes |0\rangle\\
&=\frac{1}{\sqrt{2}}(|00\rangle + |10\rangle)
\end{align*}
さらに|\psi_{1}\rangleにCNOTゲートを作用させれば
\begin{align*}
|\psi_{2}\rangle=CX|\psi_{1}\rangle&=\frac{1}{\sqrt{2}}(CX|00\rangle + CX|10\rangle)\\
&=\frac{1}{\sqrt{2}}(|00\rangle + |11\rangle)
\end{align*}
となります。これが量子もつれ状態で例えば、
\frac{1}{\sqrt{2}}(|0\rangle + |1\rangle)\otimes|0\rangle
=\frac{1}{\sqrt{2}}(|00\rangle + |10\rangle)
のように因数分解できない状態になります。量子もつれ状態について|ab\rangleのaを0で観測した場合bは必然的に0に決定し、aを1で観測した場合bは1で決定します。bの観測でもaはbに依存してaが0か1で決定します。この量子回路をblueqatで実装&実行すると以下のコードになります。
from blueqat import Circuit
q_circ = Circuit()
q_circ.h[0].cx[0, 1].m[:]
result = q_circ.run(shots=1000)
print(result)
q_circ.run(backend='draw')
めっちゃ簡潔ですね。blueqatの特徴は量子回路にゲートを与えるときメソッドチェーンというJavaScriptのような書き方ができることです。さてprint(result)の箇所はどのように表示されたでしょうか?
Counter({'11': 515, '00': 485})
これは|00\rangleという量子状態が485回、|11\rangleという量子状態が515回観測されたことを意味します。というのもこの量子回路は1000回実行しており、各実行で|00\rangleまたは|11\rangleのどちらかが観測されているのです。ちなみに量子回路もサクッと描画することができて、こんな感じで出力されます。

めっちゃ横に長いですね。左側を拡大します。
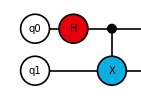
q0とq1は2量子ビットの回路のため必然的に定義された量子ビットです。特になにも操作していなければq0=0,q1=0で初期化されているはずです。そしてHと2量子ビットにまたがるXというゲートがあります。Hはアダマールゲートで2量子ビットにまたがるXがCNOTゲートです。q0のほうに●がついてますが、これはq0が制御ビットであることを示しています。次に右側を拡大します。
このMで思い当たるのはmeasure(観測、測定)なので、量子ゲートを通じて得られた量子状態を観測するところだと思ってよさそうです。さて同様の回路をIBM社提供のqiskitで書いてみましょう。インストール方法は以下の通りです。
あと量子回路記述用に
というモジュールもインストールしてください。qiskitで書いた量子もつれを生成&観測するコードが次の通りです。
from qiskit import QuantumCircuit, Aer, execute
n_bit = 2
q_circ = QuantumCircuit(n_bit, n_bit)
q_circ.h(0)
q_circ.cx(0, 1)
q_circ.measure(0, 0)
q_circ.measure(1, 1)
backend = Aer.get_backend('qasm_simulator')
exe = execute(q_circ, backend=backend, shots=1000)
result = exe.result()
print(result.get_counts())
q_circ.draw('mpl')
これを見る限りblueqatのほうが簡単に書けることが分かります。このqiskitで記述されたコードのprintで出力される観測結果は次の通りです。
また量子回路は次のように表示されます。
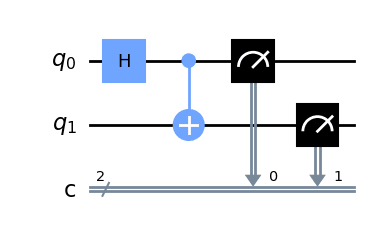
なんかよさげな回路図が出てきました。Hはアダマールゲート、2量子ビットにまたがっている+マークはCNOTゲートになります。メーターのマークは測定です。ここで気になるのが下の"c"と書かれている箇所です。これは古典ビットで我々のPCのメモリにあたり、観測した結果を格納します。このように古典ビットを明示的に表示すれば、格納された結果に応じて量子ゲートを制御するなんてことができるようになります。
QAOAで最適化問題を解いてみる
ここからblueqatを使ってQAOAを実行してみましょう。このサイトを参考にしました。
https://blueqat.com/yuichiro_minato2/4d181ab7-bcff-420c-a658-2244602b18cb
ここで最小化したい式を
H=2q_{1}-q_{2}-4q_{0}q_{1}+3q_{1}q_{2}
とします。このHはIBM Quantumで学ぶ量子コンピュータのp201から引用してきました。この式を最小化するq_{0},q_{1},q_{2}の組は(q_{0},q_{1},q_{2})=(1,1,0)です。では実際にコーディングしてみましょう。
from blueqat.utils import qaoa
from blueqat.pauli import qubo_bit as q
H = 2*q(1)-q(2)-4*q(0)*q(1)+3*q(1)*q(2)
step = 4
result = qaoa(H, step)
result.circuit.run(backend="draw")
print(result.circuit.run(backend="quimb", shots=1000))
実行した結果が次の通りです。
Counter({'110': 820, '101': 66, '111': 54, '100': 23, '010': 15, '001': 13, '000': 5, '011': 4})
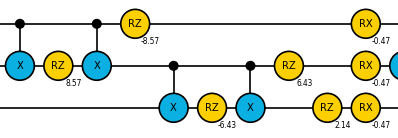
1000回の観測を行っていますが、正解である110が最も多く観測されました。このとき出力された量子回路は次の通りです。
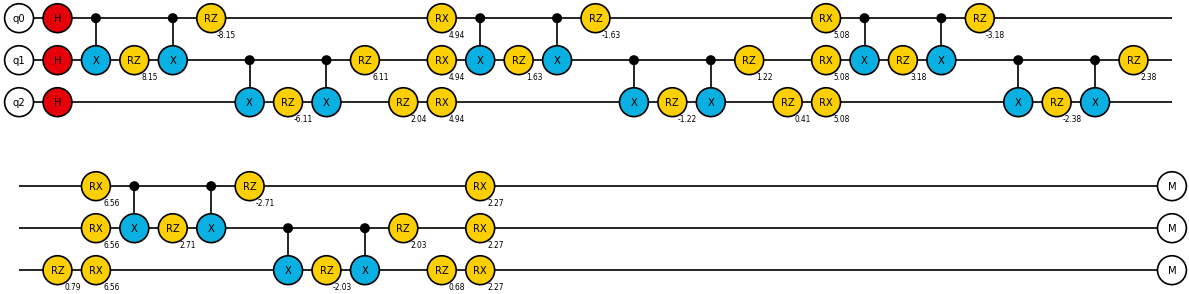
なんかすごそうな量子回路が出力されました。非常に見にくくて恐縮ですが今は深堀する必要はないです。重要なのはたったこれだけのコードで最適化問題が解けるということです。試しに上記コードのstepを2にして実行してみましょう。その時の結果と量子回路が次の通りです。
Counter({'110': 549, '101': 172, '001': 67, '000': 66, '111': 65, '010': 43, '100': 29, '011': 9})

正解である110の観測回数がいずれにしても一番多いですが549に減りました。また量子回路のボリュームも少なくなりました。今度は思い切ってstep=8で設定してみましょう。結果と量子回路は次の通りです。
Counter({'110': 872, '101': 63, '001': 46, '010': 8, '100': 7, '111': 4})

正解である110の観測回数が872回、量子回路のボリュームは思いっきり大きくなりました。ただ観測回数はstep=4の時と大きく変わらないです。試しにstepを1から10まで設定し、110を観測した回数をまとめてみます。
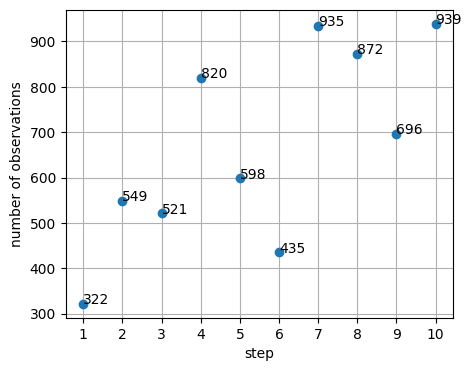
どうやらstepが大きくなるにつれ110が出現する回数は大きくなりそうです。ただ一定の法則性は見当たらないので何とも言えません。実際何回か実行してみましたが基本的にどんな値を取るかは気まぐれです。ぜひ自らの環境で実行してみることをお勧めします。
より深くQAOAを理解する
先ほどのstepなんですがどうやらこの部分の繰り返しのようです。
そして必ずQAOAでは
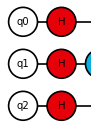
とすべての量子ビットにアダマールゲートを作用させてスタートします。この理由と繰り返しの意味について記述します。
QAOAがアダマールゲートから始まる理由
今一度時間発展演算子を参照しましょう。
\hat{U}(t+\Delta t;t)=\exp\left(-\frac{i\Delta t}{\hbar}\hat{H}(t)\right)
ここでのハミルトニアンは時間依存するハミルトニアンで
\hat{H}(t)=\frac{T-t}{T}\hat{H}_{init}+\frac{t}{T}\hat{H}_{fin}
でした。ここでt=0のとき横磁場をがっつりかけると説明しました。これは3量子ビットの最適化問題ならば、その初期状態が
|\psi_{0}\rangle=\frac{1}{\sqrt{2^{3}}}(|000\rangle+|001\rangle+|010\rangle+|011\rangle+|100\rangle+|101\rangle+|110\rangle+|111\rangle)
と000から111のすべての量子状態の重ね合わせを作っていることになります。この量子状態を作るには|q0q1q2\rangle=|000\rangleという量子回路上の初期状態から上記重ね合わせ状態を作る必要があります。それが実現するのがアダマールゲートで次のように作用させてあげれば、
\begin{align*}
(H\otimes H\otimes H)|000\rangle&=H|0\rangle\otimes H|0\rangle\otimes H|0\rangle\\
&=\frac{1}{\sqrt{2}}(|0\rangle+|1\rangle)\otimes\frac{1}{\sqrt{2}}(|0\rangle+|1\rangle)\otimes\frac{1}{\sqrt{2}}(|0\rangle+|1\rangle) \\
&=|\psi_{0}\rangle
\end{align*}
すべての重ね合わせ状態を作ることができます。アダマールゲートからスタートするのはこれが理由です。
QAOAが同じ量子回路を繰り返す意味
次に繰り返し部分です。まず
\alpha=\frac{T-t}{\hbar T},\;\beta=\frac{t}{\hbar T}
と置いてしまします。そうすると時間発展演算子は
\hat{U}(t+\Delta t;t)=\exp\left(-i\Delta t(\alpha\hat{H}_{init}+\beta\hat{H}_{fin})\right)
と書けます。これを見るとe^{a+b}=e^{a}e^{b}が通用しそうに見えますが一般的には成り立ちません。演算子に対しては次式が成り立ちます。
\exp(\hat{A})\exp(\hat{B})=\exp\left[\hat{A}+\hat{B}+\frac{1}{2}[\hat{A},\hat{B}]+\frac{1}{12}([\hat{A},[\hat{A},\hat{B}]]+[\hat{B},[\hat{B},\hat{A}]])+\cdots]\right]
これはベーカー・キャンベル・ハウスドルフの公式(BCH公式)と言います。詳しくはリー代数などの教科書を参照してください。ここで
[\hat{A},\hat{B}]=\hat{A}\hat{B}-\hat{B}\hat{A}
は括弧積などと呼ばれるものです。これは演算子の可換性(\hat{A},\hat{B}は入れ替え可能か?)を示す式で一般的に[\hat{A},\hat{B}]\ne 0です。これが慣れ親しんでいるスカラー量ならば必ず0になりますがそうではありません。しかしこのような演算子でも\epsilon\ll 1を使えば、
\exp\left[\epsilon(\hat{A}+\hat{B})\right]\approx\exp(\epsilon\hat{A})\exp(\epsilon\hat{B})
e^{a+b}=e^{a}e^{b}ライクに記述することが可能です。よって\Delta t\approx 0であることを思い出せば、時間発展演算子は
\hat{U}(t+\Delta t;t)\approx\exp\left(-i\Delta t\alpha\hat{H}_{init}\right)\exp\left(-i\Delta t\beta\hat{H}_{fin}\right)
で近似することが可能です。実は繰り返し部分は
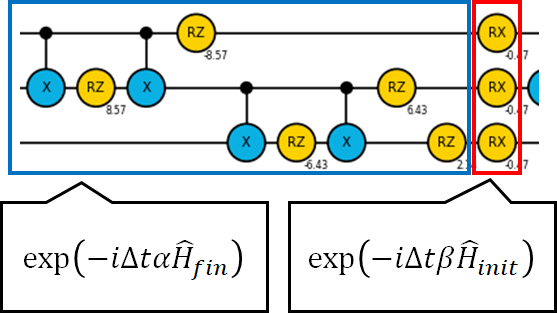
で分割されます。つまりstep1回分が\hat{U}(t+\Delta t;t)を作用させることに他ならなかったということです。
最後に
言い忘れてましたがQAOAは近似計算です。QAOAの最初のAは近似を意味する"Approximate"です。もし最適化問題を解くならば、連続的に量子状態を変化させたいところですが、量子ゲートの作用という段階的な操作で量子状態を変化させていくので、解きたい問題がQAOAで実行可能か検討するのは大切かなと思います。本記事がQAOAの入門的な立ち位置になれば幸いです。ありがとうございました!
実行環境
OS: Windows11
blueqat: 2.0.3
qiskit: 0.42.1
qiskit-aer: 0.12.0
pylatexenc: 2.10
参考文献
- 西森秀稔・ 大関真之(著)、 須藤彰三・岡真(監修)「量子アニーリングの基礎 (基本法則から読み解く物理学最前線 18) 」共立出版
- 湊雄一郎・加藤拓己・比嘉恵一朗・永井隆太郎 (著)「IBM Quantumで学ぶ量子コンピュータ」秀和システム
- 坂本眞人(著)「場の量子論 -不変性と自由場を中心にして-」株式会社裳華房



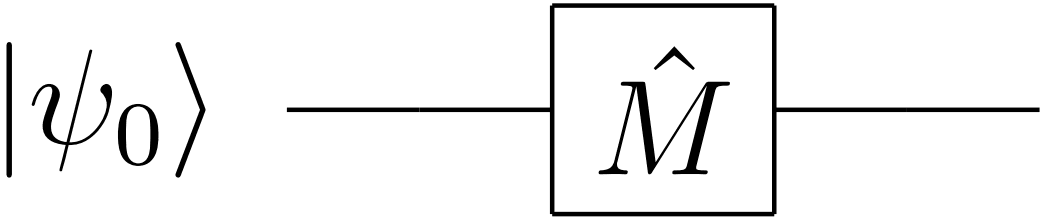















Discussion