【AHC】Rustでパーティクルフィルタ書いてみた
第一回マスターズの決勝で出題された問題で、パーティクルフィルタというものを使うっぽいのですが、よく分からないので、ネットを漁ったり、本屋で色々立ち読みしていたら、『詳解 確率ロボティクス Pythonによる基礎アルゴリズムの実装』という本が良さそうでした。
YouTubeでも解説があるので、ざっと早送りしながら見ると、雰囲気がつかめてよかったです。
本はPythonで書かれているのですが、競プロではRustを使用しているし、理解を深めるために、Rustでパーティクルフィルタによる自己位置推定を書きました。
構成
フォルダ構成に関しては以下の通りです。
main関数はa.rsに記載しており、その他はsubmit.rsを除いてモジュールです。
このボリュームになるとさすがに単一ファイルで書くのはしんどいので。。。
.
|-- Cargo.lock
|-- Cargo.toml
|-- src
| `-- bin
| |-- a.rs
| |-- agent.rs
| |-- camera.rs
| |-- common.rs
| |-- estimator.rs
| |-- motion.rs
| |-- multivariate_normal.rs # not used
| |-- normal.rs
| |-- plot.rs # not used
| |-- submit.rs # 提出用
| `-- vis.rs
`-- submit.sh # 提出用
使用するクレートに関しては、ビジュアライザを除いてAtCoderで使用できるものに限定しています。
Cargo.toml
[package]
name = "robotics"
version = "0.1.0"
edition = "2018"
# See more keys and their definitions at https://doc.rust-lang.org/cargo/reference/manifest.html
[dependencies]
proconio = { version = "=0.4.5", features = ["derive"] }
rand = { version = "=0.8.5", features = ["small_rng", "min_const_gen"] }
getrandom = "=0.2.10"
rand_chacha = "=0.3.1"
rand_core = "=0.6.4"
rand_hc = "=0.3.2"
rand_pcg = "=0.3.1"
rand_distr = "=0.4.3"
eframe = "0.19.0"
[features]
local = []
今回書いたコードは特に提出する必要はないのですが、AHCにおいては単一ファイルにまとめて提出する必要があるため、ついでなので単一ファイルにバンドルするスクリプトsubmit.shと提出ファイルsubmit.rsも書いておきました。スクリプトの記事は以下を参照。不要な人は無視してください。
また、ビジュアライザのvis.rsに関しては、以下の記事を参照してください。
多変量正規分布
本の中では多変量正規分布に関するコードはPythonのscipyを使って、サラッと書いてあります。これをRustで、かつ、AtCoderで使用できるクレートを使って書こうとしたのですが、結構詰まりました。結果としては、サンプリングはnalgebraというクレートで書けたのですが、確率密度関数はAtCoderでは使用できないnalgebra-mvnというクレートを使用しないと大変でした。AHCで使用するには計算速度的にもあやしいので、最終的にはお蔵入りとしましたが、multivariate_normal.rsというモジュールを作成したので、気になる方は参照してみてください。plot.rsはその副産物で、2次元の正規分布を描画する目的で作成しました。
結局どうしたかというと、本では多変量正規分布を作るときに、対角行列を代入していたので、各パラメータ間に相関ないとみなせば、パラメータの数だけ1次元の正規分布を用意するだけで良いということになりました。
また、一様乱数から正規分布に従う乱数を生成するために、ボックスミュラーという手法を用いて生成しています。
normal.rs
use std::{collections::VecDeque, f64::consts::PI};
use rand::Rng;
use rand_pcg::Pcg64Mcg;
#[derive(Debug)]
pub struct Normal {
mu: f64,
std: f64,
queue: VecDeque<f64>,
}
impl Normal {
pub fn new(mu: f64, std: f64) -> Self {
Self {
mu,
std,
queue: VecDeque::new(),
}
}
pub fn sample(&mut self, rng: &mut Pcg64Mcg) -> f64 {
if self.queue.is_empty() {
let (x, y) = box_muller(rng, self.mu, self.std);
self.queue.push_back(x);
self.queue.push_back(y);
}
self.queue.pop_front().unwrap()
}
pub fn pdf(&self, x: f64) -> f64 {
normal_pdf(x, self.mu, self.std)
}
}
fn box_muller(rng: &mut Pcg64Mcg, mu: f64, std: f64) -> (f64, f64) {
let u1 = rng.gen::<f64>();
let u2 = rng.gen::<f64>();
(
mu + (-2.0 * u1.ln() * std.powf(2.0)).sqrt() * (2.0 * PI * u2).cos(),
mu + (-2.0 * u1.ln() * std.powf(2.0)).sqrt() * (2.0 * PI * u2).sin(),
)
}
fn normal_pdf(x: f64, mu: f64, std: f64) -> f64 {
let v = (x - mu) / std;
// 正確には以下だが、尤度計算において定数は不要
// (-0.5 * v * v).exp() / ((2.0 * PI).sqrt() * std)
(-0.5 * v * v).exp() / std
}
問題設定
以下の条件におけるロボットの自己位置を推定せよ。
- ある一定の速度、角速度で移動するロボットがある
- ロボットの速度、角速度は既知であるが、外乱による影響を受ける
- ロボットの初期姿勢(位置や向き)が与えられる
- ロボットはカメラを有しており、位置情報が既知のランドマークを観測し、距離やロボット正面を基準とした角度を取得できる
- 取得した観測結果には外乱による影響を受ける
- 上述の外乱は実際は未知のパラメータだが、実験により得られた情報を用いることができる(AHCにおいては入力生成方法で与えられる)
入力
let input = Input {
time_span: 30.0, // sec
time_interval: 0.1, // sec
height: 10,
width: 10,
landmarks: vec![
Coord { x: -4.0, y: 2.0 },
Coord { x: 2.0, y: -3.0 },
Coord { x: 3.0, y: 3.0 },
],
// ロボット初期姿勢
init_pose: Pose {
coord: Coord { x: 0.0, y: 0.0 },
theta: 0.0,
},
radius: 0.2, // ロボット半径, m
nu: 0.2, // ロボットの前方方向の速度, m/s
omega: 10.0_f64.to_radians(), // ロボットの中心の角速度, rad/s
};
// 実験により得た各ノイズの標準偏差
let nn_std = 0.19;
let no_std = 0.001;
let on_std = 0.13;
let oo_std = 0.2;
let distance_rate_std = 0.14;
let direction_std = 0.05;
外乱シミュレーション用パラメータ
本の中では、様々な外乱が記載されており、コードにも反映していますが、今回は以下に限定しています。
Agent構造体にはたくさんの外乱シミュレーション用のメソッドを用意したので、適宜使用して遊んでください。
// 動作ノイズ(実際は未知のパラメータ)
let noise_per_meter = 5.0; // 道のりあたりに踏みつける小石の期待値
let noise_std = PI / 60.0; // 小石を踏んだ時にずれる角度の確率密度関数(正規分布)
agent.set_motion_noise(noise_per_meter, noise_std);
// 観測ノイズ(実際は未知のパラメータ)
let distance_noise_rate = 0.1; // 単位観測長当たりの観測距離ノイズの標準偏差
let direction_noise = PI / 90.0; // 観測角度ノイズの標準偏差
agent.set_camera_noise(distance_noise_rate, direction_noise);
パーティクルフィルタの流れ
パーティクルフィルタの流れは以下の通りです。
これは私の理解を噛み砕いて説明しており、厳密性に欠けると思うので、詳細は本をみてください。
- 初期位置が与えられるので、最初のパーティクルを初期位置に設定。
- インターバル分時間経過(ロボット移動)。
- 直前のパーティクルの位置情報から各パーティクルについて、移動速度に従い移動(状態方程式による遷移)。この際、正規分布に従う外乱を付与。
- ロボットのカメラにより、現在のランドマークの位置情報取得。
- 各パーティクルにおいて、実際に位置情報を得られたランドマークを観測した場合の尤度を計算(ベイズの定理)。
- 尤度で重みづけして、リサンプリング(尤度が小さいパーティクルはフィルタリングされる)。
- 最も尤度が高いパーティクルを自己位置と推定
- 2に戻り繰り返す
関連コードを以下に抜粋します。
パーティクルフィルタ関連コード抜粋
for _ in 0..max_turn {
let observation = agent.action(&input.landmarks);
estimator.decision(&observation, &input.landmarks);
}
pub fn action(&mut self, landmarks: &[Coord]) -> Vec<Observation> {
self.motion.state_transition_with_noise(
&mut self.rng,
self.time_interval,
&mut self.pose,
self.radius,
self.nu,
self.omega,
);
self.pose_records.push(self.pose);
let obs = self.camera.observe(&mut self.rng, self.pose, landmarks);
self.obs_records.push(obs.clone());
obs
}
#[derive(Debug)]
pub struct Estimator {
pub rng: Pcg64Mcg,
pub time_interval: f64,
pub radius: f64,
pub nu: f64,
pub omega: f64,
pub prev_nu: f64,
pub prev_omega: f64,
pub particles: Vec<Particle>,
pub motion_noise_pdf: MotionNoisePdf,
pub distance_rate_std: f64,
pub direction_std: f64,
pub pose_records: Vec<Vec<Pose>>,
pub best_weight_records: Vec<usize>,
}
impl Estimator {
pub fn new(
time_interval: f64,
init_pose: Pose,
radius: f64,
nu: f64,
omega: f64,
particle_num: usize,
motion_noise_pdf: MotionNoisePdf,
distance_rate_std: f64,
direction_std: f64,
) -> Self {
Self {
rng: Pcg64Mcg::seed_from_u64(0),
time_interval,
radius,
nu,
omega,
prev_nu: 0.0,
prev_omega: 0.0,
particles: vec![Particle::new(init_pose, 1.0); particle_num],
motion_noise_pdf,
distance_rate_std,
direction_std,
pose_records: vec![vec![init_pose; particle_num]],
best_weight_records: vec![0],
}
}
pub fn update_motion(&mut self, prev_nu: f64, prev_omega: f64) {
let mut poses = vec![];
for particle in self.particles.iter_mut() {
let (nn_noise, no_noise, on_noise, oo_noise) =
self.motion_noise_pdf.sample(&mut self.rng);
let noised_nu = prev_nu
+ nn_noise * (prev_nu.abs() / self.time_interval).sqrt()
+ no_noise * (prev_omega.abs() / self.time_interval);
let noised_omega = prev_omega
+ on_noise * (prev_nu.abs() / self.time_interval).sqrt()
+ oo_noise * (prev_omega.abs() / self.time_interval);
particle.pose =
state_transition(self.time_interval, particle.pose, noised_nu, noised_omega);
poses.push(particle.pose.clone());
}
self.pose_records.push(poses);
}
pub fn updater_observation(&mut self, observation: &Vec<Observation>, landmarks: &[Coord]) {
for particle in self.particles.iter_mut() {
for obs in observation.iter() {
let mark = landmarks[obs.id];
let obs_particle = observe_landmark(&particle.pose, &mark, obs.id);
let distance_std = self.distance_rate_std * obs_particle.dist;
let distance_normal = Normal::new(obs_particle.dist, distance_std);
let direction_normal = Normal::new(obs_particle.angle, self.direction_std);
particle.weight *= distance_normal.pdf(obs.dist);
particle.weight *= direction_normal.pdf(obs.angle);
}
}
}
// 系統サンプリング
pub fn resampling(&mut self) {
let mut ws = vec![];
let mut s = 0.0;
self.particles.iter().for_each(|particle| {
s += particle.weight;
ws.push(s);
});
if s < 1e-100 {
ws = ws.iter().map(|x| x + 1e-100).collect();
s += 1e-100;
}
let step = s / self.particles.len() as f64;
let mut r = self.rng.gen_range(0.0..step);
let mut pos = 0;
let mut particle = vec![];
let mut best_particle_idx = 0;
let mut best_weight = std::f64::MIN;
while particle.len() < self.particles.len() {
if r < ws[pos] {
if best_weight < self.particles[pos].weight {
best_weight = self.particles[pos].weight;
best_particle_idx = particle.len();
}
self.particles[pos].weight = 1.0;
particle.push(self.particles[pos]);
r += step;
} else {
pos += 1;
}
}
self.particles = particle;
self.best_weight_records.push(best_particle_idx);
}
pub fn decision(&mut self, observation: &Vec<Observation>, landmarks: &[Coord]) {
self.update_motion(self.prev_nu, self.prev_omega);
self.prev_nu = self.nu;
self.prev_omega = self.omega;
self.updater_observation(observation, landmarks);
self.resampling();
}
}
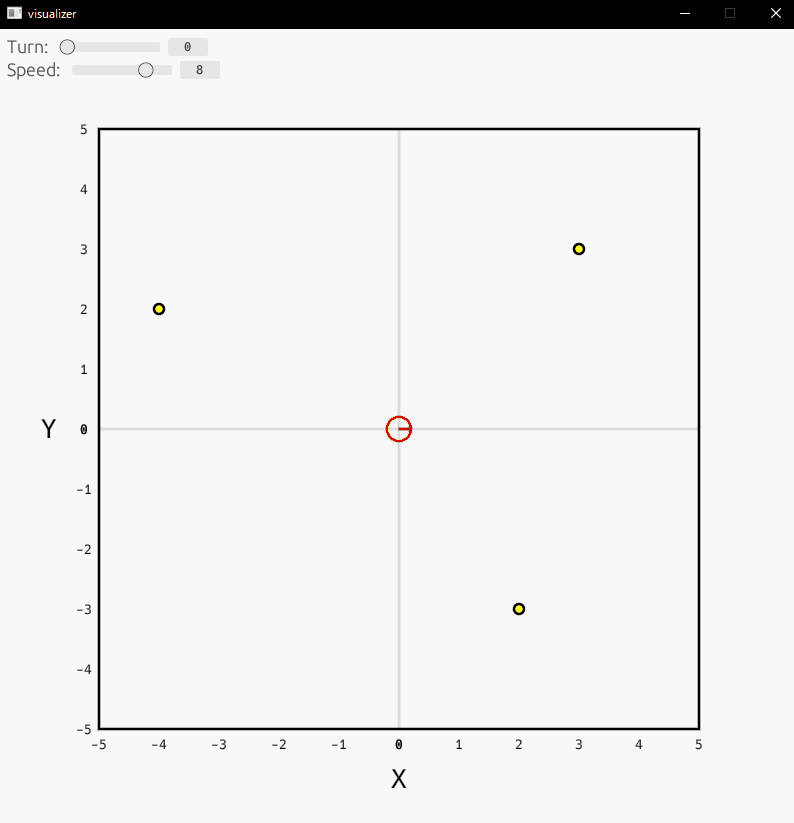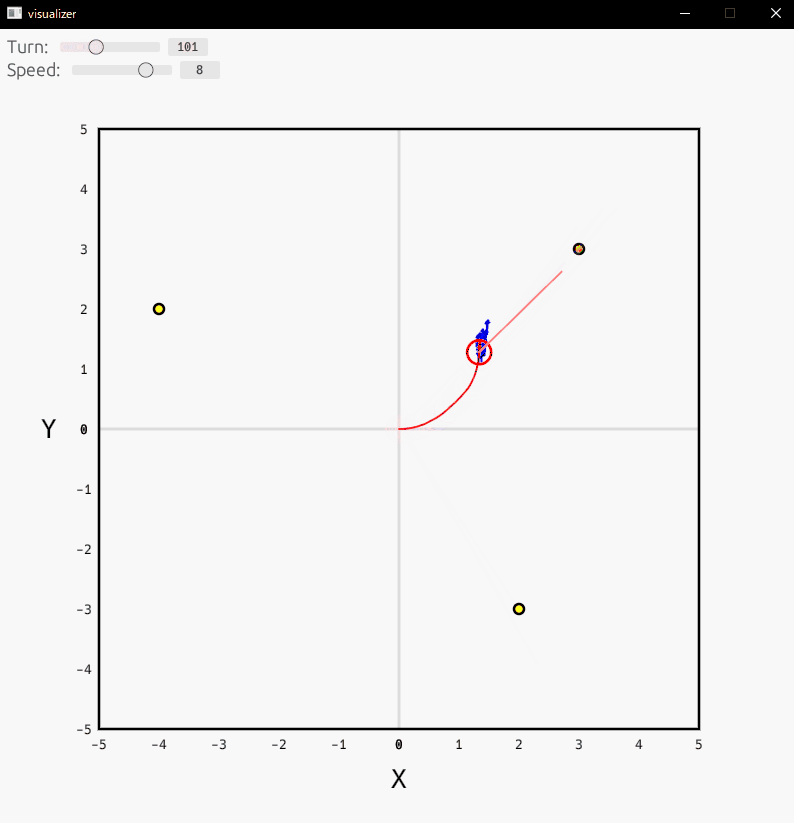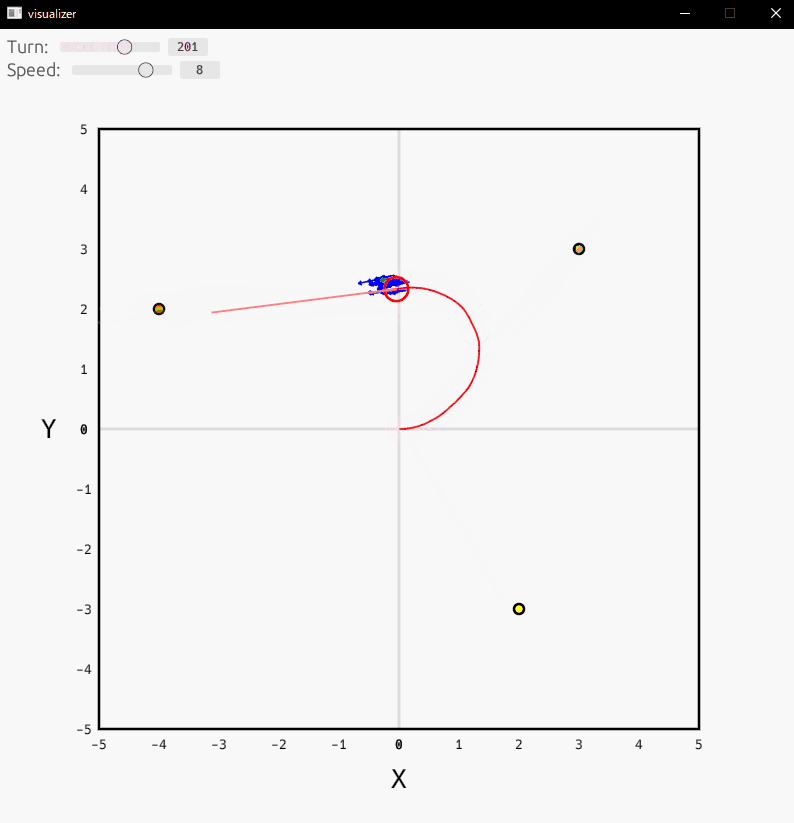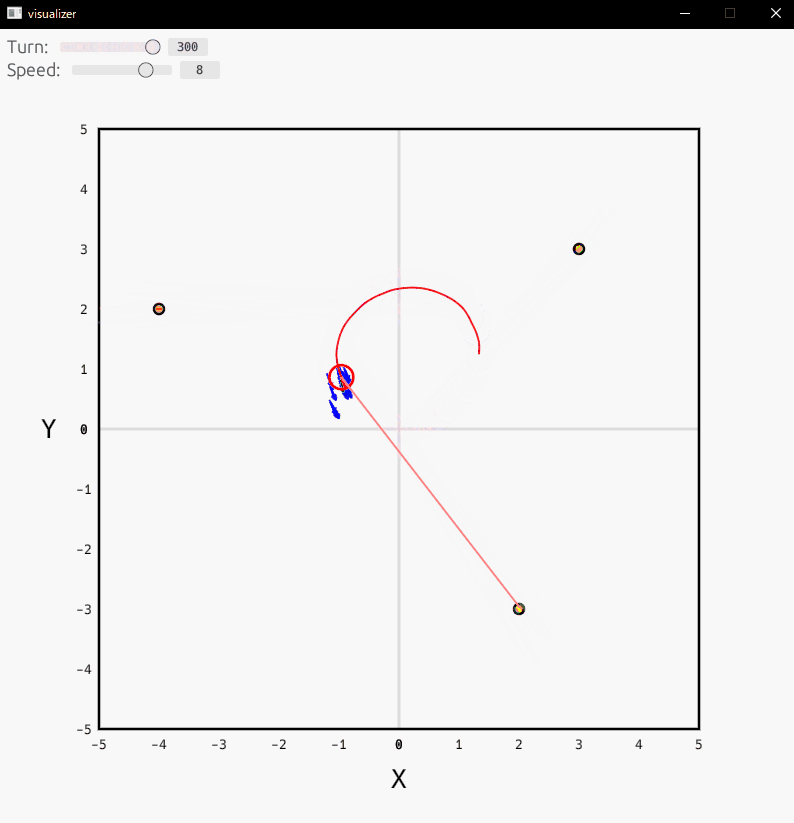
ビジュアライザ
ビジュアライザの結果は以下の通りです。
まだまだ改善の余地があるかもしれませんが、そこそこ自己位置を推定できていることを確認できます。
- 赤丸:ロボット
- 青矢印:パーティクル
- 緑矢印:最尤パーティクル
- 黄丸:ランドマーク
Discussion