Open14

制御工学

1111

制御とは

制御とは「ある目的に適合するように、対象となっているものに所要の操作を加えること」である。（JISより引用。）[1]
すなわちエアコン付きの部屋に例えて噛み砕いて言うならば、「部屋の気温」のようなあるシステム(制御対象)が存在して、「室温を快適な温度に変更する」といったある目的が存在して、その目的を達成するために「エアコンから吹き出す風の温度を調整する」といった操作を行うのが制御である。

一般に制御対象は入力と出力を持つシステムである。
例：室温の入力→エアコンから吹き出す冷たい風、出力→実際の室温

一般的にシステムへの入出力をブロック線図によって表現する。


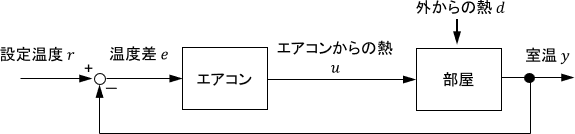
引用：ブロック線図 | こんとろラボ[2]

この制御対象に対して入力する量（操作量、制御量、制御入力）を適切に定めることによって、出力を自由に制御するのが制御工学である。[3]

制御手法の分類


制御手法の分類

人が操作量を決定するものを手動制御、制御システムによって操作量を決定するものを自動制御と呼ぶ。
自動制御にもいくつかの分類がある。

  • シーケンス制御はあらかじめ定められた順序に従って、逐次制御を行う手法。
  • フィードフォワード制御は目標値に基づいてフィードバックなしで制御を行う手法。
  • フィードバック制御とは制御対象の状態をセンサ等で読み取り, それを制御システムに入力(フィードバック)することで制御入力を決定する手法。

古典制御理論

伝達関数によってシステムの入出力を表現。[4]
周波数解析
ラプラス変換
極による安定判別。
PID制御が最も有名。

現代制御理論

物理モデルを状態方程式という微分方程式によって表現。[5]
状態方程式
遷移行列
可制御・可観測

脚注

  1. https://kikakurui.com/z8/Z8116-1994-01.html ↩︎

  2. https://controlabo.com/control-terms/ ↩︎

  3. https://ja.wikipedia.org/wiki/制御工学 ↩︎

  4. https://ja.wikipedia.org/wiki/古典制御論 ↩︎

  5. https://ja.wikipedia.org/wiki/制御理論 ↩︎

1111

ラプラス変換

\int_0^\infty e^{-st} f(t) \,dt

基本的なラプラス変換の性質

t領域(時間領域)からs領域(周波数領域)への写像を用いることで、計算機による高度な計算なしで手計算によるシステムの解析を容易にしている。

1111

極

実部が0より小さいならば安定
実部が0より大きいなら不安定
実部が0のとき安定限界(振動する)

1111

オブザーバ

\begin{align} \dot{x} &= Ax + Bu \\ \dot{\hat{x}} &= A\hat{x} + Bu + H(y - \hat{y}) \\ \end{align}

式(1), (2)の差より

\begin{aligned} \dot{x} - \dot{\hat{x}} &= A(x - \hat{x}) - H(y - \hat{y}) \\ &= A(x - \hat{x}) - HC(x - \hat{x}) \\ & (ここで e := x - \hat{x} とおいて) \\ \dot{e} &= Ae - HCe \\ &= (A - HC)e \\ \end{aligned}

\dot{e} \to 0のためには行列A-HCの固有値の実部が全て負でなければならない。

定理
対(C, A)が可観測ならばA-HCの全ての固有値の値を任意に設定できるHが存在する。

\begin{aligned} u &= K_1 x + K_2 \dot{x} \\ &=\begin{pmatrix} K_1 & K_2 \\ \end{pmatrix} \begin{pmatrix} x \\ \dot{x} \\ \end{pmatrix} \\ \end{aligned}
1111

状態方程式・出力方程式

\begin{aligned} \dot{x} &= Ax + Bu \\ y &= Cx + Du \\ \end{aligned}
1111

最適制御
最適レギュレータ

エネルギーをあまり使わない制御
エネルギーや時間を考えた制御方式

評価関数

J = \int_0^\infty \{ u^TRu + x^TQx \} \,dt

評価関数Jを最小化する制御入力uを求める最適化問題

1111

Pure pursuit
MPC
MPPI
EKF
UKF

1111

緩和対数バリア関数
https://qiita.com/PozihameBaystar/items/173e3e10d7cfaea75000

バリア関数には一般的に対数関数を使用する。

\begin{aligned} f(x) &= - \log d \\ \end{aligned}

しかし上記の定義ではd \le 0の範囲において不正値となり計算を行うことができない。そこで緩和対数バリア関数というものを使用する。

f(x) = \begin{cases} -\log d & d \ge \delta\\ \frac{1}{2}\{ (\frac{z - 2\delta}{\delta})^2 - 1 \} -\log \delta & d \le \delta \\ \end{cases}