Closed18

PID制御の基礎・応用

1111

このスクラップはZennの本に移行しました

https://zenn.dev/teruyamato0731/books/00b13741a0baf2

PID制御とは

PID制御（ピーアイディーせいぎょ、Proportional-Integral-Differential Controller、PID Controller）は、制御工学におけるフィードバック制御の一種である。出力値と目標値との偏差、その積分、および微分の3つの要素によって、入力値の制御を行う方法である。[1]

PID制御とは出力値を目標値に一致させる, フィードバック制御の一種である.
古典制御の一種であるものの, 実装が簡単でありながら安定性・応答性がよいため非常によく使われている.
古くから使用されているため, 文献が多数あり実績のある情報を得やすい.
またPID制御を改良し, 性能を良くしたものも多数提案されている.
世の中の多くのシステムはPID制御で動いている.

対象読者

  • C言語やPythonなどの使用経験があり, プログラミングに対して一定の理解がある人
  • PID制御について詳しく知りたい人
  • 制御工学に興味がある人

この記事で示すこと

  • 基礎編
    • フィードバック制御の概要
    • PID制御の式とゲイン
    • PID制御のプログラムを書き, 実システムに適用する方法
  • 応用編
    • 入力飽和に対するanti-windup
    • 速度型PID制御
    • 不完全微分を使ったPID制御
    • 2自由度制御
    • 目標値のフィルタ
    • PID制御の応答をシミュレーションする方法
  • おまけ
    • PI-D制御, I-PD制御
    • カスケード制御

参考

脚注

  1. https://ja.wikipedia.org/wiki/PID制御 ↩︎

1111

基礎編

はじめにPID制御について深く理解するため, フィードバック制御とPID制御の概要を述べる.

フィードバック制御の概要

制御とは「ある目的に適合するように、対象となっているものに所要の操作を加えること」である.
人による制御(手動制御)の代わりに, 制御システムによって行う制御を自動制御という.
PID制御は自動制御のうちのフィードバック制御に分類される.

制御手法の分類

制御手法には手動制御と自動制御の2種類が存在する.
人の手によって制御入力を調整する場合は手動制御, 制御システムによって制御入力を調整する場合は自動制御と呼ばれる.
自動制御は3つに分類できる. シーケンス制御, フィードフォワード制御(FF制御)とフィードバック制御(FB制御)である[1].
シーケンス制御はあらかじめ定められた順序に従って, 逐次制御を行う手法, フィードフォワード制御は目標値に基づいてフィードバックなしで制御を行う手法である. フィードバック制御については後に述べる.
更にフィードバック制御はレギュレータとサーボ系に大別できる.
レギュレータは状態を0に収束させるもの, サーボ系は変化する目標値に状態を追従させるものである.
PID制御はフィードバック制御の(積分型)サーボ系である.

フィードバック制御

フィードバック制御とは制御対象の状態をセンサ等で読み取り, それを制御システムに入力(フィードバック)することで制御入力を決定する制御方式である.


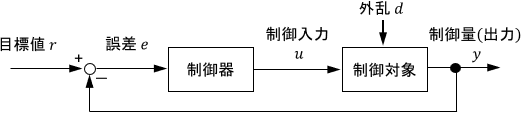
フィードバック制御のブロック線図[2]

一般的に目標値をr, 制御対象の状態を制御出力(制御量)yとし, それら目標値と実値の差を偏差eと呼ぶ. 制御対象に入力する制御入力(操作量)uの決定方法は制御システムによって異なり, フィードバック制御では偏差eによって制御入力uを決定する.

例えばモータの角速度を一定の目標値r = 3000\,\mathrm{rpm}に追従させたい場合, モータの角速度yをロータリーエンコーダ等で読み取り, 偏差e = r - yを制御器にフィードバックすることでモータに加える電圧uを決定する.

以下にフィードバック制御の方式をいくつか解説する.

オンオフ制御

定数u_cを正の値として, e(t)に応じて下記の数式により操作量u(t)を決める.

u(t) = \begin{cases} u_c & (\,e(t) > 0\,) \\ 0 & (\,e(t) = 0\,) \\ -u_c & (\,e(t) < 0\,) \\ \end{cases}

偏差e(t)が正のとき操作量をu_c, 偏差が負のとき操作量を-u_c, 偏差が0のとき操作量を0とする.

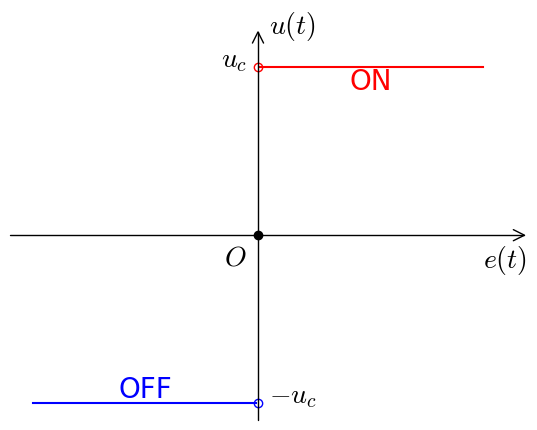
オンオフ制御による応答のシミュレーションを以下に示す. オンオフ制御では目標値に収束できていないことがわかる.

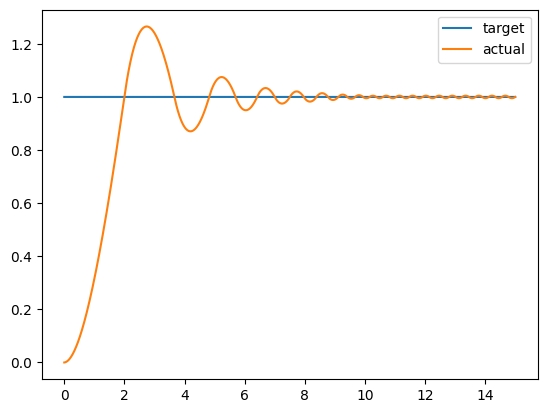
オンオフ制御による振動(ハンチング)

オンオフ制御には大きな問題点が2つある. 目標値付近で振動(ハンチング)が発生し目標値に収束しない(安定しない)点, 操作量がステップ状に大きく変動するため制御対象への負荷が大きい点である. その問題点を解決したのがP制御である.

P制御

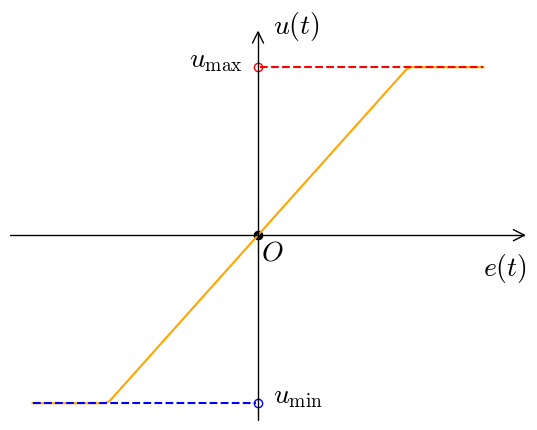
比例定数をK_pとして操作量u(t)を偏差e(t)に比例させる. これにより偏差が大きいほど出力も大きくなる. 操作量が連続に変化するため, 制御対象への負荷やハンチングが抑えられる.

u(t) = K_p e(t)


P制御に上限を加えたもの

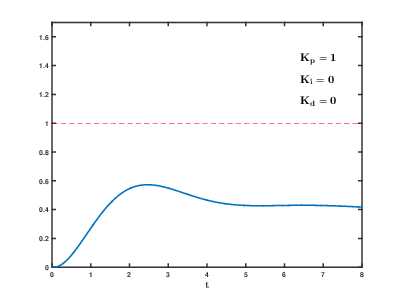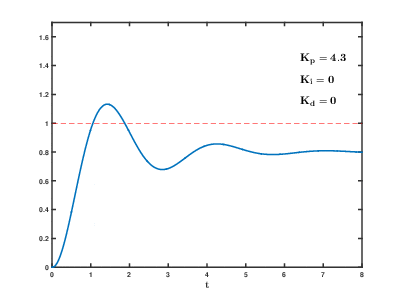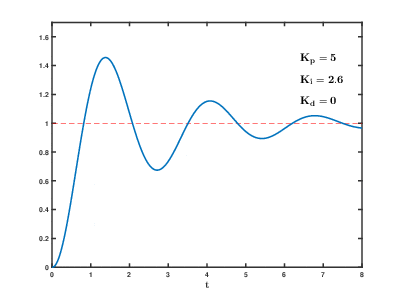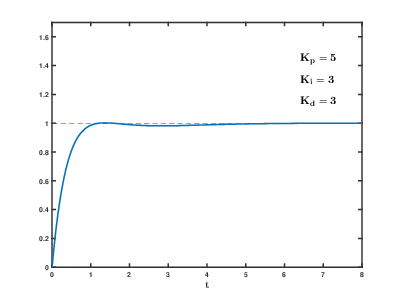
P制御による応答のシミュレーションを以下に示す. 次第に収束に向かうが, 応答のはじめは目標値を大きく通り過ぎていることがわかる.

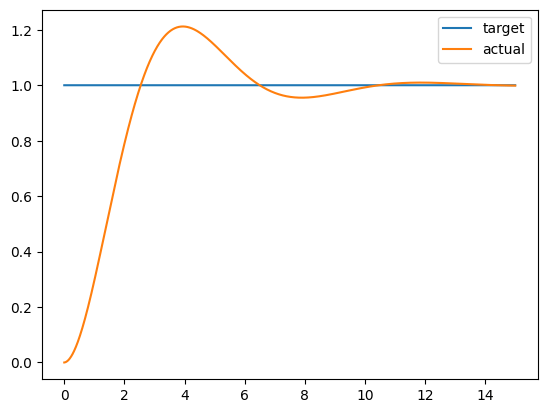
P制御によるオーバーシュート

P制御の問題点として目標値を大きく通り過ぎるオーバーシュートが挙げられる. その問題点を解決したのがPD制御である.

PD制御

P制御の問題点を解決するため, ブレーキの役割を果たすD項を追加する.
D項ではK_dを比例定数として,偏差の微分\dot{e}(t)に比例してD動作を行う.
D動作では偏差の変化量(速度)が大きいほどブレーキを強くする.
これにより速度に応じて出力を減少させることで, 目標値付近で速度をゼロにする. (未来予測)

u(t) = K_p e(t) + K_d\dot{e}(t)

PD制御による応答のシミュレーションを以下に示す.

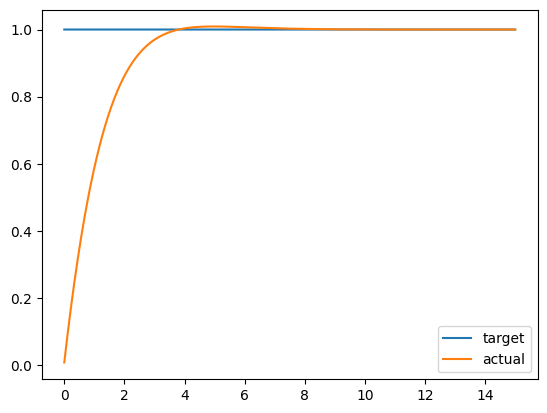
PD制御によってオーバーシュートを解決

P制御, PD制御の問題点として, いつまで経っても目標値に到達できず, 偏差が残り続けることがある. (これを定常偏差と呼ぶ. ) その問題点を解決するのがPID制御である.

PID制御

P制御, PD制御の問題点を解決するため, 定常偏差を打ち消すI項を追加する.
I項ではK_iを比例定数として, 偏差の積分(足し合わせ)に比例して出力するI動作を行う.
これにより, 偏差が残り続けた場合, I動作が大きくなることで定常偏差を打ち消す.

u(t) = K_p e(t) + K_i\int_0^t e(\tau)d\tau + K_d\dot{e}(t)

PD制御とPID制御による応答のシミュレーションを以下に示す. 下記シミュレーションでは外乱として一般的な重力を考慮し, 1方向に定常的な力を加えた.

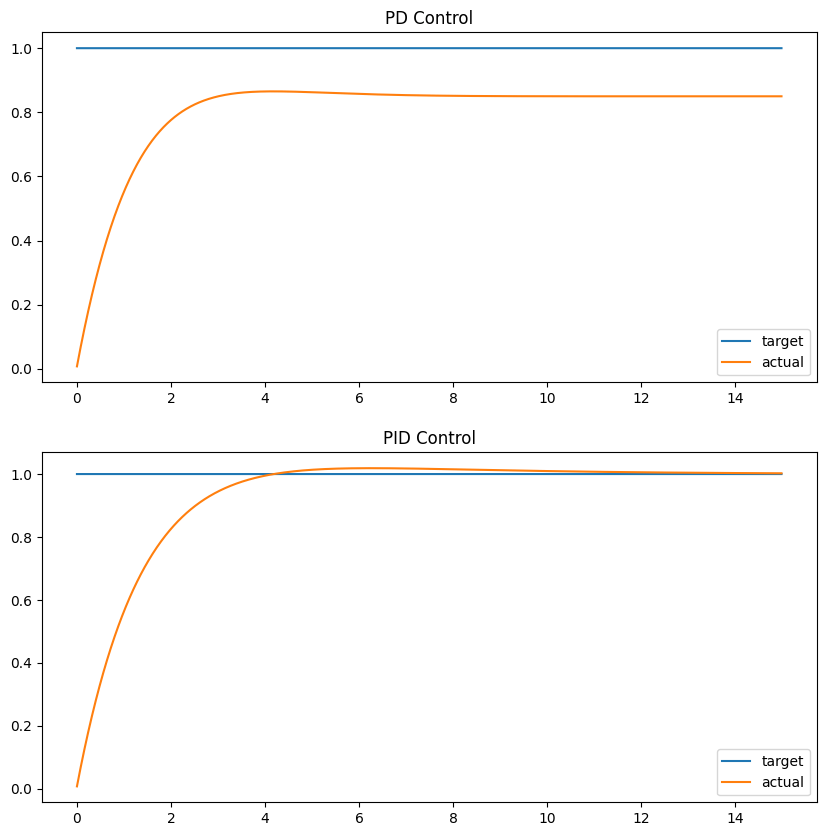
PID制御による定常偏差の打ち消し

https://controlabo.com/pid-control-introduction/

脚注

  1. https://engineer-education.com/machine-design-62_automatic-control-type/ ↩︎

  2. https://controlabo.com/control-terms/ ↩︎

1111

PID制御のブロック線図

PID制御のブロック線図は以下の通りとなる.

ブロック線図[1]

PID制御の式

あるシステムの状態を目標値 r(t) に追従させたいとき, 操作量 u(t) を以下のようにするのがPID制御である. ただしシステムの状態の実値を y(t) , 目標値と実値の偏差を e(t) とおく.

\begin{aligned} e(t) &= r(t) - y(t) \\ u(t) &= \underbrace{\vphantom{\int} K_pe(t)}_{比例P} + \underbrace{K_i\int_0^t e(\tau)d\tau}_{積分I} + \underbrace{\vphantom{\int} K_d\dot{e}(t)}_{微分D} \end{aligned}
その他の表現

PID制御の式には複数の表現方法がある.
いくつかを以下に示しておく.

媒介変数\tauを使用しない簡略版

\begin{aligned} e(t) &= r(t) - y(t) \\ u(t) &= K_p e(t) + K_i \int e(t) dt + K_d\dot{e}(t) \\ \end{aligned}

積分時間 T_i と微分時間 T_d によるもの

\begin{aligned} e(t) &= r(t) - y(t)\\ u(t) &= K_c\{e(t) + \frac{1}{T_i}\int_0^t e(\tau)d\tau + T_d\frac{de(t)}{dt}\} \end{aligned}

誤差e(t)を展開したもの

\begin{aligned} u(t) &= K_p\{r(t) - y(t)\} + K_i\int_0^t \{r(\tau) - y(\tau)\}d\tau + K_d\{\dot{r}(t) - \dot{y}(t)\} \end{aligned}

ここで K_p, K_i, K_d はP制御, I制御, D制御のそれぞれのフィードバックゲイン(比例定数)である.
P, I, Dそれぞれのゲインを変更した影響に関しては下記リンクの図がわかりやすい.

https://controlabo.com/pid-gain/

脚注

  1. https://controlabo.com/pid-control-introduction/ ↩︎

1111

数式を離散化し, プログラムを書く

上で示した式は連続時間での数式である. 実制御においては離散時間で制御を行うので離散化する.
制御周期が f[Hz] であるときの単位ステップ時間 \Delta t=\frac{1}{f}[s] を用いて, 区分求積と後退差分で近似する. ただし, r_n,y_n は既知とする. (制御周期は制御対象の特性に応じて定める. 経験知であるが私はf = 100\,\mathrm{Hz}とすることが多い. )

離散化

単位ステップ時間\Delta t[\mathrm{s}]がn回経過したとき, すなわちnステップ経過時の偏差e_nや操作量u_nを示す. リアルタイム制御において未来の情報を得ることはできないので, n+1ステップの情報を使用しないよう注意する.

\begin{aligned} e_n &= r_n - y_n\\ u_n &= K_pe_n + K_i\sum_0^n e_n\Delta t + K_d\frac{e_n - e_{n-1}}{\Delta t} \end{aligned}

プログラム用に変形

マイコン等では過去の情報をすべて記録することはできないので, 使用する情報はせいぜい2,3ステップ前までに制限する. また可読性を高めるため式は分割する.

\begin{aligned} e_n &= r_n - y_n \\ I_n &= I_{n-1} + e_n\Delta t \\ D_n &= \frac{e_n - e_{n-1}}{\Delta t} \\ u_n &= K_pe_n + K_i I_n + K_d D_n \\ \end{aligned}

プログラムを書く

この数式を下記表の通り変数で置き換えて擬似コード(Python)で示す.

意味 目標値 実際の値 偏差 前回の偏差 積分項 微分項 操作量 ステップ時間
数式 r_n y_n e_n e_{n-1} I_n,I_{n-1} D_n u_n \Delta t
変数 set_point actual error pre_error integral deriv output dt 
error = set_point - actual
integral += error * dt
deriv = (error - pre_error) / dt
output = kp * error + ki * integral + kd * deriv

C/C++でのコード例

float kp = /* ここで値を設定 */;
float ki = /* ここで値を設定 */;
float kd = /* ここで値を設定 */;

float integral = 0.0;
float pre_error = 0.0;
while(1) {
    float set_point = /* ここで値を更新 */;
    float actual = /* ここで値を更新 */;
    float error = set_point - actual;
    integral += error * dt;
    float deriv = (error - pre_error) / dt;
    // この値↓を入力として使用する
    float output = kp * error + ki * integral + kd * deriv;
    pre_error = error;
}

補足

上式は数値積分を区分求積で近似しているが, 台形則で近似したほうが精度が高い. なお実用的な精度は区分求積で十分である.

数値積分の値を台形則で近似する場合
\begin{aligned} e_n &= r_n - y_n\\ u_n &= K_pe_n + K_i\sum_0^n \frac{e_n + e_{n-1}}{2}\Delta t + K_d\frac{e_n - e_{n-1}}{\Delta t} \end{aligned} 
error = set_point - actual
integral += (error + pre_error) * dt / 2
deriv = (error - pre_error) / dt
output = kp * error + ki * integral + kd * deriv
pre_error = error
1111

PIDの応答を簡単に数式でシミュレーションしたい場合

操作量uにより制御対象の系が出力yで応答を返す場合, 大抵のシステムは一次遅れで応答するので以下によって大まかな近似計算ができる.

制御対象の時定数を\tau, 制御周期をTとして

\begin{aligned} \alpha &= \frac{\tau}{\tau + T} \\ y_{k} &= \alpha y_{k-1} + (1 - \alpha)u_{k} \\ \end{aligned}

例えば, \tau=15Tならば（時定数が制御周期の15倍）

\begin{aligned} \because \alpha &= \frac{15}{16} \\ y_{k} &= \frac{15}{16} y_{k-1} + \frac{1}{16} u_{k} \\ \end{aligned}

疑似コード

actual = 15 / 16 * actual + 1 / 16 * output

C/C++によるPID制御とシミュレーション

float kp = /* ここで値を設定 */;
float ki = /* ここで値を設定 */;
float kd = /* ここで値を設定 */;

float integral = 0.0;
float pre_error = 0.0;
float actual = 0.0;
while(1) {
    float set_point = 100.0;
    float error = set_point - actual;
    integral += error * dt;
    float deriv = (error - pre_error) / dt;
    float output = kp * error + ki * integral + kd * deriv;
    pre_error = error;

    // シミュレーション
    actual = 15.0 / 16.0 * actual + 1.0 / 16.0 * output;
    // 式を変形して以下の形でもよい
    // actual += (output - actual) / 16.0;
}
1111

応用編

PID制御にはいくつかの問題点がある. 主な2つは制御入力の飽和によるワインドアップと制御入力の急変(キック)である. 応用編ではその2つの問題点について解説した後, いくつかの解決策を示す.

制御入力の飽和

制御対象は一般に無限の制御入力を受け付けない. (例 : PWMのduty比は100%を超えることができない. モータに電流を流しすぎると発熱する. ) 過大な制御入力によって制御対象が破壊されるのを防ぐため, 上限と下限を設けるなどして操作量を制限する必要がある. 制御入力が上限もしくは下限に達した状態を, 制御入力の飽和という.
制御システムを設計する際は制御入力の飽和を考慮する必要がある.

ワインドアップとは

制御対象の特性によっては操作量の上限を迎えても目標値に到達できないことがある.
目標値に収束しないまま入力飽和が起こり続けると, 積分項が大きくなっていくワインドアップが発生する.


制御入力の制限を付けたPID制御器[1]


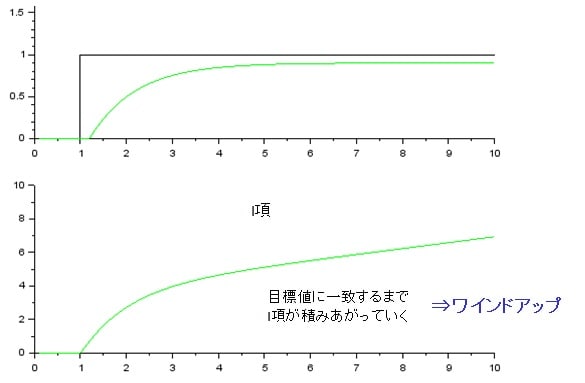
ワインドアップの発生[2]

ワインドアップが発生すると新しい目標値に対する応答遅れが発生する.[3]
ワインドアップ対策はいくつかあるが, 速度型PIDがおすすめ.

その他のワインドアップ対策
  1. 積分動作を停止する.
  2. I項に上限を設ける.
  3. 制御入力を超過している分だけI項から差し引く.

https://hamachannel.hatenablog.com/entry/2019/01/06/135004

脚注

  1. https://hamachannel.hatenablog.com/entry/2019/01/06/135004 ↩︎

  2. https://taketake2.com/N19.html ↩︎

  3. https://jp.mathworks.com/help/simulink/slref/anti-windup-control-using-a-pid-controller.html ↩︎

1111

速度型PID

通常のPID制御(位置型PID制御)の代わりに速度型PIDを使用することでワインドアップ対策となる.
通常のPID制御(位置型PID制御)と比較して, 積分が移動している.
これによってI項の積分がなくなり, 制御入力の飽和が起こってもワインドアップが発生しない. [1]

通常のPID制御(位置型PID制御)のからの変形

\begin{aligned} e(t) &= r(t) - y(t) \\ u(t) &= \underbrace{K_p e(t)}_{比例P} + \underbrace{K_i\int_0^te(\tau) d\tau}_{積分I} + \underbrace{K_d\dot{e}(t)}_{微分D} \\ \end{aligned}

2つ目の式の両辺を微分して

\begin{aligned} \dot{u}(t) &= \underbrace{K_p \dot{e}(t)}_{比例P} + \underbrace{K_i e(t)}_{積分I} + \underbrace{K_d\ddot{e}(t)}_{微分D} \\ \end{aligned}

速度型PID制御の式(連続時間)

\begin{aligned} e(t) &= r(t) - y(t) \\ \dot{u}(t) &= \underbrace{K_p\dot{e}(t)}_{比例P} + \underbrace{K_i e(t)}_{積分I} + \underbrace{K_d\ddot{e}(t)}_{微分D} \\ u(t) &= \int_0^t \dot{u}(t) dt \\ \end{aligned}

速度型PID制御の式(離散時間)

\begin{aligned} e_n &= r_n - y_n \\ \Delta u_n &= K_p \frac{e_n - e_{n-1}}{\Delta t} + K_i e_n + K_d\frac{e_n - 2 e_{n-1} + e_{n-2}}{{\Delta t}^2} \\ u_n &= \sum_0^n (\Delta u_n\Delta t) \\ \end{aligned}

プログラム用に変形

\begin{aligned} e_n &= r_n - y_n \\ P_n &= e_n - e_{n-1} \\ D_n &= P_n - P_{n-1} \\ \Delta u_n\Delta t&= K_p P_n + K_i e_n\Delta t + K_d D_n \\ u_n &= u_{n-1} + \Delta u_n\Delta t \\ \end{aligned}

疑似コード

数式 r_n y_n e_n e_{n-1} P_n P_{n-1} D_n \Delta u_n u_n, u_{n-1} \Delta t
変数 set_point actual error pre_error prop pre_prop deriv du output dt 
error = set_point - actual
prop = error - pre_error
deriv = prop - pre_prop
du = kp * prop + ki * error * dt + kd * deriv
output += du

補足 : 通常のPID制御からの変形

以下の手順を踏むことで位置型PID制御から速度型PID制御への変形を確認できる.


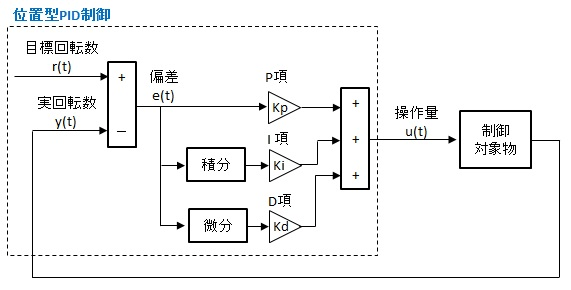
位置型PID制御


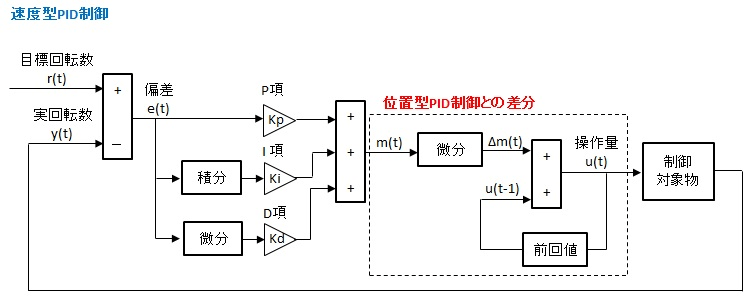
位置型PID制御の出力を微分した後, 積分


速度型PID制御(微分の位置を左に移動)

脚注

  1. https://taketake2.com/N19.html ↩︎

1111

不完全微分を使ったPID制御

D制御は微分を使用するため, 操作量の急変(キック)が発生しやすい.
これを抑えるために, D項にローパスフィルターを加えたものが不完全微分を使用したPID制御である.
不完全微分とは微分処理にローパスフィルター処理を加えた処理のことをいう. [1][2][3]

完全微分

U_D(s) = K_d s E(s)

不完全微分

\begin{aligned} U_D(s) &= K_d s E(s) \frac{1}{1+\eta Ts} \\ &= \frac{K_d s}{1+\eta Ts} E(s) \\ \end{aligned}

離散時間

ローパスフィルタの時定数は\tau = \eta \Delta tとして微分時間(単位ステップ時間？)の\eta = 0.1 \sim 0.125倍あたりで設計すればよいらしい. (詳しいことはわからない. ) 必要なカットオフ周波数に応じて設定すればよいと思う.

\begin{aligned} e_n &= r_n - y_n \\ D_n &= \frac{e_n - e_{n-1}}{\Delta t} D_{n-1} \\ D'_n &= \frac{\tau}{\Delta t + \tau} D'_{n-1} + \frac{\Delta t}{\Delta t + \tau} D_n \\ u_n &= K_p e_n + K_i \sum_0^n e_n\Delta t + K_d D'_n \\ \end{aligned}

プログラム用に変形

\tau = 7\Delta tとして\eta = \frac{1}{7} \fallingdotseq 0.14. この値を選んだ理由としてはローパスフィルタの係数が\frac{1}{8} = 2^{-3}となり, 浮動小数点の計算が早くなるため.

\begin{aligned} e_n &= r_n - y_n \\ I_n &= I_{n-1} + e_n\Delta t \\ D_n &= \frac{e_n - e_{n-1}}{\Delta t} D_{n-1} \\ D'_n &= D'_{n-1} + \frac{D_n - D'_{n-1}}{8} \\ u_n &= K_p e_n + K_i I_n + K_d D'_n \\ \end{aligned}

擬似コード

数式 r_n y_n e_n e_{n-1} I_n,I_{n-1} D_n D'_n, D'_{n-1} u_n \Delta t
変数 set_point actual error pre_error integral deriv low_pass_deriv output dt 
error = set_point - actual
integral += error * dt
deriv = (error - pre_error) / dt
low_pass_deriv += (deriv - low_pass_deriv) / 8
output = kp * error + ki * integral + kd * low_pass_deriv
脚注

  1. https://taketake2.com/N21.html ↩︎

  2. https://hi-ctrl.hatenablog.com/entry/2018/02/25/020939 ↩︎

  3. https://www.mgco.jp/rensai/pdf/r0411.pdf ↩︎

1111

組み合わせ

以上複数の対策を組み合わせた場合, 以下のようなコードとなる.

速度型PID制御 + 不完全微分

error = set_point - actual
prop = error - pre_error
deriv = prop - pre_prop
low_pass_deriv += (deriv - low_pass_deriv) / 8
du = kp * prop + ki * error * dt + kd * low_pass_deriv
output += du

速度型PID制御 + 不完全微分 + 制御入力の制限

error = set_point - actual
prop = error - pre_error
deriv = prop - pre_prop
low_pass_deriv += (deriv - low_pass_deriv) / 8
du = kp * prop + ki * error * dt + kd * low_pass_deriv
output = clamp(output + du, min, max)
1111

2自由度制御

PID制御はフィードバックのみにより出力を決定する1自由度制御である. 制御対象の特性を理解し, フィードフォワード項(FF項)を追加することで2自由度制御になる. [1]
追加するFF項の例 : 重力補償, 目標値のローパスフィルタ, ゲインスケジューリング, etc...


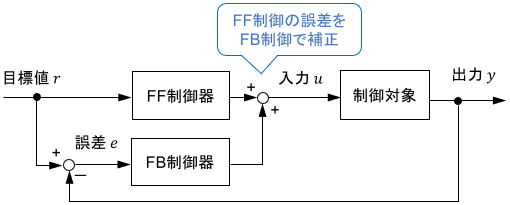
2自由度制御のブロック線図

重力補償

事前に重力の影響がわかっている場合, 重力の影響を打ち消すだけの制御出力を追加すると, 追従性や応答性の向上などが見込める.
例えば上下に移動する機構を制御するとき, 鉛直下向きに5\,\mathrm{kgf}の重力が加わっているとする. このとき上と下に移動するときで必要な力は明らかに異なる. ここで事前に5\,\mathrm{kgf}の力を打ち消すだけの制御出力をFF項として追加してあげることでPID制御側は重力を考慮せずに設計できる.

output = pid() + anti_gravity

入力整形フィルタ

目標値をステップ状に大きく変化させると制御入力のキックが発生し, 制御対象に負荷がかかるなどして望ましくない. そもそも制御対象が応答できる速度には限りがあるため, 目標値の移動速度も制御対象の応答できる速度に制限すべきである. そこで目標値を直接入力するのでなく, 参照軌道をPID制御器に入力することで, 目標値の移動速度を制限し制御入力のキックを抑える.
例えばロボットの最大移動速度が0.2\,\mathrm{m/s}だとする. このとき, 目標値を0\,\mathrm{m}から5\,\mathrm{m}まで0.2\,\mathrm{m/s}の速度で経過時間に応じて線形補完することで応答性を維持したままキックを減らせる. また目標値の移動速度を好きな値に設定することで, 制御対象の移動速度を設定することも可能となる.

後述するP-PI制御よりも入力整形フィルタのほうがおすすめ. またLPFよりも速度制限のほうがおそらく良い.
https://x.com/wataruohnishi/status/1811054271628202418

制御入力のローパスフィルタ

上記のような様々な対策を施しても制御入力にキックが発生する場合, 制御入力にローパスフィルタを挟む.

脚注

  1. https://qiita.com/getBack1969/items/d4c6ec8945f7d6a93218 ↩︎

1111

PID制御のシミュレーション

初めに制御対象の物理モデルを同定する必要がある. その後Pythonでプロットする.

下記は魔改造PID制御のシミュレーションである. 制御対象の特性に応じてFF項を追加することも多い. (重力補償など)

モデルの仮定 (2次系)

制御入力u(t)に速度v(t)が時定数\tau = 150 \,\mathrm{ms}の一次遅れで応答する物体の, 変位y(t) = \int v(t) dtを目標値r(t)に追従させる. 制御器の都合から操作量の最大値をu_{\mathrm{max}} = 0.7として|u(t)| < u_{\mathrm{max}}とする. また出力の非線形性と静止摩擦を考慮して|u(t)| < 0.1のときu(t) \simeq 0とする. このとき単位ステップ時間dt = 10\,\mathrm{ms}として離散時間におけるkステップ後のモデルの速度, 変位はそれぞれ次の式で表せる.

\begin{aligned} v_{k} &= v_{k-1} + (v_{k-1} - u_{k}) \frac{1}{16} \\ y_{k} &= y_{k-1} + v_{k} dt \\ \end{aligned}

改良版PID制御 (目標値フィルタ + anti-windup + 不完全微分)

追従速度v_{\mathrm{ref}} = 0.8 \,\mathrm{m/s}として, 目標値の移動を線形補間する. I値の飽和によるwindupを防ぐため, anti-windupとしてI値にもsaturationを実装する. キックを防ぐためD項にローパスフィルタを加え, 不完全微分とする. 制御入力にもローパスフィルタを加え, 出力の急変を抑える.

\operatorname{clamp}(x, \mathrm{lo}, \mathrm{high}) = \begin{cases} \mathrm{high} & \text{if}\ x > \mathrm{high} \\ \mathrm{lo} & \text{if}\ x >\mathrm{lo} \\ x & \text{otherwise} \\ \end{cases} \\

上記の関数を定義して

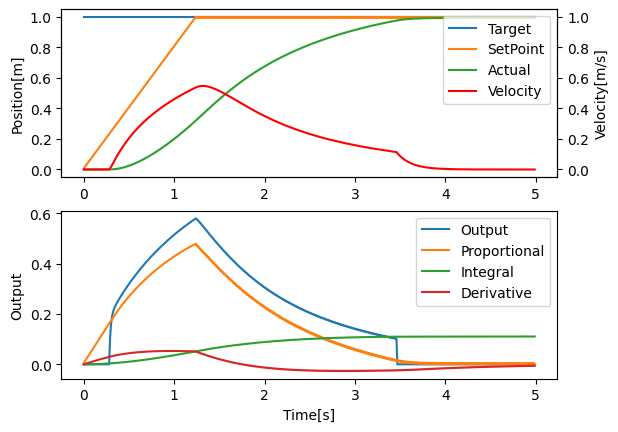
\begin{aligned} \mathrm{tag}_{k} &= \mathrm{tag}_{k-1} + \operatorname{clamp}(\mathrm{tag}_{k-1} + r_{k},\ -v_{\mathrm{ref}} dt,\ v_{\mathrm{ref}} dt) \\ e_{k} &= \mathrm{tag}_{k} - y_{k-1} \\ I_{k} &= \begin{cases} \operatorname{clamp}(e_{k} dt,\ -u_{\mathrm{max}} / K_i,\ u_{\mathrm{max}} / K_i) & (k = 0) \\ \operatorname{clamp}(I_{k-1} + e_{k} dt,\ -u_{\mathrm{max}} / K_i,\ u_{\mathrm{max}} / K_i) & (k \ne 0) \\ \end{cases} \\ D_{k} &= \begin{cases} 0 & (k = 0) \\ D_{k-1} + 0.99( \frac{ e_{k} - e_{k-1} }{dt} - D_{k-1} ) & (k \ne 0) \\ \end{cases} \\ u_{k} &= \operatorname{clamp}(K_p e_{k} + K_i I_{k} + K_d D_{k},\ -u_{\mathrm{max}},\ u_{\mathrm{max}}) \\ \end{aligned}


PID制御のシミュレーション

https://github.com/teruyamato0731/pid-simulation

1111

おまけ

おまけとして実用上必須ではないが共有したいものを示す.

PI-D制御, I-PD制御

目標値が変化したとき, P項やD項による操作量の急変(キック)が発生することがある.
このキックを防ぐために目標値との偏差 e(t) := r(t) - y(t) から目標値r(t)の影響を除き-y(t)を使用すると, PI-D制御やI-PD制御となる.
キックを防ぐことはできるものの, 目標値の影響が小さくなるので, 応答性が悪くなるデメリットが存在する.

微分先行型PID制御(PI-D制御)

D項の入力に実値と目標値との偏差 e(t) := r(t) - y(t) でなく, 実値 -y(t) を使用する.[1]

\begin{aligned} e(t) &= r(t) - y(t)\\ u(t) &= \underbrace{\vphantom{\int} K_pe(t)}_{比例P} + \underbrace{K_i\int_0^t e(\tau)d\tau}_{積分I} - \underbrace{\vphantom{\int} K_d \dot{y}(t)}_{微分D} \end{aligned} 
error = set_point - actual
integral += error * dt
deriv = (actual - pre_actual) / dt
output = kp * error + ki * integral - kd * deriv


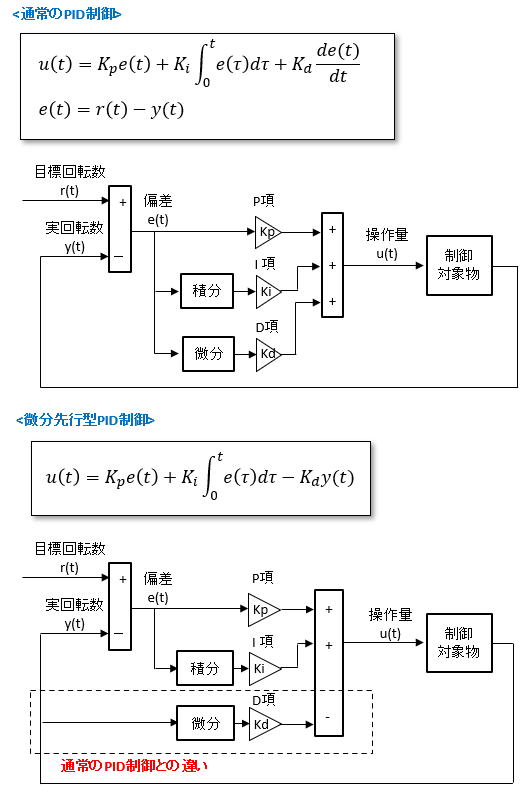
PI-D制御のブロック線図

比例微分先行型PID制御(I-PD制御)

P項, D項の両方の入力に偏差 e(t) := r(t) - y(t) でなく, 実値 -y(t) を使用する.[2]

\begin{aligned} e(t) &= r(t) - y(t)\\ u(t) &= \underbrace{K_i\int_0^t e(\tau)d\tau}_{積分I} - \underbrace{\vphantom{\int} K_p y(t)}_{比例P} - \underbrace{\vphantom{\int} K_d \dot{y}(t)}_{微分D} \end{aligned} 
error = set_point - actual
integral += error * dt
deriv = (actual - pre_actual) / dt
output = ki * integral - kp * actual - kd * deriv


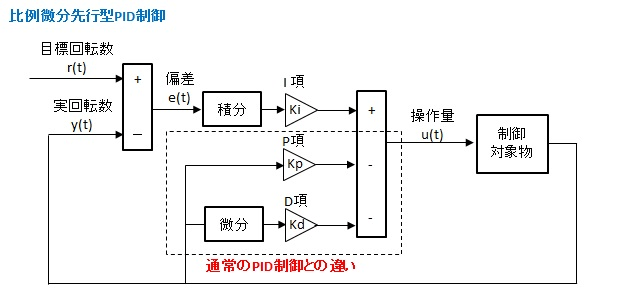
I-PD制御のブロック線図

備考

私はキックを防ぎたい場合, 目標値の変化速度を制限したり(入力整形フィルタ), 制御入力をローパスしたりするのでPI-D制御・I-PD制御はあまり使用しない.

脚注

  1. https://taketake2.com/N22.html ↩︎

  2. https://taketake2.com/N23.html ↩︎

1111

カスケード制御

カスケード制御はフィードバック制御の一種で, 二重のフィードバックループを作ることでより安定した制御を行う手法である.

例えばロボットの変位を制御したいとき, 外側のフィードバックループでロボットの目標速度を決定し, 内側のフィードバックループでモーターの角速度を制御する.

current_ref = pid(velocity_ref, velocity)
current_out = pid(current_ref, current)

https://freelance-aid.com/articles/electrical-and-electronic-design/3432.html
https://www.rkcinst.co.jp/technical_commentary/14294/
http://www.miyazaki-gijutsu.com/series/control633.html
https://tajimarobotics.com/cascade-control-basic-3/
https://controlabo.com/block-diagram-examples/

1111

C++で実装したテンプレートPID制御クラス

一般的なPID制御を行う.
T型同士とfloatとの演算が定義されていれば使用できる.
https://github.com/teruyamato0731/Chassis/blob/main/src/Pid.h#L61-L73

C++で実装した速度型PID制御クラス

D項に不完全微分を使用しており, ヘッダオンリーで使用可能.
https://gist.github.com/teruyamato0731/176ab63cc9cf74cd70c55bff12316959

使用例

https://github.com/teruyamato0731/c620_pid

Rustで実装したPID制御crate

https://github.com/teruyamato0731/advanced-pid-rs

1111

PIDによる速度の制御

PID制御は位置の制御に用いることが多い.
PID制御で速度を制御する場合, いくつかの注意が必要となる.
速度が制御入力に一次遅れで応答する1次系の場合, Pゲインを大きくするとハンチングが発生する. I動作によって制御する意識が必要である.

https://controlabo.com/pid-velocity-control/

1111

P動作は偏差をゼロにする役割, I動作は外乱による定常偏差をゼロにする役割, D動作は速度をゼロにする役割を持つ.
またI動作は位相が90°遅れ, 逆にD動作は位相が90°進む.

このスクラップは2024/03/10にクローズされました