Zenn
Closed2

ローパスフィルタまとめ

1111

ローパスフィルタとは

ローパスフィルタ(Low-Pass Filter: LPF)とは高周波成分を除去し、低周波成分を通過させるフィルタのことである。[1]
LPFで遮断する周波数をカットオフ周波数f_cという。（f_c以上の周波数信号を遮断する。）
ノイズは高周波成分であることが多いため、LPFを挟むことでノイズの除去が行える。

実用上の問題


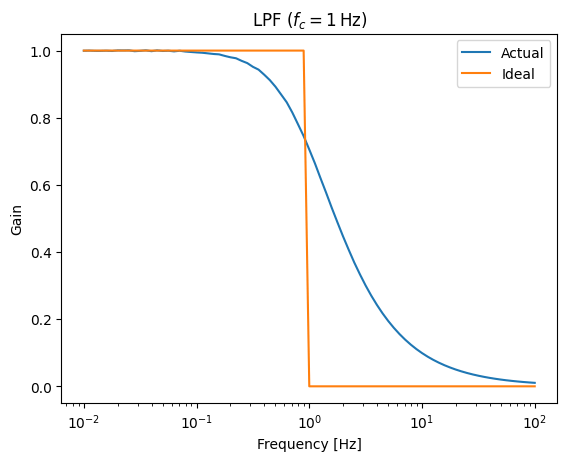
理想と現実の比較

理想のローパスフィルタではカットオフ周波数f_c以降の信号はすべてカットされる。しかし実用上のローパスフィルタは0.707倍以降をカットしたとして扱う。
また現実のローパスフィルタには位相遅れが発生する。
LPFを選定する際はカットオフ性能、位相遅れ、計算量などを比較すること。

脚注

  1. https://ja.wikipedia.org/wiki/ローパスフィルタ ↩︎

  2. https://ja.wikipedia.org/wiki/ガウス雑音 ↩︎

  3. https://watlab-blog.com/2019/04/23/gaussian-noise/ ↩︎

1111

組み込みプログラミングでよく使うデジタルフィルタ

プログラム上で実現するフィルタのことをデジタルフィルタという。[1]
今回は一般に知られている以下のフィルタを解説する。[2]

  • 一次遅れ
  • 移動平均
  • 中央値
  • 外れ値除去

一次遅れ

入力F(s)、出力Y(s)、一次遅れ要素G(s)=\frac{1}{s+a}=\mathcal{L} [e^{-a t}]とする。
出力は伝達関数と入力の積によって表せるので、これをラプラス逆変換により周波数領域から時間領域へ変換する。[3]

\begin{aligned} \mathcal{L}^{-1} [Y(s)] &= \mathcal{L}^{-1} [F(s)G(s)] \\ y(t) &= \mathcal{L}^{-1}[F(s) \frac{1}{s+a}] \\ \end{aligned}

入力f(t)=K(定数)のとき, F(s) = \frac{K}{s}なので

\begin{aligned} \mathcal{L}^{-1} [Y(s)] &= \mathcal{L}^{-1} [\frac{K}{s} \frac{1}{s+a}] \\ &= \mathcal{L}^{-1} [\frac{K}{s} - \frac{K}{s+a}] \\ y(t) &= K(1 - e^{-at}) \\ \end{aligned}

一次遅れをデジタルフィルタで用いるため、離散時間で表現する。[4][5]
kステップ後の入力f_k、出力y_k、制御周期T、時定数\tauとして

\begin{aligned} \alpha &= \frac{\tau}{T + \tau} \\ y_k &= \alpha y_{k-1} + (1 - \alpha) f_k \\ \text{カットオフ周波数} \\ f_c &= \frac{1}{2\pi\tau} \\ \end{aligned}

私がよく使う形式（T=\tau=10\,\mathrm{ms}として上式を変形）

y_k = y_{k-1} + \frac{y_{k-1} - f_k}{2} 
output += (input - output) / 2

より応答を遅くしたい場合は除数を4,8,16,\cdotsと大きくしていく。


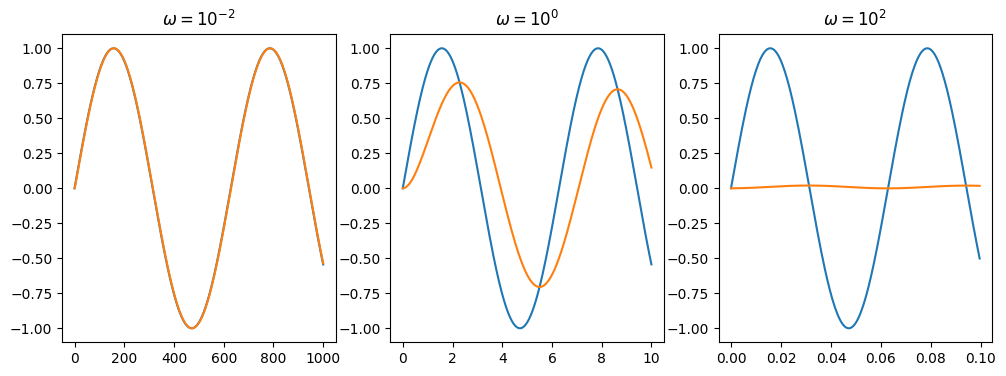
一次遅れの応答例


一次遅れのボード線図

移動平均

平均する数をNとして[6]
（カットオフ周波数の式はよくわからない）

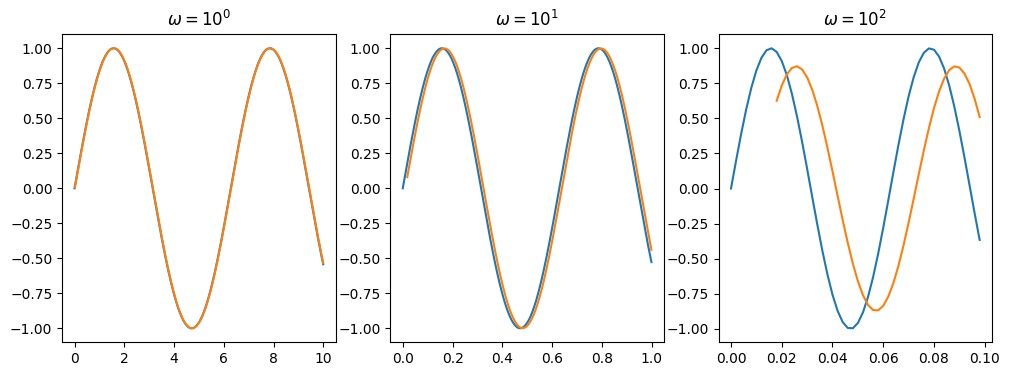
\begin{aligned} y_k &= \frac{1}{N}\sum_{i=0}^{N} f_{k-i} \\ N=3\text{のとき} \\ &= \frac{1}{3} (f_{k-2} + f_{k-1} + f_k) \\ カットオフ周波数 \\ f_c &= \frac{0.443}{\sqrt{N^2 - 1}} \frac{1}{T} \\ \end{aligned}


移動平均の応答例


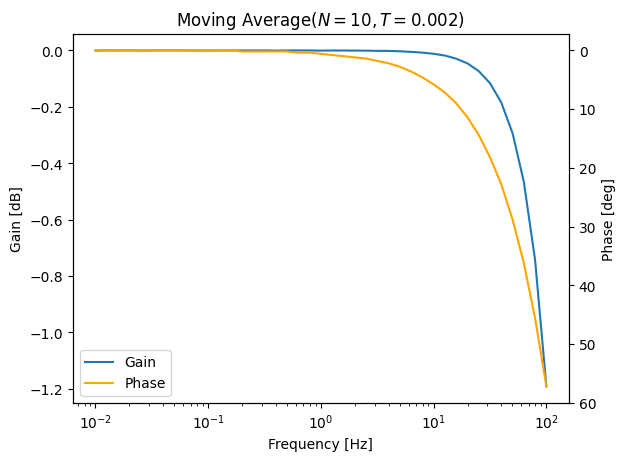
移動平均のボード線図

中央値

中央値を取る数をNとして

\begin{aligned} N=3のとき \\ y_k &= \operatorname{med}(f_{k-2}, f_{k-1}, f_k) \\ \end{aligned}


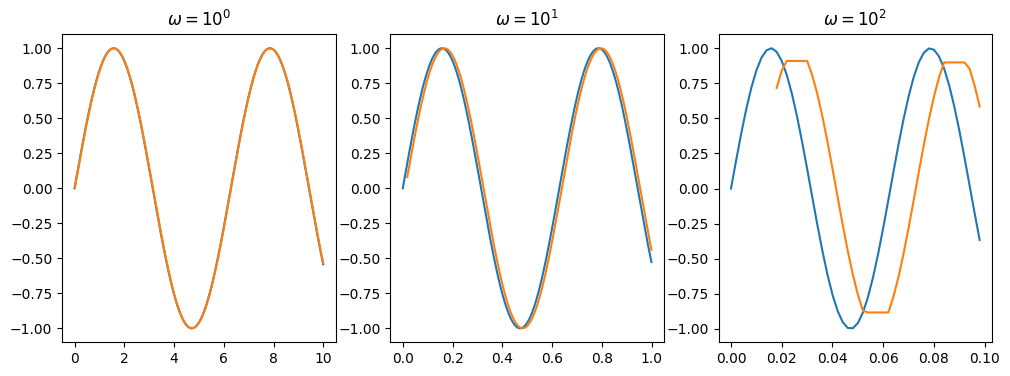
中央値フィルタの応答例


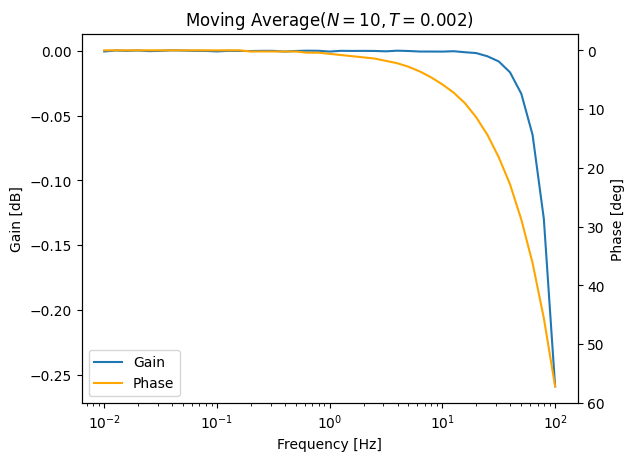
中央値フィルタのボード線図

外れ値除去

移動平均を取る際、範囲から最大値・最小値を除去して平均を求める。

高速フーリエ変換

高速フーリエ変換(Fast Fourier Transform: FFT)を使えば指定の周波数以降の信号をカットできる。
しかし計算量が大きいためリアルタイム処理には使用しにくい。組み込み向きではないと思う。


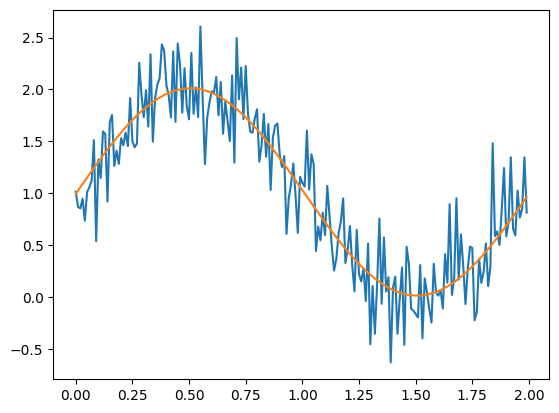
FFTによるノイズ除去の応答例

LPFの例

図1にノイズの乗った信号とLPFを挟んだものの例を示す。
青: 信号(sin波)に正規分布するノイズを付加したもの。
橙: LPFを挟んだもの。
緑: 信号(sin波)の実値との偏差。


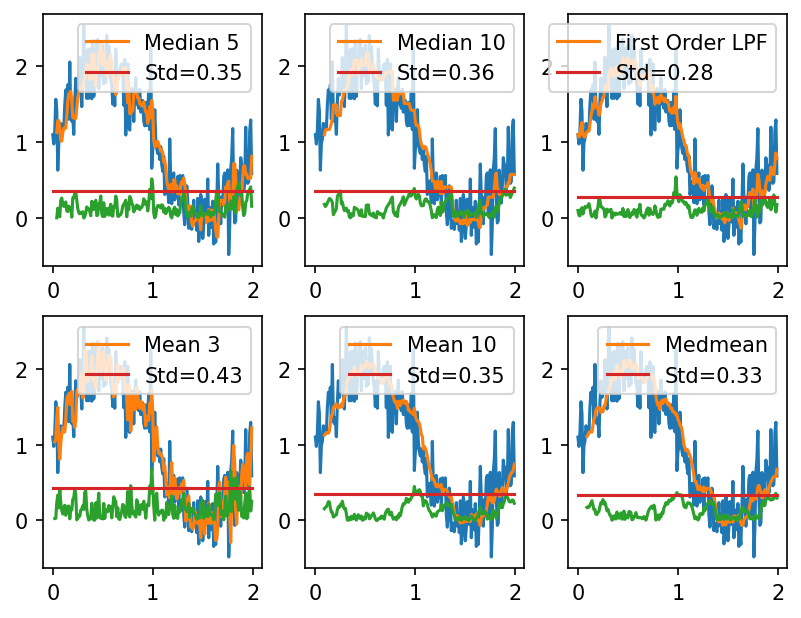
図1 LPFのシミュレーション[7]

脚注

  1. https://ja.wikipedia.org/wiki/ディジタルフィルタ ↩︎

  2. https://qiita.com/yuji0001/items/b0bf121fb8b912c02856 ↩︎

  3. https://ja.wikipedia.org/wiki/畳み込み ↩︎

  4. https://qiita.com/motorcontrolman/items/39d4abc6c4862817e646 ↩︎

  5. https://haizairenmei.com/2018/10/27/arduino_noise/ ↩︎

  6. https://blog.chachay.org/2016/01/moving-average-LPF.html ↩︎

  7. https://github.com/teruyamato0731/pid-simulation ↩︎

このスクラップは2ヶ月前にクローズされました