多重共線性と線形回帰係数推定量の分布
完全な多重共線性がある場合の推定量の分布
が与えられたとき、
ここで、
このとき、最小二乗法による係数
説明変数間に完全な多重共線性がある場合には係数推定値は一意に定まらないが、上記の式(2)は同じ予測値を与える同値な全ての係数推定値を表現できる。
今回は、誤差項が独立同時な正規分布に従うと仮定したうえで、そのような完全な多重共線性がある場合の推定量の分布について見ていく。
結果
誤差項
このとき、式(2)で表された最小二乗推定量
導出
式(2)に式(1)を代入し、
従って、両辺に期待値を取れば式(3)が成り立つ。
次に、共分散行列については、
であるので、
なお、
証明
であり、
これを示すには、
が分かればよい。
よって、
具体例
定数項あり・2変数(
ただし、
ここで、係数を
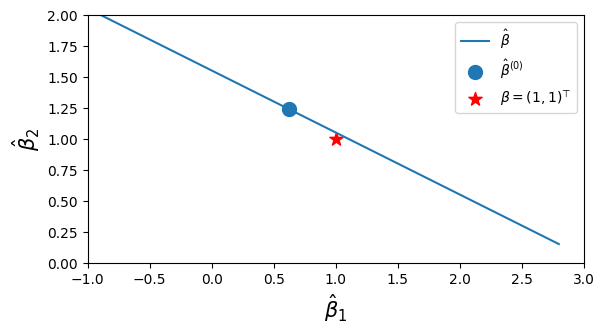
青点が
さらに、説明変数
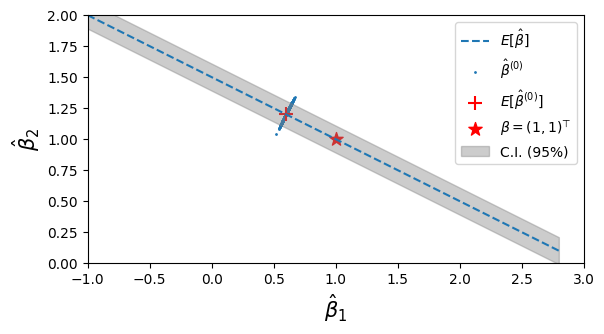
すると、青点で表した推定量
きちんと計算すると、係数推定量
のように表され、これは
このうち
なお、係数の「真の」値
次に推定量の分散を見る。共分散行列は
と表されることから、推定量は
この分散をもとに計算した95%信頼区間を、図で影付きで表した。
計算方法
式(5)、(6)の計算方法について記述する。
このとき残差回帰により、
を用いると、係数
従って、式(3)、(4)に従い、
のように表すことができる。
Moore-Penrse 逆行列 \tilde{\boldsymbol{X}}^+
ここで、
ここで、
であることから固有値
さらに、
以上から、
であり、従ってその Moore-Penrose 逆行列は
のように求まる。
推定量期待値
上記より
であることから、式(7)にこれと
となり、
推定量共分散行列
式(8)に先ほどの
これにより式(6)が求まった。
コード
シミュレーション・作図に用いた Python コードは以下にある:
完全な多重共線性がある場合の Ridge 回帰推定量の分布
(とりあえずグラフだけ貼っておく)
