Zenn
🍗

「Spike-and-Slab事前分布を理解する」補足（Stan による実装ほか）

2024/02/03に公開
統計学
ベイズ統計
ppl
Stan
線形回帰
tech

はじめに

前回公開した下記の記事では、ベイズ推定において予測への寄与に応じて確率的に変数選択を行うために用いられる Spike-and-Slab 事前分布について解説を行い、そのうえで PyMC を用いた類似実装を紹介した。

https://zenn.dev/tatamiya/articles/c8d22acad5294a

本記事では、上記記事に補足する形で下記の3点について記述する。

補足1では、前回の記事で PyMC により実装した（緩やかな）Spike-and-Slab 事前分布を用いた線形回帰について、Stan を用いた書き方を紹介する。

補足2では、CausalImpact で用いられているものと同様な（完全な）Spike-and-Slab 事前分布を用いた線形回帰を、確率的プログラミング言語 (PPL) で実装を試みた結果について紹介する。

補足3では、（完全な）Spike-and-Slab 事前分布による線形回帰を PPL を使わずに Gibbs Sampling を用いて実行した結果を紹介する。

補足に入る前に: この記事でのモデルの呼び分け

Spike-and-Slab 事前分布の最もわかりやすい定式化は、選択変数 \boldsymbol{\rho} を導入して \rho_k = 0 のとき k 番目の説明変数をモデルから除去するというものである。実際、CausalImpact ではこの方法に基づき実装がなされている。
一方で前回の PyMC による実装では、実装を容易にするために選択変数が \rho_k=0 のとき回帰係数 \beta_k の事後分布として 0 を中心とした分散の小さい細長い分布を与えるようにした。
本記事では便宜的に前者を「完全な Spike-and-Slab 事前分布」、後者を「緩やかな Spike-and-Slab 事前分布」と呼び分けることにする。[1]

補足1: 緩やかな Spike-and-Slab 事前分布を用いた線形回帰の Stan 実装

ここでは、前回の記事で PyMC 実装を行ったのと同様な（緩やかな）Spike-and-Slab 事前分布を用いた線形回帰を Stan を用いて実装する。

Stan も PyMC 同様によく使われる確率的プログラミング言語(PPL)だが、PyMC と異なり離散分布をパラメータとして用いることができない。
したがって、変数選択のために導入した Bernoulli 分布に従う変数 \boldsymbol{\rho} をそのまま記述することができない。

そこで、松浦「StanとRでベイズ統計モデリング」の Chapter 11 で混合正規分布やゼロ過剰ポアソン分布を例に解説されている内容を参考に、周辺化による離散変数の消去を行いモデルの記述を行なった。[2]

モデル概要

前回の記事の繰り返しになるため詳細は省くが、モデルを式で表すと以下のようになる（実行に用いた R のコードはこちら）：

\begin{aligned} \boldsymbol{Y} \vert \boldsymbol{\beta}, 1/\sigma^2 &\sim N(\boldsymbol{X} \boldsymbol{\beta}, \sigma^2 \boldsymbol{I}_n),\\ \boldsymbol{\beta} \vert 1/\sigma^2, \boldsymbol{\rho} &\sim N(\boldsymbol{I}_\rho \boldsymbol{b}, \sigma^2 (\tilde{\boldsymbol{\Sigma}}_\rho^{-1})^{-1}),\\ 1/\sigma^2 &\sim {\rm Ga}\left(\frac{\nu}{2}, \frac{s}{2}\right),\\ P(\boldsymbol{\rho}) &= \prod_{k=1}^p \pi_k^{\rho_k} (1 - \pi_k)^{1 - \rho_k} \qquad (0\le\pi_k\le 1). \end{aligned}

記号の定義は前回の記事と同じである。

これのようなモデル設定により、\rho_k=0 に対応する説明変数をモデルから除外するのではなく、回帰係数 \beta_k に 0 付近に局在した（\rho_k=1 の場合と比べると分散の小さい）事前分布を与えている。

モデル実装

上記のモデル設定を Stan で書き表すと以下のようになる（なお、説明変数の数 p は、下記のコードでは D で表している）：

data {
  int N;
  int D;
  matrix[N, D] X;
  vector[N] Y;

  // for out-of-sample prediction
  int N_new;
  matrix[N_new, D] X_new;
}

// The parameters accepted by the model.
parameters {
  vector[D] beta;
  real<lower=0> sigma2;
}

transformed parameters {
  vector[N] mu;
  mu = X*beta;

  real tau = 1/sigma2;
}

// The model to be estimated.
model {
  // parameters for beta prior
  vector[D] beta0;
  array[D] int rho;
  vector[D] rho_v;
  array[D] real rho_pi;
  vector[D] i_D;
  vector[to_int(2^D)] lp;
  for (i in 1:D) {
    beta0[i] = 0;
    rho[i] = 0;
    rho_v[i] = 0;
    rho_pi[i] = 0.5;
    i_D[i] = 1;
  }

  //// variance-covariance matrix
  matrix[D, D] des_mat = X' * X;
  matrix[D, D] beta_prec_full = 0.5 / N * (des_mat + diag_matrix(diagonal(des_mat)));


  // parameters for sigma^2 prior
  real nu = 0.01;
  real r2 = 0.5;
  real sy = variance(Y);
  real s = nu * (1-r2) * sy;

  // model definition
  matrix[D,D] diag_beta_prec = diag_matrix(diagonal(beta_prec_full));
  for (k in 1:to_int(2^D)) {
    matrix[D,D] beta_prec_mat = quad_form_diag(beta_prec_full, rho_v) + N^2 * diag_pre_multiply(i_D - rho_v, diag_beta_prec);

    lp[k] = normal_lpdf(Y | X * beta, sqrt(sigma2)) + multi_normal_lpdf(beta | beta0, sigma2 * inverse(beta_prec_mat))  + inv_gamma_lpdf(sigma2 | nu/2, s/2);

    // P(rho) の対数確率を加算する
    for (i in 1:D) {
      lp[k] += bernoulli_lpmf(rho[i] | rho_pi[i]);
    }

    // ベクトル rho を更新
    int rho_increment = 1;
    for (i in 1:D) {
      int tmp_added = rho[i] + rho_increment;
      if (tmp_added==2) {
        rho[i]=0;
      } else {
        rho[i] = tmp_added;
        rho_increment = 0;
      }
      rho_v[i] = rho[i];
    }
  }
  //print("log_sum_exp(lp): ", log_sum_exp(lp));
  target += log_sum_exp(lp);

}

generated quantities {
  vector[N_new] Y_new;
  vector[N_new] mu_new;

  mu_new = X_new * beta;
  for (n in 1:N_new) {
    Y_new[n] = normal_rng(mu_new[n], sqrt(sigma2));
  }
}

着目するべきは、モデル定義を行う下記の箇所である：

  for (k in 1:to_int(2^D)) {
    matrix[D,D] beta_prec_mat = quad_form_diag(beta_prec_full, rho_v) + N^2 * diag_pre_multiply(i_D - rho_v, diag_beta_prec);

    lp[k] = normal_lpdf(Y | X * beta, sqrt(sigma2)) + multi_normal_lpdf(beta | beta0, sigma2 * inverse(beta_prec_mat))  + inv_gamma_lpdf(sigma2 | nu/2, s/2);

    // P(rho) の対数確率を加算する
    for (i in 1:D) {
      lp[k] += bernoulli_lpmf(rho[i] | rho_pi[i]);
    }

    // ベクトル rho を更新
    // （省略）
  }
  target += log_sum_exp(lp);

ここでは \log P(\boldsymbol{Y}, \boldsymbol{\beta}, 1/\sigma^2) を求めて target に加算しているが、その過程で以下のように同時分布 P(\boldsymbol{Y}, \boldsymbol{\beta}, 1/\sigma^2, \boldsymbol{\rho}) について \boldsymbol{\rho} の取りうる全パターン（2^p 通り）を足し合わせることで周辺化している：

\begin{aligned} P(\boldsymbol{Y}, \boldsymbol{\beta}, 1/\sigma^2) &= \sum_{\boldsymbol{\rho}} P(\boldsymbol{Y}, \boldsymbol{\beta}, 1/\sigma^2, \boldsymbol{\rho})\\ &= \sum_{\boldsymbol{\rho}} P(\boldsymbol{Y} \vert \boldsymbol{\beta}, 1/\sigma^2, \boldsymbol{\rho}) P(\boldsymbol{\beta} \vert 1/\sigma^2, \boldsymbol{\rho}) P(1/\sigma^2) P(\boldsymbol{\rho}). \end{aligned}

今回の実験の場合でいうと p=6 なので、 \boldsymbol{\rho} = (0, 0, 0, 0, 0, 0)^\top \sim (1,1,1,1,1,1)^\top までの全2^6 = 64パターンについて和を取っている。

なお、コード上では配列 lp の各要素に

\begin{aligned} \log P(\boldsymbol{Y}, \boldsymbol{\beta}, 1/\sigma^2, \boldsymbol{\rho}) &= \log P(\boldsymbol{Y} \vert \boldsymbol{\beta}, 1/\sigma^2, \boldsymbol{\rho}) + \log P(\boldsymbol{\beta} \vert 1/\sigma^2, \boldsymbol{\rho}) \\ &\qquad + \log P(1/\sigma^2) + \log P(\boldsymbol{\rho}) \end{aligned}

を代入したうえで、最終的に log_sum_exp(lp) により

\log P(\boldsymbol{Y}, \boldsymbol{\beta}, 1/\sigma^2) = \log \left[ \sum_{\boldsymbol{\rho}} \exp \{ \log P(\boldsymbol{Y}, \boldsymbol{\beta}, 1/\sigma^2, \boldsymbol{\rho})\} \right]

を求めている。

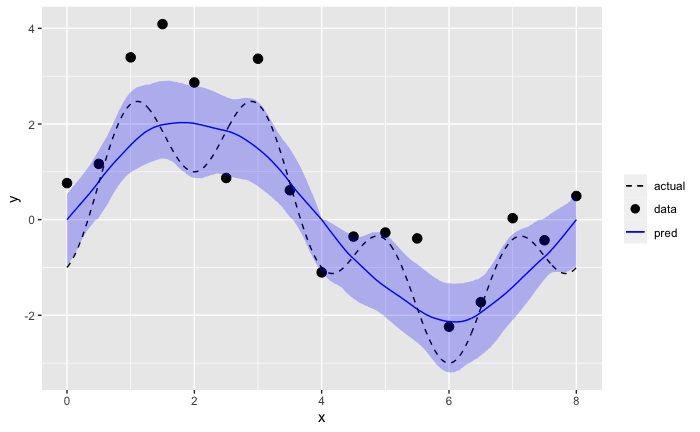
可視化結果

前回 PyMC で実行した結果と大局的には大きな違いがないことを確認した。

事後予測値

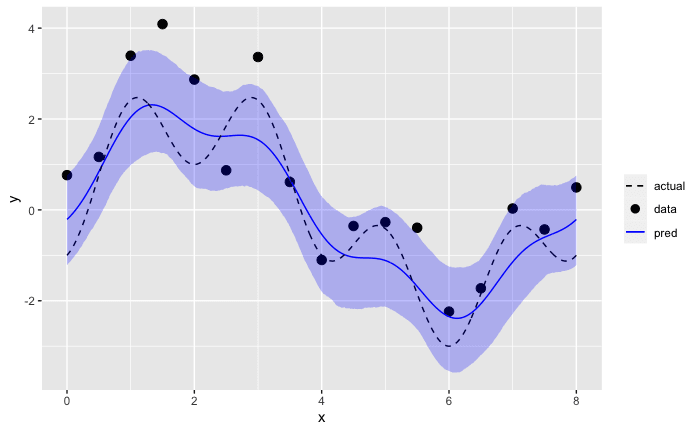
目的変数 Y の予測値 \mu=\boldsymbol{X} \boldsymbol{\beta}（中央値）と95%ベイズ予測区間は以下の通りであった：

これは、PyMC による予測結果と定性的には大きな違いがない。

回帰係数事後分布

次に、回帰係数 \boldsymbol{\beta} = (\beta_1, \beta_2, \beta_3, \beta_4, \beta_5, \beta_6)^\top の事後分布である。
水平の黒線は、細い方は95%、太い方は50% HDI (High Density Interval) である。
赤のマークはサンプルデータ生成時に用いた真の値である。

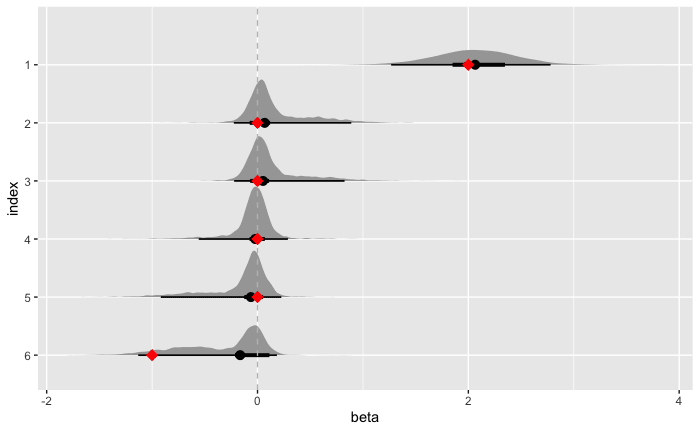
こちらについては PyMC で出力した内容と50%区間の幅など微妙に異なる部分はあるものの、\beta_1 の事後分布は1を中心とし、\beta_2, \beta_3, \beta_4, \beta_5 は 0 付近に集中している点は一致している。

補足2: 完全な Spike-and-Slab 事前分布の実装を PyMC / Stan で実現できるか？

補足1と前回の PyMC 実装では、冒頭で述べた「緩やかな」方の Spike-and-Slab 事前分布を用いた。
それでは「完全な」方の Spike-and-Slab 事前分布を用いた線形回帰についても、PyMC や Stan を用いて実装できるのだろうか？

これについて筆者は試してみたが、現時点ではうまくいっていない。
困難なポイントとして、以下が挙げられる：

  • 確率変数 \boldsymbol{\rho} の値に応じて別の確率変数 \boldsymbol{\beta}_\rho の内容・形状を動的に変化させることがフレームワークの仕様的に難しい
  • MCMC の収束が遅い

以下、試行内容とその結果について軽く触れる。

PyMC による試行

\boldsymbol{\rho} の値に応じて回帰係数を動的に変えることができなかった。

以下のように、選択変数 \boldsymbol{\rho} を表す rho = pm.Bernoulli('rho', .5, shape=p) の値を用いて回帰係数 \boldsymbol{\beta}_\rho に相当する beta_rho を定義してみたが、変数 rho には numpy の array のような形で実際の値が入るわけではないためエラーになった。

n = y.shape[0]
p = X.shape[1]

model = pm.Model()
with model:
    rho = pm.Bernoulli('rho', .5, shape=p)

    p_rho = sum(rho)
    X_rho = X[:, rho==1]
    Sigma_rho = 0.5 * np.matmul(X_rho.T, X_rho) / n
    Sigma_rho += np.diag(np.diag(Sigma_rho))

    beta_rho = pm.MvNormal('beta_rho', 0, tau=tau * Sigma_rho, shape=p_rho)
    # （以降略）

詳細： https://zenn.dev/link/comments/5a121ffe835838

Stan による試行

MCMC の収束が遅く想定していた結果が得られなかった。[3]

以下のメモのように \boldsymbol{\beta} を表すベクトルパラメータ beta を切り出して beta_rho を作りモデルを記述した。

この場合では Stan コードのコンパイルが成功し実行はできたものの、回帰係数の大きさが10^{19}を超えるなど極端な値を取っていた。
収束の目安となる指標 \hat{R} の値は全回帰係数で1.1を大きく上回っており、実際サンプリング軌道や分布をみると chain ごとに大きく異なるものとなっていた。

詳細： https://zenn.dev/link/comments/b68820f6360b9c

補足3: 完全な Spike-and-Slab 事前分布の Gibbs Sampling を用いた実装

そもそもの話ではあるが、今回の設定では完全な Spike-and-Slab 事前分布を用いた線形回帰を確率的プログラミング言語を使わずに実装が可能である。
以下に再掲する前記事の式(1)のように事後分布の関数形が分かるので、これらを利用してサンプリングすればよい：

\begin{aligned} 1/\sigma^2 \vert \boldsymbol{Y}, \boldsymbol{\rho} &\sim {\rm Ga}\left( \frac{n+\nu}{2}, \frac{S_{Y,\rho}}{2}\right),\\ \boldsymbol{\beta}_\rho \vert \boldsymbol{Y},1/\sigma^2, \boldsymbol{\rho} &\sim N(\tilde{\boldsymbol{\beta}}_\rho, \sigma^2 (\boldsymbol{\Omega}_\rho^{-1})^{-1}),\\ P(\boldsymbol{\rho} \vert \boldsymbol{Y}) &= \frac{1}{P(\boldsymbol{Y})} \frac{1}{\pi^{\frac{n}{2}}} \frac{|\boldsymbol{\Sigma}_\rho^{-1}|^{\frac{1}{2}}}{|\boldsymbol{\Omega}_\rho^{-1}|^{\frac{1}{2}}} \frac{\Gamma\left( \frac{n+\nu}{2}\right)}{\Gamma\left( \frac{\nu}{2}\right)} \frac{s^{\frac{\nu}{2}}}{S_{Y,\rho}^{\frac{n+\nu}{2}}} P(\boldsymbol{\rho}). \tag{1} \end{aligned}

ただし、P(\boldsymbol{\rho}\vert \boldsymbol{Y}) については直接サンプリングできないので、Gibbs Sampling を行う（ホフ「標準ベイズ統計学」9.3節参照）。

具体的な実行方法についてはこちらのメモもしくは実行コードを参照いただき、以下に結果だけ掲載する。

選択変数 \boldsymbol{\rho} の事後分布：

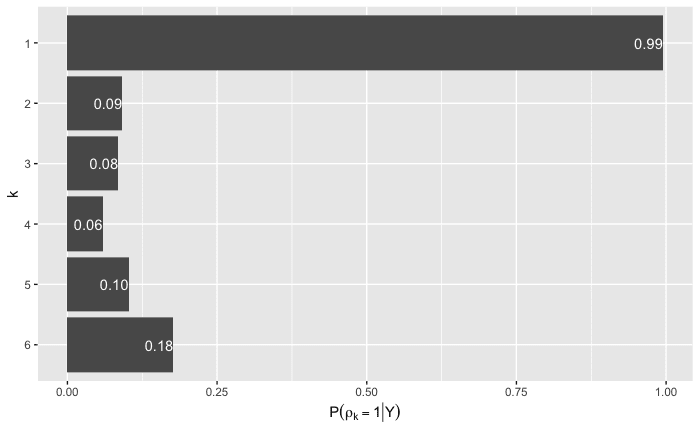
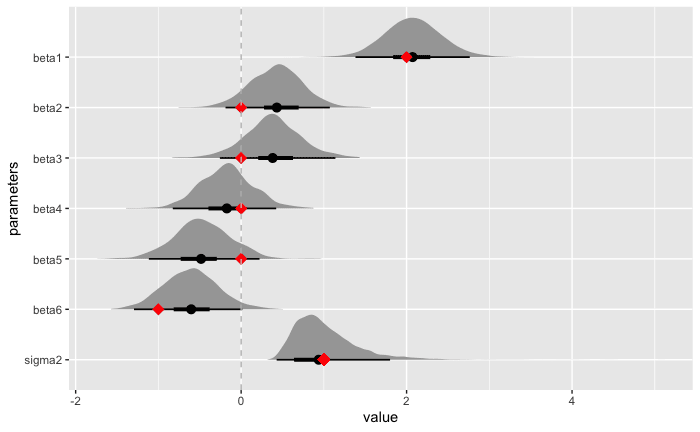
パラメータ \boldsymbol{\beta}, \sigma^2 の事後分布（細線・太線はそれぞれ 95%、50%の信用区間を表す）：

事後予測値 \boldsymbol{X}\boldsymbol{\beta} とその95%区間：

参考文献

https://amzn.asia/d/6WybSkX

https://amzn.asia/d/gwnefwc

脚注

  1. 直感的には、「緩やかな Spike-and-Slab 事前分布」において \rho_k=0 のときの \beta_k の事前分布を極限まで細く（デルタ関数に）したものが、「完全な Spike-and-Slab 事前分布」である。 ↩︎

  2. 本実装は、著者の Matsuura さんからいただいたコメントがきっかけとなりました。改めて感謝申し上げます。 ↩︎

  3. なお、「緩やかな」方の Spike-and-Slab 事前分布の場合でも、\rho_k=0 の際の \beta_k の事前分布の分散を小さくしすぎるとサンプリングの収束が遅くなることがわかっている。 ↩︎

Discussion