Spike-and-Slab 事前分布を理解する
この Scrap は?
確率的プログラミング言語 Advent Calendar 2023 24日目の記事執筆のためのメモ。
CausalImpact で使われている Spike-and-Slab 事前分布について理解した内容をまとめる予定。
やろうとしていること
Spike-and-Slab 事前分布の最低限の事前分布の定義と意味を把握したうえで、同分布を用いた簡単な(時系列でない)回帰モデルを作ってみる。
モデルは、可能であれば Stan あたりの PPL を用いて実装したい。 → Stan では難しいと分かったので、ひとまずは PyMC を用いることにした。
Spike-and-Slab 事前分布とは(現時点での理解)
- 回帰モデルにて変数選択のために導入される事前分布。
- モデル中に、各説明変数をモデルに含めるか含めないかを表す変数を入れる。
- その変数の事前分布はベルヌーイ分布として定義する。
- 予測への寄与が少ない変数ほど選択率(事後確率)が低くなる。
現在できていること
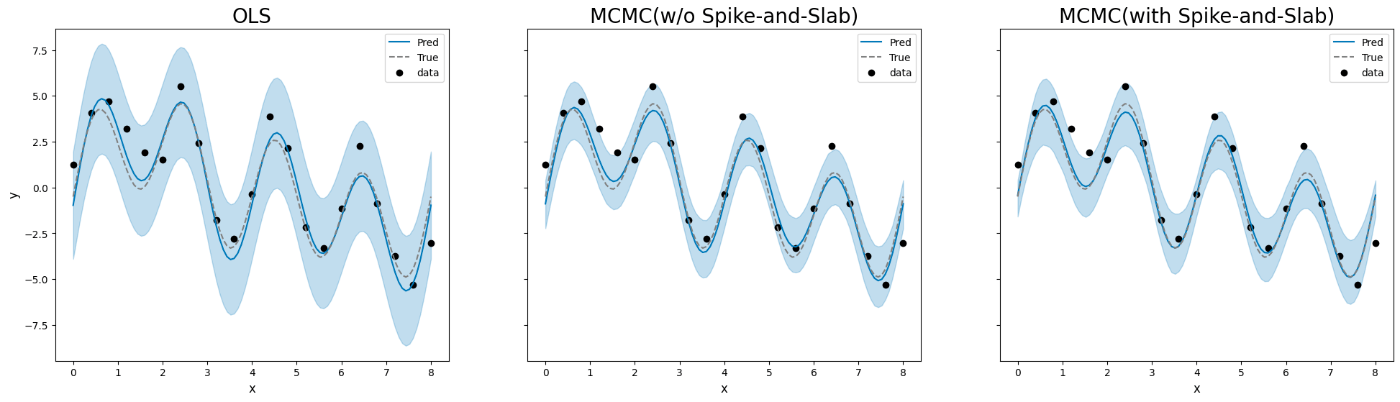
PyMCによる実装を紹介した記事 のコードをそのまま使い、異なる周期のsin波・cos波を重ね合わせたデータに対して Spike-and-Slab 事前分布を用いた線形回帰を試した。
そのうえで、Spike-and-Slab 事前分布を使わないモデル・(MCMC を用いない)OLS によるモデルの結果と比較した。
実験設定
(目的変数)
(説明変数)
...
現時点で出ている結果
- 説明変数として選択されるかを表す変数を調べたところ、入力データで係数0とした説明変数においては事後確率が相対的に低く出た
- 下記の図の
xi[1],xi[5]が該当
- 下記の図の

-
Spike-and-Slab 事前分布を用いた線形回帰では、同事前分布を用いず MCMC を適用した場合や OLS による推定と比べて、推定値の信用区間(注:用語の使い方が合っているか要チェック)が狭くなった。- → (可視化コードの誤りを修正)OLS による推定と比べると、Spike-and-Slab 事前分布を用いた場合の推定区間は OLS における推定区間より幅が狭くなったが、 Spike-and-Slab 事前分布を用いた場合と用いずにMCMCを実行した場合とでは大きな差はみられなかった。
ToDO
-
モデル(特に事前分布)の見直し・再計算
- 参考元の記事の実装は、CausalImpact 論文で紹介されているものと事前分布が異なることがわかったため。
- また、現状の実装方法で事後分布が論文の通りに計算できているかも見直す。
-
Spike-and-Slab 事前分布の理論的説明
- 同事前分布を用いないベイズ重回帰との比較と交えながら解説したい。
- 文章の形にまとめて公開
実行コード
文献
CausalImpact の論文
CausalImpact 論文で引用されている論文
-
- 説明変数が増えた場合の挙動と hierarchical prior との比較の際に言及
そのほか CausalImpact の作成者の一人 Steven L. Scott 氏による文献
そのほか、Spike-and-Slab 事前分布に関連した文献
特徴量選択・スパース推定などの文脈で書かれたものを含む。
Spike-and-Slab 回帰
CausalImpact の作者でもある Steven L. Scott さんによる Spike-and-Slab 回帰のパッケージ → 試そうとしたが、インストールに失敗した。
Stan による実装?
http://www.batisengul.co.uk/post/spike-and-slab-bayesian-linear-regression-with-variable-selection/#:~:text=Spike and slab is a,from the regression towards zero.
→ Stan じゃ離散分布扱えないからと、最終的に PyMC を使っている。
Horseshoe 分布
Stan などでは離散分布が扱いにくいのでそれに近い連続分布として Horseshoe 分布なるものが使われることもあるらしい。
NumPyro 実装
PPL における離散分布の扱い
PyMC 以外にも、NumPyro でも離散分布を扱えるらしい。
まずは既存パッケージ BoomSpikeSlab を試してみようとしたら、ビルドがこけた
install.packages("BoomSpikeSlab")
also installing the dependency ‘Boom’
trying URL 'https://cran.ism.ac.jp/src/contrib/Boom_0.9.13.tar.gz'
Content type 'application/x-gzip' length 2507784 bytes (2.4 MB)
==================================================
downloaded 2.4 MB
trying URL 'https://cran.ism.ac.jp/src/contrib/BoomSpikeSlab_1.2.6.tar.gz'
Content type 'application/x-gzip' length 129203 bytes (126 KB)
==================================================
downloaded 126 KB
* installing *source* package ‘Boom’ ...
** package ‘Boom’ successfully unpacked and MD5 sums checked
** using staged installation
** libs
using C++ compiler: ‘Apple clang version 14.0.0 (clang-1400.0.29.202)’
using C++17
using SDK: ‘MacOSX13.1.sdk’
(中略)
strip --strip-debug libboom.a
error: /Library/Developer/CommandLineTools/usr/bin/strip: unrecognized option: --strip-debug
Usage: /Library/Developer/CommandLineTools/usr/bin/strip [-AnuSXx] [-] [-d filename] [-s filename] [-R filename] [-o output] file [...]
make: *** [libboom.a] Error 1
ERROR: compilation failed for package ‘Boom’
* removing ‘/usr/local/Cellar/r/4.3.1/lib/R/library/Boom’
Warning in install.packages :
installation of package ‘Boom’ had non-zero exit status
ERROR: dependency ‘Boom’ is not available for package ‘BoomSpikeSlab’
* removing ‘/usr/local/Cellar/r/4.3.1/lib/R/library/BoomSpikeSlab’
Warning in install.packages :
installation of package ‘BoomSpikeSlab’ had non-zero exit status
The downloaded source packages are in
‘/private/var/folders/js/n4rh779x3gd78qnzrpf58b540000gn/T/Rtmp5BeJFq/downloaded_packages’
Updating HTML index of packages in '.Library'
Making 'packages.html' ... done
以下のエラーメッセージで Google 検索してみたが、よくわからなかった。
error: /Library/Developer/CommandLineTools/usr/bin/strip: unrecognized option: --strip-debug
関連がありそうなもので、この辺り?
もう少し絞って、Boom のコンパイルでエラーとのことで以下のメッセージで検索
ERROR: compilation failed for package ‘Boom’
CausalImpact インストール時のエラーがいくつか報告されていた。
(が、CausalImpact 自体はきちんと入っている。)
→ 一旦あきらめる
PyMC で動かしてみる
とりあえず下記の記事の実装をそのまま使って動かしてみた
import pymc3 as pm
import numpy as np
def get_model(y, X):
model = pm.Model()
Sigma = .5 * np.matmul(X.T, X)
Sigma += np.diag(np.diag(Sigma))
Sigma = np.linalg.inv(Sigma)
with model:
xi = pm.Bernoulli('xi', .5, shape=X.shape[1])
tau = pm.HalfCauchy('tau', 1)
sigma = pm.HalfNormal('sigma', 10)
beta = pm.MvNormal('beta', 0, tau * Sigma, shape=X.shape[1])
mean = pm.math.dot(X, xi * beta)
y_obs = pm.Normal('y_obs', mean, sigma, observed=y)
return model

使用データ
目的変数
sin, cos の重ね合わせにランダムノイズを加えたもの
sigma = 1.0
sigma2 = sigma **2
def target_func(x):
return 2 * np.sin(2 * np.pi / 8 * x) + 1 * np.sin(2 * 2 * np.pi / 8 * x) - 0.5 * np.cos(2 * 2 * np.pi / 8 * x) + 3 * np.sin(4 * 2 * np.pi / 8 * x)
y = target_func(x) + sigma * np.random.randn(x.shape[0])
x_sample = x_min + (x_max - x_min) * np.arange(0, 101, 1) / 100
y_org_sample = target_func(x_sample)
fig, ax = plt.subplots()
ax.plot(x_sample, y_org_sample, color="gray", linestyle="dashed")
ax.scatter(x, y)

説明変数
x_des = np.array([np.sin(2 * np.pi / 8 * x), np.cos(2 * np.pi / 8 * x), np.sin(2 * 2 * np.pi / 8 * x), np.cos(2 * 2 * np.pi / 8 * x), np.sin(4 * 2 * np.pi / 8 * x), np.cos(4 * 2 * np.pi / 8 * x)]).T
結果
model = get_model(y, x_des)
with model:
# draw 1000 posterior samples
idata = pm.sample()
パラメータ事後分布
import arviz as az
az.plot_posterior(idata, show=True);

az.plot_forest(idata, var_names=["beta", "sigma"], combined=True, hdi_prob=0.95, r_hat=True);
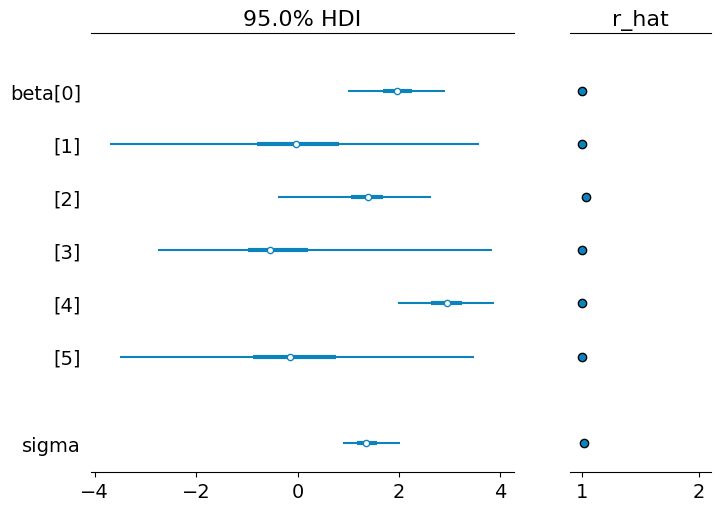
推定結果
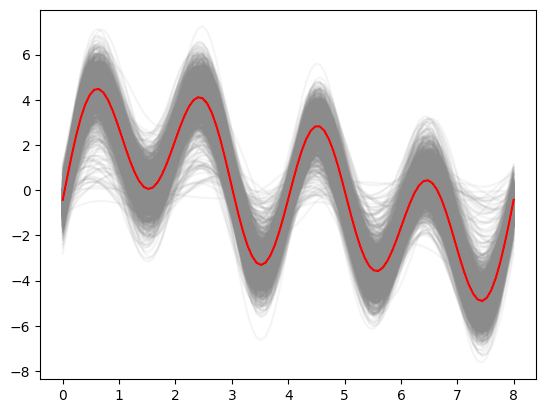

気になること
- spike-and-slab 事前分布を使わない場合と比べるとどうか?
- → 試した。ただし、モデルは見直しが必要(特に事前分布、後述)。
- https://zenn.dev/link/comments/bcfb5c39bb26fc
- 素朴な最小二乗法で推定した結果と比べるとどうか?
- 使用したコードは CausalImpact 論文で解説されている内容に沿った実装がなされているか?
- → されていなさそう。事前分布が異なる。
- 加えて、事後分布の計算方法も気になる箇所があるので要チェック。
Spike-and-Slab 事前分布を使わない通常のベイズ線形回帰の場合
95%信用区間(用語の使い方、正しい?)が Spike-and-Slab 事前分布使った時と比べて広い。
→ Spike-and-Slab 事前分布を用いた場合とほとんど変わりがなかった(可視化コードにミスがあり、修正を加えた)。
モデル
def get_linear_model(y, X):
model = pm.Model()
Sigma = .5 * np.matmul(X.T, X)
Sigma += np.diag(np.diag(Sigma))
Sigma = np.linalg.inv(Sigma)
with model:
#xi = pm.Bernoulli('xi', .5, shape=X.shape[1])
tau = pm.HalfCauchy('tau', 1)
sigma = pm.HalfNormal('sigma', 10)
beta = pm.MvNormal('beta', 0, tau * Sigma, shape=X.shape[1])
#mean = pm.math.dot(X, xi * beta)
mean = pm.math.dot(X, beta)
y_obs = pm.Normal('y_obs', mean, sigma, observed=y)
return model

結果
linear_model = get_linear_model(y, x_des)
with linear_model:
# draw 1000 posterior samples
idata_linear = pm.sample()
パラメータ事後分布
az.plot_posterior(idata_linear, show=True);
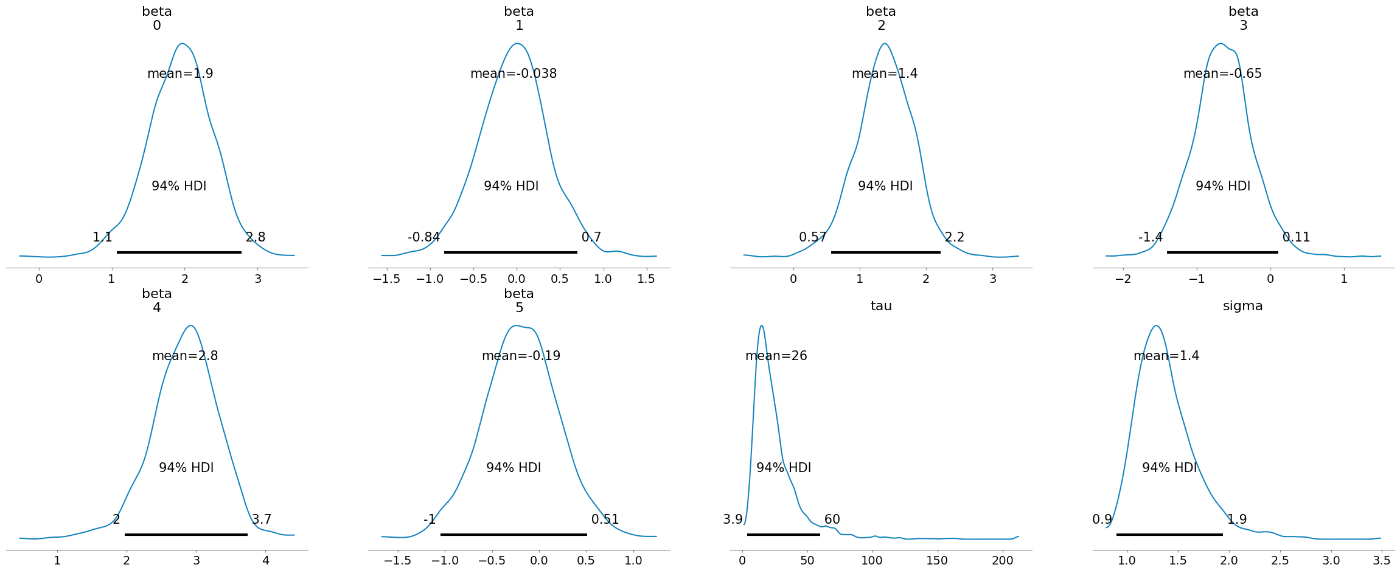
az.plot_forest(idata_linear, var_names=["beta", "sigma"], combined=True, hdi_prob=0.95, r_hat=True);
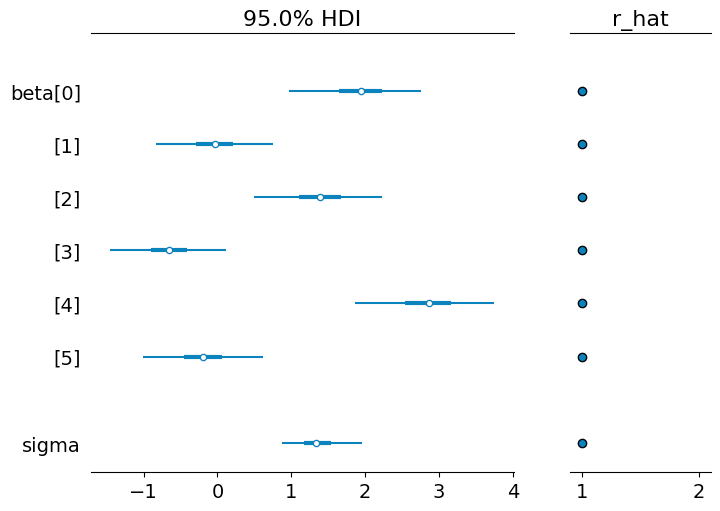
推定結果
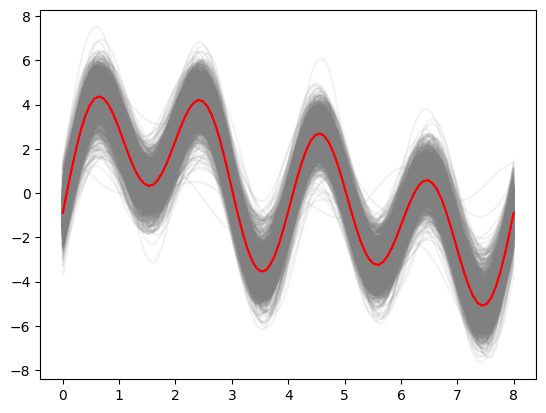
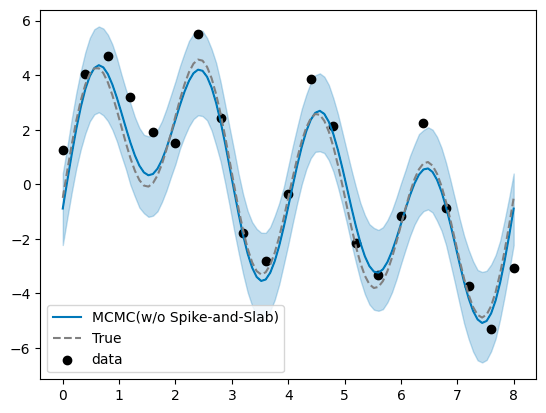
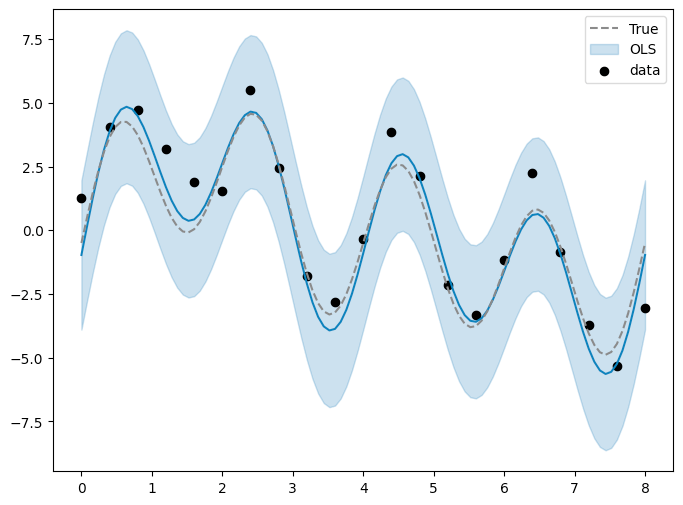
ベイズを使わずに最小二乗法で推定してみる
statsmoldels を使用。
結果、95%信頼区間は、MCMCの Spike-and-Slab 事前分布なしよりは狭いが、Spike-and-Slab 事前分布ありよりは広い、といった具合。
import statsmodels.api as sm
mod = sm.OLS(y, x_des)
res = mod.fit()
print(res.summary())
OLS Regression Results
=======================================================================================
Dep. Variable: y R-squared (uncentered): 0.884
Model: OLS Adj. R-squared (uncentered): 0.837
Method: Least Squares F-statistic: 19.01
Date: Fri, 22 Dec 2023 Prob (F-statistic): 3.18e-06
Time: 14:28:50 Log-Likelihood: -30.769
No. Observations: 21 AIC: 73.54
Df Residuals: 15 BIC: 79.80
Df Model: 6
Covariance Type: nonrobust
==============================================================================
coef std err t P>|t| [0.025 0.975]
------------------------------------------------------------------------------
x1 2.1232 0.392 5.418 0.000 1.288 2.958
x2 -0.0333 0.376 -0.089 0.931 -0.836 0.769
x3 1.5314 0.392 3.908 0.001 0.696 2.367
x4 -0.7255 0.376 -1.927 0.073 -1.528 0.077
x5 3.1613 0.392 8.067 0.000 2.326 3.997
x6 -0.2113 0.376 -0.561 0.583 -1.014 0.591
==============================================================================
Omnibus: 3.294 Durbin-Watson: 1.337
Prob(Omnibus): 0.193 Jarque-Bera (JB): 1.560
Skew: -0.568 Prob(JB): 0.458
Kurtosis: 3.701 Cond. No. 1.14
==============================================================================
Notes:
[1] R² is computed without centering (uncentered) since the model does not contain a constant.
[2] Standard Errors assume that the covariance matrix of the errors is correctly specified.
pred_ols = res.get_prediction(exog=x_sample_des)
iv_l = pred_ols.summary_frame()["obs_ci_lower"]
iv_u = pred_ols.summary_frame()["obs_ci_upper"]
fig, ax = plt.subplots(figsize=(8, 6))
ax.plot(x_sample, pred_ols.predicted);
ax.plot(x_sample, y_org_sample, color="gray", linestyle="dashed", label="True")
ax.fill_between(x_sample, iv_l, iv_u, alpha=0.25, color='tab:blue', label="OLS")
ax.scatter(x, y, label="data", color="black")
ax.legend(loc="best")
Zero-Inflated ガウス分布に相当していると理解しました。Stanでも実装できると思いますよ。詳しくはStanのマニュアルの「Discrete Parameter」の章や『StanとRでベイズ統計モデリング』の11章を参照してください。
コメントありがとうございます!
Stan でも離散分布を用いたモデルを実装できるのですね、確認&試してみます!
Zero-Infrated ガウス分布、初めて知りました。
こちらも並行して調べてみます!
Stan版への準備その1: ベイズ線形回帰
コードはこちら。
Spike-and-Slab 事前分布を用いた線形回帰モデルを Stan で書いてみる前に、同事前分布を用いずにベイズ推定で線形回帰を行い、PyMC での結果と比較してみた。
Stan によるモデルの記述
data {
int N;
int D;
matrix[N, D] X;
vector[N] Y;
// for out-of-sample prediction
int N_new;
matrix[N_new, D] X_new;
}
parameters {
vector[D] beta;
real<lower=0> sigma2;
}
transformed parameters {
vector[N] mu;
mu = X*beta;
}
model {
// parameters for beta prior
//// expected values
vector[D] beta0;
for (i in 1:D) {
beta0[i] = 0;
}
//// variance-covariance matrix
matrix[D, D] des_mat = X' * X;
matrix[D, D] beta_cov = inverse(0.5 / N * (des_mat + diag_matrix(diagonal(des_mat))));
// parameters for tau prior
real nu = 0.01;
real r2 = 0.5;
real sy = variance(Y);
real s = nu * (1-r2) * sy;
// model definition
//// priors
sigma2 ~ inv_gamma(nu/2, s/2);
beta ~ multi_normal(beta0, sigma2 * beta_cov);
//// target var
Y ~ normal(mu, sqrt(sigma2));
}
generated quantities {
vector[N_new] Y_new;
vector[N_new] mu_new;
mu_new = X_new * beta;
for (n in 1:N_new) {
Y_new[n] = normal_rng(mu_new[n], sqrt(sigma2));
}
}
事後分布
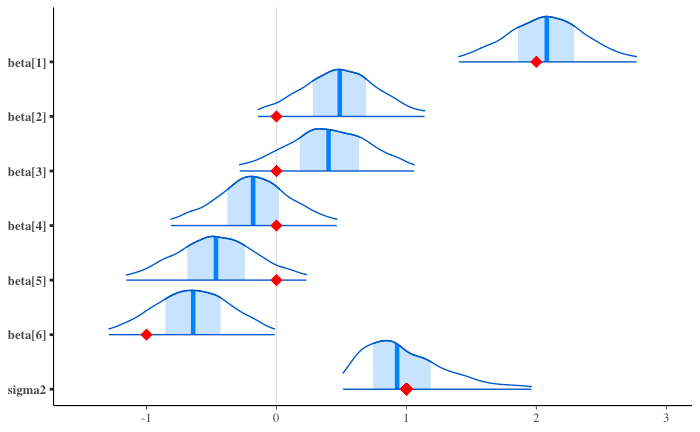
事後予測
薄い青線が事後予測地、濃い青線が真値。

PyMC で行った結果 と(濃淡が逆で見にくいものの)定性的には似ている。

Stan版への準備その2: 緩やかな Spike-and-Slab 事前分布を用いた線形回帰
以前 PyMC を用いて実装した ように、選択されなかった説明変数を完全にはモデルから取り除かず代わりに回帰係数に 0 付近に局在した分布を与えるようにした。
(ここではこのような設定の事前分布を「緩やかな Spike-and-Slab 事前分布」ないし「weak Spike-and-Slab 事前分布」と仮に呼ぶことにする)
実行コードはこちら。
Stan による実装
Stan では離散確率変数をパラメータとして使用できないため、
かわりに、こちらのコメント でいただいた指摘をもとに、周辺化によるパラメータ消去をおこなった。
今回の場合は
なお、今回のモデルでは
data {
int N;
int D;
matrix[N, D] X;
vector[N] Y;
// for out-of-sample prediction
int N_new;
matrix[N_new, D] X_new;
}
parameters {
vector[D] beta;
real<lower=0> sigma2;
vector<lower=0, upper=1>[D] rho_pi;
}
transformed parameters {
vector[N] mu;
mu = X*beta;
}
model {
// parameters for beta prior
vector[D] beta0;
array[D] int rho;
vector[D] rho_v;
vector[D] i_D;
vector[to_int(2^D)] lp;
for (i in 1:D) {
beta0[i] = 0;
rho[i] = 0;
rho_v[i] = 0;
i_D[i] = 1;
}
//// variance-covariance matrix
matrix[D, D] des_mat = X' * X;
matrix[D, D] beta_prec_full = 0.5 / N * (des_mat + diag_matrix(diagonal(des_mat)));
// parameters for sigma^2 prior
real nu = 0.01;
real r2 = 0.5;
real sy = variance(Y);
real s = nu * (1-r2) * sy;
// model definition
matrix[D,D] diag_beta_prec = diag_matrix(diagonal(beta_prec_full));
for (k in 1:to_int(2^D)) {
matrix[D,D] beta_prec_mat = quad_form_diag(beta_prec_full, rho_v) + N^2 * diag_pre_multiply(i_D - rho_v, diag_beta_prec);
lp[k] = normal_lpdf(Y | X * beta, sqrt(sigma2)) + multi_normal_lpdf(beta | beta0, sigma2 * inverse(beta_prec_mat)) + inv_gamma_lpdf(sigma2 | nu/2, s/2);
// P(rho) の対数尤度を加算する
for (i in 1:D) {
lp[k] += bernoulli_lpmf(rho[i] | rho_pi[i]);
}
// ベクトル rho を更新
int rho_increment = 1;
for (i in 1:D) {
int tmp_added = rho[i] + rho_increment;
if (tmp_added==2) {
rho[i]=0;
} else {
rho[i] = tmp_added;
rho_increment = 0;
}
rho_v[i] = rho[i];
}
}
//print("log_sum_exp(lp): ", log_sum_exp(lp));
target += log_sum_exp(lp);
}
generated quantities {
vector[N_new] Y_new;
vector[N_new] mu_new;
mu_new = X_new * beta;
for (n in 1:N_new) {
Y_new[n] = normal_rng(mu_new[n], sqrt(sigma2));
}
}
事後分布
パラメータの事後分布
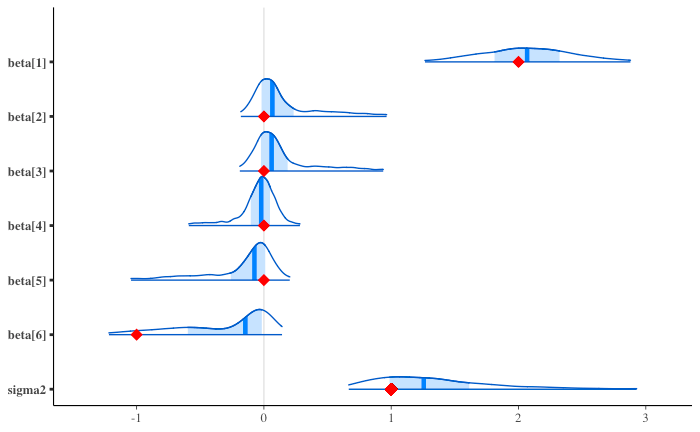
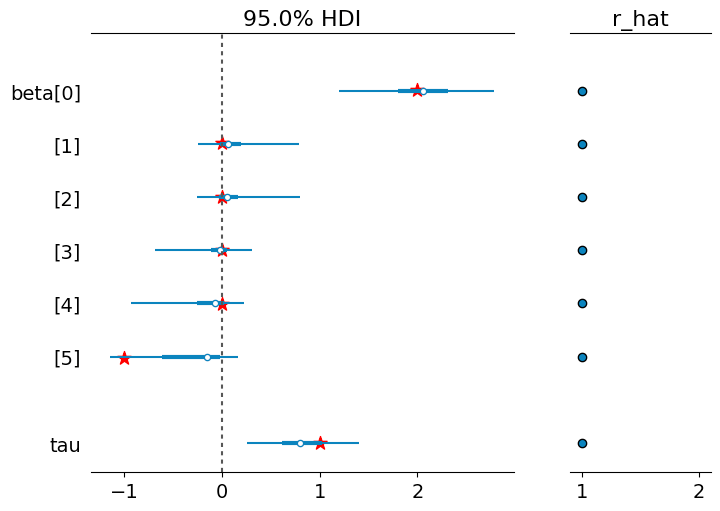
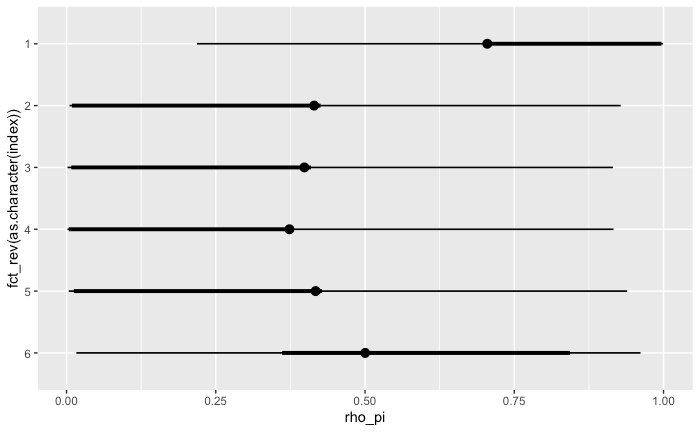
回帰係数の 95% HDI
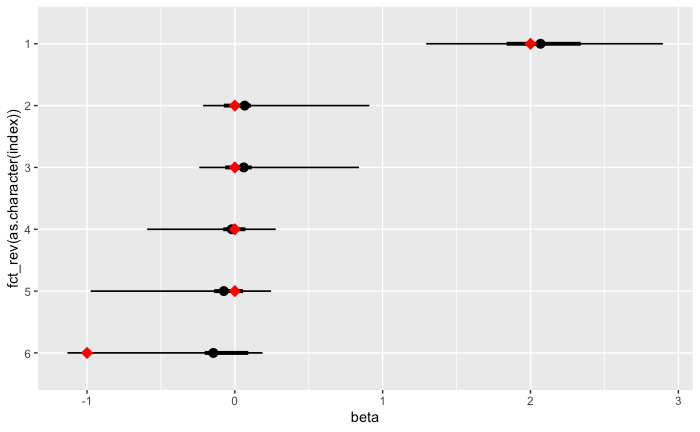
PyMC でおこなった結果 と比べると、細部は異なるが傾向としては似ている。
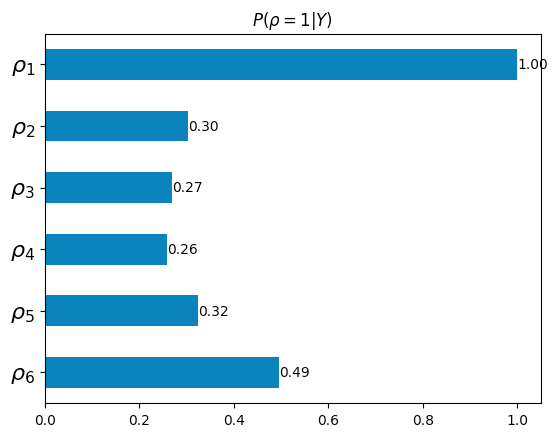
変数選択事後確率
今回の場合、
PyMC で実行した際に計算した
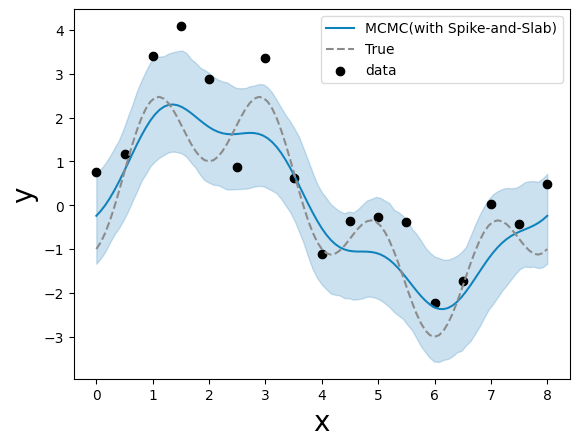
事後予測
薄い青線が事後予測地、濃い青線が真値。
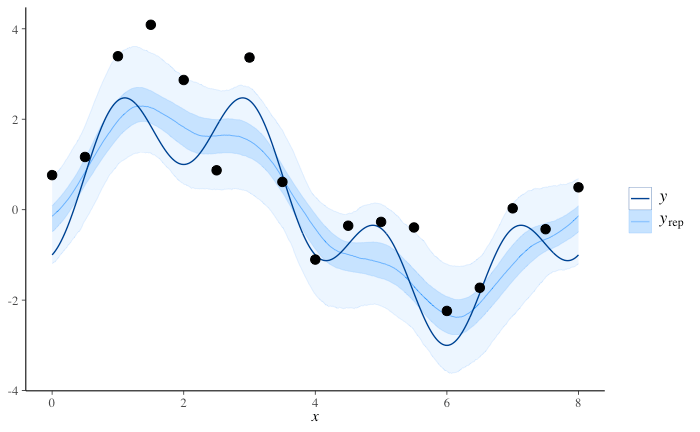
PyMC で行った結果 と(濃淡が逆で見にくいものの)定性的には似ている。
Stan で Spike-and-Slab 事前分布を用いた線形回帰を実装できるか?
CausalImpact で使われているように
これまでの実装と異なり回帰係数
モデル定義
モデルの定義部分を大まかに書くと以下のようになると考えられる:
model {
// パラメータ・定数の定義
// (省略)
// モデル定義
matrix[D,D] diag_beta_prec = diag_matrix(diagonal(beta_prec_full));
for (k in 1:to_int(2^D)) {
// rho[k]=1 に対応する成分のみ抜き出した beta_rho を定義する
beta_rho = ;
b0_rho = ;
beta_cov_rho = ;
// 計画行列 X から rho[k]=1 に対応する列だけ取り出した X_rho を定義する
X_rho = ;
// Y|beta,sigma2,rho の対数尤度を定義
lp[k] = normal_lpdf(Y | X_rho * beta_rho, sqrt(sigma2)) + multi_normal_lpdf(beta_rho | b0_rho, sigma2 * beta_cov_rho) + inv_gamma_lpdf(sgma2 | nu/2, s/2);
// P(rho) の対数尤度を加算する
for (i in 1:D) {
lp[k] += bernoulli_lpmf(rho[i] | rho_pi[i]);
}
// ベクトル rho を更新
// (省略)
}
target += log_sum_exp(lp);
}
上記のうち、特に beta から rho[k] の値が1となる成分だけを取り出して、動的に長さの変わるパラメータ beta_rho (
事後予測
事後予測については以下のようなコードになることが想定される:
generated quantities {
vector[N_new] Y_new;
vector[N_new] mu_new;
array[D] int rho_new;
for (i in 1:D) {
rho_new[i] = bernoulli_rng(rho_pi[i]);
}
X_new_rho = ; // X_new から rho_new[k]=1 に対応する列を抜き出す
beta_rho = ; // P(beta_rho | rho_new, Y, sigma2) からサンプリングする
mu_new = X_new_rho * beta_rho;
for (n in 1:N_new) {
Y_new[n] = normal_rng(mu_new[n], sqrt(sigma2));
}
}
ここでも beta_rho をどうサンプリングするかが問題になる。
一見
しかし、それでは本来欲しかった
実際、両サンプリング方法で事後分布が変わってしまうように見える:
-
P(\boldsymbol{\beta} \vert \boldsymbol{Y}) \boldsymbol{\beta}
-
P(\boldsymbol{\beta}_\rho \vert \boldsymbol{Y}, \boldsymbol{\rho}) \boldsymbol{\beta}_\rho
Stan による Spike-and-Slab 回帰の実装試行その1
以下の spike_and_slab_regression_lpdf() で定義したように、beta から rho[k]=1 となる要素だけ抜き出して beta_rho を定義しモデルを作成した。
しかし、うまくいかなかった。
beta の事後サンプリング値が
(beta_rho に beta の値を入れる時、参照渡しになっていないことが原因?それにしてはbeta[1] は二峰になっているからモデルの構造を何かしら反映していそう。)
→ 参照渡しか値渡しかは関係ないと考えられる(参考)。
MCMC が収束しなかったものと考えられる。
functions {
matrix generate_beta_cov_matrix(matrix X){
int N = dims(X)[1];
int D = dims(X)[2];
matrix[D, D] des_mat = X' * X;
return inverse(0.5 / N * (des_mat + diag_matrix(diagonal(des_mat))));
}
real spike_and_slab_regression_lpdf(vector Y, matrix X, vector beta, real sigma2, real nu, real s, array[] int rho, vector rho_pi){
int D_rho = sum(rho);
vector[D_rho] beta_rho;
vector[D_rho] b0_rho;
int D = size(rho);
int N = size(Y);
matrix[N, D_rho] X_rho;
real lp_Y_cond;
real lp_beta_cond;
real lp_sigma2;
if (D_rho == 0) {
// rho_k が全て0の時だけ特別扱い
lp_Y_cond = normal_lpdf(Y | 0, sqrt(sigma2));
lp_beta_cond = 0;
lp_sigma2 = inv_gamma_lpdf(sigma2 | nu/2, s/2);
} else {
for (k in 1:D_rho){
b0_rho[k] = 0;
}
int beta_index = 1;
for (k in 1:D){
if(rho[k] == 1){
// rho_k=1 となるk要素だけ抜き出した beta_rho を定義する
beta_rho[beta_index] = beta[k];
// 計画行列 X のうち rho_k=1 となる行・列から構成される主部分行列 X_rho を定義する
X_rho[,beta_index] = col(X, k);
beta_index += 1;
}
}
matrix[D_rho, D_rho] beta_cov_rho = generate_beta_cov_matrix(X_rho);
lp_Y_cond = normal_lpdf(Y | X_rho * beta_rho, sqrt(sigma2));
lp_beta_cond = multi_normal_lpdf(beta_rho | b0_rho, sigma2 * beta_cov_rho);
lp_sigma2 = inv_gamma_lpdf(sigma2 | nu/2, s/2);
}
real lp_rho = 0;
for (i in 1:D) {
lp_rho += bernoulli_lpmf(rho[i] | rho_pi[i]);
}
return lp_Y_cond + lp_beta_cond + lp_sigma2 + lp_rho;
}
}
// The input data is a vector 'y' of length 'N'.
data {
int N;
int D;
matrix[N, D] X;
vector[N] Y;
// for out-of-sample prediction
int N_new;
matrix[N_new, D] X_new;
}
// The parameters accepted by the model. Our model
// accepts two parameters 'mu' and 'sigma'.
parameters {
vector[D] beta;
real<lower=0> sigma2;
vector<lower=0, upper=1>[D] rho_pi;
}
transformed parameters {
vector[N] mu;
mu = X*beta;
real tau = 1/sigma2;
}
// The model to be estimated. We model the output
// 'y' to be normally distributed with mean 'mu'
// and standard deviation 'sigma'.
model {
vector[to_int(2^D)] lp;
array[D] int rho;
for (i in 1:D) {
rho[i] = 0;
}
// parameters for sigma^2 prior
real nu = 0.01;
real r2 = 0.5;
real sy = variance(Y);
real s = nu * (1-r2) * sy;
// model definition
// rho=(0,0,...,0) ~ (1,1,...,1) までの全パターンで対数尤度を計算する
for (k in 1:to_int(2^D)) {
// Y|beta,sigma2,rho の対数尤度を定義
lp[k] = spike_and_slab_regression_lpdf(Y | X, beta, sigma2, nu, s, rho, rho_pi);
// ベクトル rho を更新
int rho_increment = 1;
for (i in 1:D) {
int tmp_added = rho[i] + rho_increment;
if (tmp_added==2) {
rho[i]=0;
} else {
rho[i] = tmp_added;
rho_increment = 0;
}
}
}
//print("log_sum_exp(lp): ", log_sum_exp(lp));
target += log_sum_exp(lp);
}
// TODO: 事後予測
//generated quantities {
// vector[N_new] Y_new;
// vector[N_new] mu_new;
// array[D] real rho_pi_new;
//
// for (i in 1:D) {
// rho_pi_new[i] = bernoulli_rng(rho_pi[i]);
// }
//
// X_new_rho = ; # X_new から rho_k=1 に対応する列を抜き出す
// beta_rho = ; # P(beta_rho | rho, Y, sigma2) からサンプリングする
//
// mu_new = X_new_rho * beta_rho;
// for (n in 1:N_new) {
// Y_new[n] = normal_rng(mu_new[n], sqrt(sigma2));
// }
//}
収束の確認
指標
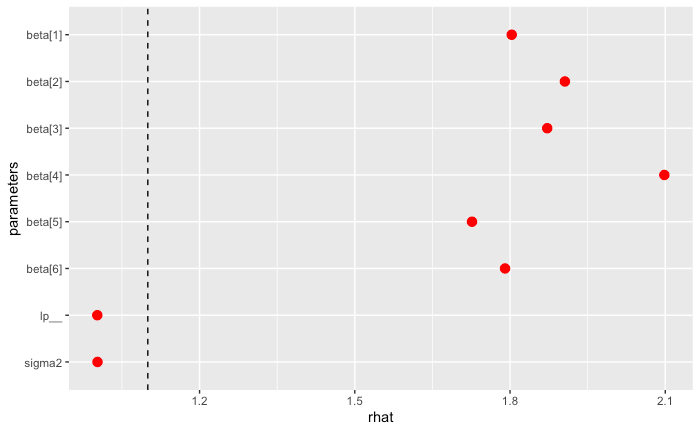
Trace plot を見ても、収束しているように見えないことに加え、chain によっても動きが大きく異なっている。
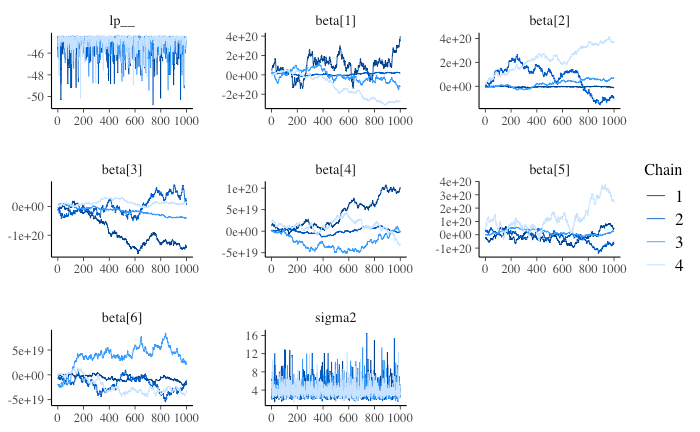
分布も特に回帰係数 beta について chain により大きく異なっている。
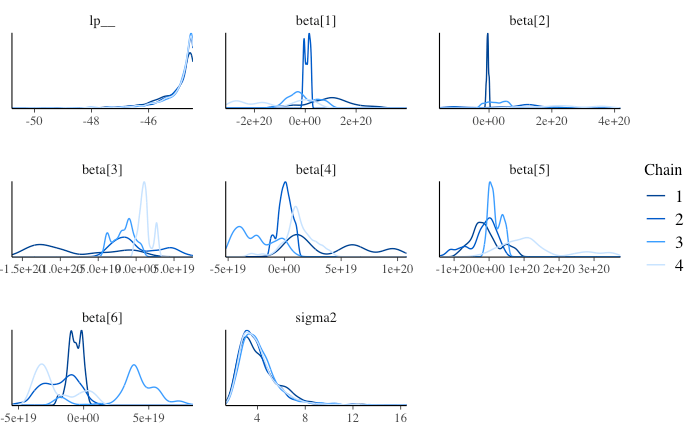
事後予測についての課題
仮にうまくいっていたとしても、事後予測に課題が残る。
上記の方法で自分の想定通り実行できた場合、beta の事後サンプリングは
一方、得たい回帰係数は、事後分布
したがって、
という関係式をもとに
実行コード
Stan による Spike-and-Slab 回帰の実装試行その2
前回は parameters で定義した betaを適宜切り出して beta_rho を作成していたが、今度は始めから
parametesr ブロックで定義した beta_rhos という array がそれである。
// The parameters accepted by the model.
parameters {
real<lower=0> sigma2;
vector<lower=0, upper=1>[D] rho_pi;
array[to_int(2^D)] vector[D] beta_rhos;
}
この方法でもうまくいかなかった。
前回と同様、回帰係数の事後サンプリング値がとてつもなく大きな値をとっていた。
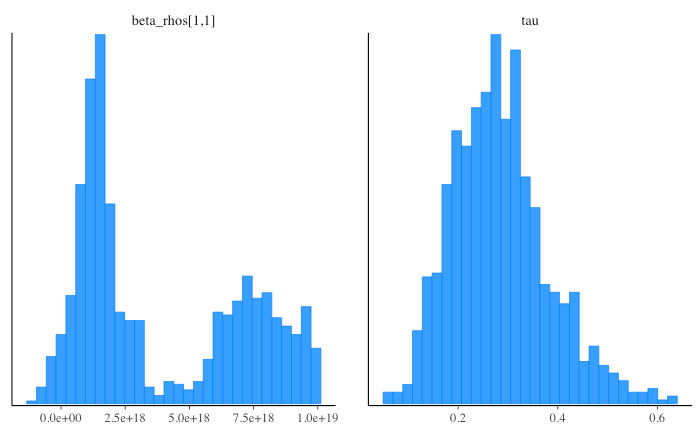
下記のようにモデル定義部分で beta_rho のスライスをおこなっているが、ここが参照ではなく値渡しになっているため、というのが原因としてあり得そうである。
→ 参照渡しか値渡しかは関係ないと考えられる(参考)。
lp_Y_cond = normal_lpdf(Y | X_rho * beta_rho[1:D_rho], sqrt(sigma2));
lp_beta_cond = multi_normal_lpdf(beta_rho[1:D_rho] | b0_rho, sigma2 * beta_cov_rho);
(array beta_rhos を定義する際に各要素を長さの異なる vector にするにはどうすればいいだろう?)
Stan コード全体
functions {
matrix generate_beta_cov_matrix(matrix X){
int N = dims(X)[1];
int D = dims(X)[2];
matrix[D, D] des_mat = X' * X;
return inverse(0.5 / N * (des_mat + diag_matrix(diagonal(des_mat))));
}
real spike_and_slab_regression_lpdf(vector Y, matrix X, vector beta_rho, real sigma2, real nu, real s, array[] int rho, vector rho_pi){
int D_rho = sum(rho);
vector[D_rho] b0_rho;
int D = size(rho);
int N = size(Y);
matrix[N, D_rho] X_rho;
real lp_Y_cond;
real lp_beta_cond;
real lp_sigma2;
if (D_rho == 0) {
// rho_k が全て0の時だけ特別扱い
lp_Y_cond = normal_lpdf(Y | 0, sqrt(sigma2));
lp_beta_cond = 0;
lp_sigma2 = inv_gamma_lpdf(sigma2 | nu/2, s/2);
} else {
for (k in 1:D_rho){
b0_rho[k] = 0;
}
int beta_index = 1;
for (k in 1:D){
if(rho[k] == 1){
// 計画行列 X のうち rho_k=1 となる行・列から構成される主部分行列 X_rho を定義する
X_rho[,beta_index] = col(X, k);
beta_index += 1;
}
}
matrix[D_rho, D_rho] beta_cov_rho = generate_beta_cov_matrix(X_rho);
lp_Y_cond = normal_lpdf(Y | X_rho * beta_rho[1:D_rho], sqrt(sigma2));
lp_beta_cond = multi_normal_lpdf(beta_rho[1:D_rho] | b0_rho, sigma2 * beta_cov_rho);
lp_sigma2 = inv_gamma_lpdf(sigma2 | nu/2, s/2);
}
real lp_rho = 0;
for (i in 1:D) {
lp_rho += bernoulli_lpmf(rho[i] | rho_pi[i]);
}
return lp_Y_cond + lp_beta_cond + lp_sigma2 + lp_rho;
}
}
// The input data is a vector 'y' of length 'N'.
data {
int N;
int D;
matrix[N, D] X;
vector[N] Y;
// for out-of-sample prediction
int N_new;
matrix[N_new, D] X_new;
}
// The parameters accepted by the model.
parameters {
real<lower=0> sigma2;
vector<lower=0, upper=1>[D] rho_pi;
array[to_int(2^D)] vector[D] beta_rhos;
}
transformed parameters {
//vector[N] mu;
//
//mu = X*beta;
real tau = 1/sigma2;
}
// The model to be estimated. We model the output
// 'y' to be normally distributed with mean 'mu'
// and standard deviation 'sigma'.
model {
vector[to_int(2^D)] lp;
array[D] int rho;
for (i in 1:D) {
rho[i] = 0;
}
// parameters for sigma^2 prior
real nu = 0.01;
real r2 = 0.5;
real sy = variance(Y);
real s = nu * (1-r2) * sy;
// model definition
// rho=(0,0,...,0) ~ (1,1,...,1) までの全パターンで対数尤度を計算する
for (k in 1:to_int(2^D)) {
// Y|beta,sigma2,rho の対数尤度を定義
lp[k] = spike_and_slab_regression_lpdf(Y | X, beta_rhos[k], sigma2, nu, s, rho, rho_pi);
// ベクトル rho を更新
int rho_increment = 1;
for (i in 1:D) {
int tmp_added = rho[i] + rho_increment;
if (tmp_added==2) {
rho[i]=0;
} else {
rho[i] = tmp_added;
rho_increment = 0;
}
}
}
//print("log_sum_exp(lp): ", log_sum_exp(lp));
target += log_sum_exp(lp);
}
Stan による Spike-and-Slab 回帰の実装試行:補足
これまで Stan による Spike-and-Slab 回帰の実装を2通り試したが、いずれもうまくいかず、回帰係数の事後サンプリング値がとてつもなく大きな値になっていた。
その原因として考えていたものに、モデル記述の際に parameter として定義した回帰係数 beta から要素を取り出したり slice を行ったことで、参照渡しではなく値渡をしてしまっていたからではないか、というものがある。
しかし、これは違いそうだとわかった。
以前問題なく実行できた「緩やかな Spike-and-Slab 事前分布」を用いた回帰において、モデル記述の際に回帰係数 beta をわざと slice して入れてみた。
- lp[k] = normal_lpdf(Y | X * beta, sqrt(sigma2)) + multi_normal_lpdf(beta | beta0, sigma2 * inverse(beta_prec_mat)) + inv_gamma_lpdf(sigma2 | nu/2, s/2);
+ lp[k] = normal_lpdf(Y | X * beta[1:D], sqrt(sigma2)) + multi_normal_lpdf(beta[1:D] | beta0, sigma2 * inverse(beta_prec_mat)) + inv_gamma_lpdf(sigma2 | nu/2, s/2);
その結果、この場合でも問題なく実行でき、実行結果もこれまでと変わらなかった。
したがって、parameter で vector として定義した変数を slice してモデルを記述しても問題ないことがわかり、少なくとも 2つ目の実装 がうまくいかなかった原因は別にあるものと考えられる。
Gibbs Sampling による Spike-and-Slab 回帰
Stan は使わず、
ピーター・D・ホフ(入江 薫・菅澤 翔之助・橋本 真太郎 訳)、「標準 ベイズ統計学」(朝倉書店、2022)の9.3.2節に基づく。
事後分布によるサンプリング
library(ggplot2)
library(dplyr)
library(MASS)
library(matrixStats)
library(forcats)
library(tidyr)
library(ggdist)
対数尤度を計算するための関数
calc_sigma_inv <- function(X) {
n <- dim(X)[1]
xt_x <- t(X) %*% X
return(0.5 * (xt_x + diag(diag(xt_x), ncol=dim(xt_x)[1])) / n)
}
calc_omega_inv <- function(X) {
Sigma_inv <- calc_sigma_inv(X)
xt_x <- t(X) %*% X
return(xt_x + Sigma_inv)
}
calc_S_y_rho <- function(y, X, s) {
res <- s + t(y) %*% y
if(dim(X)[2]==0) {
return(res)
}
omega_inv <- calc_omega_inv(X)
tilde_beta <- solve(omega_inv) %*% t(X) %*% y
return(res - t(tilde_beta) %*% omega_inv %*% tilde_beta)
}
log_p_y_rho <- function(y, X, nu, s) {
# log P(Y | rho) から定数分を除いたもの
# log |Sigma_rho^{-1}| - log |Omega_rho^{-1}| - 0.5 * (n + nu) * log S_{Y,rho}
n <- dim(X)[1]; p <- dim(X)[2]
if(p==0) {
return(-0.5 * (n+nu) * log(s + t(y) %*% y))
}
det_sigma_inv_rho <- det(calc_sigma_inv(X))
det_omega_inv_rho <- det(calc_omega_inv(X))
S_y_rho <- calc_S_y_rho(y, X, s)
return(log(det_sigma_inv_rho) - log(det_omega_inv_rho) - 0.5 * (n + nu) * log(S_y_rho))
}
Gibbs Sampling of rho
y <- input_data$y
X <- matrix(x_des, ncol=6)
# 初期値とMCMCの設定
nu <- 0.01
r2 <- 0.5; sy <- variance(y)
s <- nu * (1 - r2) * sy
p <- dim(x_des)[2]
rho <- rep(1, p)
lpy_prev <- log_p_y_rho(y, X, nu, s)
n_iter <- 10000
Z <- matrix(NA, n_iter, p)
# Gibbs Sampler
for (i in 1:n_iter) {
for (k in sample(1:p)) {
rho_tmp <- rho; rho_tmp[k] <- 1 - rho_tmp[k]
lpy_new <- log_p_y_rho(y, X[,rho_tmp==1, drop=FALSE], nu, s)
log_odds <- (lpy_new - lpy_prev) * (-1)^(rho_tmp[k]==0)
pi_k <- 1/(1+exp(-log_odds))
rho[k] <- rbinom(1,1,pi_k)
if(rho[k] == rho_tmp[k]){lpy_prev <- lpy_new}
}
Z[i,]<- rho
}
beta_rho, sigma2 のサンプリング
X_sample <- matrix(x_des_sample, ncol = dim(x_des_sample)[2])
n_sample <- dim(X_sample)[1]
sigma2_sampled <- matrix(NA, n_iter)
beta_sampled <- matrix(NA, n_iter, p)
mu_sampled <- matrix(NA, n_iter, n_sample)
y_post_pred <- matrix(NA, n_iter, n_sample)
n <- dim(X)[1]
for (i in 1:n_iter){
rho <- Z[i,]
X_rho <- X[,rho==1, drop=FALSE]
# Sampling sigma2
S_y_rho <- calc_S_y_rho(y, X, s)
sigma2_sample <- 1/rgamma(1, shape=(n + nu)*0.5, S_y_rho * 0.5)
sigma2_sampled[i] <- sigma2_sample
# Sampling beta_rho
if(dim(X_rho)[2]>0) {
omega_inv_rho_inv <- solve(calc_omega_inv(X_rho))
mean_beta_rho <- omega_inv_rho_inv %*% t(X_rho) %*% y
beta_rho <- mvrnorm(1, mu=mean_beta_rho, Sigma=sigma2_sample * omega_inv_rho_inv)
beta_sampled[i, rho==1] <- beta_rho
}
# Sampling mu and Y_post
X_sample_rho <- X_sample[,rho==1,drop=FALSE]
if (dim(X_rho)[2]>0){
mu <- X_sample_rho %*% beta_rho
} else {
mu <- matrix(0, n_sample)
}
mu_sampled[i,] <- mu
y_post_pred[i,] <- mu + rnorm(1, 0, sqrt(sigma2_sample))
}
結果の可視化
説明変数選択率 rho
mean_rho_post <- colMeans(Z)
df_rho_post <- data.frame(
name=seq(1, length(mean_rho_post)),
value=mean_rho_post
)
ggplot(data=df_rho_post, aes(x=fct_rev(as.character(name)), y=value)) +
geom_bar(stat = "identity") +
geom_text(aes(label = value), stat = "identity", hjust=1,colour = "white")+
coord_flip()

回帰係数(beta)・誤差項分散(sigma2)事後分布
df_params_post <- data.frame(beta_sampled, sigma2=sigma2_sampled) %>%
rename(beta1=X1, beta2=X2, beta3=X3, beta4=X4, beta5=X5, beta6=X6)
ggplot(data=gather(df_params_post)) +
stat_halfeye(
aes(y=fct_rev(key), x=value, fill=stat(cut_cdf_qi(cdf, .width = c(0.05, 0.95)))),
.width = c(0.50, 0.95),
#point_interval = median_hdci,
show.legend = FALSE)+
scale_fill_manual(values=c("blue", "skyblue"))+
geom_point(data=data.frame(beta=true_beta, index=c(7,6,5,4,3,2)), aes(x=beta, y=index), color="red", shape=18, size=4)+
geom_point(x=1,y=1, color="red", shape=18, size=4)
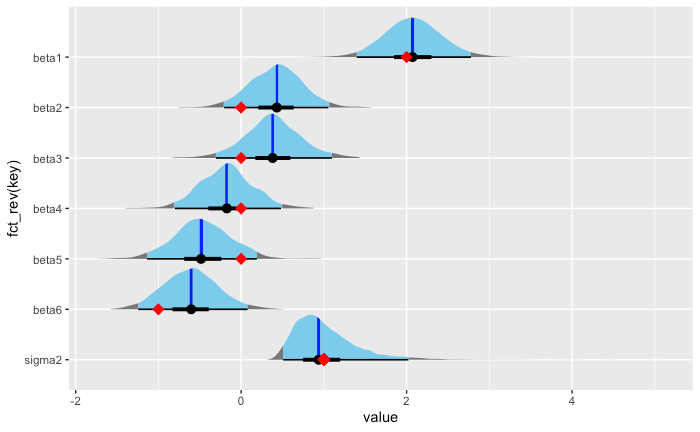
y 事後予測値
df_y_post_pred_sammary <- data.frame(x=x_sample, y_actual=y_sample, mean=colMeans(y_post_pred), colQuantiles(y_post_pred, prob=c(0.025,0.50,0.975))) %>%
rename(q2.5=`X2.5.`, q50=`X50.`, q97.5=`X97.5.`)
ggplot(data=df_y_post_pred_sammary) +
geom_point(data=input_data, aes(x=x, y=y), size=3)+
geom_line(aes(x=x, y=q50), color="blue") +
geom_line(aes(x=x, y=y_actual), linetype="dashed") +
geom_ribbon(aes(x=x, ymin=q2.5, ymax=q97.5), fill="blue", alpha=0.25)
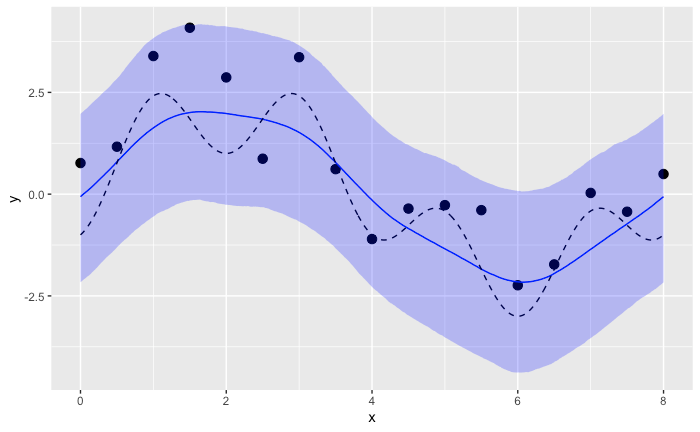
mu = X_rho * beta_rho 事後予測値
df_mu_sampled_sammary <- data.frame(x=x_sample, y_actual=y_sample, mean=colMeans(mu_sampled), colQuantiles(mu_sampled, prob=c(0.025,0.50,0.975))) %>%
rename(q2.5=`X2.5.`, q50=`X50.`, q97.5=`X97.5.`)
ggplot(data=df_mu_sampled_sammary) +
geom_point(data=input_data, aes(x=x, y=y), size=3)+
geom_line(aes(x=x, y=q50), color="blue") +
geom_line(aes(x=x, y=y_actual), linetype="dashed") +
geom_ribbon(aes(x=x, ymin=q2.5, ymax=q97.5), fill="blue", alpha=0.25)
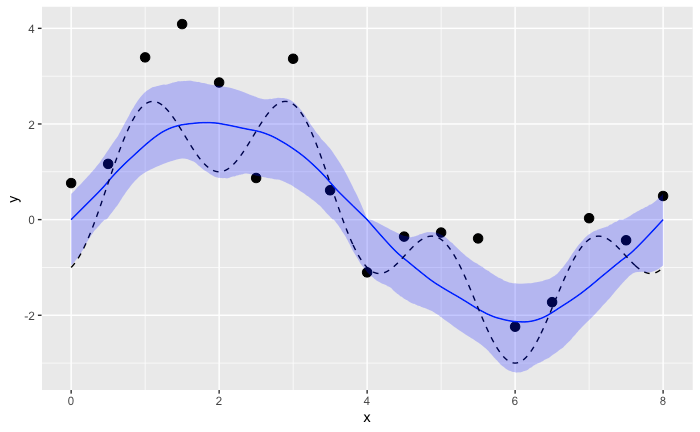
サンプル軌道
p<-ggplot(data=df_mu_sampled_sammary) +
geom_point(data=input_data, aes(x=x, y=y), size=3)+
geom_line(aes(x=x, y=y_actual), linetype="dashed")
for(i in seq(1,n_iter,by=50)) {
df_single_sample <- data.frame(x=x_sample, y=mu_sampled[i,])
p <- p + geom_line(data=df_single_sample, aes(x=x, y=y), color="blue", alpha=0.25)
}
print(p)

PyMC で CausalImpact と同様の Spike-and-Slab 事前分布を実装できるか?
CausalImpact の同様に
結果、うまくいかなかった。
モデル実装
以下のように選択変数 rho の和に応じて回帰モデルを書き分け、回帰係数 beta_rho(
# モデルの定義
## 事前分布およびそのハイパーパラメータは、下記の論文を参考にした
## Brodersen, Kay H., Fabian Gallusser, Jim Koehler, Nicolas Remy, and Steven L. Scott. "Inferring causal impact using Bayesian structural time-series models." (2015): 247-274.
## Scott, Steven L., and Hal R. Varian. "Predicting the present with Bayesian structural time series." International Journal of Mathematical Modelling and Numerical Optimisation 5, no. 1-2 (2014): 4-23.
def get_exact_ssreg_model(y, X):
n = y.shape[0]
p = X.shape[1]
model = pm.Model()
s_y2 = np.var(y, ddof=1)
nu = 0.01
R2 = 0.5
s = nu * (1 - R2) * s_y2
with model:
rho = pm.Bernoulli('rho', .5, shape=p)
tau = pm.Gamma('tau', nu/2, s/2)
sigma2 = 1/tau
p_rho = sum(rho)
if p_rho == 0:
mean = 0
else:
X_rho = X[:, rho==1]
Sigma_rho = 0.5 * np.matmul(X_rho.T, X_rho) / n
Sigma_rho += np.diag(np.diag(Sigma_rho))
beta_rho = pm.MvNormal('beta_rho', 0, tau=tau * Sigma_rho, shape=p_rho)
mean = pm.math.dot(X_rho, beta_rho)
y_obs = pm.Normal('y_obs', mean, tau=tau, observed=y)
return model
exact_ssreg_model = get_exact_ssreg_model(y, x_des)
with exact_ssreg_model:
# draw 1000 posterior samples
idata_exact_ssreg = pm.sample()
実行結果
---------------------------------------------------------------------------
ValueError Traceback (most recent call last)
<ipython-input-27-e3069b6e0140> in <cell line: 1>()
----> 1 exact_ssreg_model = get_exact_ssreg_model(y, x_des)
2
3 with exact_ssreg_model:
4 # draw 1000 posterior samples
5 idata_exact_ssreg = pm.sample()
<ipython-input-26-66a0aee61878> in get_exact_ssreg_model(y, X)
27 else:
28 X_rho = X[:, rho==1]
---> 29 Sigma_rho = 0.5 * np.matmul(X_rho.T, X_rho) / n
30 Sigma_rho += np.diag(np.diag(Sigma_rho))
31 beta_rho = pm.MvNormal('beta_rho', 0, tau=tau * Sigma_rho, shape=p_rho)
ValueError: matmul: Input operand 1 has a mismatch in its core dimension 0, with gufunc signature (n?,k),(k,m?)->(n?,m?) (size 0 is different from 17)
そもそも、rho = pm.Bernoulli('rho', .5, shape=6) で定義した rho を numpy.array のように扱うことに無理があった。
実際、以下を実行してみると分かるように rho は長さが6のベクトルにはならず、 X_rho には [] が入ることになる。
model = pm.Model()
with model:
rho = pm.Bernoulli('rho', .5, shape=6)
print(rho)
print(rho == 1)
print(x_des[:, rho==1])
>> rho
>> Add.0
>> False
>> []