論文
前回記事 で、いったん Transformer 系列の紹介は終わりにして、状態空間モデルに移ります。
最終的に Is Mamba Effective for Time Series Forecasting? を紹介したいのですが、理論背景が非常に複雑なので、今回は下記の論文まで遡ってご紹介します。
S4論文は数学的に難しく、その解説（といっても全ては理解しきれていないですが...）だけで手いっぱいなので、「理論編」と「実装編」で分けます。今回は「理論編」です。
タイトル
Efficiently Modeling Long Sequences with Structured State Spaces
論文: https://arxiv.org/pdf/2111.00396
Github: https://github.com/state-spaces/s4
S4理解のためのステップ
S4は、状態空間モデル(SSM)を実用的な計算量で学習する事を目的としています。
S4を理論的に理解するためのステップを描いてみました。かっちりとした区分では無く、あくまで雰囲気として捉えてください。もしかすると、上記以外にも実は背景として非常に重要だった要素が漏れているかもしれませんが、ご了承ください。
※コメントでご指摘いただけると幸いです。
S4に関連する前段階の論文として、以下の２つがあります。
これらを引き継ぐ形で本論文があります。以下の解説では、論文AでXを証明、論文BでYを証明、といった明確に役割を区別した解説をせず、あくまでS4理解のために体系的に数式などを解説する事とします。
①状態空間モデル
まずは、連続時間の状態空間モデル（SSM）を解説します。
\begin{aligned}
\frac{dx(t)}{dt}&=Ax(t)+Bu(t) & \\
y(t)&=Cx(t)+Du(t) & (1)
\end{aligned}
※論文では D=0 としているので、本記事でもその前提で解説します。
ここで u(t) は時刻tでの入力、x(t) は時刻tの内部状態、y(t) は時刻tの出力を表します。
と、言われてもこれはいったい何なんだ、となるかもしれません。実は、自然界の様々な事象はこの式で表現できるそうです。電磁気学におけるRC回路や、力学でのばね振り子の運動方程式などがそれに当たります。
と、言われても私にはまだ分からなかったのでさらに簡単な例をChatGPTに聞くと、以下の例を説明されました。
-
x(t): 預金額
-
A: 銀行の金利
-
u(t): 入金額（B=1）
-
\frac{dx(t)}{dt}: ある時刻tの預金額の変動
-
y(t): 何でも良いのですが、例えば「支出」（預金残高に応じて生活水準も高くなる的な）
といった感じで、何となく雰囲気が分かります。
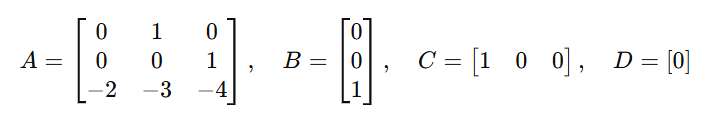
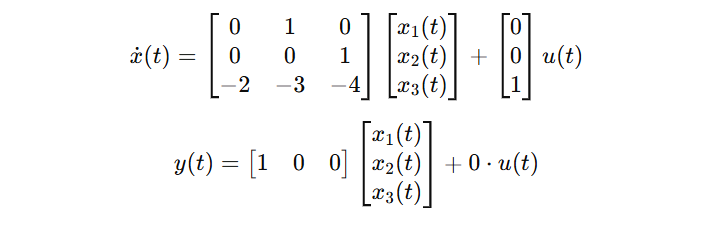
具体的な数値を当てはめてみるとこのような感じです。
u(t)がモデルへの入力、x(t)は内部状態、y(t)はモデルの出力、A,B,C(+\alpha) は学習するパラメータです。が、このパラメータを学習するための工夫が、どんどん式を難解にします。
逐次的な処理は遅い？
さて、ご存じの通り Transformer は 時系列に対してGPUで並列化する事 で大幅に計算時間を削減しています。RNNのような 1ステップずつ時系列を逐次的(Recurrent)に処理する仕組みでは並列化できず（時刻t+1の計算には時刻tの計算結果が必要なため）、計算に時間がかかるのです。
状態空間モデルの学習を、Transformer 同様 並列化 して学習を 高速化 する必要があります。そこで重要になるのが、後に出てくる 畳み込み(Convolution) です。
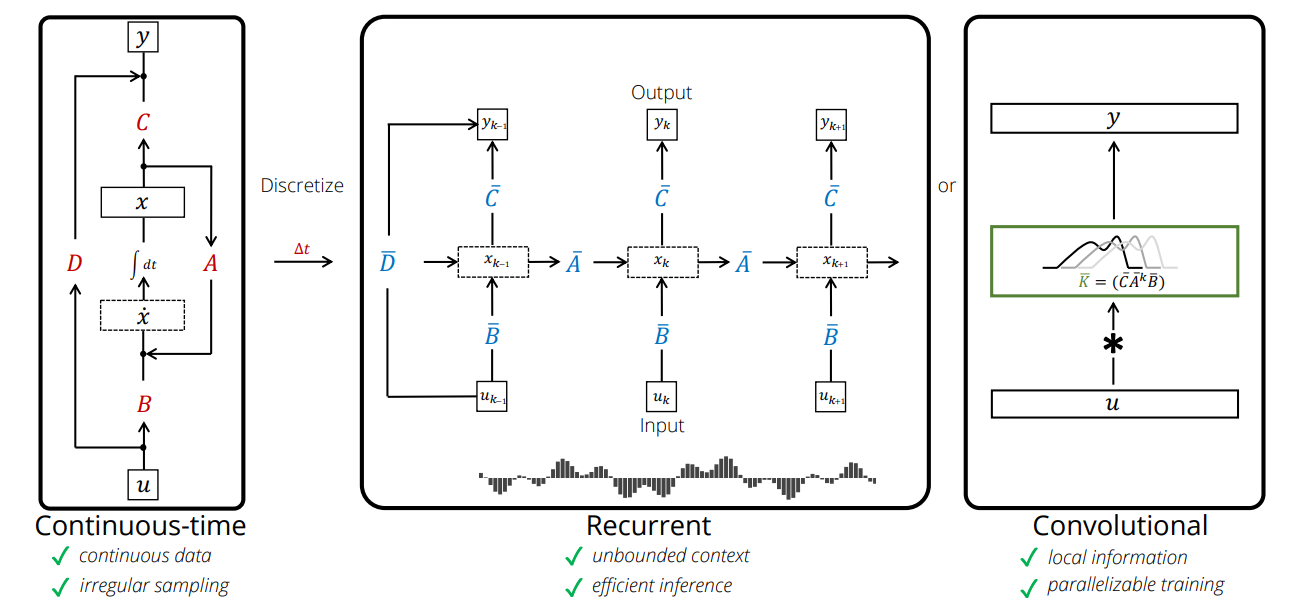
LSSLでも、学習は畳み込みで高速に学習し、推論は逐次的に行う仕組みとなっています。畳み込みに関しては後に解説します。
②状態空間モデルの離散化
さて、(1)は連続時間の定式化ですが、世の多くのデータは離散的にサンプリングされているため、離散化したバージョンの定式化を行います。
台形則
\int_{a}^{b}f(x)dx \thickapprox \frac{h}{2}(f(a)+f(b)), h=b-a
を適用すると
x_{k+1}-x_{k}=\int_{k}^{k+1}(Ax(t)+Bu(t))dt \thickapprox \frac{\Delta}{2}[Ax_k + Bu_k + Ax_{k+1} + Bu_{k+1}]
\left( I - \frac{\Delta}{2}A \right)x_{k+1}=\left( I + \frac{\Delta}{2}A \right)x_{k} + \frac{\Delta}{2}B \left( u_{k+1} + u_k \right)
入力 u_k を区間内で一定 u_k=u_{k+1} を仮定し、変形すると以下になります。
\left( \frac{2}{\Delta}I - A \right)x_{k+1}=\left( \frac{2}{\Delta}I + A \right)x_{k} + B \left( u_{k+1} + u_{k+1} \right)
s=\frac{2}{\Delta} とおくと
x_{k+1} = \left( sI - A \right)^{-1}\left( sI + A \right)x_k + \left( sI - A \right)^{-1}2 B u_{k+1}
論文に合わせて k \rightarrow k-1 として
\begin{aligned}
x_{k} &= \={A} x_{k-1} + \={B} u_k & \\
y_k &= \={C} x_{k} & (2)
\end{aligned}
ここで
\={A}=\left( sI - A \right)^{-1}\left( sI + A \right), \ \ \={B}=\left( sI - A \right)^{-1}2B, \ \ \={C}=C\ \ (3)
としました。
パラメータの学習が困難？
さて、これで定式化できたので、あとは A,B,C(or \={A},\={B},\={C}) というパラメータをデータから学習するだけ... となるはずですが、その学習は現実的に困難です。難しいとされる理由は以下に挙げられます。
- （後に出てくる）カーネルK の同値性
カーネルを計算するための A,B,C は相似変換によって無限に存在し、パラメータ空間に余計な自由度が多く、勾配が迷子になりやすい。
- 計算効率の壁
一般のA だとカーネルK(i)の計算が重く、不安定。
- 長期記憶に必要な「時間スケール分布」が当たりにくい
長時系列依存には、極小から極大まで広い時定数が必要。ランダム初期化だと短期寄りに偏りやすく、過去の入力へ向かう勾配が \| {\={A}}^i \| で指数減衰して届かない（つまり、過去の入力が忘却され意味をなしにくい）。
このままでは学習が難しいため、パラメータを工夫する必要が出てきます。その点を考えたのが、HiPPO となります。
③行列Ａの設計
パラメータの学習は難しく、それならば理論的な枠組みでパラメータの動作をある程度保障してやろう、という研究論文が HiPPO です。
この論文では以下の問題解決を図ろうと考えています。
- 連続的に流れてくるデータの「これまでの履歴」を、限られた状態量で失わずに保持しながらオンラインに更新したい
- 従来のRNNは「どれくらい昔まで覚えていられるか」が保証されない（勾配消失など）
- 多くの手法は「このくらいの長さの系列を想定」などのタイムスケール前提（ハイパラ）に強く依存してしまう。また、理論保証（勾配境界など）も弱い
そこで、SSMの行列Aに、理論的な枠組みで長期的に記憶可能なパラメータとして、この HiPPO-LegS が提案されました。
x_{k+1} = \left( I - \frac{A}{k} \right) x_k + \frac{1}{k}B u_k
A_{n,m}=
\begin{cases}
\sqrt{(2n+1)(2m+1)} & (n>m) \\
n+1 & (n=m) \\
0 & (n<m)
\end{cases}
, \ B_n=\sqrt{2n+1} \ \ \ (4)
これの何が良いのかというと、ある時系列点k+1 では全ての u_0 ～ u_k までが、1/k のスケールで x_{k+1} に組み込まれている、という事が理論的に保障されている点です。つまり、 どんなに時系列が長くても、同じスケールで全ての時点iを考慮 します。
スケールが等しい事の確認例
\tilde{x}_{k}^{(0)} を展開してみる。
\tilde{x}_{k}^{(0)} = \frac{k-1}{k}\tilde{x}_{k-1}^{(0)} + \frac{1}{k}u_{k} = \frac{k-1}{k}\left( \frac{k-2}{k-1}\tilde{x}_{k-2}^{(0)} + \frac{1}{k-1}u_{k-1} \right) + \frac{1}{k}u_{k}
=\frac{k-2}{k}\tilde{x}_{k-2}^{(0)}+\frac{1}{k}u_{k-1}+\frac{1}{k}u_{k}
\tilde{x}_{k}^{(0)} の箇所は、この後展開しても重みが全てのu_iが1/kでスケールしている事が分かる。
\tilde{x}_{k}^{(1)} を展開してみる。
\tilde{x}_{k}^{(1)} = \frac{k-2}{k}\tilde{x}_{k-1}^{(1)} - \frac{1}{k}\tilde{x}_{k-1}^{(0)} + \frac{1}{k}u_{k} = \frac{k-2}{k}\tilde{x}_{k-1}^{(1)} + \tilde{x}_{k}^{(0)} - \tilde{x}_{k-1}^{(0)}
となり、u_k の項が無くなった。\tilde{x}_{k}^{(0)} では u_i は 1/k でスケールしているため、\tilde{x}_{k}^{(1)} もまた、u_i は同じスケールを持つこととなる。
証明とはほど遠いが、何となくこの行列が、全ての過去情報を等しい重みで保持している事が分かると思う。
④SSMの畳み込み
さて、行列Aについての方針は得られたので、ここからは実際に計算するための定式化を行います。このSSMは、式変形すると「畳み込み」の形式に展開できます。
畳み込みができると何が便利？
畳み込み形式に展開できると、離散フーリエ変換（DFT）と逆離散フーリエ変換（IDFT）を使う事で、そのまま計算するよりも高速に計算する事が可能です。
参考にした記事を貼っておきます。
https://qiita.com/51_24_11_/items/11c48395603670ea98d8
離散化SSMの畳み込み
畳み込みの「カーネル」と呼ばれる項は（論文を一部流用しますが）、以下のようなカーネル \={K} になります。
\={K} = \left( \={C} \={B}, \={C} \={A} \={B}, ..., \={C} {\={A}}^{L-1} \={B} \right) = \left( k_0, k_1, ..., k_{L-1} \right)
\={K}はL次元のベクトルです。各CA^iBという各要素の値は、計算するとスカラーになります。
\={K} = K_Lと書き直すと以下です。
畳み込み計算は、DFTとIDFTを使って以下のように書けます。
DFT(y) = DFT(K_L \ast u) = DFT(K_L) \odot DFT(u) \ \ \ (6)
y = IDFT(DFT(K_L) \odot DFT(u)) \ \ \ (7)
記号の意味ついて、以下に ChatGPT 解説を貼っておきます。また、連続時間のSSM(1)の畳み込み形式への式展開についても記載しておきます。
畳み込みと要素積
連続時間のSSMの畳み込み式展開
突拍子もなく \frac{d}{dt}[e^{-At}x(t)] という計算を考えてみると
\frac{d}{dt}[e^{-At}x(t)]=-Ae^{-At}x(t) + e^{-At}\frac{dx(t)}{dt}=-Ae^{-At}x(t) + e^{-At}(Ax(t)+Bu(t))
両辺を (0 ~ t) 積分すると
e^{-At}x(t)-x(0)=\int_{0}^{t}e^{-A\tau}Bu(\tau)d\tau
x(t)=\int_{0}^{t}e^{A(t-\tau)}Bu(\tau)d\tau + e^{At}x(0)
となり、x(t) は u(\tau) の積分で求まります。さらに x(t) を使うと
y(t)=Ce^{At}x(0)+\int_{0}^{t}Ce^{A(t-\tau)}Bu(\tau)d\tau
=Ce^{At}x(0)+\int_{0}^{t}h(t-\tau)u(\tau)d\tau
となり、これはカーネル h(t)=Ce^{At}B の畳み込みとなります。そしてこちらは、y(t) が初期状態 x(0) と時系列の入力 u(0) ～ u(t) までを与えると、並列的に計算できる事が現れています。
さらなるカーネルの展開
このカーネル列の母関数（generating function）として {\hat{K}}_L を定義してみます。
{\hat{K}}_L(z; \={A},\={B},\={C})=\sum_{i=0}^{L-1} k_iz^i = \sum_{i=0}^{L-1} \={C} {\={A}}^i \={B} z^i \ \ \ (8)
ここでは、k_i は行列で、zはダミー変数でスカラーです（フーリエ変換ではz^iとなる多項式について考えます）。この {\hat{K}}_L は実は、DFT(K_L)={\hat{K}}_L となっています。
DFT(K)の詳細
畳み込みではカーネル関数のフーリエ変換を考えるので、つまりフーリエ変換後の{\hat{K}}_L（DFT(K_L)）をそのまま深堀します。
級数の和 1+x+x^2+...+x^{n-1}=(1+x^n)/(1-x) を応用すれば、以下のようにも表現できます。
\sum_{i=0}^{L-1} \left( \={A} z \right)^i = \left( I - (\={A}z)^L \right) \left( I - \={A}z \right)^{-1}
{\hat{K}}_L(z)= \={C} \left( \sum_{i=0}^{L-1} {\={A}}^i z^i \right) \={B} = \={C} \left( I - (\={A}z)^L \right) \left( I - \={A}z \right)^{-1} \={B}
ここで、
z=\omega_L^k \colonequals e^{-2\pi i k/L} \left( k=0,...,L-1 \right)
となるため、
{\hat{K}}_L(z)= {\hat{K}}_L(\omega_L^k) = \={C} \left( I - \={A}^L \right) \left( I - \={A} \omega_L^k \right)^{-1} \={B}
= \tilde{C} \left( I - \={A} \omega_L^k \right)^{-1} \={B} \ \ \ (9)
※\ \ \tilde{C}=\={C} \left( I - \={A}^L \right) \ \ \ (10)
\tilde{C}については、全てのkで共通の値で、計算量は多くありません。
しかし、\left( I - \={A} \omega_L^k \right)^{-1} は各kについて別々に 逆行列を求める必要があり計算が大変 です。
以下の解説では、この逆行列をどう効率的に計算するかの説明になります。
⑤HiPPO-LegS → NPLR → DPLR
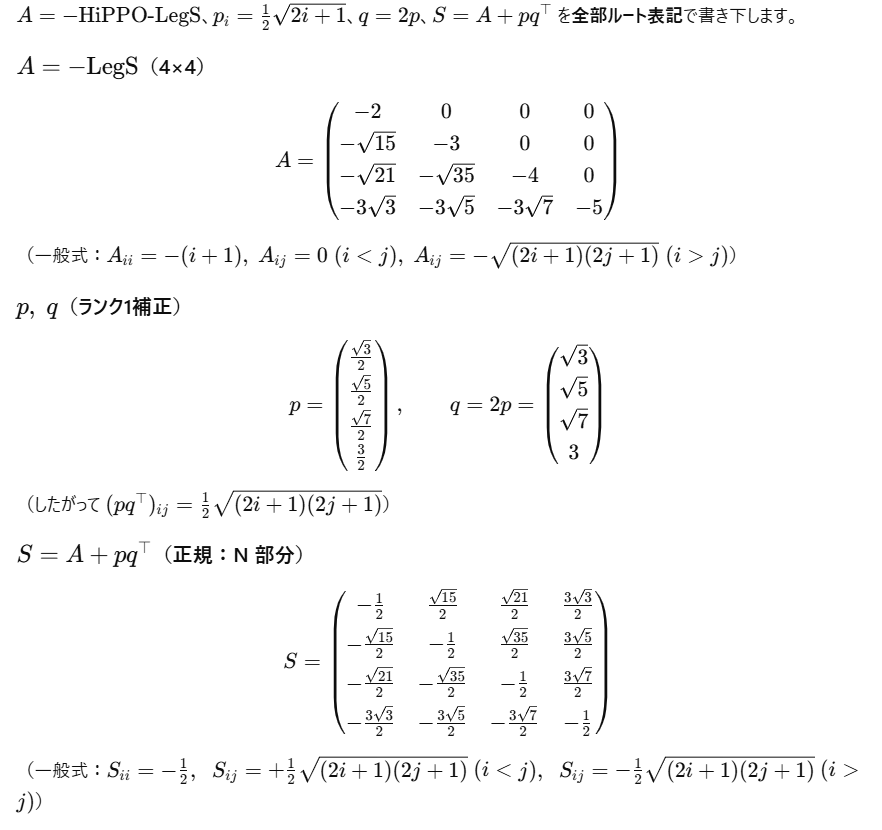
さて、③行列Aの設計で HiPPO-LegS という行列A_{LegS} を得ました。
NPRL
この行列は NPLR ( Normal Plus Low-Rank ) という性質を持ちます。Sは正規行列です。
A_{LegS}=S-pq^T \ \ \ (11)
この p, q は N x r 行列（通常r=1）で、それが Low Rank の所以です。
NPLRへの式変形の計算例の紹介
DPLR
正規行列SをユニタリVで固有分解S=V\Lambda V^* すれば論文の式(6)を得ます。
A_{LegS}=V\Lambda V^* - pq^T=V\left( \Lambda - (V^* p)(V^* q)^* \right) V^* \ \ \ (12)
式展開の詳細
V\left( \Lambda - (V^* P)(V^* Q)^* \right) V^*=V\Lambda V^* - V(V^* P)(V^* Q)^* V^*
(V^* Q)^* V^*=Q^*VV^*=Q^* I=Q^*=Q^T
※共役転置なので、実数においては転置と同じである
よって、
V\left( \Lambda - (V^* p)(V^* q)^* \right) V^*=V\Lambda V^* - pq^T=S-pq^T=A
(12)の式で P=V^*p, Q=V^*q とおき、VとV^*を両方からかけると
V^*AV=\Lambda - PQ^* = A' \ \ \ (13)
を得ます。このA'は DPLR ( Diagonal Plus Low-Ran ) となります。このように、固有値＋Low-Rank な行列で書ければ後の式展開で有利のため、このA'が使えるように、(2)式を変形していきます。
SSMをA'が使えるように変形
(2)式を次のように変形します。
\begin{aligned}
x_{k}&=\={A}x_{k-1}+\={B}u_k \\
&=\={A}VV^*x_{k-1}+V^*\={B}u_k \\
V^*x_{k}&=V^*\={A}VV^*x_{k-1}+V^*\={B}u_k \\
y_{k}&=\={C}VV^*x_k
\end{aligned}
\={A}'=V^*\={A}V,\ \ \={B}'=V^*\={B},\ \ \={C}'=\={C}V,\ \ h_k=V^*x_k \ \ \ (14)
とおくと
\begin{aligned}
h_{k}&=\={A}'h_{k-1}+\={B}'u_k & \\
y_{k}&=\={C}'h_k & \ \ \ (15)
\end{aligned}
これは、内部状態xをV^*だけ回転させただけで、実はもとの空間状態モデルと同一です。そしてこの\={A}'は、以下のようにA'が含まれる形式となります。
\={A}'=V^*\={A}V=\left( sI-A' \right)^{-1}\left( sI+A' \right) \ \ \ (16)
A'への式展開の詳細
V^*\={A}V=V^* \left( sI-A \right)^{-1}\left( sI+A \right)V
=V^* \left( sI-A \right)^{-1} VV^* \left( sI+A \right)V
さて、ここで右半分は以下のように展開できる。
V^* \left( sI+A \right)V = sI+V^*AV=sI+A'
左半分は、「逆行列の相似変換」の基本恒等式 S^{-1}M^{-1}S=(S^{-1}MS)^{-1} と V^{-1}=V^* というユニタリ行列の性質を使います。
V^* \left( sI-A \right)^{-1} V=\left( V^* \left( sI-A \right) V \right)^{-1}=\left( sI-A' \right)^{-1}
となり、結局のところ式(16)になります。
さて、畳み込みカーネル{\hat{K}_L} \rightarrow {\hat{K}_L}'は同様に展開できるので、
\begin{aligned}
{\hat{K}_L}'(z; \={A}',\={B}',\={C}')&=\={C}'(I-{\={A}'}^L)(I-\={A}'z)^{-1}\={B}' & \\
&=\tilde{C}'(I-\={A}'z)^{-1}\={B}' & (17)
\end{aligned}
となります。当たり前ですが、同様に逆行列が出てきます。この計算を効率化するのに、A'が使えると便利なのです。それを次の章から解説します。
⑥z因子化 + Woodbury
この章は数学のテクニックによる式展開の解説なので、重要じゃないと思う方は軽く読み飛ばしてください。
式(17)の (I-\={A}'z)^{-1}\={B}' について考えます。
z因子化
さて、\={A}'の係数となっている z が、このままでは使いにくいので、zを\={A}'から剥がします。式は以下のように展開できます。
(I-\={A}'z)^{-1}\={B}'=\frac{2}{1+z} \left( \frac{1-z}{1+z}sI - A' \right)^{-1}B' \ \ \ (18)
ここで、B'=V^* B と置きました。
z因子化の詳細
\={B}'は式(3),(14)から
\begin{aligned}
(I-\={A}'z)^{-1}\={B}'&=(I-\={A}'z)^{-1}V^*(sI-A)^{-1}2B \\
&=(I-\={A}'z)^{-1} \left( V^*(sI-A)^{-1}V \right) V^* 2B \\
&=(I-\={A}'z)^{-1} (sI-A')^{-1} 2B' \\
\end{aligned}
ここで、B'=V^*B と置いた。X^{-1}Y^{-1}=(YX)^{-1} の変換を使えば
(I-\={A}'z)^{-1}\={B}'=\left((sI-A')(I-\={A}'z)\right)^{-1}2B'
となる。また(16)より、 \={A}'=(sI-A')^{-1}(sI+A') なのでそれを代入すると
\begin{aligned}
(sI-A')(I-\={A}'z) &= sI-A' -(sI - A')\={A}'z \\
& =sI-A' -(sI+A')z \\
& =sI-zsI-A' -zA' \\
& =(1-z)sI-(1+z)A' \\
& =(1+z)\left( \frac{1-z}{1+z}sI - A' \right)
\end{aligned}
\deltaを戻して、元の式に入れると
\begin{aligned}
(I-\={A}'z)^{-1}\={B}' & =\left( (1+z)\left( \frac{1-z}{1+z}sI - A' \right) \right)^{-1}2B' \\
& =\frac{2}{1+z}\left( \frac{1-z}{1+z}sI - A' \right)^{-1}B'
\end{aligned}
さて、もう少し簡単に計算できるように変形します。
Woodbury を使った変形
Woodburyの行列恒等式は以下のように表せます。
(M+UV^*)^{-1}=M^{-1}-M^{-1}U(I+V^*M^{-1}U)^{-1}V^* M^{-1}
ここでR(z)を以下のように定義します。R(z)は 対角行列 になっています（\Lambda が対角行列で、括弧の中身も対角行列になり、その逆行列も対角行列になるので）。
R(z)=\left( \frac{1-z}{1+z}sI-\Lambda \right)^{-1}
R(z)とWoodburyの変換を使うと、式(18)の逆行列の箇所は、以下のように変形できます。
\begin{aligned}
\left( \frac{1-z}{1+z}sI - A' \right)^{-1} & = \left( \frac{1-z}{1+z}sI - \Lambda + PQ^* \right)^{-1} \\
& = \left( {R(z)}^{-1} + PQ^* \right)^{-1} \\
& =R(z)-R(z)P(I+Q^*R(z)P)^{-1}Q^*R(z) \ \ \ (19)
\end{aligned}
一見複雑になっただけのようですが、いったいこれの何がうれしいのかというと、(...)^{-1} の計算が楽になる事 です。
式の左辺では A'の状態で、これは PQ^* が含まれ N x N 行列です。この逆行列の計算は大変です。
しかし、式変形を行うと右辺の様になり、計算が非常に簡単になります。項の一部を見てみると
-
Q^*R(z)P: r x r行列
-
I+Q^*R(z)P: r x r行列
S4ではr=1であり、(I+Q^*R(z)P)^{-1}の項は実質スカラーになり、計算が楽です。これが、この複雑な式変形の嬉しい効果です。
⑦ カーネルK計算
さて、これで逆行列を効率的に計算する準備が整い、つまりカーネルのフーリエ変換{\hat{K}_L}'(z)が計算できるようになりました。式(17)を(18),(19)を使って書き表すと
\begin{aligned}
{\hat{K}_L}'(z) & =\tilde{C}'(I-\={A}'z)^{-1}\={B}' \\
& =\tilde{C}'\frac{2}{1+z}\left( R(z)-R(z)P(I+Q^*R(z)P)^{-1}Q^*R(z) \right) B' \\
& =\frac{2}{1+z} \left( \tilde{C}'R(z)B' - \tilde{C}'R(z)P(I+Q^*R(z)P)^{-1}Q^*R(z)B' \right)
\end{aligned} \ \ \ (20)
となります。そしてこの項をよく見ると、次の４つを計算する必要があります。
- \tilde{C}'R(z)B'
- \tilde{C}'R(z)P
- Q^*R(z)B'
- Q^*R(z)P
これらは行列Kの様に書く事ができて
K=\begin{bmatrix}
\tilde{C}' \\
Q^*
\end{bmatrix} R(z)
\begin{bmatrix}
B' & P
\end{bmatrix} =
\begin{bmatrix}
\tilde{C}'R(z)B' & \tilde{C}'R(z)P \\
Q^*R(z)B' & Q^*R(z)P
\end{bmatrix} =
\begin{bmatrix}
k_{00} & k_{01} \\
k_{10} & k_{11}
\end{bmatrix} \ \ \ (21)
(20)
{\hat{K}_L}'(z)=\frac{2}{1+z}\left( k_{00}(z) - k_{01}(z)(1+k_{11}(z))^{-1}k_{10}(z) \right) \ \ \ (22)
となり、これを計算する事で{\hat{K}_L}'(z)を計算できます。
⑧ yの計算
さて、ここまでくれば後は少しです。式(7)と同じ事を行います。
今、DFT(K)={\hat{K}_L}'は得られましたので、あとは以下を計算すれば y が求まります。
y=IDFT({\hat{K}_L}' \odot DFT(u))
最後に
ある程度、自分自身で納得のいくまで深堀して理解できたのではないかと思います。とはいえ、ところどころ厳密ではない式展開もまだあるかと思いますが、比較的満足のいく記事にできたと思います。
間違い等ありましたら、コメントでご指摘いただけるとありがたいです。
実装なくして、真に理解したとは言えないでしょう。次の実装編では、具体的にどう計算しているのか、を解説できればと思います。
参考
https://recruit.gmo.jp/engineer/jisedai/blog/is-attention-all-you-need/
https://techblog.morphoinc.com/entry/2022/05/24/102648
https://srush.github.io/annotated-s4/
https://zenn.dev/izmyon/articles/c56a2fd6670546#ssmカーネルの計算に伴う課題
Discussion