🐔
その他言語モデル論文解説③「RWKV v7」

2025/11/03に公開
 論文RWKV-7 "Goose" with Expressive Dynamic State Evolution
論文: https://arxiv.org/pdf/2503.14456

GitHub: https://github.com/BlinkDL/RWKV-LM

wiki: https://wiki.rwkv.com/basic/architecture.html
現時点(2025/10/31)では最新version です。

 前提知識
 RWKV v4, v5, v6変更点を記述するスタイルで解説しますので、前バージョンの解説は前提とします。

RWKV v4, v5, v6

 取り扱う次元
C: \bold{x}_t の特徴量次元. n_embd

D(=C): \bold{W}_{\square} によって射影される次元（だったもの）. dim_att. 実装においては、全てCに置き換わっている

h: ヘッド数. ヘッド次元は D/h

 lerp少しだけ表記が変わっているので、改めます。

\text{lerp}(\bold{a}, \bold{b}, \pmb{\mu}) = \bold{a} + (\bold{b} - \bold{a}) \odot \pmb{\mu}

 loramlp
\text{loramlp}_{\square}(f, \bold{x}, \pmb{\lambda}_{\square}=\bold{0}) = f(\bold{x} \bold{A}_{\square})\bold{B}_{\square} + \pmb{\lambda}_{\square}(\text{or}\ \ \bold{0})
書き方が厳密ではありませんが、\pmb{\lambda}_{\square}=\bold{0} のように bias なしとしても機能するという意味です。また、以前の lora との関係性は以下になります。

\text{lora}_{\square}(.) = \text{loramlp}_{\square}(\text{tanh}, \bold{x}, \pmb{\lambda}_{\square})

 v6 から変わっていない箇所基本的に全て変わっています。モデル全体のブロック構造自体は変わっていないです。

 v6 から変わった箇所
Token Shift で ddlerp をやめて元の lerp に戻した

\bold{u} が無くなり、 \bold{w}_t に統合された形
パラメータも色々と増え、WKV term がより複雑になった（後述）
WKV Bonus という項が増えた

 Time Mixing ( Token Shift )まず、以下のようにシンプルな lerp に戻しています。添え字がややこしくなっているので注意してください。
https://github.com/BlinkDL/RWKV-LM/blob/b3b4d056d0907bb9e9619be3de077f051091287c/RWKV-v7/train_temp/src/model.py#L166-L173

\begin{align*}
\bold{x}_t^{r} &= \text{lerp}(\bold{x}_t, \bold{x}_{t-1}, \pmb{\mu}_r) \ \ \ \in \mathbb{R}^{C} \\
\bold{x}_t^{d} &= \text{lerp}(\bold{x}_t, \bold{x}_{t-1}, \pmb{\mu}_d) \ \ \ \in \mathbb{R}^{C} \\
\bold{x}_t^{k} &= \text{lerp}(\bold{x}_t, \bold{x}_{t-1}, \pmb{\mu}_k) \ \ \ \in \mathbb{R}^{C} \\
\bold{x}_t^{v} &= \text{lerp}(\bold{x}_t, \bold{x}_{t-1}, \pmb{\mu}_v) \ \ \ \in \mathbb{R}^{C} \\
\bold{x}_t^{a} &= \text{lerp}(\bold{x}_t, \bold{x}_{t-1}, \pmb{\mu}_a) \ \ \ \in \mathbb{R}^{C} \\
\bold{x}_t^{g} &= \text{lerp}(\bold{x}_t, \bold{x}_{t-1}, \pmb{\mu}_g) \ \ \ \in \mathbb{R}^{C} \\
\end{align*}
\bold{W}_{\square} による射影です。また、\bold{v}_t は今回から layer の場所lによって値の持ち方が変わってます。\bold{v}_{t,l}' と表記します。
https://github.com/BlinkDL/RWKV-LM/blob/b3b4d056d0907bb9e9619be3de077f051091287c/RWKV-v7/train_temp/src/model.py#L175
https://github.com/BlinkDL/RWKV-LM/blob/b3b4d056d0907bb9e9619be3de077f051091287c/RWKV-v7/train_temp/src/model.py#L177-L178

\begin{align*}
\bold{r}_t &= \bold{x}_t^{r} \bold{W}_r \ \ \ \in \mathbb{R}^{C} \\
\bold{k}_t &= \bold{x}_t^{k} \bold{W}_k \ \ \ \in \mathbb{R}^{C} \\
\bold{v}_{t,l}' &= \bold{x}_t^{v} \bold{W}_v \ \ \ \in \mathbb{R}^{C} \\
\end{align*}
以下の v_first first layer で得られた \bold{v}_{t,0}' を後ろの layer でも使うために変数に移しています。そして、layer $ > 0$ の箇所では、初期 layer で得られた \bold{v}_{t,0}' との差分を \pmb{\nu}_t の割合で更新しています（何故これを行っているかは分かりません...）。
https://github.com/BlinkDL/RWKV-LM/blob/b3b4d056d0907bb9e9619be3de077f051091287c/RWKV-v7/train_temp/src/model.py#L179-L182

\begin{align*}
\pmb{\nu}_t &= \text{sigmoid}(\text{loramlp}_v ( \text{Identity}, \bold{x}_t^v, \pmb{\lambda}_v) \ \ \ \in \mathbb{R}^{C} \\
\bold{v}_{t} &= \text{lerp}(\bold{v}_{t,0}', \bold{v}_{t,l}', \pmb{\nu}_t) \ \ \ \in \mathbb{R}^{C} \\
\end{align*}
今回から \bold{k}_t を直接使うのではなく、さらに加工した \bold{\tilde{k}}_t という値を使います。また 0 < \bold{a}_t < 1 です。
https://github.com/BlinkDL/RWKV-LM/blob/b3b4d056d0907bb9e9619be3de077f051091287c/RWKV-v7/train_temp/src/model.py#L183
https://github.com/BlinkDL/RWKV-LM/blob/b3b4d056d0907bb9e9619be3de077f051091287c/RWKV-v7/train_temp/src/model.py#L186-L188

\begin{align*}
\bold{a}_t &= \text{sigmoid} \left( \text{loramlp}_a ( \text{Identity}, \bold{x}_t^a, \pmb{\lambda}_a) \right) \ \ \ \in \mathbb{R}^{C} \\
\pmb{\kappa}_t &= \bold{k}_t \odot \pmb{\xi} \ \ \ \in \mathbb{R}^{C} \\
\pmb{\hat{\kappa}}_t &= \frac{\pmb{\kappa}_t}{\Vert \pmb{\kappa}_t \Vert} \ \ \ \in \mathbb{R}^{C} \\
\bold{\tilde{k}}_t &= \bold{k}_t \odot \text{lerp}(1, \bold{a}_t, \pmb{\alpha}) \ \ \ \in \mathbb{R}^{C}　\\
\end{align*}
結局 \bold{\tilde{k}}_t というのが分かりにくいですが、式を展開してみると以下になります。-1 < \bold{a}_t - 1 < 0 で \pmb{\alpha} は単なるパラメータなので、正負をとります。こう見ると、\bold{\tilde{k}}_t の値を少し割合増減して調整している感じでしょうか？　うーん...。

\bold{\tilde{k}}_t = \bold{k}_t + (\bold{a}_t - 1) \odot \pmb{\alpha} \odot \bold{k}_t

 Time Mixing ( WKV kernel (term) )今バージョンから kernel という呼び方に代わっていますね。さて、まずは \bold{w}_t を求めます。
https://github.com/BlinkDL/RWKV-LM/blob/b3b4d056d0907bb9e9619be3de077f051091287c/RWKV-v7/train_temp/src/model.py#L176
https://github.com/BlinkDL/RWKV-LM/blob/b3b4d056d0907bb9e9619be3de077f051091287c/RWKV-v7/train_temp/cuda/wkv7_cuda.cu#L21

\begin{align*}
\bold{d}_t &= \text{loramlp}_d (\text{tanh}, \bold{x}_t^{d}, \pmb{\lambda}_{d}) \ \ \ \in \mathbb{R}^{C} \\
\bold{d}_t' &= -\text{softplus}(-\bold{d}_t) - 0.5 \ \ \ \in \mathbb{R}^{C} \\
\bold{w}_t &= \exp ( - e^{\bold{d}_t'} ) = \exp ( - e^{-0.5} \sdot e^{-\text{softplus}(-\bold{d}_t)} )\\
\end{align*}
-\infin < -\text{softplus}(-\bold{d}_t) < 0 のため 0 < e^{-\text{softplus}(-\bold{d}_t)} < 1 となり \text{sigmoid}(\bold{d}_t) の形式を満たします。
次はいよいよ WKV の計算です。(h)はヘッド位置を表します。※hは本来ヘッド数を表しますが、分かりやすさのため(h)をそのまま使います。
https://github.com/BlinkDL/RWKV-LM/blob/b3b4d056d0907bb9e9619be3de077f051091287c/RWKV-v7/train_temp/src/model.py#L190

\bold{wkv}_t^{(h)} = \sum_{i=1}^{t} \left( {\bold{v}_{i}^{(h)}}^T \bold{\tilde{k}}_i^{(h)} \prod_{j=i+1}^t \left( \text{diag}(\bold{w}_j^{(h)}) - {\pmb{\hat{\kappa}}_j^{(h)}}^T (\bold{a}_j^{(h)} \odot \pmb{\hat{\kappa}}_j^{(h)}) \right)  \right) \ \ \ \in \mathbb{R}^{(C/h) \times (C/h)}
v6 との大きな違いは以下でしょう。

\bold{u} が無くなり、 \bold{w}_t に統合された形

\bold{k}_t が \bold{\tilde{k}}_t になった

\text{diag}(\bold{w}_t) の項が \text{diag}(\bold{w}_t) - {\pmb{\hat{\kappa}}_t}^T (\bold{a}_t \odot \pmb{\hat{\kappa}}_t) になった
v6 との比較v6 の形式は以下です。なるべく似るように変形してみます。

\text{wkv}_t^{(h)} = \text{diag}(\bold{u}^{(h)}) {\bold{k}_t^{(h)}}^T \bold{v}_t^{(h)} + \sum_{i=1}^{t-1} \text{diag} \left( \bigodot_{j=i+1}^{t-1}\bold{w}_j^{(h)} \right) {\bold{k}_i^{(h)}}^T \bold{v}_i^{(h)} \in \mathbb{R}^{(D/h) \times (D/h)}
まずは、\bold{u} が消えて、\bold{w}_t に統合されているような形です。また、\bigodot も \prod に変わっています。それを踏まえて、v6 の数式を少し変形します。

\bold{wkv}_t^{(h)} = \sum_{i=1}^{t} \prod_{j=i+1}^{t} \left( \text{diag} ( \bold{w}_j^{(h)} ) \right) {\bold{k}_i^{(h)}}^T \bold{v}_i^{(h)} \in \mathbb{R}^{(C/h) \times (C/h)}
\bold{k}と\bold{v} の順番も逆になっていますが、\text{diag}(\bold{w}) との行列積の順番も逆になっているので、その変化は打ち消し合っている感じです。
各パラメータの意味については後の章で解説を試みます。この RUN_CUDA_RWKV7g の出力は以下までを含んでいます。

\bold{p}_t' = \text{concat}_h ( \bold{r}_t^{(h)} \sdot {\bold{wkv}_t^{(h)}}^T ) \ \ \ \in \mathbb{R}^C

 Time Mixing ( WKV Bonus )新しく bonus という概念が増えています。例の如く、なぜこんな式になっているのかは分かりません...。Time Mixing の出力までを計算します。
https://github.com/BlinkDL/RWKV-LM/blob/b3b4d056d0907bb9e9619be3de077f051091287c/RWKV-v7/train_temp/src/model.py#L155
https://github.com/BlinkDL/RWKV-LM/blob/b3b4d056d0907bb9e9619be3de077f051091287c/RWKV-v7/train_temp/src/model.py#L184
https://github.com/BlinkDL/RWKV-LM/blob/b3b4d056d0907bb9e9619be3de077f051091287c/RWKV-v7/train_temp/src/model.py#L191-L194
nn.GroupNormについて実装では nn.GroupNorm(H, C, eps=64e-5) となっている。これは C の特徴量次元を H ヘッド数でグループ分けして、そのグループ単位で LayerNorm をする操作である。
つまり、ヘッド次元毎に LayerNorm している。
>>> x = torch.rand(2, 4)
>>> x
tensor([[0.2215, 0.7966, 0.4608, 0.8135],
        [0.1800, 0.4919, 0.2666, 0.8556]])
>>> f = torch.nn.GroupNorm(1,4, eps=64e-5)
>>> f(x)
tensor([[-1.4163,  0.9001, -0.4522,  0.9684],
        [-1.0233,  0.1652, -0.6935,  1.5516]],
       grad_fn=<NativeGroupNormBackward0>)
>>> f = torch.nn.GroupNorm(2,4, eps=64e-5)
>>> f(x)
tensor([[-0.9962,  0.9962, -0.9899,  0.9899],
        [-0.9871,  0.9871, -0.9963,  0.9963]],
       grad_fn=<NativeGroupNormBackward0>)
>>> f = torch.nn.GroupNorm(4,4, eps=64e-5)
>>> f(x)
tensor([[ 2.3352e-07, -4.1384e-07,  6.7491e-07, -2.4281e-07],
        [ 4.2385e-09, -2.8879e-07, -8.9960e-09, -7.5241e-07]],
       grad_fn=<NativeGroupNormBackward0>)

\begin{align*}
\bold{g}_t &= \text{loramlp}_g ( \text{sigmoid}, \bold{x}_t^g, \bold{0}) \ \ \ \in \mathbb{R}^{C} \\
\bold{p}_t'' &= \text{concat}_h \left( \text{LayerNorm}( {\bold{p}_t'}^{(h)} ) \right) \ \ \ \in \mathbb{R}^{C} \\
{u_t'}^{(h)} &= \sum_{ヘッド次元} \left( \pmb{\rho}^{(h)} \odot \bold{r}_t^{(h)} \odot \bold{\tilde{k}}_t^{(h)} \right) \ \ \ \in \mathbb{R} \\
\bold{u}_t^{(h)} &= {u_t'}^{(h)} \bold{v}_t^{(h)} \ \ \ \in \mathbb{R}^{C/h} \\
\bold{u}_t &= \text{concat}_h \left( \bold{u}_t^{(1)}, ..., \bold{u}_t^{(h)}, ... \right) \ \ \ \in \mathbb{R}^{C} \\
\bold{p}_t &= \bold{p}_t'' + \bold{u}_t \ \ \ \in \mathbb{R}^{C} \\
\bold{o}_t &= ( \bold{g}_t \odot \bold{p}_t ) \bold{W}_o \ \ \ \in \mathbb{R}^{C} \\
\end{align*}
LayerNorm の箇所が、CUDA側で concat した値に対し GroupNorm で処理しているので少し分かりづらいですが、式にすると上のようになります。

 Time Mixing ( RNN 形式 )

\begin{align*}
\bold{wkv}_0^{(h)} &= \bold{0} \\
\bold{wkv}_t^{(h)} &= \bold{wkv}_{t-1}^{(h)} \left( \text{diag}(\bold{w}_t^{(h)}) - {\pmb{\hat{\kappa}}_t^{(h)}}^T (\bold{a}_t^{(h)} \odot \pmb{\hat{\kappa}}_t^{(h)})  \right) + {\bold{v}_t^{(h)}}^T \sdot \bold{\tilde{k}}_t^{(h)}
\end{align*}

 MLP ( 旧 Channel Mixing )さらにシンプルになっており、Gating のための \bold{r}_t' が削除されています。
https://github.com/BlinkDL/RWKV-LM/blob/b3b4d056d0907bb9e9619be3de077f051091287c/RWKV-v7/train_temp/src/model.py#L220-L226

\begin{align*}
\bold{k}_t' &= \text{lerp}( \bold{x}_t, \bold{x}_{t-1}, \pmb{\mu}_{k'}) \bold{W}_{k'} \ \ \ \in \mathbb{R}^{4D} \\
\bold{o}_t' &= \text{ReLU}(\bold{k}_t')^2 \bold{W}_{v'} \ \ \ \in \mathbb{R}^D
\end{align*}

 モデルの背景順番が前後している感はありますが、このモデルに登場する数式の背景について説明します。

 線形アテンションの欠点線形アテンションでは固定サイズの状態に対して毎時刻数値的に加算を行うため、古い状態の内容は決して取り除かれず、数値的に増加し続ける状態に占める割合が小さくなることでしか減らない、という欠点があります。状態サイズに制限があるため、最終的にはそのような系は値を混ぜ合わせることになり、与えられたキーに対して取り出される出力が濁ってしまいます。
近年の線形アテンション系アーキテクチャ（RWKV-6 や Mamba-2）は、データ依存で時刻ごとの減衰（ RWKVの \bold{w}_t や Mamba の \Delta ）を用いてきましたが、減衰は粗い道具であり、特定のキーに保存された値だけを取り除くことはできません。

 Delta Rule※以下は、数式の気持ち的な話なので、厳密ではありません
線形アテンションにおける内部状態\bold{S} は \bold{S}=\sum_{i=1}^t \bold{v}_i^T \bold{k}_i のように書けます。この時、\bold{k}_i が規格化されているとして、\bold{S} \bold{k}_t^T という操作では \bold{v}_t^T の出力を期待したいです。
先行研究となる DeltaNet では、その差を損失関数として定義しています。

L_t=\frac{1}{2} \Vert \bold{S} \bold{k}_t^T - \bold{v}_t^T \Vert^2
そしてこれを \bold{S} で偏微分すると

\frac{\partial L_t}{\partial \bold{S}} = (\bold{S} \bold{k}_t^T - \bold{v}_t^T) \bold{k}_t
となり、これが内部状態S の更新式として導かれます。ここでの a は学習率のような係数です。

\bold{S}_t = \bold{S}_{t-1} (\bold{I} - a \bold{k}_t^T \bold{k}_t) + a \bold{v}_t^T \bold{k}_t 

 WKV kernel との比較さて、改めて今回の WKV の更新式を見てみます。少し書き換えた形式で示すと

\bold{wkv}_t = \bold{wkv}_{t-1} \left( \text{diag}(\bold{w}_t) - \left( \pmb{\hat{\kappa}}_t^T \pmb{\hat{\kappa}}_t \right) \sdot \text{diag}(\bold{a}_t)  \right) + \left( \bold{v}_t^T \bold{k}_t \right) \sdot \text{diag}(\text{lerp}(1, \bold{a}_t, \pmb{\alpha}))
\pmb{\hat{\kappa}}_t は規格化された \bold{k}_t と似た値なので、これは先ほどの更新式と類似します。※lerp の箇所が、何故シンプルな \bold{a}_t になっていないのかはよく分かりませんが...
この更新式のパラメータでは、以下のような意味を持ち得ます。

\pmb{\hat{\kappa}}_t: 内部状態から消す成分を特定する Key

\bold{k}_t: 内部状態に加える成分を決める Key

\bold{a}_t: in context な学習率
という感じで、一見複雑な数式も、背景となる理論によって構築されています。

 結果と所感
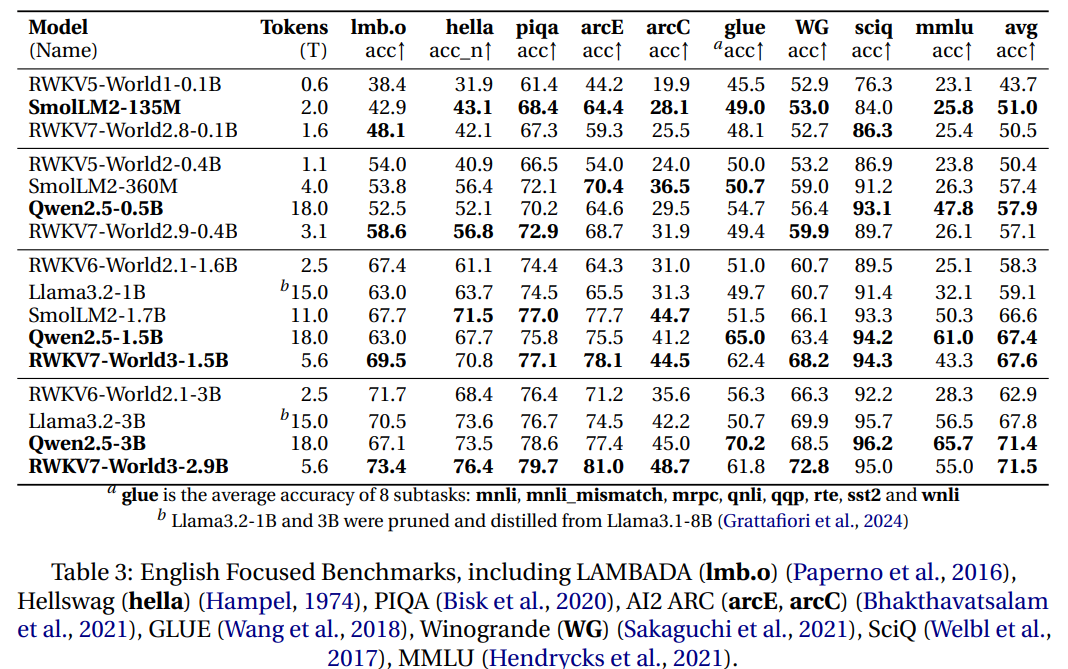
Multilingual では他を圧倒し、English focused では v6 と比べると他のモデルに肉薄するほど性能が追い付いています。
いずれにしても結果を考察するのは難しいですね。他のモデルや評価タスクについても詳しく無いので、込み入った内容は書けません。ただ何となく思うのは、Multiligual でこれほど良い性能を残しているのは、RNNの利点みたいなものが現れているから、かなと漠然と思っています。
RWKV v8 や Mamba-3 の GitHub が整備され出したら、また改めて解説記事を書きたいと思います。

 参考文献https://sustcsonglin.github.io/blog/2024/deltanet-1/