🐥
その他言語モデル論文解説①「RWKV v4」

2025/10/30に公開
 本記事の動機「時系列データの学習」という文脈において、有名な言語モデルの理解は避けて通れません。本ブログでもいくつかの言語モデルと、その応用について紹介してきました。この RWKV というシリーズも、注目すべき言語モデルであり、取り上げたいと思います。
もともとは、軽い言語モデルを探していて、その中でRNN派生のモデルがあるという事にたどり着きました。このRWKVもRNN派生モデルですし、以前ご紹介したMambaも、その仲間です。
また、最近になって「論文解説」を多数投稿していますが、数年前に比べてそういった記事はずいぶん減った印象があります。やはり ChatGPT 等があるので、今はわざわざ記事にしないのですかね。もしくは、言語モデル自体が巨大化しすぎて、個人の利用者に限って言えば、どう使えれば良いかが重要であり、その仕組みの理解は相対的に重要ではなくなってきたのかもしれません。
そういった想いもあって、そして自分自身の理解のために、こういった解説記事を投稿しています。

 論文RWKV: Reinventing RNNs for the Transformer Era
論文: https://arxiv.org/pdf/2305.13048

GitHub: https://github.com/BlinkDL/RWKV-LM

wiki: https://wiki.rwkv.com/basic/architecture.html
RWKV-V4 is the first official version of the RWKV architecture
となっているように、v4以降が official version のため、本記事も v4 をスタートとして解説します。

 概要Receptance Weighted Key Value（ RWKV ） を提案する
Transformerの効率的で並列化可能な学習と、RNNの効率的な推論を組み合わせた新しいモデルアーキテクチャである
線形アテンション機構を活用している（ヘッドの概念は無い）
Transformer 系モデルと同等のパフォーマンスを達成
全体的に論文の数式の次元が分かりにくかったため、ベクトルは全て \vec{x} 等で書いています。

 前提知識
 AFT ( Attention Free Transformer )RWKV では、このAFTから着想を経て、Attention like な計算構造を取り入れています。
https://developers.agirobots.com/jp/attention-free-transformer/
参考になる記事を貼っておきます。解説の中の人が以下の感想を残しており、私も同感です...
図にしてみたものの、なぜこのような計算式が思いつくのか、という疑問が私には残っていますが、内積計算を無くした代わりに少し複雑な仕組みを導入したんだろうな、という解釈で留めております...
数式を再掲します。\bold{q}_t, \bold{k}_t, \bold{v}_t \in \mathbb{R}^d, \bold{w} \in \mathbb{R}^{T \times T}

AFT(\bold{X}_t)=\sigma(\bold{q}_t) \odot \frac{\sum_{i=1}^{T} \exp (w_{t,i} + \bold{k}_i) \odot \bold{v}_i}{\sum_{i=1}^{T} \exp (w_{t,i} + \bold{k}_i)} \ \ \ \in \mathbb{R}^d
この式は、時刻t におけるAFTの出力を表してます。\bold{w} の箇所が少し分かりずらいので、分母の箇所だけ図示（T=4, d=3 の場合で、t=2の時の出力です）すると、以下になります。

 モデル構造さて、早速ですがモデル構造を見ていきましょう。実装と論文の絵や式を比較しながら解説したいと思います。
以下のソースコードをベースに解説します。
https://github.com/BlinkDL/RWKV-LM/blob/9f557219c42d48ec32d948220b427da0362634ad/RWKV-v4/src/model.py

 RWKV block全体構造及び RWKV block は以下のようになっています。
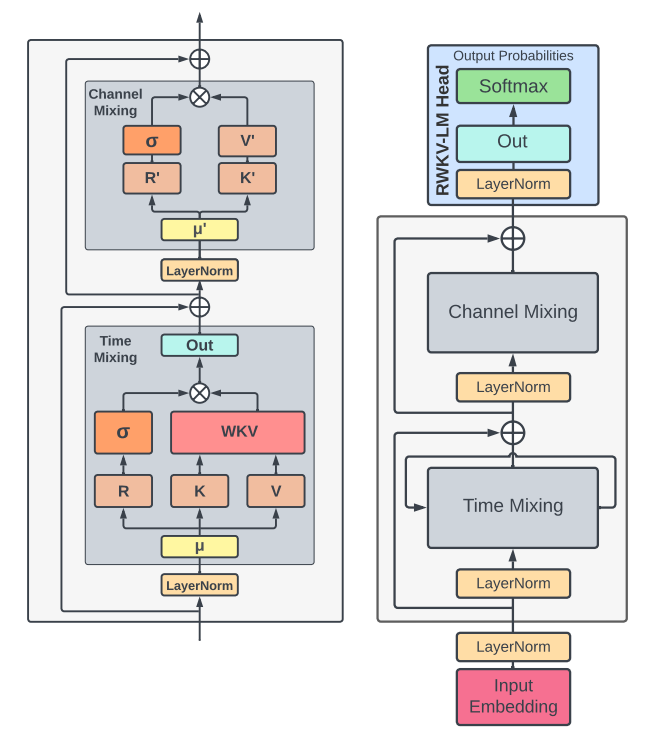
https://github.com/BlinkDL/RWKV-LM/blob/9f557219c42d48ec32d948220b427da0362634ad/RWKV-v4/src/model.py#L286
LayerNorm や残渣結合は Transformer と同じですね。Time Mixing と Channel Mixing が特徴的です。これは Time Mixing -> Attention ( WKT で重みづけ ), Channel Mixing -> FFN ( + ゲーティング機構 )と対応関係にあります。

 RWKV における RNN構造
先に、RWKVにおける RNN の構造を説明しておきます。
Token ShiftTime Mixing と Channel Mixing の両構造には、以下のようにひとつ前の 入力\vec{x} (※内部状態ではありません※) を一定の割合で混ぜるという構造が現れます。\vec{\mu} \in \mathbb{R}^{d}

\vec{x}_t' = \vec{\mu} \odot \vec{x}_t + (1 - \vec{\mu}) \odot \vec{x}_{t-1} \ \ \ \in \mathbb{R}^{d}
これが Token Shift です。
Statesこれは Time Mixing だけに見られる構造です。こちらは AFT を取り入れた構造と関係しますので、後述します。

 Time Mixingコードベースに解説します。
>>> from types import SimpleNamespace
>>> config = SimpleNamespace(n_embd=32, n_layer=4, ctx_len=16)
>>> self = RWKV_TimeMix(config, 1)
>>> self = RWKV_TimeMix(config, 1)
>>> self
RWKV_TimeMix(
  (time_shift): RecursiveScriptModule(original_name=ZeroPad2d)
  (key): RecursiveScriptModule(original_name=Linear)
  (value): RecursiveScriptModule(original_name=Linear)
  (receptance): RecursiveScriptModule(original_name=Linear)
  (output): RecursiveScriptModule(original_name=Linear)
)
まず、time_shift で入力をずらします。
https://github.com/BlinkDL/RWKV-LM/blob/9f557219c42d48ec32d948220b427da0362634ad/RWKV-v4/src/model.py#L212
>>> x = torch.rand(1, self.ctx_len, self.n_embd) # B, T, C=d (特徴量次元)
>>> x[:, :2]
tensor([[[0.4099, 0.4731, 0.2792, 0.1662, 0.2130, 0.0595, 0.5931, 0.6925,
          0.2968, 0.6595, 0.3455, 0.5869, 0.7043, 0.1886, 0.3415, 0.2438,
          0.0552, 0.2760, 0.5501, 0.5002, 0.0521, 0.3752, 0.7902, 0.0998,
          0.5462, 0.7990, 0.8720, 0.6791, 0.8916, 0.3277, 0.1551, 0.6417],
         [0.6335, 0.2077, 0.1743, 0.6647, 0.3094, 0.4457, 0.6124, 0.1912,
          0.7311, 0.6154, 0.7550, 0.8406, 0.3732, 0.5622, 0.1135, 0.6701,
          0.2051, 0.8791, 0.5207, 0.4800, 0.8069, 0.1481, 0.2847, 0.3455,
          0.9988, 0.1476, 0.1638, 0.2613, 0.8617, 0.3949, 0.5765, 0.1962]]])
>>> self.time_shift(x)[:, :2]
tensor([[[0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000,
          0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000,
          0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000,
          0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000],
         [0.4099, 0.4731, 0.2792, 0.1662, 0.2130, 0.0595, 0.5931, 0.6925,
          0.2968, 0.6595, 0.3455, 0.5869, 0.7043, 0.1886, 0.3415, 0.2438,
          0.0552, 0.2760, 0.5501, 0.5002, 0.0521, 0.3752, 0.7902, 0.0998,
          0.5462, 0.7990, 0.8720, 0.6791, 0.8916, 0.3277, 0.1551, 0.6417]]])
次に、x_{t-1} の情報を一定割合で混ぜます。
https://github.com/BlinkDL/RWKV-LM/blob/9f557219c42d48ec32d948220b427da0362634ad/RWKV-v4/src/model.py#L213-L215
ちなみに、各 \mu は次のような初期値を持っており、要素単位での混合になる旨注意してください。
>>> self.time_mix_k
Parameter containing:
tensor([[[0.0000, 0.0743, 0.1250, 0.1694, 0.2102, 0.2485, 0.2849, 0.3199,
          0.3536, 0.3862, 0.4180, 0.4489, 0.4792, 0.5089, 0.5379, 0.5665,
          0.5946, 0.6223, 0.6495, 0.6764, 0.7029, 0.7291, 0.7550, 0.7806,
          0.8059, 0.8310, 0.8558, 0.8804, 0.9047, 0.9288, 0.9527, 0.9765]]],
       requires_grad=True)
>>> self.time_mix_v
Parameter containing:
tensor([[[0.1000, 0.1743, 0.2250, 0.2694, 0.3102, 0.3485, 0.3849, 0.4199,
          0.4536, 0.4862, 0.5180, 0.5489, 0.5792, 0.6089, 0.6379, 0.6665,
          0.6946, 0.7223, 0.7495, 0.7764, 0.8029, 0.8291, 0.8550, 0.8806,
          0.9059, 0.9310, 0.9558, 0.9804, 1.0047, 1.0288, 1.0527, 1.0765]]],
       requires_grad=True)
>>> self.time_mix_r
Parameter containing:
tensor([[[0.0000, 0.2726, 0.3536, 0.4116, 0.4585, 0.4985, 0.5338, 0.5656,
          0.5946, 0.6215, 0.6465, 0.6700, 0.6922, 0.7133, 0.7334, 0.7527,
          0.7711, 0.7888, 0.8059, 0.8224, 0.8384, 0.8539, 0.8689, 0.8835,
          0.8977, 0.9116, 0.9251, 0.9383, 0.9512, 0.9638, 0.9761, 0.9882]]],
       requires_grad=True)
特徴量次元Cの、後ろの方の情報ほど重要視するように設定しており、なぜ特徴量次元でそういった decay をしているのか、正直謎です...。
次に WKV Operator ( AFT に代わるもの )への入力のため、k, v などを求めます。
https://github.com/BlinkDL/RWKV-LM/blob/9f557219c42d48ec32d948220b427da0362634ad/RWKV-v4/src/model.py#L218-L221
こちらは単純に k = Linear(xk) をしているだけです。
WKV Operator次に wkv を求めます。こちらは CUDA で実装されており、コードでは分かりにくいので、数式で解説します。また、スカラーなのかベクトルなのかが分かりにくかったため表記を変えています。
https://github.com/BlinkDL/RWKV-LM/blob/9f557219c42d48ec32d948220b427da0362634ad/RWKV-v4/src/model.py#L230
t, i \in \mathbb{R}, \vec{w}, \vec{u}, \vec{k}_t, \vec{v}_t  \in \mathbb{R}^{d}

\vec{wkv}_t = \frac{\sum_{i=1}^{t-1} \exp (-(t - 1 - i)\vec{w} + \vec{k}_i) \odot \vec{v}_i + \exp (\vec{u} + \vec{k}_t) \odot \vec{v}_t}{\sum_{i=1}^{t-1} \exp (-(t - 1 - i)\vec{w} + \vec{k}_i) + \exp (\vec{u} + \vec{k}_t)}
この計算がCUDAによって実装されています。そしてこれこそが、Time Mixing の所以です。まず、この \vec{w} と \vec{u} ですが、パラメータとなっており、以下のような値です。
>>> self.time_decay # w
Parameter containing:
tensor([-5.0000, -4.8367, -4.6419, -4.4330, -4.2144, -3.9883, -3.7561, -3.5186,
        -3.2766, -3.0305, -2.7807, -2.5276, -2.2713, -2.0122, -1.7504, -1.4861,
        -1.2195, -0.9506, -0.6796, -0.4066, -0.1317,  0.1451,  0.4237,  0.7039,
         0.9858,  1.2692,  1.5542,  1.8406,  2.1284,  2.4176,  2.7082,  3.0000],
       requires_grad=True)
>>> self.time_first # u
Parameter containing:
tensor([-1.2040, -0.7040, -1.7040, -1.2040, -0.7040, -1.7040, -1.2040, -0.7040,
        -1.7040, -1.2040, -0.7040, -1.7040, -1.2040, -0.7040, -1.7040, -1.2040,
        -0.7040, -1.7040, -1.2040, -0.7040, -1.7040, -1.2040, -0.7040, -1.7040,
        -1.2040, -0.7040, -1.7040, -1.2040, -0.7040, -1.7040, -1.2040, -0.7040],
       requires_grad=True)
\vec{u} は時刻 t のみにかかる係数、\vec{w}は 時刻 t=1 ～ t-1 までにかかる係数です。さらに \vec{w} は時間が過去のものほど減衰するようになっています。 \exp (-(t - 1 - i)\vec{w} + \vec{k}_i)=e^{-(t - 1 - i)\vec{w}} e^{\vec{k}_i} です。係数の変化を見てみましょう

\begin{align*}
i=1, & \ \ \ e^{-(t-2)\vec{w}} \\
i=2, & \ \ \ e^{-(t-3)\vec{w}} \\
\vdots & \\
i=t-2, & \ \ \ e^{-\vec{w}} \\
i=t-1, & \ \ \ e^{0} \\
\end{align*}
となります。（ただ、この w はパラメータとして正に制限している訳でもないので、発散とかしないのかな、と少し気になります。）
そして最後に出力を求めます。これらの一連の流れは (17)式です。
https://github.com/BlinkDL/RWKV-LM/blob/9f557219c42d48ec32d948220b427da0362634ad/RWKV-v4/src/model.py#L231
WKV Operator の内部状態( states )RNNの箇所で states に触れましたが、そちらについて解説します。wkv の計算は、次のような漸化式に変形できます。

\vec{a}_0=\vec{0}, \vec{b}_0=\vec{0}, \in \mathbb{R}^{d}

\vec{wkv}_t = \frac{\vec{a}_{t-1} + e^{\vec{u}+\vec{k}_t} \odot \vec{v}_t}{\vec{b}_{t-1} + e^{\vec{u} + \vec{k}_t}}

\begin{align*}
\vec{a}_t &= e^{-\vec{w}} \odot \vec{a}_{t-1} + e^{\vec{k}_t} \odot \vec{v}_t \\
\vec{b}_t &= e^{-\vec{w}} \odot \vec{b}_{t-1} + e^{\vec{k}_t} \\
\end{align*}
となり、こちらの \vec{a}, \vec{b} が内部状態として表現されています。

 Channel Mixinghttps://github.com/BlinkDL/RWKV-LM/blob/9f557219c42d48ec32d948220b427da0362634ad/RWKV-v4/src/model.py#L235
https://github.com/BlinkDL/RWKV-LM/blob/9f557219c42d48ec32d948220b427da0362634ad/RWKV-v4/src/model.py#L261-L271
コードで見ると計算は難しくないのですが、正直なぜこういう計算を行っているのかは分かりません。

 結果
この BLOOM, Pythia, OPT といったモデルは、Transformer ベースのモデルです。結果は、比較的同等の性能を示していると言えます。

 考察と所感もっと論文を読み込めば、パラメータや数式について、なぜそういう形になっているかの説明があるかもしれませんが、ぱっと見ではその数式の「気持ち」は分かりにくいものが多かったです。とりあえず後継モデルについても解説を試みます。以上