本記事はスタンフォード大学の田久保勇志(https://www.linkedin.com/in/yuji-takubo/ )による寄稿です。
はじめに
先日 Part 1 ということで、Covariance Steering の基本的な議論(線形ダイナミクスの行列化→凸最適化への持ち込みまで)を執筆しました。本記事は続編ということで、引き続き不確定性を 制御していきましょう!
今回の扱いたい項目は、大きく分けて二つあります。
- 確率的な最適化に対して(特にGaussian は上端下端がないunbounded な分布なので)、制約条件も確率的に取り扱いたいというのが自然な流れです。これを一般にChance Constraintと言ったりしますが、Covariance Steeringにおける状態および制御入力に対する確率的な制約の扱い方を導出し、凸性が保存されることを確認します。
- Covariance Steeringはフィードバックの制御入力を、経路設計の時点で生成できるという点で非常に魅力的ですが、それであれば現実世界の実装ではMPCとして扱いたい、という気持ちが出てきます。なので、MPCとしてCovariance Steeringを使っていくにはどのようにしたら良いか、ということに関しての議論を進めます。いわゆるStochastic MPCにおいては、(特に確率分布がunbounded, そして観測状態がアップデートされる度に)逐次的に実行可能解を出せる保証が弱く、どのようにそれを掻いくぐるかということがポイントです。
なるべく定性的な議論で押せるところは定性的に行きますが、数式が増えるので、前回記事のNomenclatureを参考にしながら読んでいただければ幸いです。
前回のおさらい
軽く前回のおさらいをします。(離散時間における) Covariance Steering では、始端・終端条件がGaussian で表現された、以下の最適制御問題を考えます。
\min \ \mathcal{J} = \mathbb{E} \left[ \sum_{k=0}^{N-1} x_k^T Q_k x_k + u_k^T R_k u_k \right] \\
x_{k+1} = A_k x_k + B_k u_k + D_k w_k, \quad k = 0, 1, ..., N \tag{2}\\
x_0 \sim \mathcal N (\mu_0, \Sigma_0), \quad x_f \sim \mathcal N (\mu_f, \Sigma_f)
この問題を、以下のように表現することができます(前回記事では、平均の制御(mean steering) と分散の制御 (covariance steering)を分けて書きましたが、制約が複雑になるにつれて分解できなくなるので、今回はまとめて表現します) 。
\begin{aligned}
\min \ & \mathcal{J}(V, K) = (\mathcal{A}\mu_0 + \mathcal{B} V)^T Q (\mathcal{A}\mu_0 + \mathcal{B} V) + V^TRV + \text{tr}[ (\mathbb{I}+\mathcal{B}K)^T Q ( ((\mathbb{I}+\mathcal{B}K) + K^T R K)\Sigma_Y ] \\
\text{s.t.} \ &
\begin{bmatrix}
\Sigma_N & Z \\
Z^T & \mathbb{I}
\end{bmatrix} \succeq 0, \quad Z := E_N(\mathbb{I}+\mathcal{B}K) \Sigma_Y ^{\frac{1}{2}} \\
\text{where} \ & \bar{X} = \mathcal{A}\mu_0 + \mathcal{B} V \quad (\text{平均のダイナミクス}) \\
& U = KY + V = K (\mathcal{A}y_0 + \mathcal{D}W) + V, \quad y_0 = x_0 - \mu_0 \\
& \Sigma_Y = \mathcal{A} \Sigma_0 \mathcal{A}^T + \mathcal{D}\mathcal{D}^T \succ 0 \\
& E_k \bar{X} = \mu_k, \forall k = 0, ..., N \\
& E_k \Sigma_Y E_k^T = \Sigma_k, \forall k = 0,...,N \\
& F_k U = u_k = K_k y_k + v_k, \forall k = 0, ..., N-1\\
& X = \begin{bmatrix} x_0^T, x_1^T, ... , x_N^T\end{bmatrix}^T, \\
& U = \begin{bmatrix} u_0^T, u_1^T, ... , u_N^T\end{bmatrix}^T, \\
& W = \begin{bmatrix} w_0^T, w_1^T, ... , w_N^T\end{bmatrix}^T
\end{aligned}
スペースの都合で行列\mathcal{A}, \mathcal{B}, \mathcal{D}の導出は省略しますが、状態履歴ベクトルXが制御/ノイズの履歴を縦につなげたベクトルU,Wおよび初期値のx_0, \mu_0, \Sigma_0によって表現できるようにするためにダイナミクスを圧縮して表現しています。E_k, F_kはX,U から k-step目の変数を呼ぶ行列です。制御Uは、平均からのズレの蓄積Yに対してのフィードバック項KYと、平均を動かすための制御Vの和になっています。
確率的制約条件の取り扱い
(制御に限らず)不確定性のある最適化に対して、どのように制約をかけていくかというのは非常に重要な問題です。例えばもし確率分布が閉じているなら取りうる最悪のケースを確定的な制約に置き換える、離散的な確率分布ならパターンをすべて書き出す等、色々ありますが、今回はXX%の確率で制約を満たすというようなChance Constraint を考えます。
これは一般に、以下のように記述できます。
\tag{1}
\begin{align}
& \text{Pr}(x \in \mathcal{X}) \geq 1 - \Delta_x \\
& \text{Pr}(x \in \mathcal{U}) \geq 1 - \Delta_u
\end{align}
前回の記事 の変数をもって表すと、
\tag{2}
\begin{align}
& \text{Pr}(E_kX \in \mathcal{X}) \geq 1 - \Delta_x, \forall k \\
& \text{Pr}(F_kU \in \mathcal{U}) \geq 1 - \Delta_u, \forall k
\end{align}
ここでE_k, F_kは状態変数/制御変数を縦に積んだベクトルから、k番目の要素を抽出している (x_k, u_k) ことを示しています。
ここで、\text{Pr}(\cdot) は確率を表し、\Delta_x, \Delta_u \in [0,1] は制約が満たされない確率を示すパラメータと定義されます。
これが実行可能解領域が線形制約の集合である場合、次のようにあらわされます。
\tag{3}
\mathcal{X} = \bigcap_{i = 0 }^{N_s -1 } \lbrace x : \alpha_{x.i}^T x \leq \beta_{x,i}\rbrace , \quad
\mathcal{U} = \bigcap_{i = 0 }^{N_c -1 } \lbrace u : \alpha_{u.i}^T u \leq \beta_{u,i}\rbrace ,
ここでN_s とN_c は状態変数(state) と制御(control) の制約の数を定義します。今回は簡単のため、この線形制約が時間に依らず一定であるとします。(時間で制約が変化する場合でも、同様の処理ができます)
さて、この制約を直接評価するのは難しい(N_s個の個々の制約が満足されているかの確率/累積分布関数(CDF)で、その制約で作られるpolytope の中に状態が存在する確率を直接表現することは難しい)ので、ブールの不等式 (有限加算の事象の集合に対して、その和集合の中の事象が(i.e., どれか事象が一つ以上)起こる確率は、一つ一つの事象の確率の和よりも小さい)を用いて、たとえば状態変数の制約群は、各タイムステップkにおいて、以下のような保守的な制約条件に書き換えることができます。(Eq. (4)はEq. (3)の十分条件です。)
\tag{4}
\text{Pr}(\alpha_{x.i}^TE_kX \leq \beta_{x,i}) \geq 1 - p_{x,i}, \quad \sum_{j=1}^{N_s} p_{x,i} \leq \Delta_x, \quad \forall k
これによって、一つ一つの制約に対してリスク分配を行い、制約評価を可能にしています。ここではシンプルに、p_{x,i} = \Delta_x / N_s を採用します。
ここで、変数x\in \mathbb{R}^nの分布がGaussian の場合、Gaussian のCDF \Phi(\cdot)を以て次のような式が成り立つことで知られています。
\tag{5}
\text{Pr}(a^Tx\leq b) = \Phi\left(\frac{b- a^Tx}{\sqrt{x^T\Sigma x}}\right)
Eq. (4) の個々の制約はスカラーなので、Gaussian のCDFを用いて、以下のように表現することができます。\Phi^{-1}(\cdot)の値は、数値的に求めることが可能です(e.g., MATLAB: \texttt{norminv}関数)。
\tag{6}
\text{Pr}(\alpha_{x.i}^TE_kX \leq \beta_{x,i}) \geq 1 - p_{x,i} \Leftrightarrow \left(\frac{\beta_{x,i}-\alpha_{x.i}^TE_k\bar{X}}{\sqrt{\alpha_{x.i}^T\Sigma_X\alpha_{x.i}}}\right) \geq \Phi^{-1}(1-p_{x,i})
\tag{7}
\Leftrightarrow \left(\frac{\beta_{x,i}-\alpha_{x.i}^TE_k\bar{X}}{\sqrt{\alpha_{x.i}^TE_k(I + \mathcal{B}K)\Sigma_Y(I + \mathcal{B}K)^TE_k^T\alpha_{x.i}}}\right) \geq \Phi^{-1}(1-p_{x,i})
\tag{8}
\Leftrightarrow {\alpha_{x.i}^TE_k\bar{X}}+{||S^T(I + \mathcal{B}K)^TE_k^T\alpha_{x.i}}|| \Phi^{-1}(1-p_{x,i}) \leq \beta_{x,i}
と、変数\bar{X} = \mathbb{E}[X](制御の平均値Vから導出されます)とKに対して、錐形の制約に持ち込むことができました。直感的には、通常の線形制約 {\alpha_{x.i}^TE_kX} \leq \beta_{x,i}に対して、\Phi^{-1}(1-p_{x,i})を含むロバスト項を足すことで、制約を確率分布に対して拡張できるようにしている、という理解ができればOKです!
これと同様の導出を制御 U = KY + V に対しても行うことができ、これは以下のように表現されます。
\tag{8}
\text{Pr}(\alpha_{u.i}^TF_kU \leq \beta_{u,i}) \geq 1 - p_{u,i} \Leftrightarrow {\alpha_{u.i}^TF_kV}+{||S^TK^TF_k^V\alpha_{u.i}}|| \Phi^{-1}(1-p_{u,i}) \leq \beta_{u,i}
以上の拘束を用いて、Covariance steeringにおける線形制約の処理が可能になりました。
モデル予測制御への応用
それでは今までの議論をまとめて、MPCへの応用を考えていきましょう。基本的に定式化は今までのもので十分なのですが、Stochastic MPC(SMPC)の大きな問題点として、Control StabilityとRecursive feasiblity の二つが良く挙げられます(詳細はHeirung et al. (2018) によく纏まっています)。簡単に言えば、周期的に軌道最適化を解き続ける中で、制御の収束性が数学的に保証しにくい点、そして(特にGaussianのようなunboundedな不確定性パラメータに対して)最適化問題に常に実行可能解がある保証がない、ということです。
特にCovariance Steeringにおいて、ホライズンの終端における共分散行列\Sigma_fと平均値を適切に決めてあげる必要があります。
まず、k-step 目でのMPCの定式化は以下のように表されます。
\begin{aligned}
\min \ & \mathcal{J}(V, K) = \mu_{k+N_p-1|k}^T M \mu_{k+N_p-1|k} + (\mathcal{A}\mu_0 + \mathcal{B} V)^T \bar{Q} (\mathcal{A}\mu_0 + \mathcal{B} V) + V^TRV + \text{tr}[ (\mathbb{I}+\mathcal{B}K)^T \bar{Q} ( ((\mathbb{I}+\mathcal{B}K) + K^T \bar{R} K)\Sigma_Y ]\\
\text{s.t.} \ & \alpha_{x, i}^{T} E_{t-k}\left(\mathcal{A} \mu_{k \mid k}+\mathcal{B} V\right)+\left\|\Sigma_Y^{\frac{1}{2}}(I+\mathcal{B} K)^{T} E_{t-k}^{T} \alpha_{x, i}\right\| \Phi^{-1}\left(1-p_{x, i}\right) \leq \beta_{x, i},\forall j = 0,...,N_s-1 \\
& \alpha_{u, j}^{T} F_{t-k} V+\left\|\Sigma_Y^{\frac{1}{2}} K^{T} F_{t-k}^{T} \alpha_{u, j}\right\| \Phi^{-1}\left(1-p_{u, j}\right)\leq \beta_{u, j}, \forall j = 0,...,N_c-1\\
& E_N\left(\mathcal{A} \mu_{k \mid k}+\mathcal{B} V\right) \in \mathcal{X}_f^\mu, \\
& \Sigma_f \succeq E_N(I+\mathcal{B} K) \Sigma_Y(I+\mathcal{B} K)^{T} E_N^{T}, \\
\text{where} \ & \Sigma_Y = \mathcal{A} \Sigma_{k|k} \mathcal{A}^T + \mathcal{D}\mathcal{D}^T \succ 0 \\
& V=\left[\begin{array}{c}
v_{k \mid k} \\
\vdots \\
v_{k+N_p-1 \mid k}
\end{array}\right], \quad K=\left[\begin{array}{lllll}
K_{k \mid k} & & & & 0 \\
& K_{k+1 \mid k} & & & 0 \\
& & \ddots & & 0 \\
& & & K_{k+N_p-1 \mid k} & 0
\end{array}\right] \\
& \bar{Q} = \tt{blk\_diag}([Q,Q,...,Q, \boldsymbol{0}]) \\
& \bar{R} = \tt{blk\_diag}([R,R,...,R]), \ M \in \mathbb{R}^{n_x\times n_x}
\end{aligned}
変数(\cdot){*|k} , *\in {k, ..., k+N_p -1}は一般に、k-step 目のMPCで最適化される \ast -step目の変数を示しています。行列\bar{Q}が0\sim N_p-2ステップまでの状態に対するコストを(ブロック対角行列の最後が0なのはこのためです)、\bar{R}が制御履歴のコストを、そしてMが終端状態(N_p-1ステップ目)の期待値に対するコストを表現しています。Covariance Steeringの定式化により、ダイナミクスを経た状態が陽に表現できていることで、差分方程式などのダイナミクスが直接制約としては存在しないことに注意してください(Part 1 参照)。
前述したとおり、終端条件\mathcal{X}^{\mu}_fと\Sigma_fをどのように決めるかという話が新規性になります。
Okamoto et al. (2021)では、control stability とrecursive feasibilityの担保をする十分な制御側の導出のために、
\tag{9}
x_{k+1} = (A+B\tilde{K})x_k + Dw_k
のダイナミクス(\tilde{K}はフィードバックゲイン)に対して
\tag{10}
\Sigma = (A+B\tilde{K})\Sigma (A+B\tilde{K})^T + DD^T
を満たすような\Sigmaをassignableな共分散行列と定義して、以下の定理を導出しています。
[定理]
\Sigma_f, \mu_f \in \mathcal{X}_f^\mu, Mに対して、次の3つを仮定する。
(1) \Sigma_f がassignableな行列である。
(2) この時に、Eq. (10)を満たすようなフィードバックゲイン\tilde{K}に対して\mu、
\begin{aligned}
& \alpha_{x, i}^{T} \mu + \left\|\Sigma_Y^{\frac{1}{2}} \alpha_{x, i}\right\| \Phi^{-1}\left(1-p_{x, i}\right) \leq \beta_{x, i},\forall j = 0,...,N_s-1 \\
& \alpha_{u, j}^{T} \tilde{K}\mu + \left\|\Sigma_Y^{\frac{1}{2}} \tilde{K}^{T} \alpha_{u, j}\right\| \Phi^{-1}\left(1-p_{u, j}\right)\leq \beta_{u, j}, \forall j = 0,...,N_c-1\\
& (A +B \tilde{K}) \mu \in \mathcal{X}_f^\mu
\end{aligned}
を満たす。
(3) 終端コスト行列Mは以下の式(離散リアプノフ方程式)を満たす。
(A +B \tilde{K})^T M (A +B \tilde{K}) - M + Q + \tilde{K}^T R \tilde{K} = 0
この時、以下の2点が導かれる。
(i) MPCがk-step目で実行可能解をもつとき、k+n-step目でもMPCの最適化問題が実行可能である。(recursive feasibility)
(ii) ステージコストは上に有界であり、最適解x_{\cdot|k}^{\ast}と u_{\cdot|k}^{\ast} に対して、
\lim _{n \rightarrow \infty} \frac{1}{n} \sum_{t=0}^{n-1} \mathbb{E}_k\left[x_{k+t \mid k}^{* T} Q x_{k+t \mid k}^*+u_{k+t \mid k}^{* T} R u_{k+t \mid k}^*\right] \leq \ell_{\max }
と無限ホライズンでのステージコストが収束するような\ell_{\max}>0が存在する。(control stability)
この定理の証明は非常に重たいので今回の記事では省略します。
ざっくりとした流れは、
(i) feasibility: 制御履歴の最後の制御をu = Ky + vではなく、u = \tilde{K}x^{\ast}のfull-state feedbackの形で表現できる。このような制御履歴で、終端の平均、終端の共分散行列、そして状態/制御に対する線形制約が満たされていることを確認していく
(ii) control stability: x_{k+1|k}から始まる目的関数と、x_{k|k}から始まる目的関数を漸化式として表現し、この差分を不等式として抑える。その後同じ式をk+N-step目まで繰り返し立式し、それを足し合わせることでx_{k+N|k}からの目的関数とx_{k|k}からの目的関数の差分を不等式としてあらわされるようになる。これをn \longrightarrow \infty として極限を取る
という感じです。
自動運転における検証
まず、Okamoto et al. (2021)では、このSMPCアルゴリズムが、Deterministic MPCと比較されています。サーキットを走る自転車の自動運転のアルゴリズムとして採用されています。ダイナミクスは線形化されており、非線形なサーキットにも対応できるようになっています。
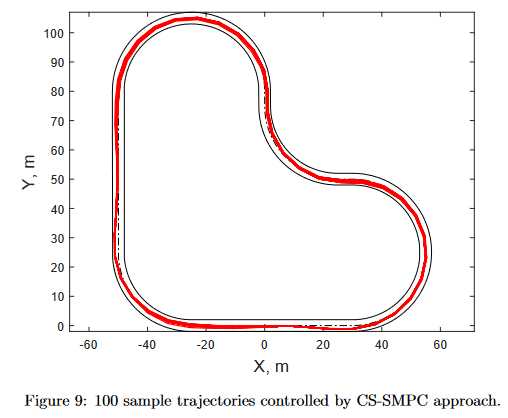
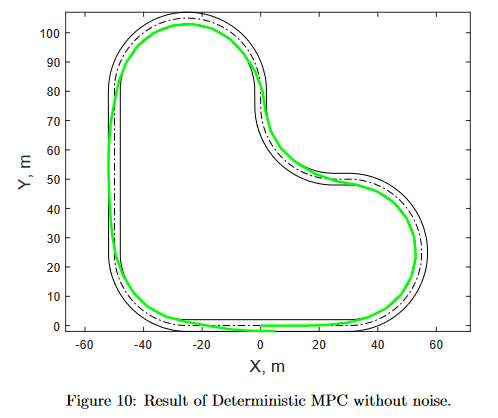
上の画像がダイナミクスにおけるノイズ (w_k) あり環境でのSMPC, 下の画像がノイズなしのMPCです。Deterministic なMPCは、ノイズありの環境では実行可能解を出せず、サーキットを周回できずにアルゴリズムが止まってしまうことが確認されています。
Knaup et al. (2023) では、このアルゴリズムを実際に自動車に乗せて自動運転の試験を行っています。
https://www.youtube.com/watch?v=1ms5fctfAYs
このアルゴリズムの性能が論文ではMPPI(Model Predictive Path Integral control )と比較されており、優位な結果が見られています。(arXiv版がなく残念ながら画像を使えなさそうです。IEEEのサブスクリプションがある方は是非結果を見に行ってみてください!)
Covariance Steeringの長所として、積極的に分散を時間変化させながらコントロールできるところがあります。
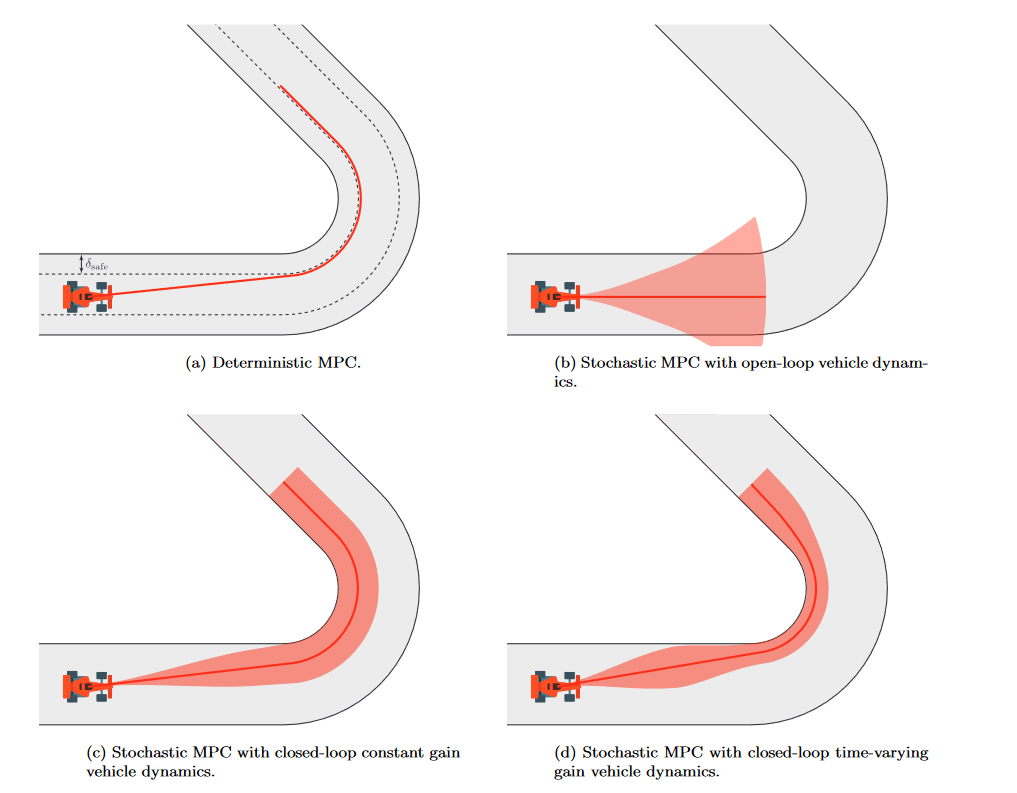
上記画像(Okamoto et al. (2021)より) の右下に描かれているように、路上のカーブになどに応じて分散を広げたり縮めたりするような制御を考えることができ、よりアグレッシブで制約ギリギリを狙えるような制御を作ることができています。通常のStochastic MPCだと、フィードバック制御は各時間における状態のエラーに、LQRなどの事前計算された(i.e., suboptimal な)ゲインKを掛け算して制御を作っているケースが多いです(画像左下)。
終わりに
Covaraince Steering part 2 ということで、確率的な制約を含めたMPCで自動車を走らせるところまでを紹介しました。Covariance Steering は、ほかにもMPPIとの統合(Yin et al. (2022))やADMM を用いたマルチエージェント制御(Saravanos et al. (2021))にも展開されており、まだまだ広がりが期待できる分野です。最適化問題がsemidefinite programming なのはオンボード処理の課題としつつも、確率的/ロバスト最適制御に取り組むうえで、重要な技術になっていきそうな予感がします。
参考文献
- Knaup, J., Okamoto, K. and Tsiotras, P., 2023. Safe high-performance autonomous off-road driving using covariance steering stochastic model predictive control. IEEE Transactions on Control Systems Technology.
- Okamoto, K., 2019. Optimal covariance steering: Theory and its application to autonomous driving (Doctoral dissertation, Ph. D. dissertation, Georgia Institute of Technology).
- Okamoto, K. and Tsiotras, P., 2019. Stochastic model predictive control for constrained linear systems using optimal covariance steering. arXiv preprint arXiv:1905.13296.
- Zhang, Y., Cheng, M., Nan, B. and Li, S., 2023. Stochastic trajectory optimization for 6-DOF spacecraft autonomous rendezvous and docking with nonlinear chance constraints. Acta Astronautica, 208, pp.62-73.
- Heirung, T.A.N., Paulson, J.A., O’Leary, J. and Mesbah, A., 2018. Stochastic model predictive control—how does it work?. Computers & Chemical Engineering, 114, pp.158-170.
- Yin, J., Zhang, Z., Theodorou, E. and Tsiotras, P., 2022, May. Trajectory distribution control for model predictive path integral control using covariance steering. In 2022 International Conference on Robotics and Automation (ICRA) (pp. 1478-1484). IEEE.
- Saravanos, A.D., Tsolovikos, A., Bakolas, E. and Theodorou, E., 2021. Distributed covariance steering with consensus ADMM for stochastic multi-agent systems. Robotics: Systems and Science.



Discussion