本記事はスタンフォード大学の田久保勇志(https://www.linkedin.com/in/yuji-takubo/ )による寄稿です。
はじめに
最適制御における不確定性の考慮(Stochastic Optimal Control) の領域において、ここ5年ほどで大きな注目を集めているCovariance Steeringについて解説をします。
プラント、或いはダイナミクスに対する不確定性(model uncertainty) や状態変数に対する不確定性(state uncertainty)に対する制御手法の歴史はロバスト制御や適応制御 など古くからありますが、この不確定性環境下での最適化(Optimization under uncertainty) から"不確定性を最適化する"(Optimization of Uncertainty) という飛躍を遂げたのがこのCovariance Steering という考え方です。
研究の旨み/革新性
- stochastic linear dynamical system (i.e., diffusion process) において、ノイズ等による分散の変化を特定の値(以下)に終端で抑え込むようなフィードバックゲインを、open-loopの制御側と同時に作ることができる (しかも定式化が極めてシンプル)
- 制約が確定的である場合、 Linear Quadratic Gaussian (LQG)制御との同値性が証明されている
- 制約(path constraint) に確率的な制約(chance constraint) がない場合、平均値の制御(mean steering) と 分散の制御(convarince steering) が分割でき、それぞれが凸最適化問題になる(semidefinite programming, SDP)
- 制約がChance constraintを含む場合でも、(特定の仮定の下で)平均と分散がカップリングしたSDPを作れる
- MPCへの拡張も可能
(欠点: SDP ソルバは線形計画(LP)や二次計画(QP)よりも遅いので、本当にオンボードで処理ができるのかは議論が必要)
問題設定
本記事では細かい証明はスキップし、大きな議論の流れを掴むことを目的としているので、もし興味を持たれた方がいたら、最後の文献をチェックしてみてください。今回はChance constraint やMPC, 状態や制御変数への制約部分には触れず、一番シンプルなCovariance Steeringがどのように行われているかをチェックしていきたいと思います。
まず、次のFinite-horizon discrete-time stochastic linear dynamics を考えます。
x_{k+1} = A_k x_k + B_k u_k + D_k w_k, \quad k = 0, 1, ..., N \tag{1}
ここで、x\in\mathbb{R}^{n_x} (状態変数), u\in\mathbb{R}^{n_u} (制御), w \in \mathbb{R}^{n_w} (単位ホワイトノイズ, \mathcal{N}(0,1.0)) とします。すなわち、このダイナミクスはGaussian Process (diffusion) になります。また、このダイナミクスでは、ノイズが可観測であることを仮定しています。この上で、二次のコストを考慮した最適制御は、次のように書くことができます。
\min \ \mathcal{J} = \mathbb{E} \left[ \sum_{k=0}^{N-1} x_k^T Q_k x_k + u_k^T R_k u_k \right] \\
x_{k+1} = A_k x_k + B_k u_k + D_k w_k, \quad k = 0, 1, ..., N \tag{2}\\
x_0 \sim \mathcal N (\mu_0, \Sigma_0), \quad x_f \sim \mathcal N (\mu_f, \Sigma_f)
ここで、始端/終端の状態が正規分布で表されているという仮定をしています。
問題をキレイにする
ここから、あとで最適化の数学を簡単にするために問題を書き換えていきます。
まず、離散空間におけるN +1個の漸化式の取り扱いが億劫なので、これを一つの超巨大な行列式に落とし込みます。
\tag{3}
X = \mathcal{A}x_0 + \mathcal{B} U + \mathcal{D}W
ここで、拡張した変数は次のように定義されます。
\tag{4}
X = \begin{bmatrix} x_0^T, x_1^T, ... , x_N^T\end{bmatrix}^T, \\
U = \begin{bmatrix} u_0^T, u_1^T, ... , u_N^T\end{bmatrix}^T, \\ W = \begin{bmatrix} w_0^T, w_1^T, ... , w_N^T\end{bmatrix}^T
要は、すべての状態(制御)変数を縦に積んで背の高いベクトルを作っている、ということです。
\mathcal{A}, \mathcal{B}, \mathcal{D}の定義はOkamoto (2019, Ph.D. thesis) の(3.17a) 等を参照してもらえればと思いますが、\mathcal{A}が制御なしのダイナミクスの変化, \mathcal{B}が各時間で入力された制御が、その後のダイナミクスに従っていかに変化するか、最後に\mathcal{G}が各時間で発生したノイズの、その後のダイナミクスに従った変化を司どっています。ある軌道は、(1) 初期値 x_0, (2) 制御履歴 U, (3) ノイズ履歴Wの線形結合で示される、ということがなんとなくわかればOKです!
この状態履歴Xを用いて、平均と分散の履歴も生成できることに注意してください。 \Sigma_X = \mathbb{E}[XX^T] - \mathbb{E}[X]\mathbb{E}[X]^Tとして、
\tag{5}
\mu_0 = E_0 \mathbb{E} [X] , \quad \Sigma_0 = E_0 \Sigma_X E_0^T, \\
\mu_N = E_N \mathbb{E} [X] , \quad \Sigma_N = E_N \Sigma_X E_N^T
が表現できます。E_0, E_N は背の高いベクトルXから、t=0とt=Nの状態を引っ張ってくるような行列です。0と1をいっぱい並べて作れます。
また、目的関数も同様に、大きな行列QとRを作ることで、
\tag{6} \mathcal{J} (X,U) = \mathbb{E}[X^T Q X + U^T R U]
で表現できるのが見えると思います。
いざCovariance Steering
導入部分が長かったですね... いよいよ本命の部分です。最適化をしていきましょう。
まず、次のような制御則を導入します。
\tag{7}
u_k = v_k + K_k y_k, \quad v_k \in \mathbb{R}^{n_u}, \ K_k \in \mathbb{R}^{n_u \times n_x }
ここで、変数y_kは、状態変数におけるノイズの蓄積を示す変数です。次の漸化式を満たします。
\tag{8}
y_{k+1} = A_k y_k + D_k w_k , \quad y_0 = x_0 - \mu_0
すなわち、open-loopの制御v_kと、"平均からのずれ"フィードバックゲインK_kで制御を表現します。
というわけで、例によって例の如くこのベクトルv_kと行列K_kを縦に積んでいき、軌道全体での制御ベクトル/行列 V とK(K_kをブロック対角行列として斜めに置いていくことで作られます), さらにy_kを縦に積んだYを定義して、U = V + KY = V + K (\mathcal{A}y_0 + \mathcal{D}W) を得ることができます。
さて、ここまで長かったですが、漸く嬉しい部分が見えてきます。
(1) まず、これまでに定義してきた変数を用いて、状態変数の平均\bar{X} := \mathbb{E}[X] と、平均からのずれ \hat{X} := X - \mathbb{E}[X]のダイナミクスを分離することができます。
ここで \mu_0 = x_0 - y_0に注意して、
\begin{aligned}
& \bar{X} := \mathbb{E}[X] = \mathcal{A}\mu_0 + \mathcal{B} V \\
& \hat{X} := X - \mathbb{E}[X] = (\mathcal{A}x_0 + \mathcal{B}(KY+V) + \mathcal{D}W) - (\mathcal{A}\mu_0 + \mathcal{B} V) \quad (\because \text{Eq.}(3)) \\
& \quad = \mathcal{A}y_0 + BK (\mathcal{A}y_0 + \mathcal{D} W) + \mathcal{D}W \\
& \quad = (\mathbb{I}+\mathcal{B}K)(\mathcal{A}y_0 + \mathcal{D}W )
\end{aligned}
(2)
\begin{aligned}
& \mathcal{J}(\bar{X}, \hat{X}, V, \bar{U}) = \bar{X}^T Q \bar{X} + \bar{U}^T Q \bar{U} + \text{tr} (Q\mathbb{E} [\hat{X}\hat{X}^T]) + \text{tr} (R\mathbb{E} [\hat{U}\hat{U}^T]) \\
\Leftrightarrow \ & \mathcal{J}(V, K) = (\mathcal{A}\mu_0 + \mathcal{B} V)^T Q (\mathcal{A}\mu_0 + \mathcal{B} V) + V^TRV + \text{tr}[ (\mathbb{I}+\mathcal{B}K)^T Q ( ((\mathbb{I}+\mathcal{B}K) + K^T R K)\Sigma_Y ]\\
& \text{where} \quad \Sigma_Y = \mathcal{A} \Sigma_0 \mathcal{A}^T + \mathcal{D}\mathcal{D}^T \succ 0
\end{aligned}
少し煩雑ですが、大事な部分は2行目の最初の2つの項は V のみの関数、最後のtrace項は K のみの関数ということです。
以上の議論をまとめると、Mean Steering, Covariance Steering の最適化問題は以下のように書くことができます
Mean Steering
\begin{aligned}
\min \ & \mathcal{J}(\textcolor{red}{V}) = (\mathcal{A}\mu_0 + \mathcal{B} \textcolor{red}{V})^T Q (\mathcal{A}\mu_0 + \mathcal{B} \textcolor{red}{V}) + \textcolor{red}{V}^TR \textcolor{red}{V} \\
\text{s.t.} \ & \bar{X} = \mathcal{A}\mu_0 + \mathcal{B} \textcolor{red}{V} \\
& E_0 \bar{X} = \mu_0, \quad E_N \bar{X} = \mu_N
\end{aligned}
これは凸最適化問題になります。
Covariance Steering
\begin{aligned}
\min \ & \mathcal{J}(\textcolor{blue}{K}) = \text{tr}[ (\mathbb{I}+\mathcal{B}\textcolor{blue}{K})^T Q ( ((\mathbb{I}+\mathcal{B}\textcolor{blue}{K}) + \textcolor{blue}{K}^T R \textcolor{blue}{K})\Sigma_Y ] \\
\text{s.t.} \ &
\hat{X} = \mathcal{A}\hat{x}_0 + \mathcal{B} \textcolor{blue}{K} (\mathcal{A}\hat{x}_0 + \mathcal{D}W) + \mathcal{D}W \\
& \Sigma_0 = E_0 \mathbb{E}[\hat{X}\hat{X}^T] E_0^T \\
& \Sigma_N = E_N \mathbb{E}[\hat{X}\hat{X}^T] E_N^T
\end{aligned}
これにて一件落着、と行きたいのですが、最後の\Sigma_Nの制約が二次式の等式制約なので、凸ではありません (分散の初期値はダイナミクスを経験しないの(i.e., K の関数ではないの)で、そのまま最適化ソルバに入れてOK です)。
ですが、現実的な適用を考えると、我々が指定していた終端での分散行列\Sigma_Nよりも、実際の終端での分散が小さい分には困らないので(嬉しいので)、この等式制約を不等式に書き換えることで凸最適化問題を作ります。
\begin{aligned}
& \Sigma_N \succeq E_N \mathbb{E}[\hat{X}\hat{X}^T] E_N^T = E_N(\mathbb{I}+\mathcal{B}K) \Sigma_Y (\mathbb{I}+\mathcal{B}K)^T E_N^T \\
\Leftrightarrow \ & \begin{bmatrix}
\Sigma_N & Z \\
Z^T & \mathbb{I}
\end{bmatrix} \succeq 0 \quad \text{(シュア補行列, semidefinite programmingでよく使います)} \\
& Z := E_N(\mathbb{I}+\mathcal{B}K) \Sigma_Y ^{\frac{1}{2}}
\end{aligned}
というわけで、二つの凸最適化問題ができました!これを解けば無事、不確定性を持つダイナミクスの中で、事前分布x_0 から事後分布x_Nに平均と分散を動かすことができます。
実装してみた
Okamoto (2019, Ph.D. thesis) のAppendixにMATLABでの実装が載っているので、少しこれを改変して、宇宙機のランデブー問題を解いてみます。
Covariance がどのように制御されているかを見るのがこの実装の大きなゴールとし、Chance constriant とMPCの部分に関しては本記事では省略します。
宇宙機の相対運動は、下図のような座標系 (ヒルの座標系)で表され、地球の周りを円形に回る宇宙機の場合、近接する2つの宇宙機の相対的な座標の運動方程式がほぼ線形であることとが知られています。
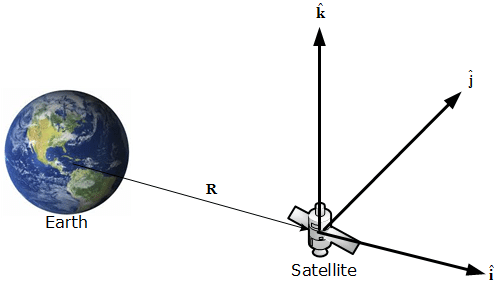
\begin{aligned}
& x_{k+1}
= Ax_k + B u_k + D w_k \\
& x = \begin{bmatrix}
r_x \\ r_y \\ v_x \\ v_y
\end{bmatrix}, \quad u = \begin{bmatrix} \Delta v_y \\ \Delta v_y \end{bmatrix} \\
& A = \begin{bmatrix}
4 - 3\cos(nt) & 0 & \sin(nt)/n & 2(1-\cos(nt))/n \\
6 (\sin(nt)-nt) & 1 & 2(\cos(nt)-1)/n & (4\sin(nt)-3nt)/n \\
3n\sin(nt) & 0 & \cos(nt) & 2 \sin(nt) \\
6n(\cos(nt)-1) & 0 & -2\sin(nt) & 4 \cos(nt) - 3
\end{bmatrix} \\
& B = \begin{bmatrix}
0_{2\times 2} \\ \mathbb{I}_{2\times2}
\end{bmatrix}, \quad D = 0.01 \cdot \mathbb{I}_{4\times4}
\end{aligned}
ここでnは平均運動という宇宙機のもつエネルギーのパラメータで、t はステップの時間幅を示します。今回は各要素にホワイトノイズを独立に加えていきます(w_k = \mathcal{N}(0,1.0) \in \mathbb{R}^4)。
今回の検証で使った初期値は以下の通りです。円軌道の半径は7000km (~高度640km) に設定しました。
\begin{aligned}
\mu_0 &= [0, 1000, 0.0, 1.0]^T [\text{m}, \text{m/s}] \\
\mu_f &= [0, 0, 0, 0]^T [\text{m}, \text{m/s}] \\
\Sigma_0 &= \text{diag}([0.3, 0.3, 0.001, 0.001]) \\
\Sigma_f &= \text{diag}([0.2, 0.2, 0.01, 0.01]) \\
N & = 80, \quad \Delta t = 20 [\text{s}]
\end{aligned}
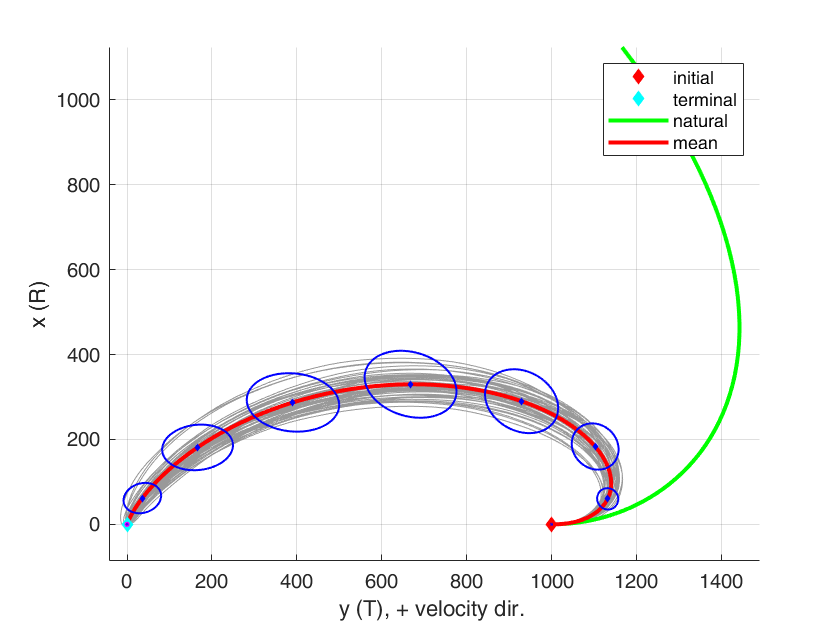
最適化で得られた解を基に、モンテカルロシミュレーションを50回回した結果が下の画像です。灰色の軌道たちがそれぞれの結果、赤の軌道が平均の軌道です。青の楕円が10ステップごとの(x,y)における 3\sigma-error ellipseを示しています。最後に、緑の軌道が制御なしでの軌道を伝播させた結果です。
(慣例的に、ヒルの座標系ではx-方向(地球から離れていく方向を上向きに取ります。x-yが逆転しているのはこのためです。)
図より、初期値から終端にかけて分散の値を守りながら制御されているのが確認できます。
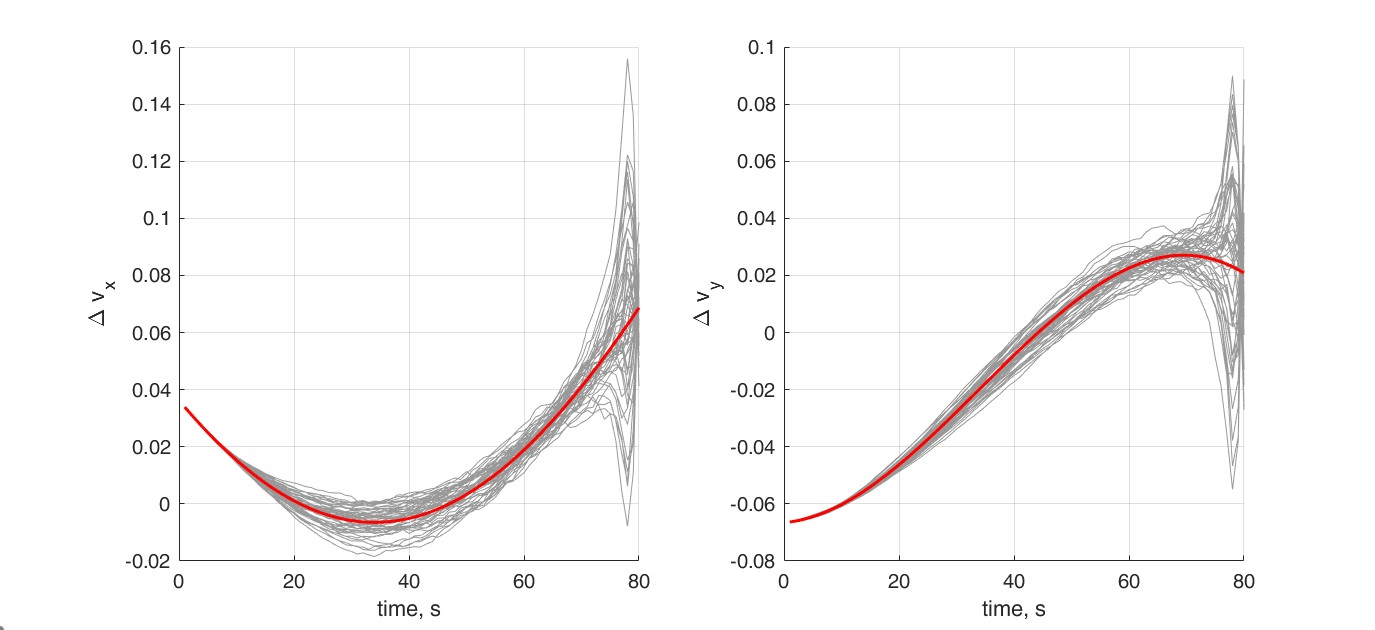
次に制御履歴を見てみましょう。赤が平均の制御Vを示しています。最後の方での制御が大きく広がっていることから、フィードバックゲインK_kがより大きくなっていることで、平均からのズレに対しての制御の分散が広がっている(それによって状態の分散が小さくなっている)ことがわかると思います。
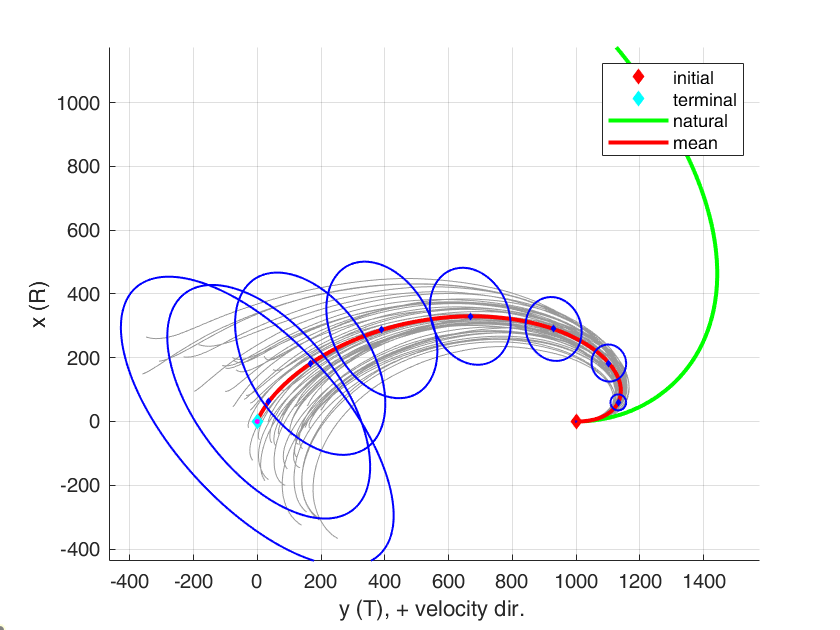
参考までに、Mean steering のみ(フィードバックゲインなし)でのモンテカルロシミュレーションの結果を載せておきます。平均の軌道は全く同じ結果が返ってきていますが、明らかに分散が制御できていないですね。これと結果を比較すると、Covariance steeringの強さが分かっていただけるかと思います。
最後に
今回はCovariance Steeringの触りの部分を解説しました。(文字が多いですが)非常にシンプルな定式化ながら、きれいに凸最適化に落ち着いてくれるところ、そしてControllability を担保できていれば自由な始端・終端の分散や平均を最適制御の制約に入れて最適制御が解けるところのエレガントさを味わってもらえたら幸いです。
最初にも書きましたが、この形はSemidefinite programming で、問題によってはオンボードで安心して使える最適化問題ではないことに注意が必要です。
しかし、慎重なプランニングが必要なケースなどでは効力をかなり発揮してくれるなと個人的には思っています。
Chance constraints やMPCの話はこの上に議論が載ってくる形にもなります。もし機会があればこのあたりの話を Part 2でやるかもです...!
参考文献:
- Goldshtein, Maxim, and Panagiotis Tsiotras. "Finite-horizon covariance control of linear time-varying systems." 2017 IEEE 56th Annual Conference on Decision and Control (CDC). IEEE, 2017.
- Okamoto, Kazuhide, Maxim Goldshtein, and Panagiotis Tsiotras. "Optimal covariance control for stochastic systems under chance constraints." IEEE Control Systems Letters 2.2 (2018): 266-271.
- Okamoto, Kazuhide, and Panagiotis Tsiotras. "Stochastic model predictive control for constrained linear systems using optimal covariance steering." arXiv preprint arXiv:1905.13296 (2019).
- Okamoto, Kazuhide "Optimal covariance steering: Theory and its application to autonomous driving" (Ph.D. thesis), Goergia Institute of Technology (2019)




Discussion