はじめに
名古屋大学医学部 6 年の野村怜史です。本記事では、NeurIPS2018 で発表された論文(GPPVAE)「Gaussian Process Prior Variational Autoencoders」を紹介します。Variational autoencoder (VAE) の事前分布にガウス過程事前分布を導入することを初めて提案した論文です。全データ点間の相関を考慮しつつ、勾配降下法による学習をどのように効率的に行うかの工夫がポイントです。
前回の記事では、多変量時系列データ補間のため VAE の事前分布にガウス過程をおく手法 GP-VAE について紹介しました。GP-VAEでは同一時系列のデータに対してガウス過程事前分布をおいていましたが、本記事で紹介する GPPVAE では全データ点に対してガウス過程事前分布を導入します。こちらも合わせて御覧ください。
モチベーション
通常の VAE では潜在変数 \boldsymbol{z} の事前分布として等方的ガウス分布 \mathcal{N}(\boldsymbol{0}, \boldsymbol{I}) をおくのが一般的であり、各データの潜在変数は独立同分布に従うとの仮定がなされています。しかしながら、現実の問題設定においては、サンプル間相関を考慮したモデリングが重要となることがあります(たとえば時系列の考慮など)。この場合 i.i.d. の仮定は強すぎることが考えられ、データ点間の相関構造のモデリングにより精度向上をはかれるのではないかとの考えが出てきます。そこで、本論文ではガウス過程を事前分布に導入することにより、サンプル間相関を考慮する枠組みを提案しています。
ガウス過程は強力な手法である一方、計算上の課題も出てきます。一つは計算量の問題です。ナイーブにガウス過程を実装・計算しようとすると、総データ点数 N に対し \mathcal{O} (N^3) の計算量が必要となります。そこで、計算量を削減するための工夫が必要となってきます。2つ目は学習方法の問題です。従来の VAE では各データの潜在変数が i.i.d. であるとの仮定があるために、ミニバッチ勾配降下法において勾配の不偏推定量を得ることができていました(ELBO への事前分布の寄与が各データ点の寄与に分解できる)。しかしながら、ガウス過程を導入すると全データ点が依存関係を持つようになるため、ミニバッチ単位での勾配降下法による学習が困難となります。そこで、学習の方法を工夫する必要が出てきます。
GPPVAE ではこれらの問題に対処として (1) カーネル行列の低ランク性の仮定、(2) 損失関数へのガウス過程事前分布の寄与の一次近似、がそれぞれ提案されています。以下、問題を詳しく見ていきます。
GPPVAE
問題設定として、補助データ(e.g. 時刻や姿勢など)つきのサンプル(e.g. 画像)があるとします。この論文では補助データとして object と view の二つを仮定します。特定の object が特定の view で写った画像データを有する、という状況です。たとえば、「数字の 3 (objject) が 30° 回転 (view) した画像」、「ある人 (object) が 45° 斜めを向いている (view) 画像」などです。そして、これらの補助データはそれぞれに対応する特徴ベクトルを有するものとします。(補助データは観測しておらずとも、データから推論することも可能です)
生成モデル
\textit{N} をサンプル数、\textit{P} を object の数、\textit{Q} を view の数とします。また、\lbrace \boldsymbol{y} _n \rbrace _{n=1} ^N を \textit{N} 個のサンプルの \textit{K} 次元ベクトル、\lbrace \boldsymbol{x} _p \rbrace _{p=1} ^P を \textit{P} 個の object の \textit{M} 次元特徴ベクトル、\lbrace \boldsymbol{w} _q \rbrace _{q=1} ^Q を \textit{Q} 個の view の \textit{R} 次元特徴ベクトルとします。そして、\lbrace \boldsymbol{z} _n \rbrace _{n=1} ^N を各データ点の \textit{L} 次元潜在変数ベクトルとします。以下のようなデータ生成過程を考えます。
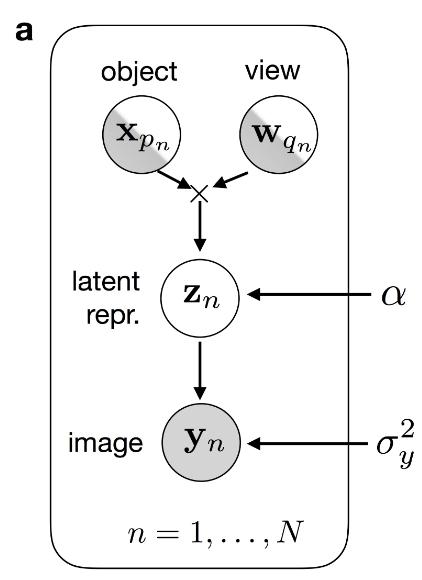
生成モデル(出典:GPPVAE 論文 Figure 1 )。object, view は観測有り/無しの両方の場合を考慮しています。
- object p_n, view q_n である画像の潜在変数 \boldsymbol{z} _n は、関数 f : \mathbb{R}^M \times \mathbb{R}^R \rightarrow \mathbb{R}^L により、object / view の特徴量ベクトル \boldsymbol{x} _{p _n}, \boldsymbol{w} _{q _n} から次式に基づき生成される:
\boldsymbol{z} _n = f( \boldsymbol{x} _{p _n} , \boldsymbol{w} _{q _n}) + \boldsymbol{\eta} _n, \ \text{where} \ \boldsymbol{\eta} _n \sim \mathcal{N} (\boldsymbol{0}, \alpha \boldsymbol{I} _L)
- 画像 \boldsymbol{y} _n は、関数 g : \mathbb{R}^L \rightarrow \mathbb{R}^K により、潜在変数 \boldsymbol{z} _n から次式に基づき生成される:
\boldsymbol{y} _n = g(\boldsymbol{z} _n) + \boldsymbol{\epsilon} _n, \ \text{where} \ \boldsymbol{\epsilon} _n \sim \mathcal{N} (\boldsymbol{0}, \sigma _y ^2 \boldsymbol{I} _K)
ここで、関数 f に対してガウス過程事前分布を仮定します(次節で詳述します)。これにより、object / view の類似度に基づいて潜在変数を得ることができます。関数 g は潜在変数をサンプル空間にマッピングする関数で、VAE のデコーダーとして実装します。
以上の生成モデルのもと、GPPVAE の周辺尤度は次式で表されます。
p(\boldsymbol{Y} | \boldsymbol{X}, \boldsymbol{W}, \boldsymbol{\phi}, \sigma _y ^2, \boldsymbol{\theta}, \alpha)
= \int p(\boldsymbol{Y} | \boldsymbol{Z}, \boldsymbol{\phi}, \sigma _y ^2) p(\boldsymbol{Z} | \boldsymbol{X}, \boldsymbol{W}, \boldsymbol{\theta}, \alpha) \ d \boldsymbol{Z}
ここで、\boldsymbol{Y} = [\boldsymbol{y} _1 , ..., \boldsymbol{y} _N] ^T \in \mathbb{R} ^ {N \times K}, \boldsymbol{Z} = [\boldsymbol{z} _1 , ..., \boldsymbol{z} _N] ^T \in \mathbb{R} ^ {N \times L}, \boldsymbol{W} = [\boldsymbol{w} _1 , ..., \boldsymbol{w} _Q] ^T \in \mathbb{R} ^ {Q \times R}, \boldsymbol{X} = [\boldsymbol{x} _1 , ..., \boldsymbol{x} _P] ^T \in \mathbb{R} ^ {P \times M} です。\boldsymbol{\phi} は関数 g (デコーダー)のパラメータ、\boldsymbol{\theta} は GP カーネルのパラメータです。
ガウス過程モデル
前節で、関数 f に対してガウス過程事前分布を仮定すると述べました。具体的には、全データにわたる潜在変数 \boldsymbol{Z} \in \mathbb{R} ^ {N \times L} の各列 \boldsymbol{z} ^l \in \mathbb{R} ^L が多変量正規分布に従うと仮定し、object と view の類似度に基づいて潜在表現が得られると考えます。
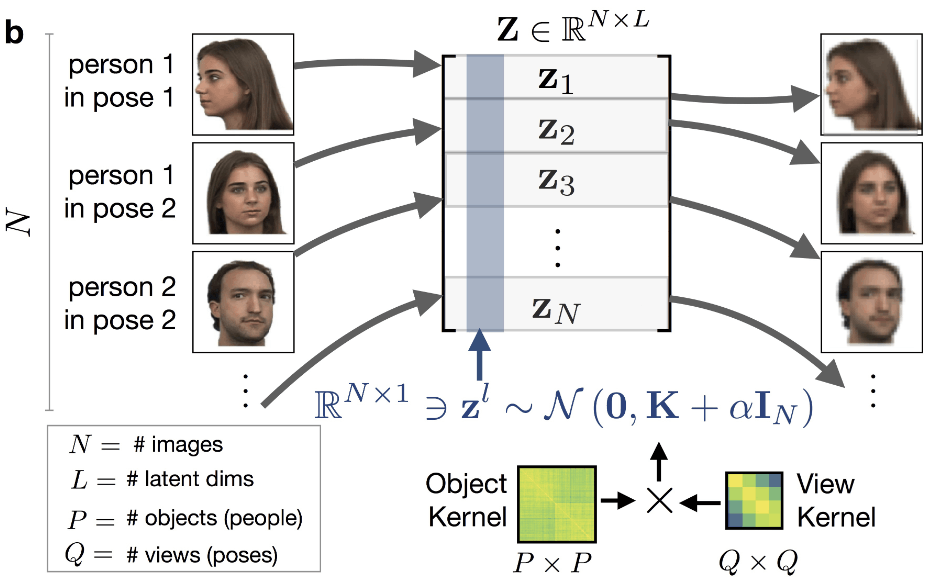
ガウス過程モデル(出典:GPPVAE 論文 Figure 1)
つまり
p(\boldsymbol{Z} | \boldsymbol{X}, \boldsymbol{W}, \boldsymbol{\theta}, \alpha) = \prod _{l=1} ^L \mathcal{N} (\boldsymbol{z} ^l | \boldsymbol{0} , \boldsymbol{K} _ {\boldsymbol{\theta} } (\boldsymbol{X}, \boldsymbol{W}) + \alpha \boldsymbol{I} _N )
と仮定します。共分散関数 \boldsymbol{K} _ {\boldsymbol{\theta} } (\boldsymbol{X}, \boldsymbol{W}) は view 同士の相関を考慮する view カーネル、及び object 同士の相関を考慮する object カーネルで構成します。サンプル n, m の共分散は次式で与えられるとします。
\boldsymbol{K} _ {\boldsymbol{\theta} } (\boldsymbol{X}, \boldsymbol{W}) _{nm} = \mathcal{K} _{\boldsymbol{\theta}} ^{(view)} (\boldsymbol{w} _{q_n}, \boldsymbol{w} _{q_m}) \ \mathcal{K} _{\boldsymbol{\theta}} ^{(object)} (\boldsymbol{x} _{p_n}, \boldsymbol{x} _{p_m})
view / object の特徴量ベクトルが観測されていない場合は、未観測の特徴量ベクトルを潜在変数として扱い点推定量を得ることで対処します。この場合、データ点に対応した潜在変数を保持しておき、勾配降下法により更新することで求めます。
推論モデル
潜在変数 \boldsymbol{z} _n の事後分布を解析的に計算することは困難であるため、変分推論により近似事後分布を得ることを考えます。通常の VAE と同様、factorized Gaussian を近似分布として仮定し、平均/分散パラメータをエンコーダにより推論します:
q _{\boldsymbol{\psi}} (\boldsymbol{Z} | \boldsymbol{Y}) = \prod _{n} \mathcal{N} (\boldsymbol{z} _n | \boldsymbol{\mu} _{\boldsymbol{\psi} } ^z (\boldsymbol{y} _n), \text{diag}
( {\boldsymbol{\sigma}^z}^2 _{\boldsymbol{\psi}} (\boldsymbol{y} _n) )
$\boldsymbol{\psi} $ はエンコーダのパラメータです。このとき、対数周辺尤度の変分下限(ELBO)は次式で表されます(導出はサプリで丁寧に記載されていますので割愛します)。
\begin{aligned}
\log p(\boldsymbol{Y} | \boldsymbol{X}, \boldsymbol{W}, \boldsymbol{\phi}, \sigma _y ^2, \boldsymbol{\theta}, \alpha) \geq \ &
\mathbb{E} _{\boldsymbol{Z} \sim q _{\boldsymbol{\psi}}} \Big\lbrack \sum _n \log \mathcal{N} (\boldsymbol{y} _n | g _{\boldsymbol{\phi}} (\boldsymbol{z} _n), \sigma _y ^2 \boldsymbol{I} _{K} ) + \log p(\boldsymbol{Z} | \boldsymbol{X}, \boldsymbol{W}, \boldsymbol{\theta}, \alpha) \Big \rbrack \\\ & \ + \frac{1}{2} \sum _{nl} \log ( {\boldsymbol{\sigma}^z}^2 _{\boldsymbol{\psi}} (\boldsymbol{y} _n)_l) + \text{const.}
\end{aligned}
学習は ELBO を最大化することで行います。これは、次式で表される損失関数(-ELBO)を最小化することに等しいです。
l(\boldsymbol{\phi}, \boldsymbol{\psi}, \boldsymbol{\theta}, \alpha, \sigma _y ^2) = NK \log \sigma_y ^2+ \sum _n \frac{\lVert \boldsymbol{y} _n - g _{\phi} (\boldsymbol{z} _{\boldsymbol{\psi}_n}) \rVert ^2}{2 \sigma_y ^2} - \log p(\boldsymbol{Z} _{\boldsymbol{\psi}} | \boldsymbol{X}, \boldsymbol{W}, \boldsymbol{\theta}, \alpha) + \frac{1}{2} \sum _{nl} \log ( {\boldsymbol{\sigma}^z}^2 _{\boldsymbol{\psi}} (\boldsymbol{y} _n)_l)
ここで \boldsymbol{Z} _{\boldsymbol{\psi}} = [\boldsymbol{z} _{\boldsymbol{}\psi 1}, ..., \boldsymbol{z} _{\boldsymbol{\psi} _N}] \in \mathbb{R} ^ {N \times L} は変分事後分布 q _{\boldsymbol{\psi}} からのサンプルで、通常の VAE と同様 re-parametrization trick を用いてサンプリングします。
損失関数の最小化を行うにあたり、本モデル特有の問題点が二点浮上してきます。一つ目は、ガウス過程事前分布を仮定しているため、(ナイーブに計算を行おうとすると)データ点数の三乗のオーダーの計算コストが必要となる点です。2つ目は、ガウス過程事前分布の尤度項を計算する際に全データ点を必要とするため、ミニバッチ勾配降下法が適用できない点です。次節でこれらの問題への対処法を説明します。
モデルの学習
本セクションが本論文の核心です。損失関数にガウス過程事前分布が含まれているため、二つの問題が生じてしまうことを前節で述べました。つまり、(1) 全データ点に依存するカーネル行列(の逆行列および行列式)の計算コストがデータ点数 N に対し \mathcal{O} (N^3) であること、(2) ガウス過程事前分布の尤度計算に全データを必要とするためミニバッチ勾配降下法が適用できないこと、です。これらの問題への対処として、(1) カーネル行列の低ランク性の仮定、(2) 損失関数へのガウス過程事前分布の寄与を一次近似すること、がそれぞれ提案されています。以下、それぞれについて説明します。
まず、一つ目の問題点に対する対処です。ここでは、カーネル行列の低ランク性を仮定することにより、ガウス過程の計算コストをデータ点数 N に対して線形のオーダーに抑えます。つまり、低ランク行列 \boldsymbol{V} \in \mathbb{R}^{N \times H} (H \ll N) を用い、全体の分散共分散行列が \boldsymbol{K} = \boldsymbol{V} \boldsymbol{V}^T + \alpha \boldsymbol{I} と表せるとします。後述しますが、本手法の学習過程において逆行列 \boldsymbol{K} ^{-1} を含む計算は、何らかの行列との積の形で出てきます。これは、任意の行列を \boldsymbol{M} \in \mathbb{R} ^ {N \times K} で表すとすると、Woodbury の恒等式から
\boldsymbol{K}^{-1} \boldsymbol{M} = \frac{1}{\alpha} \boldsymbol{I} - \frac{1}{\alpha} \boldsymbol{V} (\alpha \boldsymbol{I} + \boldsymbol{V}^T \boldsymbol{V}) ^{-1} \boldsymbol{V} ^T \boldsymbol{M}
として計算できます。上式の計算コストは \mathcal{O} (NH^2 + H^3 + HNK) であり、データ点数 N に対して線形のオーダーで計算できることがわかります。
次に、二つ目の問題点(ガウス過程事前分布の尤度計算に全データを必要とするためミニバッチ勾配降下法が適用できない)についてです。まず、問題を具体的に把握してみます。ガウス過程事前分布は潜在空間の次元方向に独立性を仮定しているため
p(\boldsymbol{Z} _{\boldsymbol{\psi}} | \boldsymbol{X}, \boldsymbol{W}, \boldsymbol{\theta}, \alpha) = \prod _{l=1} ^L \mathcal{N} (\boldsymbol{z}_l | \boldsymbol{0}, \boldsymbol{K})
と分解できます。そのため、ガウス過程事前分布のある次元 l における対数尤度は、\boldsymbol{z} _{\psi} \in \mathbb{R} ^N として
\log p(\boldsymbol{z} _{\boldsymbol{\psi}} | \boldsymbol{X}, \boldsymbol{W}, \boldsymbol{\theta}, \alpha) = -\frac{1}{2} \boldsymbol{z} _{\boldsymbol{\psi}} ^T \boldsymbol{K} ^{-1} \boldsymbol{z} _{\boldsymbol{\psi}} - \frac{1}{2} \log |\boldsymbol{K}| + \text{const.} \tag{1}
です。\boldsymbol{z} _{\psi} は全データ点を含み、また \boldsymbol{K} の計算には全データ点を必要とするため、この項を計算するだけでもそれなりの計算コストが必要です。ですが、ここで何よりも問題となるのは、上式が各データ点の寄与に分解できないことです。勾配が各データ点の寄与に分解できないため、誤差逆伝播法で学習する場合、全データをメモリにロードした上で上式の値を評価することが必要となりますが、これは現実的に困難です。
そこで、ガウス過程事前分布の損失関数への寄与を一次近似することにより、この問題に対処します。この近似により、損失関数を各データ点の寄与に分解できるようになるのがポイントです。いま、ガウス過程事前分布の尤度項計算に関わるパラメータを \boldsymbol{\xi} = \lbrace \boldsymbol{\psi} , \boldsymbol{\theta}, \alpha \rbrace とおきます(それぞれ VAE のエンコーダ、カーネル、ガウス過程のノイズスケールのパラメータです)。そして式 (1) をパラメータの汎関数の形 f(\boldsymbol{z} (\boldsymbol{\xi}), \boldsymbol{V} (\boldsymbol{\xi}), \alpha (\boldsymbol{\xi})) で表現します。汎関数 f(\boldsymbol{z} (\boldsymbol{\xi}), \boldsymbol{V} (\boldsymbol{\xi}), \alpha (\boldsymbol{\xi})) を現在のパラメータの値 (\boldsymbol{z} (\boldsymbol{\xi}_0), \boldsymbol{V} (\boldsymbol{\xi}_0), \alpha (\boldsymbol{\xi}_0)) の周りでテイラー展開すると
f(\boldsymbol{z} (\boldsymbol{\xi}), \boldsymbol{V} (\boldsymbol{\xi}), \alpha (\boldsymbol{\xi})) \approx \boldsymbol{a} ^T \boldsymbol{z} (\boldsymbol{\xi}) + \text{tr} (\boldsymbol{B}^T \boldsymbol{V} (\boldsymbol{\xi}) + c \alpha (\boldsymbol{\xi})) + \text{const.} \tag{2}
となります。ここで
\begin{aligned}
\boldsymbol{a} & = & \left(\frac{\partial f}{ \partial \boldsymbol{z} }\right)_{\boldsymbol{\xi}_0} \\
\boldsymbol{B} &=& \left( \frac{\partial f}{ \partial \boldsymbol{V} } \right) _{\boldsymbol{\xi}_0} &=& (-\boldsymbol{K}^{-1} \boldsymbol{z} \boldsymbol{z} ^T \boldsymbol{K}^{-1} \boldsymbol{V} + \boldsymbol{K}^{-1} \boldsymbol{V} ) _{\boldsymbol{\xi}_0} \\
c &=& \left( \frac{\partial f}{ \partial \alpha } \right)_{\boldsymbol{\xi}_0} &=& \frac{1}{2} (- \boldsymbol{z}^T \boldsymbol{K}^{-1} \boldsymbol{K}^{-1} \boldsymbol{z} + \text{tr} ( \boldsymbol{K}^{-1}) )_{\boldsymbol{\xi}_0}
\end{aligned}
とおきました。実際、式 (2) 右辺の第一項、第二項は
\sum _{n=1} ^N \left\{ (\frac{\partial f}{ \partial z_n}) _{\boldsymbol{\xi} _0 } z_n (\boldsymbol{\xi}) + \sum _{h=1}^H (\frac{\partial f}{ \partial V _{nh}}) _{\boldsymbol{\xi} _0 } V _{nh} (\boldsymbol{\xi}) \right\}
のように、各データ点 n の和として表すことができます。したがって、テイラー展開の係数項を全データ点を用いてあらかじめ計算しておけば、上記の二項をミニバッチ単位で計算し勾配を足し合わせることが可能です。
実際の学習は、以下の四段階からなる full gradient descent により行います。
(1) エンコーダー + re-parametrization trick を用い、ミニバッチ単位で潜在変数 \boldsymbol{z} の推論を行う。 このとき、潜在変数 \boldsymbol{z} は全データ分を保持しておく。
(2) 全データ点の潜在変数 \boldsymbol{z} を用い、テイラー展開の係数 \boldsymbol{a}, \boldsymbol{B}, c を計算する。
(3) ミニバッチごとに損失関数の計算を行い、勾配を計算する。この際、ガウス過程事前分布の尤度項の損失関数への寄与は式 (2) に置き換えて計算する。
(4) 全データの勾配を足し合わせ、勾配降下法によりパラメータの更新を行う。
out-of-sample の予測
モデルの訓練後、未知のデータ点 \boldsymbol{y} _{\star} に対する予測は以下の予測事後分布に基づいて行います。ただし、予測したいデータ点 \boldsymbol{y} _{\star} に対応する object p _{\star}, view q _{\star} (及び対応するそれぞれの特徴量ベクトル \boldsymbol {x } _{\star}, \boldsymbol{w} _{\star}) は指定して与えるものとします。また、\boldsymbol{y} _{\star} に対応する潜在変数を \boldsymbol{z} _{\star} で表すものとします。
p ( \boldsymbol{y} _{\star} | \boldsymbol{x} _{\star}, \boldsymbol{w} _{\star}, \boldsymbol{Y}, \boldsymbol{X}, \boldsymbol{W} ) \approx \int p (\boldsymbol{y} _{\star} | \boldsymbol{z} _{\star}) p(\boldsymbol{z} _{\star} | \boldsymbol{x} _{\star} , \boldsymbol{w} _{\star}, \boldsymbol{Z}, \boldsymbol{X}, \boldsymbol{W}) q(\boldsymbol{Z} | \boldsymbol{Y} ) d \boldsymbol{z} _{\star} d \boldsymbol{Z}
訓練データの潜在変数 \boldsymbol{Z} の事後分布 p(\boldsymbol{Z} | \boldsymbol{Y}) を変分事後分布 q(\boldsymbol{Z} | \boldsymbol{Y}) に置き換えて予測分布を近似するのがポイントです。実際の予測は以下の三段階で行います。
(1) 訓練データ点をエンコーダで埋込み変分事後分布 q(\boldsymbol{Z} | \boldsymbol{Y}) を計算する
(2) ガウス過程予測事後分布 p(\boldsymbol{z} _{\star} | \boldsymbol{x} _{\star} , \boldsymbol{w} _{\star}, \boldsymbol{Z}, \boldsymbol{X}, \boldsymbol{W}) に基づいて潜在変数 \boldsymbol{z} _{\star} を計算する
(3) 潜在変数 \boldsymbol{z} _{\star} をデコーダへの入力として \boldsymbol{y} _{\star} を出力する
実験結果
今回、以下の 4 つのモデルを用いて実験を行っています。CVAE 及び LIVAE はベースライン手法です。
- GPPVAE with joint optimization (GPPVAE-joint):「VAE のみで学習 → ガウス過程パラメータのみ学習 → VAE + ガウス過程の全体で学習」の三段階で学習を行う。
- GPPVAE with disjoint optimization (GPPVAE-dis):「VAE のみで学習 → ガウス過程パラメータのみ学習」の二段階で学習を行う。GPPVAE-joint とは異なり全体での学習は行わない。
- Conditional VAE (CVAE):補助データの特徴ベクトルをエンコーダ・デコーダの入力に concatenate して学習を行う。out of sample の予測では、object の特徴量ベクトルには学習データ中に含まれる対象 object のデータの平均を与える。
- Linear Interpolation in VAE latent space (LIVAE):通常の VAE で学習を行う。out-of-distribution の予測は、対象 object の二つの angle を表す潜在変数の間を線形補間することにより行う。
Rotated MNIST
一つ目の実験は、MNIST データを対象としています。まず、学習に使用するデータについてです。 MNIST の数字の 3 を用い、角度を指定して回転させることでデータを生成します。角度は [0, 2 \pi ) を 16 等分割しています。今回、全部で N = 6,400 枚の画像を用いています。学習時には一つの角度に対応する画像を取り除き、out-of-distribution の予測検証に用います。
訓練時、view feature vector はデータ生成時に指定した角度を与えます。object feature vector はデータから学習させます。カーネルは以下を使用します。
\boldsymbol{K} _{\boldsymbol{\theta}} ( \boldsymbol{X}, \boldsymbol{w} ) _{nm} = \beta \exp \left( - \frac{2 \sin ^2 | w _{q_n} - w _{q_m} |}{ \nu ^2} \right) \boldsymbol{x} _{p_n} ^T \boldsymbol{x} _{p_m}
結果の図を以下に示します。 MSE では提案手法 GPPVAE-joint が最も小さい値をとっており、高い性能を発揮していることがわかります (\boldsymbol{\text{a}})。\boldsymbol{\text{b}}, \boldsymbol{\text{c}} では、変分事後分布のパラメータの平均・分散の分布を、 VAE とGPPVAE で比較しています。VAE に比べて GPPVAE はより尖った分布となっており、潜在変数の各次元の情報が必要最低限に抑えられていることを示唆します。\boldsymbol{\text{d}} は訓練データに含まれない角度の予測 (out-of-distribution prediction) です。CVAE や LIVAE と比較して GPPVAE では数字画像を正確に、所望の角度で予測できており、ガウス過程事前分布をおくことの有用性を示す結果です。
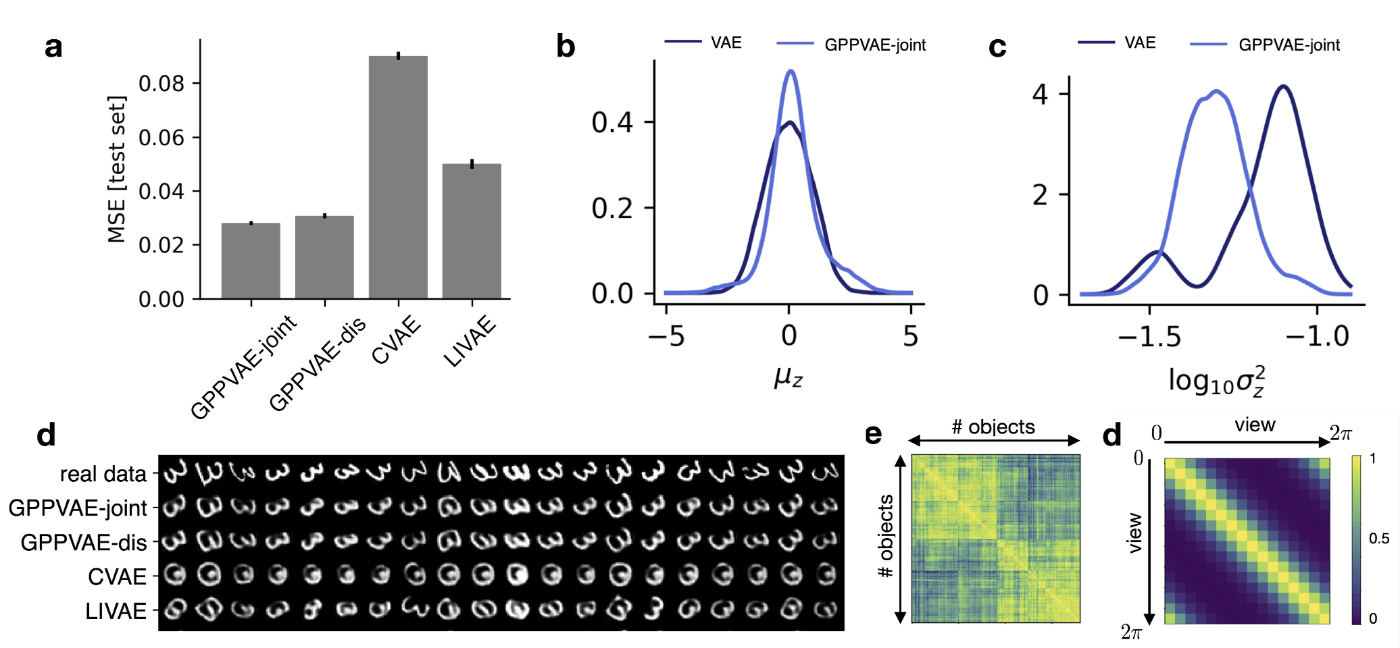
Rotated MNIST に対する結果(出典:GPPVAE 論文 Figure 2 )
Face dataset
2つ目の実験は、Face-Place Database (3.0) のデータを対象としています。様々な人 (object) の顔が様々な角度 (view) で写った画像のデータセットです。こちらの実験では object, view 双方の特徴ベクトルが未観測であるため、こちらもあわせて学習を行います。Out-of-distribution prediction においては、学習データに含まれていたある人物 (object) について、未観測の角度 (view) の画像を予測させます。
結果の図を以下に示します。MSE の観点では GPPVAE が最も良い性能を示しています (\boldsymbol{\text{a}})。\boldsymbol{\text{b}} では、CVAE や LIVAE では人/角度が別物になってしまうことがあるのに対し、GPPVAE では人/角度をある程度正しく予測できています。人物 (object) と角度 (angle) の相関を別々に考慮して学習できていることを示唆する結果です。
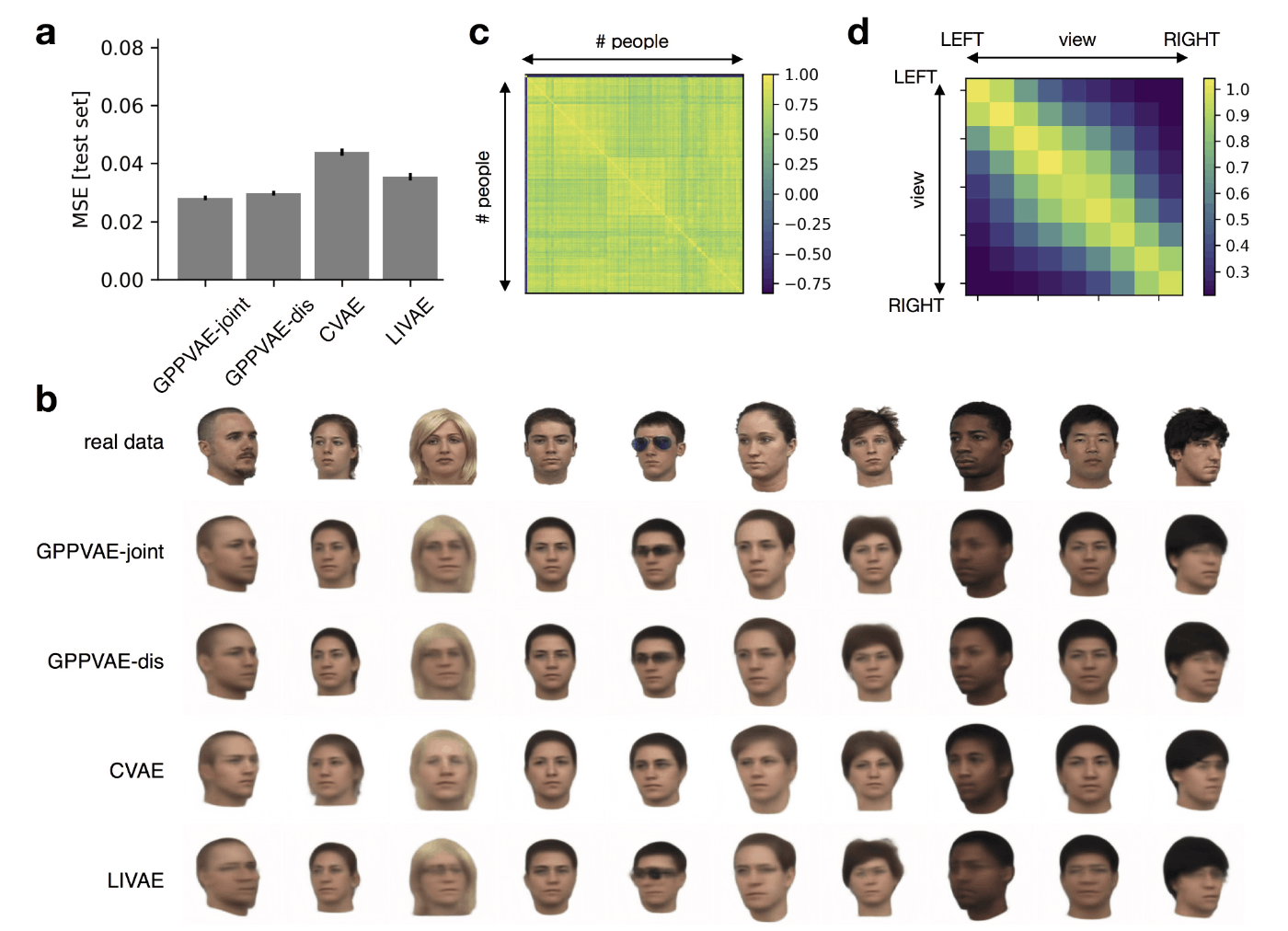
Face dataset に対する結果(出典:GPPVAE 論文 Figure 3)
まとめ
本記事では、VAE の事前分布にガウス過程をおいたモデル GPPVAE を紹介しました。構造としては、VAE の潜在変数に対してガウス過程潜在変数モデル (GPLVM) を適用したような形となっています。サンプル間の相関構造を考慮した潜在変数をモデリングすることで、従来手法と比べてより高い精度での予測を可能とした他、view を指定した条件付き生成においても有望な結果が得られています。Disentanglement / counterfactual generation のための方法としてこの方向性は興味深く、ドメインに応じたカーネル関数の設計を行うことで様々なアプリケーションが考えられそうです。
たとえば今回、実験ではタスクとして「訓練中に観測した object について、観測していない view での画像を予測する」ことを行っています。これを達成するため、view カーネルは角度を捉えられるようにきちんと設計をしつつ、それ以外の情報は object kernel (線形カーネル)にまとめて吸収させています。これは view カーネルでほしい情報 (view) だけを disentangle して抽出し、それ以外の情報を object feature vector に詰め込んで特徴量抽出を行っている、という見方ができます。
このように、データから抽出したい情報を、カーネル関数の設計を通じて反映させることが可能な点に本手法の旨味があるように思います。VAE の事前分布を設計するVampPriorのような手法とは異なるポイントです。
一方で、本手法には限界点も存在します。まず、ガウス過程項の計算が全データ点に依存するため、パラメータ更新には full gradient による勾配降下法を必要とし、ミニバッチ勾配降下法を適用できない点です。これにより学習が困難となる可能性が考えられます。実際、提案された学習方法を用いた本論文における実験は「通常の VAE のみで学習 → カーネル関数のみ学習 → full gradient でまとめて学習」の三段階を採用しており、full gradient のみでは学習が困難であったことが想像されます。またガウス過程項の計算について、低次元の潜在変数を用いて計算を行っているとはいえ、大規模なデータセットの場合に全潜在変数をメモリに載せることは困難になりえます。
次回は、特に2つ目の限界点に対し、誘導点 (inducing points) を用いてガウス過程事前分布の計算を効率化した VAE について紹介したいと思います。




Discussion