欠損値を含む多変量時系列データを補完する手法「GP-VAE」

はじめに

Proxima Technology にて論文読みバイトをさせて頂いております、名古屋大学医学部5年の野村怜史です。大学では生命科学分野での機械学習手法の研究開発を行っています。

本記事では、AISTATS 2020 で発表された論文「GP-VAE: Deep Probabilistic Time Series Imputation」を紹介します。この論文では、欠損値を含む多変量時系列データを対象とし、欠損値補間を行うための手法 GP-VAE を提案しています。Variational autoencoder (VAE) を用い、次元削減と潜在空間におけるガウス過程の導入を両立している点がポイントです。

モチベーション

本手法は、多変量時系列データにおける欠損値補間を問題とします。ここでは、チャネル（特徴量）方向・時間方向の双方における相関関係を考慮しつつ欠損値補間を行いたい、という問題意識があります。これら2つを同時に考慮できる枠組みはこれまであまり提案されてきませんでした。たとえば 、欠損値補間で慣習的に用いられてきた前方補間（一時刻前の観測値で欠損値を補間）や平均値補間（観測の平均値で欠損値を補間）だと、チャネル（特徴量）間の相関関係をうまく捉えることができません。また、VAE のような非線形次元削減と補間を同時に行う手法では、チャネル（特徴量）方向の相関は捉えられる一方で時間方向の相関を捉えることはできません。

これに対し、ガウス過程は多変量時系列モデリングにおいて強力な枠組みであり、チャネル（特徴量）方向・時間方向の双方における相関関係を考慮することが可能です。完全データ（特徴量方向には欠損がない）が対象であれば、たとえば欠損時刻点における補間を精度高く行うことができます。しかしながら不完全データ（特徴量欠損あり）の場合、ガウス過程をそのまま適用することは困難です。

そこで、次元削減と時系列モデリングを同時に行おうという発想が出てきます。つまり、次元削減によりチャネル（特徴量）間の相関関係を考慮しつつ、完全データである低次元潜在変数を用いて時系列方向の相関を考慮しようという発想です。さらに、（非線形）次元削減と時系列モデリングを微分可能な枠組みにより end-to-end で同時に学習させることで、両者のモデリングにとって望ましい推論が可能となることが期待されます。

提案手法では VAE を基盤のモデルとして用いています。VAE を選ぶモチベーションとしては、非線形次元削減・潜在空間における時系列モデリングを同時に可能とする枠組みである点が挙げられます。VAE は深層学習を用いた変分推論を行うための汎用的枠組みとして捉えることもでき、設計する確率モデルに応じた柔軟な推論を可能とするため、今回のようなモデリングにも相性が良いと考えられます。

問題設定

$T$ 個の連続する各時刻点において $d$ 次元の観測を有するデータ $\mathbf{X} \in\mathbb{R}^{T \times d}$ を考えます。ある時刻点 $t$ におけるデータは $\mathbf {x_t} = [x_{t1}, ..., x_{tj}, ..., x_{td}]^{\top} \in\mathbb{R}^{d}$ です。
また、データ点のある要素が欠損しているような状況を考えます。データ点 $\mathbf{x}_t$ のうち観測された特徴量を $\mathbf{x}_t^o := \lbrack x _{tj} |x _{tj} \rm{ \ is \ observed}\rbrack$、観測されていない特徴量を $\mathbf{x}_t^m := \lbrack x _{tj} |x _{tj} \rm{ \ is \ missing}\rbrack$ とします。$\mathbf{x}_t^o \cup \mathbf{x}_t^m \equiv \mathbf{x}_t$ です。

欠損値補完の問題は、観測特徴量 $\mathbf{X}^o := [ \mathbf{x} _t ^o] _{1:T}$ が与えられたもとで、欠損特徴量 $\mathbf{X}^m := [ \mathbf{x} _t ^m] _{1:T}$ の真の値を推定する問題です。つまり、 $p(\mathbf{x} _t^m | \mathbf{x} _{1:T}^o)$ を推定することとなります。時系列データゆえに観測の全時刻点 ($1:T$) が条件に含まれている点がポイントです。

GP-VAE

欠損値補間は、多変量時系列データの次元間の相関構造・時点間の相関構造の両者を考慮した上でなされるのが望ましいです。そこで GP-VAE では、(1) VAE のエンコーダーを用いた観測データの非線形な次元削減、 (2) 潜在空間（次元削減した低次元空間）におけるガウス過程を用いた時系列モデリング、の２つを同時に行います。

(1) の次元削減を VAE の枠組みで行うことにより、同一時刻点における次元間の相関を捉えた潜在変数の推論を可能とします。また、(2) の潜在空間における時系列モデリングを行うことにより、欠損値に左右されることなしに、データの時点間にわたる相関構造を捉えることを可能とします。VAE により推定される潜在変数は全次元が fully determined であるため、（欠損値を有するデータへの適用が困難である）ガウス過程のような手法を適用することができます。

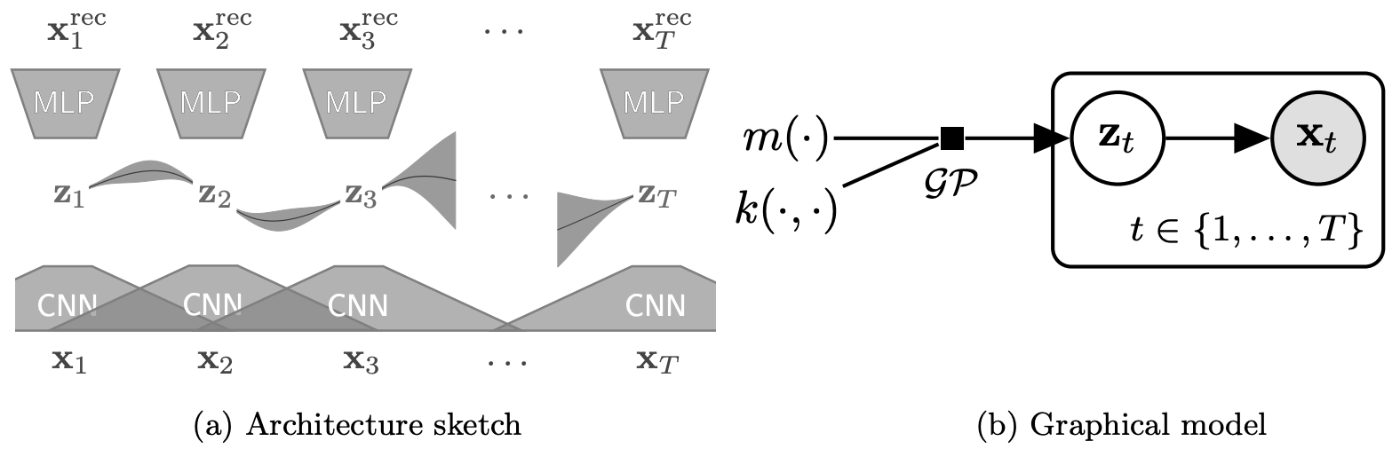
GP-VAE モデル概要 出典：GP-VAE 論文 Figure 1

生成モデル

各時刻における観測 $\mathbf{x}_t$ に対し、対応する潜在変数 $\mathbf{z}_t \in \mathbb{R}^k$ を考えます。ここで $k$ は潜在変数の次元です。そして、この潜在変数 $\mathbf{z}_t$ はガウス過程に従うと考えます。つまり

$$\mathbf{z} _t \sim \mathcal{GP} (m _z( \cdot ), k_z(\cdot , \cdot))$$

です。

$\mathbf{x} _t$ の観測分布にガウス分布を仮定し、潜在変数の時系列 $\mathbf{z} _{1:T}$ が与えられたとき、時点ごとに

$$p _ {\theta} (\mathbf{x} _t | \mathbf{z _t}) = \mathcal{N} (g _{\theta} (\mathbf{z} _t), \sigma^2 \mathbf{I})$$

と生成されると考えます。$g _{\theta}(\cdot)$ はパラメータ$\theta$ によってパラメトライズされる非線形関数で、本モデルではニューラルネットワークによりモデリングします。VAE のデコーダーに相当するものです。

多変量時系列データモデリングの難しさの一つとして、データ変動が複数のタイムスケールで認められることを著者らは指摘しています。これに対し、ガウス過程で一般的に用いられるカーネル、例えば RBF カーネル $k_{RBF} = \exp (- \lambda r^2 / 2)$を用いると、単一のタイムスケールしか考慮することができません。そこで、複数タイムスケールを考慮できるカーネルとして Cauchy カーネルをガウス過程事前分布に用いることを提案しています。

$$k _{Cau} (\tau, \tau^{'}) = \sigma^2 ( 1 + \frac{(\tau - \tau^{'}) ^2} {l^2} )^{-1}$$

$\tau, \tau^{'}$ は観測時刻点を表します。これは、RBF カーネルのスケールパラメータ $\lambda$ にガンマ分布を仮定 $p(\lambda|\alpha, \beta) \propto \lambda^{\alpha-1} \exp(- \alpha \lambda / \beta)$ し、$\lambda$ を積分除去することにより得られる Rational Quadratic kernel の特殊な場合に相当します。つまり

$$\int p(\lambda|\alpha, \beta) k_{RBF} (r | \lambda) d \lambda \propto (1+ \frac{r^2}{2 \alpha \beta^{-1}} ) ^{- \alpha}$$

において、$\alpha=1$ かつ $2 \beta^{-1}= l^2$ としたものです。このことから、Cauchy カーネルを用いることは RBF カーネルの infine mixture を考えるのと等しいことがわかります。

推論モデル

上述した生成モデルにおける潜在変数 $\mathbf{z} _{1:T}$ の真の事後分布を求めることは困難であるため、変分推論により近似事後分布を求めることを考えます。ここで、表現能力を担保しつつ効率的に変分事後分布を求めるため、償却推論と構造化変分推論を用います。償却推論は、（データ点ごとに変分パラメータを設定するのではなく）VAE のエンコーダーのパラメータを変分パラメータとすることにより行います。構造化変分推論は、近似事後分布もガウス過程となるように設計することにより行います。

潜在変数 $\mathbf{Z} \in\mathbb{R}^{T \times k}$の各次元 $j$ について、事後分布 $p( \mathbf{z} _{1:T,j} | \mathbf{x} _{1:T} )$ を近似することを考えます。近似事後分布は多変量ガウス分布として設計します。

$$q( \mathbf{z} _{1:T,j} | \mathbf{x} _{1:T} ) = \mathcal{N}( \mathbf{m} _j, \mathbf{\Lambda} _j ^{-1} )$$

次元ごとに変分事後分布を設計することにより、潜在変数の各次元の独立性を仮定し計算の効率化を図りつつ、時間方向の相関関係を捉えることが可能です。

ここでは更なる計算の効率化のため、近似事後分布の精度行列 $\mathbf{\Lambda} _j$ を二重対角行列の積としてパラメトライズします。つまり

$$\mathbf{\Lambda} _j := \mathbf{B} _j ^{\top} \mathbf{B} _j \ , \text{with} \ \lbrace \mathbf{B} _j \rbrace _{t t^{'}} = \begin{cases} b _{t t^{'} } ^j & \text{if} \ t ^{'} \in \lbrace t, t+1 \rbrace \\\ 0 & \text{otherwise} \end{cases}$$

とします。このとき、精度行列 $\mathbf{\Lambda} _j$ は正定値対称な三重対角行列となります。精度行列は疎行列ですが、分散共分散行列は密行列となるため、全時点間の依存関係を反映できるのがポイントです。

近似事後分布のパラメータ $\mathbf{m}$ 及び $\mathbf{B}$ は、VAE のエンコーダーの出力として求めます（償却推論）。エンコーダーのパラメータを $\mathbf{\psi}$ とすれば $(\mathbf{m}, \mathbf{B}) = h _{\psi} (\mathbf{x} _{1:T} ^o )$ です。

モデルの学習

モデルの学習は、観測データの対数尤度の変分下限（evidence lower bound; ELBO）を、エンコーダー（推論モデル）とデコーダー（生成モデル）のパラメータ $\psi, \theta$ について最大化することにより行います。変分事後分布を $q _{\psi} (\cdot)$ と表すとすると、ELBO は次式のように求めることができます。

$$\begin{aligned} \log p(\mathbf{x} _{1:T} ^o) &= \log \int p _{\theta} (\mathbf{x} _{1:T} ^o, \mathbf{z} _{1:T} ) \ d \mathbf{z} _{1:T} \\\ &=\log \int q _{\psi} (\mathbf{z} _{1:T} | \mathbf{x} _{1:T} ^o) \ \frac{p _{\theta} (\mathbf{x} _{1:T} ^o, \mathbf{z} _{1:T} ) }{q _{\psi} (\mathbf{z} _{1:T} | \mathbf{x} _{1:T} ^o)} d \mathbf{z} _{1:T} \\\ & \geq \int q _{\psi} (\mathbf{z} _{1:T} | \mathbf{x} _{1:T} ^o) \ \log \frac{p _{\theta} (\mathbf{x} _{1:T} ^o, \mathbf{z} _{1:T} ) }{q _{\psi} (\mathbf{z} _{1:T} | \mathbf{x} _{1:T} ^o)} d \mathbf{z} _{1:T} \\\ & = \int q _{\psi} (\mathbf{z} _{1:T} | \mathbf{x} _{1:T} ^o) \ \log \frac{p _{\theta} (\mathbf{x} _{1:T} ^o| \mathbf{z} _{1:T} ) p(\mathbf{z} _{1:T} ) }{q _{\psi} (\mathbf{z} _{1:T} | \mathbf{x} _{1:T} ^o)} d \mathbf{z} _{1:T} \\\ & = \int \prod _{t=1}^T q _{\psi} (\mathbf{z} _{t} | \mathbf{x} _{1:T} ^o) \ \sum _{t=1} ^{T} \log p _{\theta} (\mathbf{x} _{t} ^o| \mathbf{z} _{t} ) \ d \mathbf{z} _{1:T}\ - \ \int q _{\psi} (\mathbf{z} _{1:T} | \mathbf{x} _{1:T} ^o) \ \log \frac{ q _{\psi} (\mathbf{z} _{1:T} | \mathbf{x} _{1:T} ^o) }{ p(\mathbf{z} _{1:T} )} d \mathbf{z} _{1:T} \\\ & = \sum _{t=1} ^T \mathbb{E} _{q _{\psi} (\mathbf{z} _{t} | \mathbf{x} _{1:T} ^o) } [ \log p _{\theta} (\mathbf{x} _{t} ^o| \mathbf{z} _{t} ) ] - D _{KL} [ q _{\psi} (\mathbf{z} _{1:T} | \mathbf{x} _{1:T} ^o) || p(\mathbf{z} _{1:T} ) ] \end{aligned}$$

三行目の変換では Jensen の不等式を用いました。なお、$\text{ELBO}$ の評価は観測されたデータ点についてのみ行います。また、推論時は欠損値にゼロを代入して学習を行います。さらに、データ欠損に伴う尤度項（第一項）と KL 項（第二項）のインバランスを代償するため、データ欠損率に応じ設定するハイパーパラメータ $\beta$ で KL 項をスケーリングすることが提案されています。

実験結果

GP-VAE の性能評価は、Healing MNIST・SPRITES・2012 Physionet Challange の３種類のデータで行っています。比較のベースラインとして挙げているのは以下です。

• Forward imputation：欠損時点以前で最後に観測された値で補間する。
• Mean imputation：全時刻における観測値の平均で補間する。
• VAE：潜在空間における時点間の関係性を考慮していない（事前分布に isotropic Gaussian を、変分事後分布に factorized Gaussian）。また、欠損値 (0) も観測値と区別せずに尤度計算を行う。
• HI-VAE：潜在空間における時点間の関係性を考慮していない（事前分布に isotropic Gaussian を、変分事後分布に factorized Gaussian）。欠損値 (0) はマスクし、観測点においてのみ尤度計算を行う。
• GRUI-GAN, BRITS：多変量時系列データ補間の SoTA モデルで、RNN を用いている。

まず、時系列の画像データに対する結果です。Healing MNIST は、時系列で MNIST 数字画像がランダムに回転するようなデータセットとなっています。SPRITES は、キャラクターが時系列にアクションをとるような画像が入ったデータセットとなっています。これら画像に対し、ランダムに 60%のピクセルを欠損させた上で、欠損値を正解と見なしてモデルの性能を評価しています。また Healing MNIST に対しては、補間した画像を入力とする数字の線形分類器を適用した際の分類精度も評価指標として用いています。

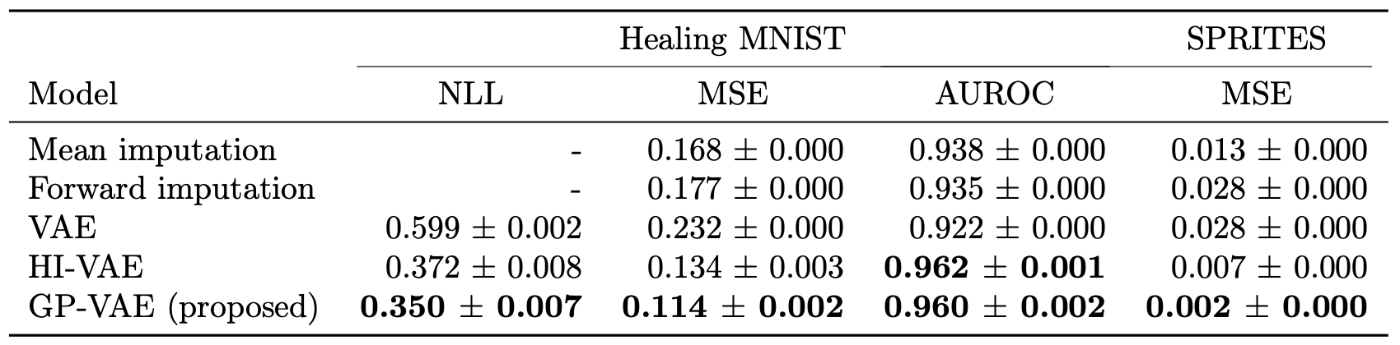
Healing MNIST ・SPRITES データに対する性能評価（出典：GP-VAE 論文 Table 1)

いずれの指標においても、GP-VAE がベースライン手法と比較して高い性能を発揮していることがわかります。以下は、各手法により補間を行った画像の一例です。

Healing MNIST ・SPRITES データの補間例（出典 GP-VAE 論文 Figure 2)

VAE や HI-VAE では潜在空間における時点間の相関関係をモデリングしていないため、同一時系列内での再構成結果に一貫性がなくなってしまっています（時点間で数字が異なる、キャラクターの色合いが異なるなど）。これに対し、時点間の相関関係をモデリングした GP-VAE では同一時系列内での再構成結果に一貫性が認められます。時系列モデリングの有用性を示唆する結果です。

次に、時系列の医療データ (2012 Physionet Challange) に対する結果です。こちらのデータは 12,000 人の ICU 入院患者につき、35 の項目を 48 時間にわたって 1 時間ごとに計測したものとなっています。前述した画像データと異なり、本データには正解が存在しない点が性能評価を難しくしています。人工的に欠損値を導入し正解を作ることも考えられますが、(1) すでに観測の 80%程度が欠損しておりデータがスパースになりすぎること、(2) 欠損の仕方がランダムではないこと、の二点から望ましくないと論じています。そこで本論文では補間した値に基づいて患者の予後予測を行い、予後予測の性能 (AUROC) に基づいてモデルの性能評価を行っています。予後予測には単純なロジスティック回帰を用いています。

予後予測の結果を示したのが Table 3 です。AUROC でベースライン手法を上回り、SoTA 手法である BRITS と比肩する性能を示していることがわかります。

Physionet データに対する性能評価（出典：GP-VAE 論文 Table 3)

実際に、3 つの変数に対する補間結果を示したのが Figure 3 です。緑色の点は観測された値を示しています。GP-VAE の補間結果は観測を説明しつつ、かつ時点間で滑らかに推定を行えていることがわかります。また、GP-VAE では推定の不確実性を求めることが可能なのもポイントです。不確実性の定量は、変分事後分布からサンプリングを行うことにより行っています。

Physionet データに対する補間例（出典：GP-VAE 論文 Figure 3）

一方で、例えば右の図のように、観測がスパースな時点で予測を大きく外している点は気になります。予測の不確実性も観測点に対応して計算できているわけではありません。このあたりの限界点は、潜在変数モデルを用いること・償却推論を用いることとトレードオフの関係にあるように思われます。

まとめ

本記事では、欠損値を含む多変量時系列データを対象とし、欠損値補間を行うための手法 GP-VAE の解説を行いました。

GP-VAE のモデリングのチョイスは、基本的には欠損値補間に適したものとなっており、時系列予測など別のタスクには向かないと考えます。というのも、近似事後分布推論の際に全時刻のデータへの依存を仮定しているからです。ただし、最終観測点に直近の時刻点という限定つきであれば時系列予測も部分的には可能ではあります。しかし、一般的な時系列予測は今回のままの構造では難しく、自己回帰的なモデリングを推論モデル・生成モデルに適用するなど行う必要がありそうです。一方で、VAE と確率モデルを組み合わせて得られる「チャネル（特徴量）方向・時間方向の相関を考慮できる」という性質は時系列の他の問題を解く上でも有用なので、モデリング次第では様々なシチュエーションに対応できるポテンシャルはあると考えられます。

潜在空間におけるガウス過程モデリングは VAE 拡張の有益な方向性の一つであり、時系列に特化したモデルとして本手法も一定の評価を受けています。次回は、時系列でないデータに対するガウス過程モデリングを行った論文を紹介したいと思います。