Zenn
🔖

巡回セールスマンゲームとシャープレイ値を近似するアルゴリズム (データ構造とアルゴリズム Advent Calendar 2021)

2021/12/10に公開
データ構造
アルゴリズム
数理最適化
tech

この記事は「データ構造とアルゴリズム Advent Calendar 2021」の10日目の記事として書きました．最近いろんな論文で「シャープレイ値」[1]を計算，もしくはその考え方を用いる手法を見るので，名前ぐらいは聞いたことがあるかもしれません．本記事では巡回セールスマンゲームとそのシャープレイ値を近似する簡単なアルゴリズムについて説明します．関連情報については，末尾の関連文献・URLを見て頂ければと思います．

例と定義と計算例

まずは例題から見ます．

例題 (4. 例1より)

シャープレイ値は，以下のように複数人のエージェントが便益を分配する状況において計算されることがある値です．

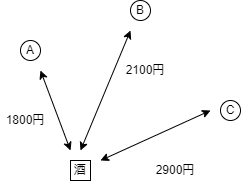
同じ方向に家のある A, B, C の3人が居酒屋からタクシーに相乗りして帰宅し，最後に下車した人が料金を支払い，翌日に皆で料金を精算することにした．その居酒屋からそれぞれの家にタクシーで直接帰宅した場合，Aの家まで1,800円，Bの家まで2,100円，Cの家まで2,900円の料金がかかる．またAの家からBの家までは1,800 円，Cの家までは2,000 円であり，BとCの家の間は2,300 円の料金が必要となる．最も安くなるルートで 3 人の家を回るとき，それぞれ，いくらずつタクシー料金を負担すればよいだろうか．

ここで3人が協力することにどういう旨味があるか？ということですが，もちろんバラバラにタクシーに乗るよりも少しでも安くしたいよね，という話があります．またタクシーが3往復する（もしくは3台のタクシーを呼ぶ）よりも社会的に良さそうな気持ちがしてきますね (e.g., SDGs)．

3人が別々に移動 3人がA\to B\to Cで移動
合計6800円 合計5900円
図1 図2

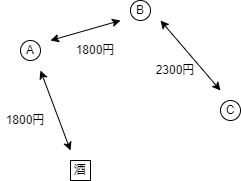ここで上の例1.に従って，2つ図を作りました．ABCが個別にタクシーを利用すると6800円 (Aは1800円，Bは2100円，Cは2900円) 必要でしたが，A\to B\to Cのタクシーを3人で割り勘すると合計5900円となり，900円節約できて嬉しい気持ちになります．今は3人を回る順番を A\to B\to Cとしましたが，3人のお家を巡回する方法は3!=6通り存在するので，それらを平均した上で計算した方が良いよね～という気持ちになります（現実ではならない場合もある気もしますが，全員が協力してくれるとしましょう）．

定義

上記の例に従って，そもそもシャープレイ値を定義しておきます．詳しい議論やシャープレイ値の性質などについては，協力ゲーム理論の本か論文を読んでください．

  • 特性関数形の協力ゲーム (N, v), v:2^N\to\mathbb{R}, v(\emptyset)=0が与えられたとき，プレイヤーiのシャープレイ値 \phi_i は以下の形で定義される量です:
\phi_i := \sum_{S\subseteq N\setminus\{i\}} \frac{|S|!(|N|-|S|-1)!}{|N|!} \left( v(S\cup\{i\}) - v(S)\right)

計算例

先の挙げた例を考えます．まずはお金の話を特性関数形の協力ゲームとして表現するために，v(S), S\subseteq Nとして，Sが全員個別にタクシーを利用して帰宅する場合と比較して，Sが協力することで節約できる料金として計算します．例えば上の例では，v(123)=9です (単位は[百円]とします，数字の文字列123は\{1,2,3\}を怠けて書いています)．

似たような形で計算すると，空集合を除いた2^n-1=7個のSについて以下のように特性関数を定義できます．

集合 1 2 3 12 13 23 123
特性関数値 0 0 0 3 9 6 9

このようなvが所与のとき，\phi_1を計算してみます．

  • S\subseteq N\setminus\{1\}=\{2,3\}を考えるので，S=\emptyset, \{2\}, \{3\}, \{2,3\}です．
  • |S|=0のとき，係数は\frac{0!(3-0-1)!}{3!}=\frac{2}{6}=\frac{1}{3}，値はv(1)-v(\emptyset)=v(1)=0です．
  • |S|=1のとき，係数は\frac{1!(3-1-1)!}{3!}=\frac{1}{6}，値は
    • v(12)-v(2)の場合，v(12)-v(2)=v(12)=3です
    • v(13)-v(3)の場合，v(13)-v(3)=v(13)=9です
  • |S|=2のとき，係数は\frac{2!(3-2-1)!}{3!}=\frac{2}{6}=\frac{1}{3}，値はv(123)-v(23)=3です．
  • これを全部合わせると，\phi_1=\frac{1}{6}\times 3 + \frac{1}{6}\times 9 + \frac{1}{3} \times 3 = 3です．
  • 似たように計算すると \phi_2=1.5, \phi_3=4.5 になります．

もちろんクソ雑に実装するとまったく効率的ではありませんが…．

kuso.jl
using Combinatorics

# 特性関数の値
N = [1, 2, 3]
vs = [0, 0, 0, 0, 3, 9, 6, 9]
dictv = Dict()
for (k, S) in enumerate(powerset(N))
    dictv[Set(S)] = vs[k]
end

# naive計算
function naive_compute_shapley(N, dictv, i)
    Ni = [j for j in N if j != i]
    fN = factorial(length(N))
    value = 0.0
    for S in powerset(Ni)
        S = Set(S)
        Si = union(S, i)
        comp = factorial(length(S)) * factorial(length(N) - length(S) - 1) / fN
        value += comp * (dictv[Si] - dictv[S])
    end
    value
end

ϕ = [naive_compute_shapley(N, dictv, k) for k in 1:length(N)]
println(ϕ) # => [3.0, 1.5, 4.5]

巡回セールスマンゲームとシャープレイ値の計算

前提

これまでタクシーの料金のようにお金の話を考えてきましたが，もう少し抽象的に考え，巡回セールスマン問題を考えましょう．巡回セールスマン問題は，しばしば人間には解けない問題の例として使われているのでちょうど良いです (怪しい日本語です．詳しくは参考文献5.を読んでください)．適当に書くと，n個ぐらい訪問しないといけない地点があり，地点間の移動コストがC_{i,j}\in\mathbb{R}, i, j\in[n]で与えられているときに，移動コストが最小になる順回路を求めるような問題でした．

この記事では，集合Sに対する値v(S)として，集合Sのみを訪問する巡回セールスマン問題の最適解の移動コストとして設定した場合に，シャープレイ値を求めたい気持ちの問題を考えます．上のタクシーのように，このような問題設定を巡回セールスマンゲーム (Traveling Salesman/Salesperson Game) と呼びます．論文などでは真面目な定義が著者ごとにいろいろと出てきて混乱するのですが，この記事ではこの設定です．

この記事の目的は，もし巡回セールスマンゲームのシャープレイ値をどうしても計算したくなった場合に，上のnaive_compute_shapleyよりも多少はマシな計算 (ただし厳密ではない) を実装したい人が読むと良い情報をまとめることです．具体的には比較的簡単に実装できる ApproShapley と，1次の近似アルゴリズムである Approx-O(1) を説明して実装します．また私が理解できなかった2次の近似アルゴリズムであるApprox-O(2) と，2021年現在もっとも良いと言われている SHAPO について情報の断片をまとめておきます．

ApproShapley

シャープレイ値の計算式 (上の例) は，あるプレイヤーiが参加したときの増分 v(S\cup\{i\}) - v(S) を，可能なすべてのS\subseteq N\setminus\{i\}で計算して平均したような値になっていました．ここで一つ考えられるアプローチとして，適当な順列 \pi を取ってきて，iを訪問する前と後の増分を計算して適当に平均する (e.g., モンテカルロ法的なもの) アプローチがあります．この手法を ApproShapley と呼びます．原著と名目はこちらの論文らしいです．

  • I. Mann and L. S. Shapley, Values for large games, IV: Evaluating the electoral college by Monte Carlo techniques, Technical report, RAND Corporation, 1962
  • J. Castro, D. Gomez, and J. Tejada, Polynomial calculation of the Shapley value based on sampling. Computers & Operations Research, 36, 1726–1730, 2009

もう少し式で説明します．n地点の訪問順をすべて収めた順列の集合を \mathcal{S}_n とし，1つ取ってきたランダムな順列 \pi\in\mathcal{S}_n とします．ここで新しく \pi_i を定義します．これは順列 \pi の中で，要素 i に先行する地点の集合です．ApproxShapley ではこのような\piを適当にm個ぐらい取ってきて

\hat{\phi}_i := \frac{1}{m} \sum_{\pi\in\mathcal{S}_n} \left( c(\pi_i\cup\{i\}) - c(\pi_i)\right)

と計算します．個別のc(\cdot)評価はコンコルドを呼べば良いので (!?) これで終了です．

Approx-O(1), Approx-O(2)

Approx-O(1)とApprox-O(2)は，以下の論文で提案された2020年頃に一番良いと呼ばれていたらしい (?) アルゴリズムです．

  • D.C. Popescu and P.Kilby, Approximation of the Shapley value for the Euclidean travelling salesman game, Annals of Operations Research, 289:341-362, 2020

Approx-O(1)については式を読めば簡単に実装できますが，Approx-O(2)については説明がまったく分からず理解出来ませんでした．

基本的なアイデアは，ユークリッドTSPを考えるとき，特殊なケースの計算を閉じた式で書き表し，それを一般の場合のTSP/TSGに対しても拡張して利用するというのがアイデアです．Approx-O(1)は直線上のTSGから，Approx-O(2)は平面のTSG (特に三角に注目) から着想を得た近似手法です．以下にApprox-O(1)を説明し，計算方法を示します．

考え方1: 直線上のTSG

直線上の問題でTSGを考えます．

直線

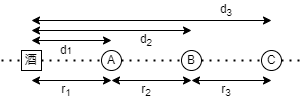
図の通りすべての訪問地点は直線上に位置しており

  • r_1 = d_1
  • r_j=d_j-d_{j-1} (2\leq j\leq n)

とします．このような場合に効率的に計算できるでしょうか? 実はできます (!?)．実はこのときのシャープレイ値は簡単な式として

\phi_k^\star := \sum_{j=1}^k \frac{2r_j}{n-j+1}

で計算できることが知られています．本当にこんな式になるのか?となりますが，これまで上で手計算してきたシャープレイ値の計算を線上のケースに真面目にやると，この式が得られます．今，数直線上の原点から正の方向にA(1), B(2), C(3)と並んでいるとすると，定義によると，例えば\phi_1について

  • \pi=123のとき，c(1)-c(\emptyset)=2d_1
  • \pi=132のとき，c(1)-c(\emptyset)=2d_1
  • \pi=213のとき，c(12)-c(2)=0
  • \pi=231のとき，c(123)-c(23)=0
  • \pi=312のとき，c(13)-c(3)=0
  • \pi=321のとき，c(123)-c(23)=0

を計算し，最終的には\frac{4}{3!}d_1=\frac{2}{3}d_1となります．ここで\phi^\star_kの式に対して，k=1とr_1=d_1を使うとすぐに\phi_1^\star := \frac{2}{3}d_1となります．似たように定義式の計算と，\phi^\star_kの計算が線上の場合に一致することが分かります．例えば\phi_2について考えると，上と同じように表を用いて計算すると\phi_2=d_2-\frac{1}{3}d_1となりますが，閉じた式から計算すると

\phi^\star_2=\frac{2}{n}r_1 + \frac{2}{n-1}r_2 = \frac{2}{3}r_1 + r_2 = \frac{2}{3}d_1 + d_2 - d_1 = d_2 - \frac{1}{3}d_1

となって一致します．

さて論文ではこの式を一般化するために，次のような量を定義します．

\mathrm{SC}(x_1,\dots,x_k) := \sum_{i=1}^k \frac{y_i}{i (i + 1)}

ただし [y_1,\dots,y_k]とは，[x_1,\dots,x_k]という入力の値を降順でソートしたものです．この量を利用すると一般的な近似式として，|N|=nについて

\phi^\star_n := 2d_n - \mathrm{SC}(2d_1,\dots,2d_{n-1})

また途中のkについて，k以降の\mathrm{SC}(\cdot)部分をすべて2d_kで置き換え

\phi^\star_k := 2d_k - \mathrm{SC}(2d_1,\dots,2d_{k-1},2d_{k},2d_k,\dots,2d_k)

の式で計算することができます．

考え方2: 三角形の場合

次に三角形のTSGを考えます．

三角形

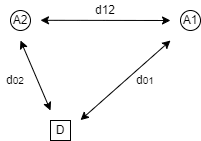
真面目にシャープレイ値を計算すると，次のことが分かります．

  • \phi_1 = \frac{1}{2}(3d_{01} - d_{02} + d_{12}) = 2d_{01} - \frac{1}{2}(d_{01}+d_{02}-d_{12})
  • \phi_2 = 2d_{02} - \frac{1}{2}(d_{01} + d_{02} - d_{12})

ここで便宜上

s_{ij} := d_{0i} + d_{0j} - d_{ij}

と定義します．0は出発地点のDのことです．これは三角形のうち，直接両者にタクシーで行くコストから間を結ぶコストを引いたもので，これを shared distance と呼びます．この定義を用いると，（天下り的ですが）計算は以下の形で表現できます．

  • \phi_1 = s_{11} - \frac{1}{2}s_{12} = s_{11} - \mathrm{SC}(s_{12})

計算方法

これまで天下り式で与えてきた計算式に基づいて，以下の形で近似計算を行うアルゴリズムがApprox-O(1)です．

\tilde{\phi}_k = s_{kk} - \mathrm{SC}(s_{1,k}, s_{2,k}, \dots, s_{k-1,k}, s_{k+1,k}, \dots, s_{n,k})

Approx-O(2)について

三角形の計算を抽象化し，誤差はありながらも，一般の計算式に転用したアルゴリズムがApprox-O(1)でした．この流れに乗っていくと，四角形，五角形，…を考えていって近似式が作れそうな気配を感じます (私は感じません)．実際，Approx-O(2)は四角形のTSGから出発した近似計算式であり，より性能が高くなると言われています．

SHAPO

最後に2021年現在，比較的優れているとされているSHAPOです．以下の論文が出典です．

  • C. Levinger, N. Hazon, and A. Azaria, Computing the Shapley Value for Ride-Sharing and Routing Games, AAMAS2020
  • C. Levinger, N. Hazon, and A. Azaria, Efficient computation and estimation of the shapley value for traveling salesman games, IEEE Access 9:129119-129129, 2021

SHAPOですが，実はApproShapleyと近い気持ちを持っています．ApproShapleyの計算式をより高精度・高速に場合分けして計算したものがSHAPOのアプローチです．アルゴリズムを論文からパクってきて貼ります (雑)．

SHAPO

なぜこのアルゴリズムを紹介しないのかというと，そこまで真面目に理解できなかったことと，実装しても精度がそこまで出ずに沼ったからです．論文の図から読むと，SHAPOはstate-of-the-artな性能を示していますが，分かりませんでした (投げやり)．

厳密計算 vs ApproShapley vs Approx-O(1)

最後に3つの手法を実装して比較してみます．上に述べたとおり本当は関数 c(\cdot) の計算は真面目なTSPソルバーを用いるべきだったのですが，面倒だったので小さい例だけで計算して，c(\cdot)は力技で計算することにしました．

レポジトリです．実装はゴミなので使わないでください．

https://github.com/cocomoff/SmallTSG

計算結果 (時間) と厳密計算との比較です．なるほどですね～（雑）．

時間 数値比較

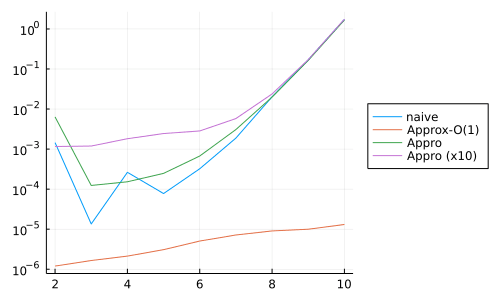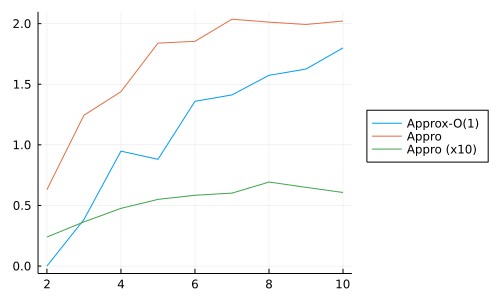Approは中身でTSPの評価値c(S)を全部計算しているのでnaiveと一緒になってしまいます (ダメです)．ちゃんとconcordeを呼びましょう．ApproとAppro(x10)はランダムに作成する\pi\in\mathcal{S}_nの個数が10倍になっているので，精度が上がります．あとグラフとかは適当に書いたのでダメです．Approx-O(1)かApprox-O(2)，またはSHAPOを使いましょう．

まとめ

この記事では，明日業務で「巡回セールスマンゲームのシャープレイ値を計算して！」と言われる場合に備えて，いくつかの近似アルゴリズムを紹介しました．

参考文献など

  1. Wikipedia シャープレイ値
  2. Interpretable Machine Learning §5.9 シャープレイ値
  3. 協力ゲーム理論のシャープレイ値に基づき機械学習モデルの予測を解釈するKernel SHAPの理論と実装のまとめ
  4. 岸本信, 協力ゲーム理論入門, オペレーションズリサーチ 2015年6月号
  5. 「量子」と組合せ最適化に関する怪しい言説 ―とある研究者の小言―
脚注

  1. Wikipediaの定義なら参考文献の1.を，機械学習への応用については2.3.を，一般的な協力ゲーム理論の枠組みにおけるシャープレイ値に興味がある場合は4.などを見てください ↩︎

Discussion