カープーリング問題を学んできた (数理最適化 Advent Calendar 2024)
はじめに
Twitter芸人名@cocomoffです。1-1.5年に1回ぐらい、数理最適化っぽい小ネタをブログに書いています。
- 小ネタ集
数理最適化の業務から首になり最近は探索ばかりしているのですが、この前シンポジウムでタイトルにある「カープーリング問題」を勉強してきたので今年も書くことにしました。ChatGPTに頼りつつ、やっていこうと思います(Google OR-Toolsを使うのが3年ぶりぐらいだった…)。
CPP (Car Pooling Problem) | カープーリング問題
基本的な考え方
カープーリングの基本アイデアですが
というパワー系のものです。
というのも、ほとんどの場合通勤車両は運転手しか乗っておらず空気を運んでいます。空いてるところに他の乗客を詰め込めば、みんなハッピーになるだろうと予測されます(?)。道路は容量が限られているので、通行車両数を減らすことで様々な効果があります。最近のITS系論文などを読むと、だいたい背景のところに「交通渋滞の悪影響は〜」みたいなことが書いてありますね。怪しいですね。
こういうものを見てもらうと雰囲気はわかる気がします。
問題の立ち位置
論文や解説を読むと「DARP (Dial-a-ride problem)」の特殊ケースと書いてあることがあります。DARPはVRPPDTW (VRP + Pickup and Delivery + Time Window)の一般化と書いてあります。VRP (Vehicle Routing Problem) はTSPの一般化問題の一種です。
これで雰囲気がわかりましたね。
こういうイメージです (参考文献その3 p5より引用)。

通勤時に使い、相乗りによって効率化を目指すことを考えると
- 目的地を全員共通のdepot(□)にする
- 車を出す人 (servers) と同乗する人 (clients) に分かれる
- 車を出す人は(乗れる分だけ)、同乗する人を選んで乗せてから会社に向かうことができる
- 運が悪い人は乗れない
というような性質を持つDARPがcar poolingと考えられます。
定式化
参考文献その2によれば、いくつかの定式化アプローチがあります(DARPの元になるVRPに対しても似たようなアプローチがあります)。具体的には「3-index法」と「集合分割法」が紹介されています。
この記事では一番直感的であり、多くのインターネット記事でもTSP/VRP向けの定式化で使われている3-index法を見てみます。
問題と解の表現
有向グラフ
- 頂点の集合
V=\{0,1,\dots, n\}=\{0\}\cup V' -
0 -
V'=\{1,\dots,n\} = V_s\cup V_c, V_s:=\{1,\dots,n_s\}, V_c:=\{n_s+1,\dots,n\} -
V_s n_s -
V_c n-n_s
-
-
- 有効辺について
- 頂点
i\in V \Gamma_i := \{j\in V \mid (i, j) \in A\} \Gamma_i^{-1} = \{i\in V \mid (i, j) \in A\} - 各辺
(i,j)\in A d_{ij} t_{ij}
- 頂点
- 従業員
i\in V' e_i l_i - 👀 待ち続けるわけにはいかないみたいな従業員を表現します
- ドライバー
k\in V_s Q_k T_k~(t_{k0}\leq T_k\leq l_k - e_k) - 👀 長く運転したくない&車の乗車上限がある
- 解は単純パス
P=(i_1,i_2,\dots,i_m,i_{m+1}) -
i_1\in V_s -
i_2,\dots,i_m\subseteq V_c -
i_{m+1}=0
-
- 許容解は以下の要件を満たします
- (1) 容量制約を満たす (
P Q_{i_1} - (2) 全移動時間は
T_{i_1} - (3) 出発/到着時間制約を満たす
- ※式を書くのが大変なので省略。移動したときに
e_i, l_i
- ※式を書くのが大変なので省略。移動したときに
- (1) 容量制約を満たす (
雰囲気はこれでだいたいわかりました。
決定変数と目的関数
典型的な決定変数を準備します。
-
x_{ij}^k\in\{0,1\} (i,j) k 1 -
y_i\in\{0,1\} i\in V_c 1
目的関数として「距離」と「乗せなかった場合のペナルティ」を使います。
この式では、乗車させないペナルティでは、顧客
のようにすることもあります(参考文献その2 式(3))。いずれにしても何かしらのバランスが取られることになります。
制約
たぶんTSPTWやVRPTWを書いたことある人は見たことある式だと思うので、論文を読んでください(?)。
観察
GPT4oと対話しながら実例を作成しつつ、「式(3)-式(16)をGoogle OR-Toolsで実装してください」というプレイをしていました。得られたものを書いていきます。今回は議論をかなり簡単化するために時間制約は省いてしまいました(本当に拾いに行くだけ)。
実装トライアル (GPT4)
例はGPTが吐き出したものを微調整しました。グラフ
本当は辺集合
from ortools.linear_solver import pywraplp
import networkx as nx
import matplotlib.pyplot as plt
def solve_and_visualize_carpooling():
solver = pywraplp.Solver.CreateSolver('SCIP')
# Example data
depot = 0 # Depot
drivers = [1, 2] # Drivers
riders = [3, 4, 5] # Riders
nodes = [depot] + drivers + riders
# Cost matrix
cost = {
(1, 3): 4, (1, 4): 3, (1, 5): 5,
(2, 3): 2, (2, 4): 6, (2, 5): 2,
(1, 0): 5, (2, 0): 5,
(3, 0): 7, (4, 0): 8, (5, 0): 6,
(3, 4): 1, (3, 5): 1,
(4, 5): 1
}
# Graph
G = {
1: [3, 4, 5, 0],
2: [3, 4, 5, 0],
3: [4, 5, 0],
4: [3, 5, 0],
5: [3, 4, 0],
0: []
}
Ginv = {
1: [],
2: [],
3: [1, 2, 4, 5],
4: [1, 2, 3, 5],
5: [1, 2, 3, 4],
0: [3, 4, 5]
}
# Driver capacity
capacity = {1: 2, 2: 2}
# Penalty for unserved riders
penalty = {3: 10, 4: 15, 5: 10}
# Variables
x = {}
for i in nodes:
for j in nodes:
if i != j:
for k in drivers:
x[i, j, k] = solver.BoolVar(f'x[{i},{j},{k}]')
y = {i: solver.BoolVar(f'y[{i}]') for i in riders}
# Objective function
objective = solver.Objective()
for (i, j), c in cost.items():
for k in drivers:
if (i, j, k) in x:
objective.SetCoefficient(x[i, j, k], c)
for i in riders:
objective.SetCoefficient(y[i], penalty[i])
objective.SetMinimization()
# Constraints: Start & Goal
for k in drivers:
solver.Add(sum(x[k, j, k] for j in G[k] if j != k) == 1)
solver.Add(sum(x[j, depot, k] for j in Ginv[depot] if j != depot) == 1)
# Constraints: Flow conservation constraints
for k in drivers:
for i in riders:
solver.Add(sum(x[i, j, k] for j in G[i] if j != i) ==
sum(x[j, i, k] for j in Ginv[i] if j != i))
# Constraints: Rider service constraints
for i in riders:
solver.Add(sum(x[i, j, k] for j in nodes for k in drivers if i != j) + y[i] == 1)
# Constraints: Capacity constraints
for k in drivers:
solver.Add(sum(x[i, j, k] for i in riders for j in nodes if i != j) <= capacity[k])
# Solve
status = solver.Solve()
# Visualization
G = nx.DiGraph()
if status == pywraplp.Solver.OPTIMAL:
for (i, j, k), var in x.items():
if var.solution_value() > 0.5:
print(f"Driver {k} transports from {i} to {j}")
G.add_edge(i, j, label=f"Driver {k}")
for i, var in y.items():
if var.solution_value() > 0.5:
print(f"Rider {i} is not served (penalty applied).")
print("Minimum cost:", solver.Objective().Value())
# Draw graph
pos = nx.spring_layout(G)
nx.draw(G, pos, with_labels=True, node_size=500, node_color='lightblue', font_size=10, font_weight='bold')
edge_labels = nx.get_edge_attributes(G, 'label')
nx.draw_networkx_edge_labels(G, pos, edge_labels=edge_labels)
plt.title("Carpooling Optimization with Initial Positions")
plt.savefig("output.png", dpi=300, bbox_inches="tight")
plt.close()
else:
print("No optimal solution found.")
if __name__ == '__main__':
solve_and_visualize_carpooling()
計算例
このような解が得られました(それっぽいですが、嘘解法の解になってます、難しいですね)。

GPT4くんを信じていたら、こういうダメな解も出てきちゃいました。どこがいけなかったでしょうか?(ここからが大変…)。
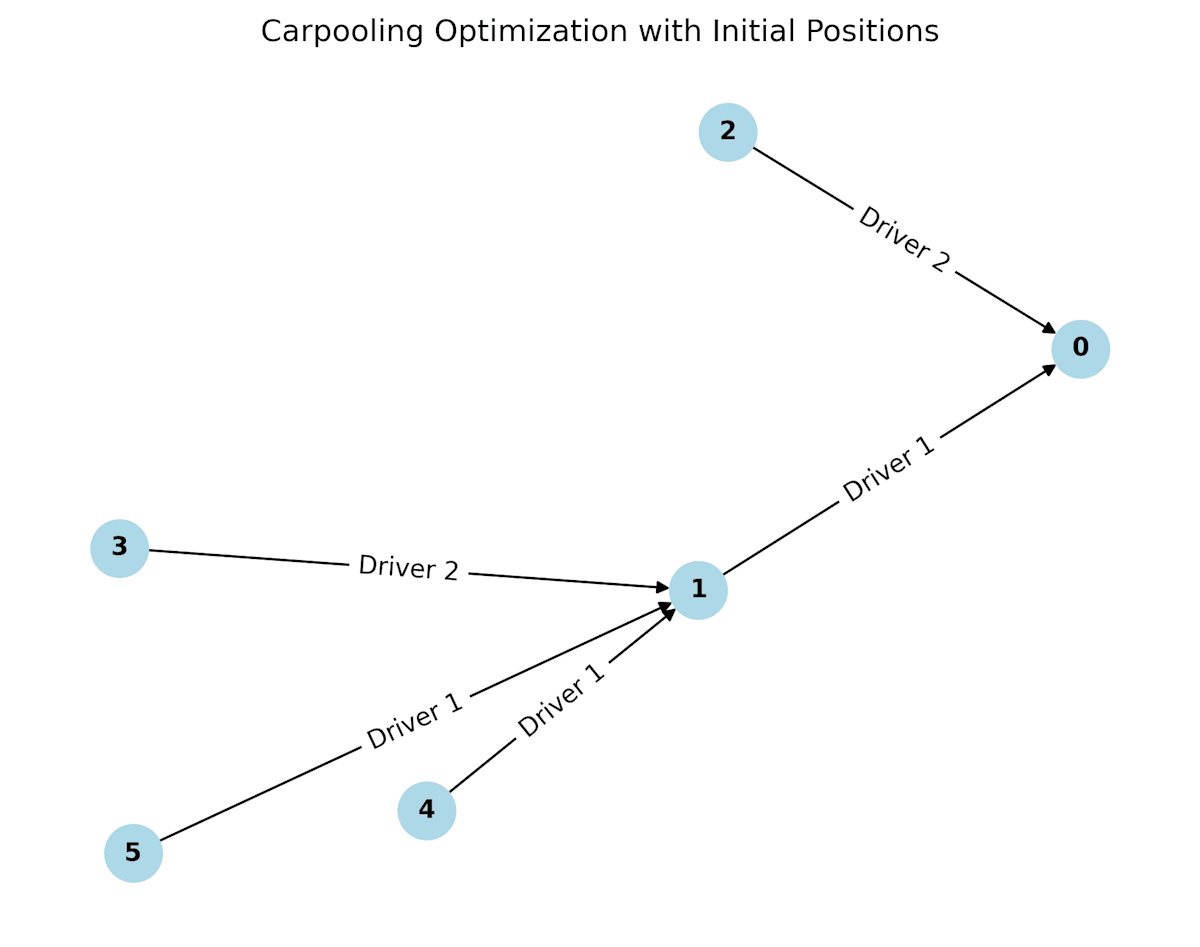
ここからGPT4の調教の旅に出ていたら帰ってこれなくなりました(1敗)。
まとめ
真面目な話を知りたい方は、まずこの記事より参考文献その1を読みましょう。またGPTくんは問題インスタンスをランダムに作ってくれる(一応)ので、そういう楽しさはある気がします。
また勉強して真面目に実装を改良したら記事を書きたいと思います。
余談です。最初は論文や参考文献を読み、それをGPT4oに丸投げしたら記事になるだろ!と思って突っ込んだのですが、流石に無理だったので書き直しました。
参考文献など
- 橋上, 繁野, 数理最適化を用いたサービス工学の事例―通勤カープールの実証実験―.
- Baldacci et al., An exact method for the car pooling problem based on lagrangean column generation, Operations Research, 2004.
- The dial a ride problem (DARP), https://rasmuspagh.net/courses/CAOS/DARP.pdf, CAOS, 2005.
Discussion