モジュラリティ最大化の計算を例に定式化の違いを見る (数理最適化 Advent Calendar 2022)

Twitter: @cocomoff / Zenn: @takilog です。本記事は 数理最適化 Advent Calendar 2022 の15日目の記事として書きました。今年、お仕事（研究）でいろんな最適化問題を見ていて、定式化のあーだこーだで悩むことが多かったので気分転換で書いている側面もあります。

はじめに

普段、職場のメンバと論文などを紹介しあう会を不定期にやっています。ある回でこの2本の論文を紹介しました。中身はこの記事には関係ないので一言コメントだけ付けておきますね（興味のある人は論文も見てみてください）。

• Gaurav Agarwal and David Kempe, Modularity-maximizing graph communities via mathematical programming, The European Physical Journal B 66, pp.409-418, 2008
  • （一言でいうと）LPやQP、階層的なアルゴリズムなどを通じてモジュラリティ最大化によるコミュニティ検知についてまとめられている論文です。
• Filipi N. Silva, Aiiad Albeshri, Vijey Thayananthan, Wadee Alhalabi, and Santo Fortunato, Robustness modularity in complex networks, Physical Review E 105, 054308, 2022
  • （一言でいうと）通常のモジュラリティはある程度意味のない構造でも数値が出ることがあるので、null modelを設定してランダム性に基づき、モジュラリティの計測にロバスト性を入れる手法についての話です。

ここで出てくるグラフのモジュラリティ (Modularity) はネットワーク解析でコミュニティ構造（頂点の分割のこと）を定量化したり議論するためによく使われる量です。式の真面目な解説はネット上の記事か、上の Wikipedia の記事などを参考にしてください。

簡単なイメージだけ考えると、ある2つの頂点 $u, v\in V$ について、「$u$ と $v$ が同じクラスタに属しているなら $1$ (または $0$)」のような最適化問題として書くことができるため、モジュラリティの話は数理最適化 Advent Calendar のスコープということですね（？）。

定式化の比較

上の論文を読んでいて、論文の定式化とUme本^[1]の定式化が異なっていたので、面白いなと思って比較してみることにしました。

論文の説明

論文の通り説明します（記号は適当に変えています）。

無向グラフ $G=(V, E)$ と頂点 $u, v\in V$ について、$m_{u, v} := A_{u,v} - \frac{d(u) d(v)}{2m}$ を定義しておきます。ただし $A$ は $G$ の隣接行列（対称）です。また $d(u)$ と, $d(v)$ は頂点 $u$ と $v$の次数です。ついでに $m=|E|$ です（そもそもグラフの話をするとき、暗黙的に $|V|=n, |E|=m$ と書くことが多いですね？）。

このとき、モジュラリティ最大化によるコミュニティ発見問題の目的関数と制約は以下の通りです。

• 目的関数

$$\max \frac{1}{2m} \sum_{u, v} m_{u, v} (1 - x_{u, v})$$

• 制約条件

$$x_{u,w} \leq x_{u,v} + x_{v,w}\hspace{1em}\text{for all }u, v, w$$

$$x_{u,v} \in \{0, 1\}\hspace{1em}\text{for all }u, v$$

• 変数の解釈: $x_{u, v} = 0$ は $u$ と $v$ が同じクラスタに属することを意味する

以上の設定の下で、制約は次のように解釈できます（読まなくていいです）。

解釈

• もし$u$と$w$が同じクラスタに属していないとします（左辺が1）。このとき、右辺は1以上にならなければならず、$u$と$w$とは別の頂点$v$を考え、どちらからが$1$になる、つまり「$x$と$u$が別のクラスタ」または「$u$と$w$は別のクラスタ」が必ず成り立たなければなりません（両方成り立ってもいい）。両方成り立つ場合、$x, v, w$は任意な3ペアについて成り立つので、それぞれ別のクラスタになります。片方だけが成り立つ場合には、$u, v, w$の3ペアが2クラスタに分かれる雰囲気になります。
• もし$u$を$w$は同じクラスタに属しているとします（左辺が0）。このとき、右辺は0以上にならなければなりません。すると右辺は、上の場合とことなり、両方0が許されます。両方0は、$u, v, w$が同一クラスタに属する状況です。それ以外の場合分け（上と同じ）も許可されます。何か少しゆるそうですね！。
• こんなのでうまく行くんですかね？不思議ですね〜（雑）。

Ume本の説明

この記事を読む人はおそらく本を所持していると思いますので（？？？）詳細は本を読んで頂くとして、このように分解された式で不等式制約を書いています。ついでに目的関数も$u < v$の関係を使って整理されています。書籍ではp.163あたりに書いてあります。

• 目的関数

$$\max \frac{1}{m} \sum_{u\in V} \sum_{v\in V, v > u} m_{u, v} x_{u, v} + \frac{1}{2m} \sum_{u\in V} m_{u, u}$$

• 制約条件

$$x_{u,v} + x_{v,w} - x_{u,w} \leq 1, \hspace{1em}u, v, w \in V, u < v < w$$

$$x_{u,v} - x_{v,w} + x_{u,w} \leq 1, \hspace{1em}u, v, w \in V, u < v < w$$

$$-x_{u,v} + x_{v,w} + x_{u,w} \leq 1, \hspace{1em}u, v, w \in V, u < v < w$$

$$x_{u, v} \in \{0, 1\}\hspace{1em}\text{for all }u, v\in V, u < v$$

• 変数の解釈: $x_{u, v} = 1$ は $u$ と $v$ が同じクラスタに属することを意味する

こちらの制約は次のように解釈できます（本のコピペです）。

解釈

• 制約1だけを考えます。これは「もし$u$と$v$が同じクラスタ」であり「$v$と$w$が同じクラスタ」であるとき、$u$と$v$も同じクラスタ」という推移律を表しています。式を見ると、$-x_{u,w}$ が効いてくるわけですね。
• 制約2と3も同じ考え方です。

実装・実行結果

これまでの説明を振り返ると、$0/1$ の解釈が反転したモデルが2つ知られていることが分かりました。2つモデルがあるので、実装して挙動を確認してみたくなります。早速実装してみると、雰囲気は以下に示すようなコードになります（真面目な実装ではないので使いまわしなどはしない方が良いです）。それぞれ $G$ がPythonのnetworkxの無向グラフとして入力されるとしています。

論文モデルの実装

式では for all しか書いていないところでこのような実装スタイルにしました（正しいかどうかは…？論文はこれだからダメです！）。

n = G.number_of_nodes()
m = G.number_of_edges()
nodes = list(G.nodes())

A = nx.adjacency_matrix(G).todense()
M = {(u, v): 0 for (u, v) in product(nodes, nodes)}
for i in nodes:
    for j in nodes:
        Aij = 1 if j in G[i] else 0
        M[i, j] = Aij - G.degree(i) * G.degree(j) / (2 * m)

# solve
model = P.LpProblem("max-modularity", sense=P.LpMaximize)
x = P.LpVariable.dicts("x", (nodes, nodes), 0, 1, cat="Integer")

model += P.lpSum(M[i, j] * (1 - x[i][j]) 
                 for (i, j) in product(nodes, nodes)) / (2 * m)
for (i, j, k) in product(nodes, nodes, nodes):
    if len(set({i, j, k})) == 3: # ここは適当です
        model += x[i][k] <= x[i][j] + x[j][k]

solver = P.SCIP(msg=0)
model.solve(solver)

Ume本モデルの実装

次はUme本の実装ですが、こちらは $u < v < w$ のように丁寧に条件が書かれているので、実装時もクリアです。

n = G.number_of_nodes()
m = G.number_of_edges()
A = nx.adjacency_matrix(G).todense()
M = {(u, v): 0 for (u, v) in product(range(n), range(n))}
for i in range(n):
    for j in range(n):
        Aij = 1 if j in G[i] else 0
        M[i, j] = Aij - G.degree(i) * G.degree(j) / (2 * m)

# solve
model = P.LpProblem("max-modularity", sense=P.LpMaximize)
x = P.LpVariable.dicts("x", (range(n), range(n)), 0, 1, "Integer")

obj1 = P.lpSum(M[i, j] * x[i][j]
               for i in range(n) for j in range(i + 1, n)) / m
obj2 = P.lpSum(M[i, i] * x[i][i] for i in range(n)) / (2 * m)
model += obj1 + obj2

# 後で考えたら (u, v, w) にしたほうが良かった…
for i in range(n):
    for j in range(i + 1, n):
        for k in range(j + 1, n):
            model +=  x[i][j] + x[j][k] - x[i][k] <= 1
            model +=  x[i][j] - x[j][k] + x[i][k] <= 1
            model += -x[i][j] + x[j][k] + x[i][k] <= 1

solver = P.SCIP(msg=0)
model.solve(solver)

あとは動かしてみるだけですね。

動作確認

上のコードを実際に動かします。

0-1の整数計画問題のため、小さめのグラフで動作を確認することにします。0-1の整数計画問題を連続緩和して丸めながら解く方法なども論文に紹介されていますので、興味がある方はそちらも確認してみてください。実際に実装してみると、そこそこの近似解が出ました。

karate club

有名なグラフデータです。

コミュニティ検知の手法自体は、networkxに実装されているヒューリスティクス や貪欲法が使えるので、それらも適用した上で結果を出力してみました。ネットワークの可視化が適当でpulpの解だけ見た目が変わってしまっています。

良さそうな感じですね。

貪欲法	もっと賢いやつ (Louvain)	pulpの解

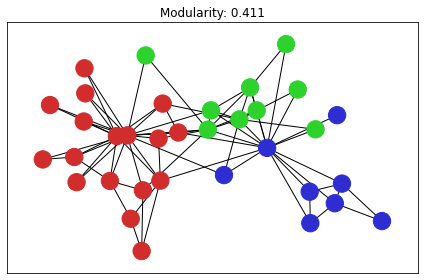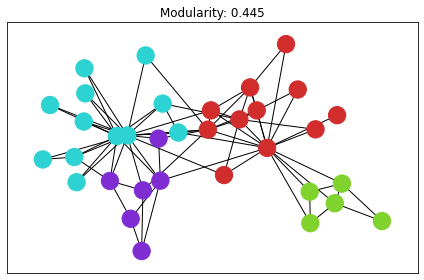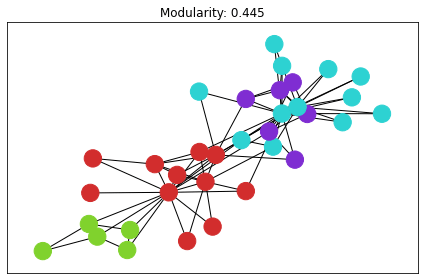random geometric graph

ランダム幾何グラフでも動かしてみます。サイズ$N$のランダム幾何グラフを以下のコードで生成して、計算に使っています。

G = nx.random_geometric_graph(N, 0.55)

サイズ$N$を適当に変えながら計算時間を確認してみます。下の図は論文のモデル (Paper) とUme本のモデル (Umepon-book) の計算時間の比較結果のプロットです（plotするのを忘れましたが、モジュラリティの値はこの場合はどちらも同じでした）。途中で計算時間がサチってきたのは、ランダム幾何グラフのせいだと思います（特に検証してないですが…）。

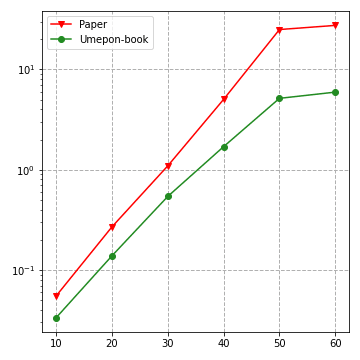
結果を見ると、安定してUmepon-bookのモデルの方が高速に計算できた様子です。制約が良かったみたいですね。このように同じ問題の実装でも制約をうまく設定して実行可能領域などをいい感じに表現できていると、結果に響いてくるわけですね。しっかり制約を準備しましょう！（雑）。

まとめ

モジュラリティ最大化ぐらいメジャーな問題だと、良い多面体を表現する不等式を世の中の人が考えていると思います。論文を探すと見つかる可能性が高いでしょうか。

一方で、企業の謎にカスタマイズされたものは望み薄でしょうか。原理検証で汎用の数理最適化ソルバーを使うことは多いと思うので、そのまま力づくでソルバーに投げてポイっとやってしまうしかないですね。難しいですね〜（雑）。これからもいろいろと頭を悩ませながら仕事することになりそうです。

来年こそは真面目な記事を書くつもりでいます（フラグ）。

脚注

1. 梅谷先生の最適化本のことです（しっかり学ぶ数理最適化）。