Juliaで資産運用のモンテカルロシミュレーションをしてみる【後編】

1. はじめに

この記事は以下の記事の後編です．

https://zenn.dev/taiki_haga/articles/00b424cd192bee

ここでは前編で紹介した資産運用シミュレーターの詳細を説明していきます．

やりたいことをまとめると次のような感じになります：

1. S&P500などの株価指数のデータを入手する．
2. 過去の株価のリターンをうまくフィットできる確率モデルを決定する．
3. 確率モデルを使って多数のリターン時系列を生成する．
4. リターンから資産額の時系列を計算する．
5. 各月の資産額の分布を可視化する．

以上を順に解説していきます．

なおタイトルにもあるように，ここではJulia言語を使います．読者はJuliaの基本的な使い方は知っているものとします．

2. 株価指数のデータの入手と可視化

代表的な株価指数には，日経平均やS&P500，あるいはオールカントリーのインデックスファンドでベンチマークとして利用されるMSCI指数などがあります．ここではアメリカの有名企業をカバーしたS&P500を利用しましょう．

まずは過去数十年間のS&P500の株価データをダウンロードします．例えば，以下のStooqというサイトが便利です：

https://stooq.com/q/d/?s=^spx&c=0

日次か月次か，期間をいつからいつまでにするか，などいろいろ設定できます．ここでは，1960年から2025年までの月次データをcsvファイルとしてダウンロードしました．このファイルをsp500.csvとします．

Juliaでcsvファイルからデータを読み込むには，CSVとDataFramesというライブラリを使います．CSV.readという関数を使ってファイルから読み込んだデータフレームをsp500としましょう．

using CSV
using DataFrames
sp500 = CSV.read("sp500.csv", DataFrame)

1ヶ月ごとの始値（Open），最高値（High），最安値（Low），終値（Close），合計株価（Volume）が並んでいます．

さて，とりあえず1960年から2025年まで長めのデータを取ってきましたが，実際のところモデルの構築にどこまで遡ったデータを使うのかは難しい問題です．

当然ながら，経済とは非定常なプロセスです．製造業が稼ぎ頭だった60年代と巨大IT企業が支配する現代とでは経済や市場のあり方がまったく違いますし，ブレトン・ウッズ体制の終わりや証券取引の電子化といった金融制度の変化もあります．このような様々な社会変化を経験してきた65年間の株価データを，単一の確率モデルでフィッティングしてしまってよいのか疑問です．かといって，ここ数年間のデータに限定してしまうと，統計的な有意性を担保できるだけのサンプル数が確保できません．

ここでは便宜的に，1985年から2025年までの40年間のデータを使うことにしましょう．特に深い理由はありませんが，現代に続く情報化時代の幕開けといっていいのが80年代後半からではないでしょうか．

というわけで，過去40年分の始値のデータを取り出して，index_dataという配列に入れます．

index_data = sp500.Open[end-479:end]

まずはこのindex_dataをPlotsライブラリを使って可視化してみましょう．

using Plots
plot(index_data, xlabel="month", ylabel="index")

なんと，この40年間で30倍以上になっています！

限りある資源のことや地球環境への負荷を考えると，この成長が果たして持続可能なのか不安になってきますが，未来のことはわからないので，過去数十年間の傾向が今後も継続するものと仮定してシミュレーションをするしかありません．

さて，上のグラフを眺めると，いくつか特徴的な上昇・下落局面が見られますね．180ヶ月目（2000年ごろ）に見られるピークはドットコム・バブルでしょうか．また，270ヶ月目（2008年ごろ）の急落はリーマンショックですね．直近40ヶ月の急落と急回復はCOVID-19パンデミックによるものです．

次に月次収益率（リターン）を計算します．$t$ヶ月時点の株価を$P_t$とすれば，リターン$r_t$は以下のように定義されます：

$$r_t = \ln \frac{P_t}{P_{t-1}} \tag{1}$$

なお，自然対数$\ln$を取るのは慣習であり，深い理由はありません．株価$P_t$が幾何ブラウン運動と呼ばれる確率過程に従うならば，このように定義したリターンは正規分布に従うことが知られています．ただ，実際の株価の振る舞いは，幾何ブラウン運動とは質的に異なることが多いです．

リターンreturns_dataを計算してプロットするには以下のように書けばいいです：

log_index = log.(index_data)
returns_data = diff(log_index)
plot(returns_data, xlabel="month", ylabel="return")

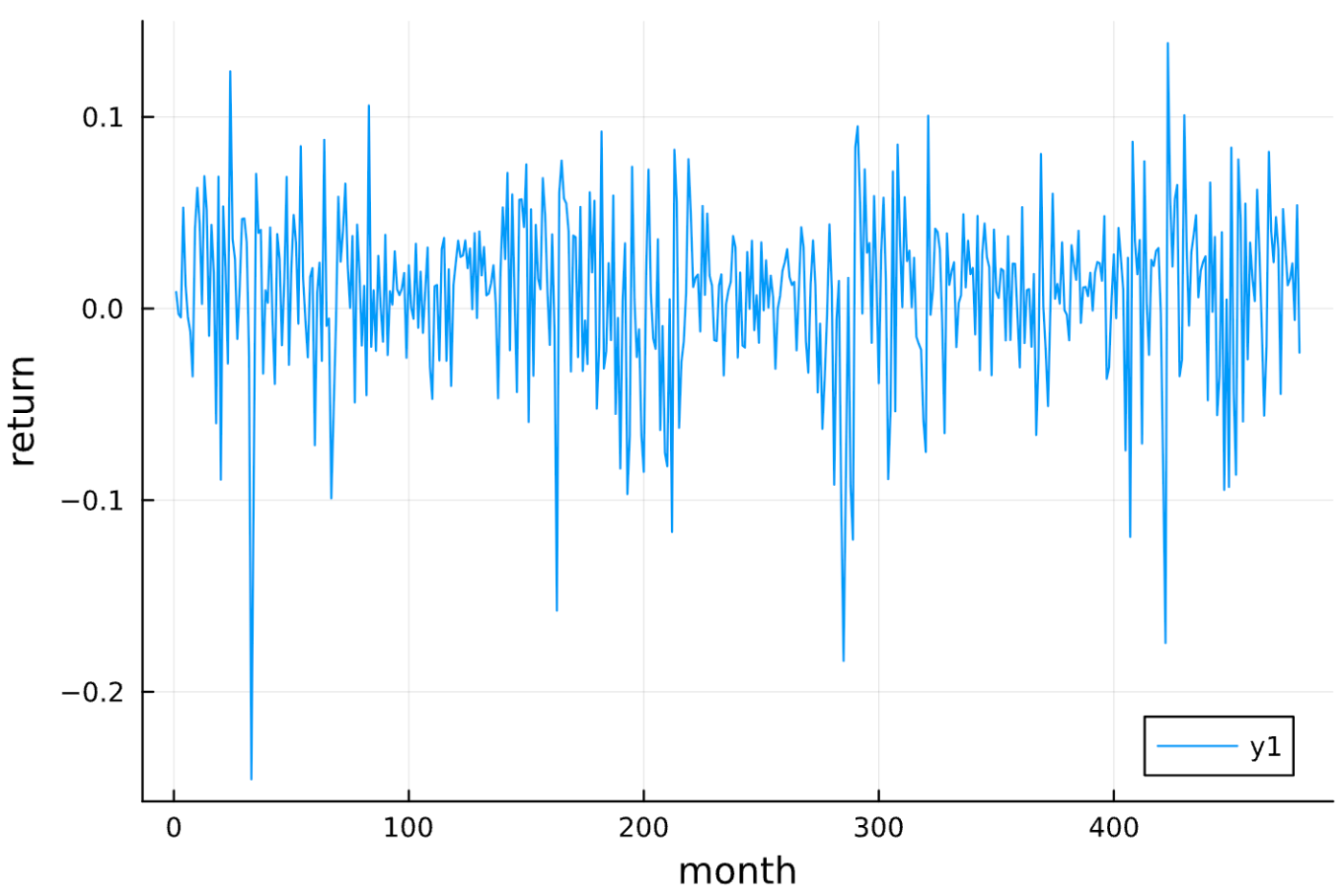
このリターンのグラフを見ると，変動が激しい時期と穏やかな時期が混在していることがわかります．ドットコム・バブルの崩壊やリーマンショックの直後に特に変動が激しくなっていますね．このように，リターンの変動（これをボラティリティといいます）が大きい時期と小さい時期がかたまる傾向をボラティリティ・クラスタリングと呼びます．

先ほど話した幾何ブラウン運動では，ボラティリティは時間に依存しない定数となっています．そのため，現実のリターンに見られるボラティリティ・クラスタリングを再現するには，より洗練された確率モデルが必要となります．

さて，リターンの時系列は平均値のまわりでプラス方向にもマイナス方向にもランダムにゆらいでいるように見えます．ここで気になるのは，ある月の$r_t$と次の月の$r_{t+1}$とがどの程度関連しているのかということです．それを見るためには，以下のような自己相関関数$C(t)$を計算するのが便利です：

$$C(t)=\frac{\langle (r_\tau - \bar{r}) (r_{\tau + t} - \bar{r}) \rangle_\tau}{\langle (r_\tau - \bar{r})^2 \rangle_\tau} \tag{2}$$

ここで$\langle A_\tau \rangle_\tau = (1/T) \sum_{\tau=1}^{T} A_\tau$は時間平均を表し，$\bar{r}=\langle r_\tau \rangle_\tau$はリターンの平均値です．自己相関関数$C(t)$の$t$をラグといいます．もし，$C(1)$が正の値を取るならば，$r_{t+1}$は$r_t$と近い振る舞いを示すことになります．これは言い換えれば，今月のリターンから来月のリターンがある程度予測できることを意味します．なお，上の定義式では，$C(0)=1$となることに注意します．

時系列データの自己相関関数を計算するには，StatsBaseというライブラリのautocor関数を使います．リターンの自己相関関数をプロットしてみましょう．

using StatsBase
returns_autocor = autocor(returns_data, demean=true)
max_lag = length(returns_autocor) - 1
plot(0:max_lag, returns_autocor, xlabel="lag", ylabel="autocorrelation")

autocor関数のdemean=trueというオプションは，上の定義式のように平均値を引くことを意味します．なお，ラグの最大値はオプションで指定することもできますが，デフォルトでは時系列データの長さから最適な値を勝手に決めてくれるようです．

このグラフから，ラグが1以上の自己相関関数の値はほとんどゼロになることがわかりますね．つまり，連続する月のリターンの間には相関がないことになります．

この事実は，インデックス投資で平均以上の利益を出したいと思っている人には悪いニュースかもしれません．自己相関関数がゼロということは，過去のリターンから未来のリターンが平均より上になるか下になるかを予測することはできないことを意味します．株価のチャートをにらんで，売りや買いのタイミングをどんなに工夫しても，長期的には平均的なリターンに収束するということですね．

なお，上のような予測不可能性はS&P500のような市場全体の傾向を総合した株価指数には当てはまっても，特定の企業の個別株には当てはまらない可能性があります．個々の株価は非自明な自己相関を持っていても，それらすべてを足し合わせた総合指数は，よりランダムで予測不可能になるというのはありそうな話です．

3. ARCHモデル，GARCHモデル，EGARCHモデル

上で見たように，リターンの変動の大きさ（ボラティリティ）は時間と共に確率的に変動します．このようなプロセスを記述するためには，幾何ブラウン運動を超えた，より複雑なモデルが必要になります．それが以下で紹介するARCHモデル，およびそれから派生したGARCHモデルとEGARCHモデルです．

ARCHとは，"Autoregressive Conditional Heteroscedasticity"の略です（「アーチモデル」と読みます）．日本語では「分散自己回帰モデル」などと呼ばれます．分散とはボラティリティのことです．それが自己回帰的であるとは，現在のボラティリティが過去のボラティリティの線形結合で書けるということを意味します．

ARCHモデルは1982年にロバート・エングル（Robert F. Engle）によって提案されました．彼はこの功績で2003年にノーベル経済学賞を受賞しています．

まず，時刻$t$におけるリターン$r_t$が，平均リターン$\mu$とボラティリティ$\sigma_t$を使って以下のように書けるとします：

$$r_t = \mu + \sigma_t z_t \tag{3}$$

ここで$z_t$は平均$0$で分散$1$の独立な正規乱数です．これは平均値$\mu$のまわりを標準偏差$\sigma_t$でゆらいでいるような時系列を表します．$z_t$は独立なので，異なる時刻における$r_t-\mu$の間に相関はありません．ちなみに，ファイナンスの分野では$\sigma_t z_t$のことを「イノベーション」と呼んだりします．

もし，ボラティリティ$\sigma_t$が時間$t$に依存しない定数$\sigma$ならば，これは幾何ブラウン運動になります．しかし，実データはボラティリティ$\sigma_t$が時間と共に変動することを示唆しています．

ARCHモデルでは，ボラティリティ$\sigma_t$が以下のような式にしたがうと仮定します：

$$\sigma_t^2 = \omega + \alpha \sigma_{t-1}^2 z_{t-1}^2. \tag{4}$$

ここで$\omega$と$\alpha$は正のパラメータです．ただし$\sigma_t$が発散しないためには，$\alpha<1$という条件が必要です．

この式の意味を理解するため，仮に$z_t$がずっと$1$の値を取る場合を考えましょう．このとき，$\sigma_t^2$は

$$\sigma_t^2 = \frac{\omega}{1-\alpha} + \alpha^t \left( \sigma_0^2 - \frac{\omega}{1-\alpha} \right) \tag{5}$$

と書けます．これより，$\sigma_t^2$は$-1 / \ln \alpha$程度の時間スケールで定常値$\omega/(1-\alpha)$に収束することになります．

実際には，$z_t$はランダムに変動します．ある時刻で$z_t$がたまたま極端に大きな値を取ったとすると，その後$-1 / \ln \alpha$程度の間ボラティリティが大きな期間が続くということになります．この振る舞いは，「株価が急落した後，リターンが激しく変動する期間がしばらく続く」という観察と整合していますね．

ARCHモデルの発展形でGeneralized ARCH (GARCH)モデルがあります（「ガーチモデル」と読みます）．このモデルではボラティリティ$\sigma_t$は以下のような式にしたがいます：

$$\sigma_t^2 = \omega + \beta \sigma_{t-1}^2 + \alpha \sigma_{t-1}^2 z_{t-1}^2. \tag{6}$$

$\beta$もまた正のパラメータですが，$\sigma_t$が発散しないためには$\alpha+\beta<1$という条件が必要です．$\beta$を含む項は$\sigma_t^2$の自己回帰的な効果を表しています．

なお，上で説明したARCHモデルとGARCHモデルの定義では，時刻$t$のボラティリティがその一つ前の時刻$t-1$の量によって決まるとしました．もちろん，さらに遡って$k \geq 2$だけ前の時刻$t-k$の量からの寄与を含めるように一般化することもできます．

さて，以上のARCHモデルとGARCHモデルには共通する欠点があります．一般に株式市場では，リターンが上がった場合よりも，リターンが下がった場合の方が，その直後のボラティリティがより増大することが知られています．投資家は良いニュースより悪いニュースに敏感に反応するということですね．これをレバレッジ効果と呼びます．ARCHモデルとGARCHモデルでは，$z_{t-1}$が正でも負でもボラティリティ$\sigma_t$に与える影響は同じですから，レバレッジ効果を説明することはできません．

こうした問題を解決するために導入されたのが，今回のシミュレーションで使ったExponential GARCH (EGARCH)モデルです．このモデルでは，ボラティリティは以下の式にしたがいます：

$$\log(\sigma_t^2) = \omega + \gamma z_{t-1} + \beta \log(\sigma_{t-1}^2) + \alpha (|z_{t-1}| - \sqrt{2/\pi}). \tag{7}$$

この式の$\exp$を取ることで$\sigma_t^2=\cdots$の形にすると，右辺に$\exp(\gamma z_{t-1})$のような項が現れます．これがレバレッジ効果に相当する非対称性を生みます．もし$\gamma<0$なら，$\exp(\gamma z_{t-1})$は$z_{t-1}<0$のときの方が，$z_{t-1}>0$のときより大きくなるからです．

なお，EGARCHの式(7)で最後に現れる$\sqrt{2/\pi}$は$|z_{t-1}|$の期待値です．$\alpha$は$z_{t-1}$のゆらぎの大きさが直後のボラティリティにどの程度影響を及ぼすのかを特徴づけるパラメータです．ところで，この最後の項は$\alpha (z_{t-1}^2 - 1)$でも良さそうな気がします．原著論文を読んでないので詳細はわかりませんが，$z_{t-1}^2$ではなく$|z_{t-1}|$を使っているのは，大きな$z_{t-1}$に対して$\exp(z_{t-1}^2)$が$\exp(|z_{t-1}|)$に比べてあまりにも急激に増加するからなのかもしれません．

さて，これからやりたいことはS&P500の過去のデータをうまく再現するようなEGARCHモデルのパラメータを決定することです．そのために最尤推定法を使います．推定するべきパラメータ$\mu$, $\omega$, $\alpha$, $\beta$, $\gamma$をまとめて$\theta$と書くことにしましょう．時刻$t=1$から$T$までのリターンのデータ$\{r_t\}_{t=1,...,T}$が与えられているとして，対応する尤度関数は式(3)より以下のように書けます：

$$P(\{r_t\}_{t=1,...,T}|\theta) = \prod_{t=1}^T (2\pi \sigma_t^2)^{-1/2} \exp \left[- \frac{(r_t - \mu)^2}{2\sigma_t^2} \right]. \tag{8}$$

ただし，$\sigma_t^2$は過去のリターン$r_1, ..., r_{t-1}$に依存することに注意します：

$$\sigma_t^2 = \sigma_{t-1}^{2\beta} \exp \left[\omega + \gamma \left(\frac{r_{t-1} - \mu}{\sigma_{t-1}}\right) + \alpha \left( \frac{|r_{t-1} - \mu|}{\sigma_{t-1}} - \sqrt{\frac{2}{\pi}} \right) \right]. \tag{9}$$

初期時刻における分散$\sigma_1^2$を適当な値に固定すれば，尤度関数$P(\{r_t\}_{t=1,...,T}|\theta)$を上の式から計算することができます．あとは，これを最大にするパラメータ$\hat{\theta}$を求めればいいわけです．

上記の尤度関数はとても複雑な形をしていて最適化するのは大変そうですが，幸い便利なライブラリがあります．それがARCHModels.jlです．returns_dataというデータをEGARCHモデルでフィットするには以下のように書くだけでOKです：

using ARCHModels
fit(EGARCH{1,1,1}, returns_data)

{1,1,1}というオプションは，式(7)で$\alpha$, $\beta$, $\gamma$の項が現時刻の一つ前の量を含むことを意味します．これらをもっと大きな数字にすれば，より過去の影響を反映するモデルになるわけです．推定されたパラメータ$\mu$, $\omega$, $\alpha$, $\beta$, $\gamma$は以下のようになりました：

Estimateが推定値で，Std.Errorが標準誤差です．Pr(>|z|)は，仮にその項が存在しない（パラメータがゼロ）としたとき，それにもかかわらず当該項が存在すると判定されてしまう確率です．この値が非常に小さいということは，当該パラメータが有意にゼロではないことを示唆します．

ARCHModelsがどうやって尤度関数の最適化を行なっているのかは，ライブラリの開発者による論文に詳しいです．どうも，Optimという有名な最適化ライブラリを使っているようですね．自動微分によって尤度関数の勾配を求めたあと，BFGSアルゴリズムを使ってパラメータの更新を行うといった感じみたいです．

結果として，S&P500をフィットするEGARCHモデルのパラメータとして

$$\mu = 0.00692, \: \omega = -2.293, \: \alpha = 0.337, \: \beta = 0.638, \: \gamma = -0.345. \tag{10}$$

が得られました．

4. リターン時系列の計算

さて，S&P500のリターンをうまく再現する確率モデルが得られました．このモデルを使えば，S&P500のリターンと似たような統計的性質を持つ時系列をいくらでも生成することができます．そのために，与えられたパラメータについてEGARCHモデルの時系列（長さT）を計算する関数simulate_egarchを定義しましょう．

function simulate_egarch(
    T::Int,
    ω::Float64,
    α::Float64,
    β::Float64,
    γ::Float64,
    μ::Float64,
    T_warmup::Int
)
    # ウォームアップを含むシミュレーションの長さ
    T_total = T + T_warmup

    # 各配列の初期化
    r_total = zeros(T_total)     # ウォームアップを含むリターン
    σ_total = zeros(T_total)     # ウォームアップを含むボラティリティ
    ln_σ2_total = zeros(T_total) # ウォームアップを含む対数ボラティリティ

    # 標準正規分布の絶対値|z_t|の平均値
    E_abs_z = sqrt(2 / π)

    # 対数ボラティリティの初期化（任意）
    ln_σ2_total[1] = ω

    # 正規乱数
    z_total = randn(T_total)

    for t in 1:T_total
        if t > 1
            # ln(σ_t^2)をアップデート
            ln_σ2_total[t] = ω + β * ln_σ2_total[t-1] + γ * z_total[t-1] + α * (abs(z_total[t-1]) - E_abs_z)
        end

        # σ_tをアップデート
        σ_total[t] = sqrt(exp(ln_σ2_total[t]))

        # r_tをアップデート
        r_total[t] = μ + σ_total[t] * z_total[t]
    end

    # ウォームアップ期間を除く
    r = r_total[T_warmup+1:end]
    σ = σ_total[T_warmup+1:end]

    return r, σ
end

初期値の影響を排除するため，ウォームアップ期間T_warmupを設けています．また，リターンに加えてボラティリティの時系列も返すようにしています．試しに，S&P500のリターンをフィットすることで得られたパラメータ(10)を使ってリターンとボラティリティの時系列を計算してみたのが下の図です．ボラティリティ・クラスタリングが再現できていますね．

後で使うので，長さTのリターン時系列のみを返す関数return_simulatorを定義しておきましょう：

function return_simulator(T::Int)
    # S&P500を再現するEGARCHモデルのパラメータ
    ω = -2.293           # ω
    α = 0.337            # α - magnitude effect
    β = 0.638            # β - persistence
    γ = -0.345           # γ - asymmetry
    μ = 0.00692          # μ - average return

    T_warmup = 100       # ウォームアップ期間

    returns_simulated, volatility_simulated = simulate_egarch(T, ω, α, β, γ, μ, T_warmup)

    return returns_simulated
end

リターン$r_t$から株価$P_t$を求めたければ，リターンの定義式(1)に立ち戻りましょう．return_simulatorでリターン時系列$r_t$を計算したら，あとは前の月の株価に$e^{r_t}$を掛けていくだけですね．10個のリターン時系列について，株価の変動をプロットしたものが以下の図です．最初の月の株価が1になるように規格化しています．黒の線が実際のS&P500の値動きです．実データに見られるような，株価の急落がよく再現されていますね．ただ，シミュレーション期間が長くなると，最終的な株価はかなり広い範囲にばらつくことが見て取れます．

5. 資産額の時系列の計算

さて，これで必要なパーツはそろいました．あとはリターンの時系列から資産額を計算するコードを書けば完成です．指定するべきパラメータは以下の4つです：

• 投資期間 total_month（月）
• 初期投資額 initial_investment（万円）
• 毎月の積立額 monthly_investment（万円）
• 累計投資上限 total_investment（万円）

まず1ヶ月目にinitial_investment万円を投資して，2ヶ月目からmonthly_investment万円ずつ積み立てていく形にします（initial_investmentはゼロでも構いません）．累計投資額が total_investment万円に達したら，それ以降の積立額はゼロになります．

上で定義した関数return_simulatorを実行することで月次リターン$r_t \: (t=1,2,...)$が得られたとしましょう．すると，$t$ヶ月時点での資産額は次の式で計算できます：

$$V_{t} = e^{r_t} (V_{t-1} + A_{t-1}) \tag{11}$$

ここで$A_t$は$t$ヶ月目の積立額で，その時点での累計投資額が total_investment万円以下ならmonthly_investment万円で，それを超えたらゼロです．

まず，累計投資額を計算する関数calc_invested_cumulativeを定義します．これは上記の投資プランのもとで，各月末における累計投資額を一次元配列で返す関数です．これは単に，初期投資額initial_investmentに毎月monthly_investmentを，上限total_investmentに達するまで足し上げていくだけですね．

function calc_invested_cumulative(
    total_month::Int,
    initial_investment::Float64,
    monthly_investment::Float64,
    total_investment::Float64
)
    invested_cum = zeros(total_month)
    invested_so_far = 0.0

    for t in 1:total_month
        if t == 1
            # 初月に初期投資
            invested_so_far += initial_investment
        else
            # 2ヶ月目以降は monthly_investment を追加
            if invested_so_far < total_investment
                remain = total_investment - invested_so_far
                invest_now = min(monthly_investment, remain)
                invested_so_far += invest_now
            end
        end
        invested_cum[t] = invested_so_far
    end

    return invested_cum
end

各月末における累計投資額が入った一次元配列をinvested_cumとしました．いよいよ資産額を計算する関数simulate_portfolioを定義しましょう．これは累計投資額invested_cumと任意の自然数n_simsを引数として，n_sims個の資産額時系列を二次元配列として返すような関数です．

function simulate_portfolio(invested_cum::Vector{Float64}, n_sims::Int)
    total_month = length(invested_cum)
    asset_paths = zeros(n_sims, total_month)
	
    for sim in 1:n_sims
        # 月次リターン系列
        r_series = return_simulator(total_month)

        # 各月の資産額を計算
        value = 0.0  # 前月末の資産額（最初は0とし，1ヶ月目で初期投資分を加える）
        for t in 1:total_month
            # 追加投資額 = 今月までの累計 - 前月までの累計
            additional = (t == 1) ? invested_cum[1] : (invested_cum[t] - invested_cum[t-1])

            value += additional         # 今月分の投資額を加える
            value *= exp(r_series[t])   # 今月のリターンを反映

            asset_paths[sim, t] = value
        end
    end

    return asset_paths
end

6. 資産額の可視化

資産額の時系列データasset_pathsが得られたので，これを可視化してみましょう．具体的には，各月での資産額の中央値と第1四分位数・第3四分位数をプロットしたいです．まずはasset_pathsから，これらの統計量を計算します：

using Statistics

month_median = zeros(total_month)
month_q1 = zeros(total_month)
month_q3 = zeros(total_month)
for t in 1:total_month
    col = asset_paths[:, t]
    month_median[t] = median(col)
    month_q1[t] = quantile(col, 0.25)
    month_q3[t] = quantile(col, 0.75)
end

quantile(x, 0.25)は配列xの下から25%の値を取得することを意味します．もちろん，median(x)は中央値を計算する関数ですね．これらの関数はStatisticsライブラリに含まれますが，これはJuliaの標準ライブラリなので，改めてインストールする必要はありません．

グラフのプロットにはPyPlotライブラリを使います．第1四分位数から第3四分位数までを青色で塗りつぶして，そこに中央値を黒の実線でプロットします．さらに，累計投資額も赤の破線で示すことにしましょう．

figure()
# Q1~Q3の帯を塗りつぶし
fill_between(
    1:total_month, 
    month_q1, 
    month_q3, 
    color="lightblue", 
    alpha=0.3, 
    label="Q1–Q3 range"
)

# 中央値をプロット
plot(1:total_month, month_median, color="black", linewidth=2, label="Median")

# 投資累計額をプロット
plot(1:total_month, invested_cum, color="red", linestyle="--", linewidth=2, label="Invested so far")

xlabel("Month")
ylabel("Asset Value (¥10⁴)")
title("Asset Growth Simulation")
legend(loc="upper left")

gcf()

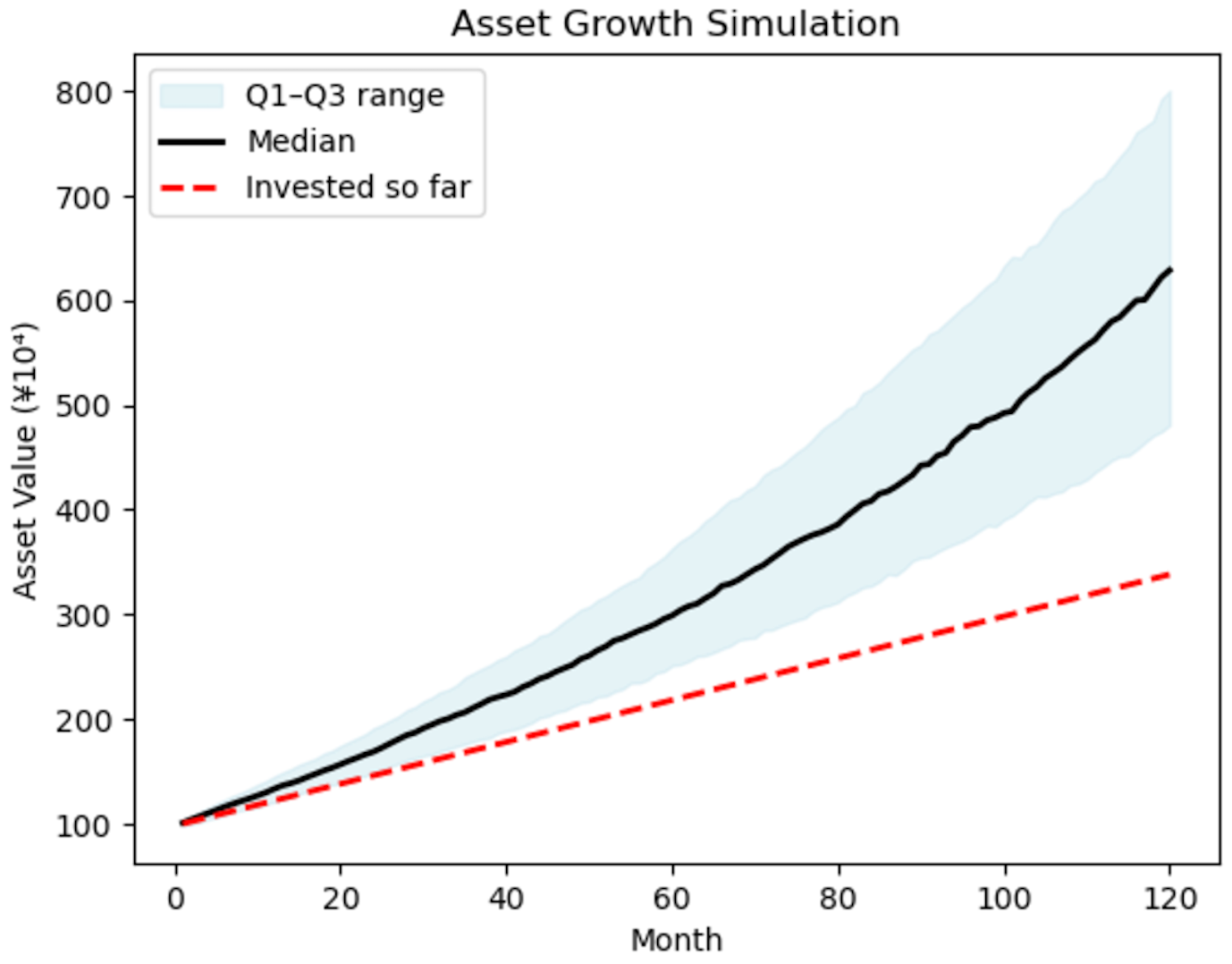
コードの意味はだいたいわかるかと思います．投資期間が120ヶ月で初期投資額が100万円，毎月の積立額が2万円の場合には，以下のようになります．

7. おわりに

この記事では，EGARCHモデルによる金融データの解析とモンテカルロシミュレーションをJulia言語を使ってやってみました．ARCHModelsライブラリのおかげで，とても簡単にできましたね．

この記事では省きましたが，本来のデータ分析ではモデル選択のプロセスが必要になります．幾何ブラウン運動やARCHモデル，EGARCHモデルなど様々なモデルの中で，どれが最もデータを精度良くフィットできるのかを比較するわけですね．この際には，赤池情報量規準（AIC）やベイズ情報量規準（BIC）などがよく使われます．

実はARCHModelsライブラリには，AICを使って自動的に最適なモデルを選択するツールが用意されています．こうしたツールを活用すれば，さらに精度の高いシミュレーションが可能になるかもしれません．

なお，この記事を書くにあたって以下の文献が参考になりました：

横内大介，青木義充，「現場ですぐ使える時系列データ分析」（技術評論社 ，2014年）

注意・免責事項

• 本シミュレーターは，あくまで金融時系列の確率的生成モデルに基づくものであり，将来の実際の運用成績を保証するものではありません．
• 現実の市場では突発的なイベントや非定常的な構造変化が起こり得るため，シミュレーション結果はあくまで参考値として扱ってください．
• 投資判断は自己責任で行い，必要に応じて専門家の助言を求めてください．