Juliaで資産運用のモンテカルロシミュレーションをしてみる【前編】
1. はじめに
みなさん,NISAで資産運用はしていますか?
積立投資で特に人気があるのがS&P500などの市場全体の株価指数に連動するインデックスファンドです.過去30年間のS&P500をベンチマークとした投資信託の年平均利回りは約8%とのことです.もし100万円を年8%の利回りで20年間運用すれば,最終的には470万円ほどになる計算です.
しかし,実際の株価はきれいな指数関数的カーブを描くわけではなく,経済のトレンドに振り回されて激しく変動するものです.株価が何らかの確率過程に従うと仮定するならば,投資信託の運用益も確率変数とみなすべきです.当然知りたくなるのは運用益の確率分布でしょう.
例えば100万円を20年間運用するとして,最終年度の資産額が700万円を超える確率は何%でしょうか?もっと気になるのは,運悪く市場の大暴落が起こって資産額が元本の100万円を下回ってしまうリスクは何%あるのでしょうか?
Web上には様々な投資シミュレーターが公開されていますが,これらは指定された利回りのもとでの平均的な運用益は教えてくれても,その平均値のまわりで運用益がどのくらいバラつくのかは教えてくれません.
そこでこの記事では,Julia言語を使ってインデックス投資のモンテカルロシミュレーションにトライしたいと思います.これによって各月における資産額のヒストグラムが得られるため,中央値や標準偏差などの統計量を評価することができます.
なお,この記事ではJuliaの基本的な使い方を知っている読者を想定していますが,Pythonなどの高水準言語で数値計算をしたことがある人であれば,おおまかなアイディアを理解するのに支障はないはずです.
2. シミュレーションの概要
- 1985年~2025年のS&P500のデータ(ドルベース)を利用してモデルを構築しています.
- 過去40年間の月次リターンが定常な確率過程に従うとみなし,この傾向が今後も続くことを仮定しています.
- S&P500に完璧に連動するインデックスファンドを想定しており,為替の影響や手数料は考慮していません.
- 月次リターン時系列のモデル化にはEGARCHモデル (Exponential Generalized Autoregressive Conditional Heteroscedasticity model)を使っています.このモデルの詳しい説明は後編でする予定です.
3. デモンストレーション
シミュレーションの詳細な説明に入る前に,とりあえずシミュレーターの簡単なデモンストレーションから始めたいと思います.このシミュレーターはS&P500に連動するインデックスファンドに積立投資したときの資産額の分布を計算してくれます.
Pluto.jl というライブラリを使って,シミュレーターの簡単なUIを作ってみました.これはJupyter Notebookのようなツールなのですが,スライドを動かしてパラメータを設定したりとインタラクティブな操作が可能です.
興味がある方は,以下のレポジトリからシミュレーターをダウンロードして遊んでみてください.
さて,シミュレーターの上部には投資のパラメータを設定するスライドが並んでいます.

入力すべきパラメータは以下の通りです:
- 投資期間(カ月)
- 初期投資額(万円)
- 毎月の積立額(万円)
- 総投資額(万円)
なお,NISAでは非課税投資枠の上限は1800万円なので,このシミュレーターでも総投資額の上限を1800万円に設定しています.累積投資額が総投資額を超えると,それ以降の月の積立額は投資期間が終わるまでゼロとなります.
ここでは,初期投資100万円で毎月2万円積み立てていく場合を想定しましょう.パラメータを入力すると,確率モデルにしたがって1000個の資産額の時系列が生成されます.

これを元に各月での資産額の中央値と第1四分位数・第3四分位数をプロットしてくれます.第1四分位数は下から25%,第3四分位数は下から75%の投資成績に相当します.

つまり,初期投資100万円で毎月2万円積み立てていくと,10年後の資産額の中央値が約630万円,少し運の悪いシナリオでは480万程度になるということがわかります.
また,最終資産額の分布も出してくれます.

右に長い裾を引いたような分布になり,正規分布からはほど遠い形をしていますね.このような分布の場合,平均値は中央値や最頻値よりもだいぶ大きめに出てしまうことに注意です.
最後に,運悪く元本割れが起こる確率も出してくれます.なお元本とはこの場合,初期投資額 + 積立額 × (投資期間 - 1) となります(積立は2カ月目から始めると想定しています).
4. 投資プランの比較
この投資シミュレーターが真価を発揮するのは異なる投資プランを比較するときです.以下のような二つの投資プランを考えてみましょう.
- 積立投資:毎月1万円を10年間(120カ月)積み立てる.
- 一括投資:最初の月に120万円投資して,10年間放置する.
これらの投資プランのうち,元本割れ(資産額が投資額を下回る)のリスクが低いのはどちらでしょうか?
もちろん,最終資産額の期待値が大きいのは一括投資ですよね.より多くの資産を長い時間運用できるからです.しかし,巷では積立投資の方がリスクが少ないと言われています.理由は以下の通りです:
- 一括投資の場合,投資成績が最初に投資した瞬間の株価に大きく左右されるため,最終資産額のばらつきが大きくなる.もし運悪く株価が異常に高騰している時期に一括投資してしまうと,その後株価が暴落したときに大損してしまう可能性があります.
- 積立投資の場合,株価が高いときも低いときも同じ額を積み立てていくので,長期的に見ればリターンの変動はならされて,最終資産額のばらつきは小さくなる.したがって,元本割れのリスクは抑えられる.
つまり,まとめると
- 一括投資 → 期待値:大 & ばらつき:大
- 積立投資 → 期待値:小 & ばらつき:小
というわけです.ただこれだけでは,どちらの方が元本割れのリスクが低いのか微妙なところですね.
そもそも,私がこのシミュレーターを作ろうと思い立ったきっかけが上のような疑問でした.
奥さんとNISAについて話していたときのことです.彼女はそこそこお金があるのに旧NISAから引き続き月3万円をコツコツ積み立てていました.そこで私が,せっかく貯金もあることだし,成長投資枠を使って一括投資した方がよいのではと提案してみました.ところが彼女が主張するには,上に述べたような理屈で積立投資の方がリスクが少ないから安心とのことです.なるほど,たしかに…と反論できませんでした😅
結局,二つの投資プランのリスクを評価するには資産額の期待値を比べるだけではダメで,そのゆらぎも考慮する必要があります.それではさっそく,シミュレーターを使って調べてみましょう.
積立投資の場合
毎月1万円を10年間(120カ月)積み立てた場合の資産額を見てみましょう.
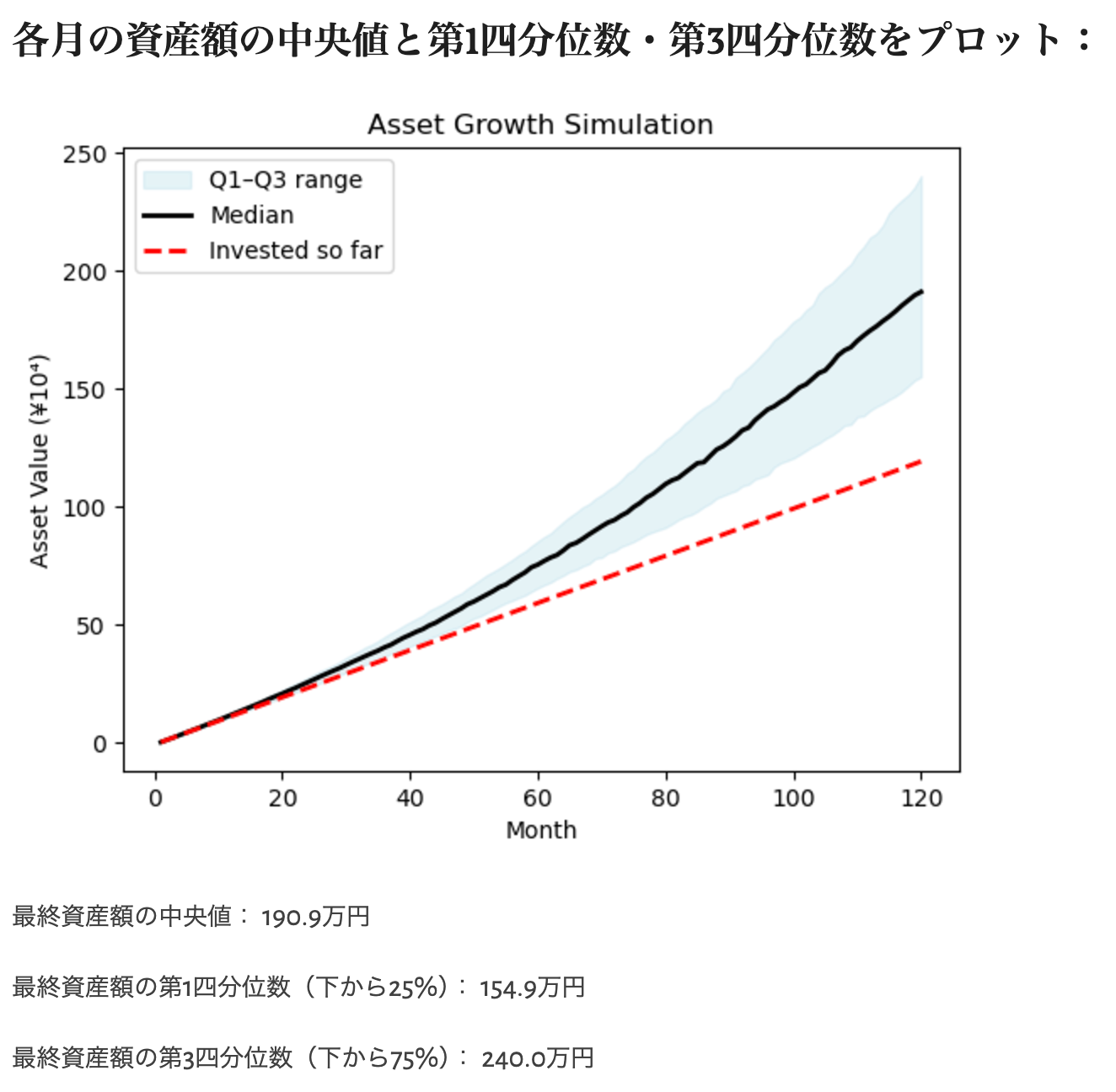
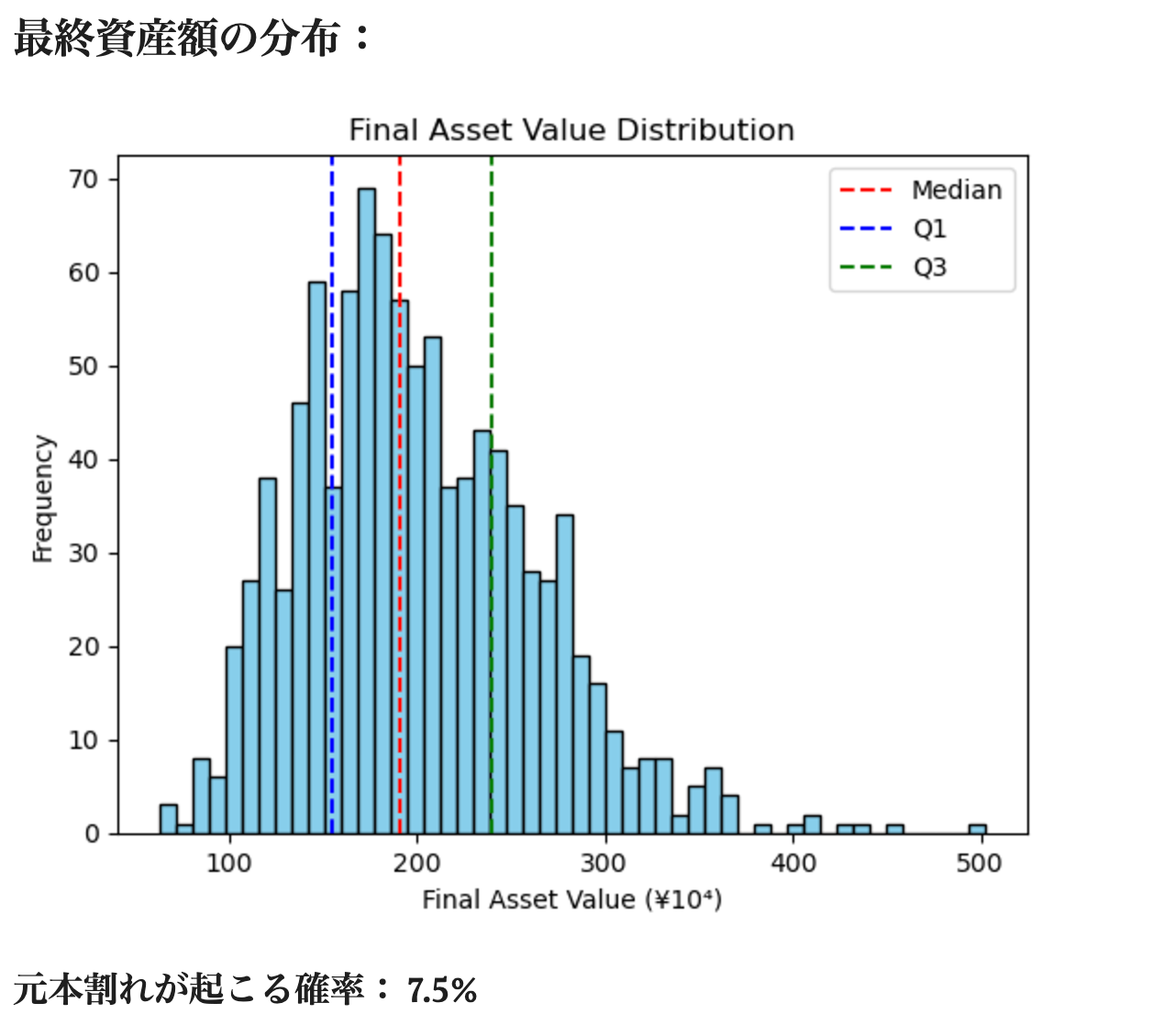
最終資産額は200万円プラスマイナス40万円といったところでしょうか.中央値まわりのばらつきの幅は40%ほどです.元本割れが起こる確率は7.5%となりました.
一括投資の場合
次に最初の月に120万円投資して,10年間放置した場合を見てみましょう.

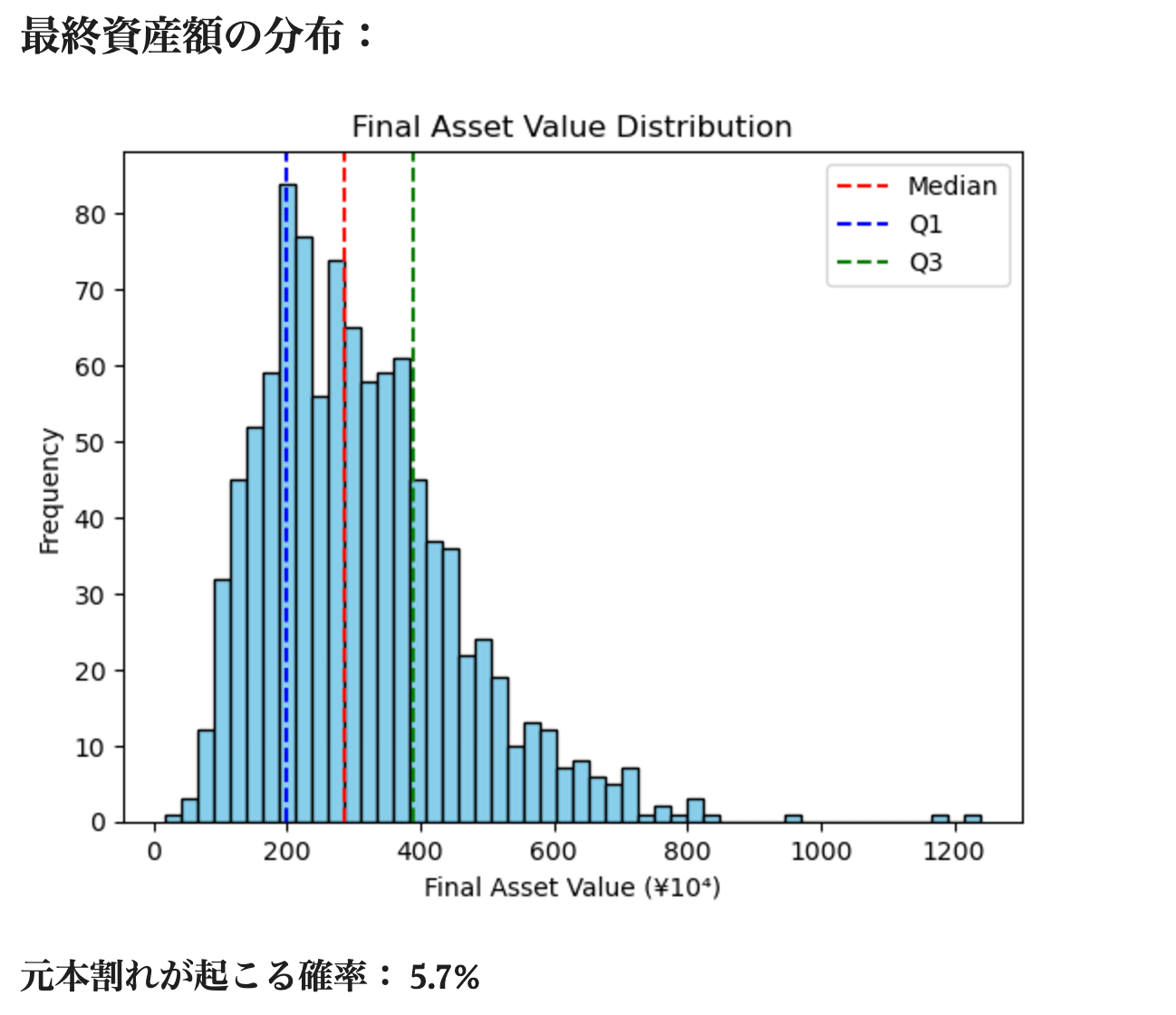
最終資産額は300万円プラスマイナス100万円といった感じです.中央値まわりのばらつきの幅は60%ほどです.
予想通り,積立投資より一括投資の方が資産額のばらつきは大きいです(40%に対する60%).一方で,一括投資の場合に元本割れが起こる確率は5.7%となり,積立投資の場合(7.5%)よりも低くなりました.
ちなみに,1000個のモンテカルロサンプルのうち一番小さな最終資産額は,積立投資の場合60万円くらいで,一括投資の場合30万円程度となりました.
以上から次のことがわかります.
- 資産額の中央値:積立投資 < 一括投資 → 一括投資の勝ち!
- 資産額の相対的なばらつき:積立投資 < 一括投資 → 積立投資の勝ち!
- 元本割れの確率:積立投資 > 一括投資 → 一括投資の勝ち!
- 最も運が悪いサンプルの資産額:積立投資 > 一括投資 → 積立投資の勝ち!
意外なのは,元本割れのリスクは一括投資の方が低いということです.これは巷で言われていることとは逆ですね.なお一見すると,上記の3と4は矛盾しているように思えるかもしれません.しかし,一括投資の場合の資産分布は左右に長い裾を引く形になっていて,極端に大きい値や小さい値を取りやすいことに注意すれば,それほど不思議なことではないかもしれません.リーマンショックのような100年に一度の大不況に備えたいなら,やはり積立投資の方が安全です.
どちらの投資プランが好ましいかは個人の価値観によりますが,多くの人にとって一括投資の方がおすすめかと思います.
これで奥さんを説得できますね👍
この記事の後編では,シミュレーションの詳細を解説したいと思います.
注意・免責事項
- 本シミュレーターは,あくまで金融時系列の確率的生成モデルに基づくものであり,将来の実際の運用成績を保証するものではありません.
- 現実の市場では突発的なイベントや非定常的な構造変化が起こり得るため,シミュレーション結果はあくまで参考値として扱ってください.
- 投資判断は自己責任で行い,必要に応じて専門家の助言を求めてください.
Discussion