拡大・平行移動・回転行列で作る円形カルーセル

1. はじめに

AI エンジニアの山田です。
普段はAI開発をメインにしていて、ウェブのフロントエンドの経験はありません。
そんな私が社内のUI勉強会に参加し、 WebGL でのアニメーションに初めて挑戦した備忘録です。

今回のUI Lab #0のテーマは「カルーセルUI」です。
https://zenn.dev/studio/articles/7a1d2d294aec11

カルーセルUIを検索してみると大学時代の画像処理で学んだアフィン変換の行列演算を思い出しました。
このことをデザイナー兼フロントエンドエンジニアである小原さんに話したところ、行列やベクトルを直接操作したいのであれば生のWebGLがいいよとのことだったので、WebGLを使って行列演算で実装をしてみました。

この記事では、WebGL初心者が行列の基本（拡大・平行移動・回転）を理解してカルーセルを動かすことをゴールにしています。

小原さんがWebGLで作った戦車はこちら↓
凄い。凄すぎる...。
戦車を動かして遊べるので、仕事に疲れたときにおすすめです🔥
https://webgl-tank.tsmallfield.com/

今回私がWebGLで作成した円形カルーセルはこちら↓
https://yuyamada0917.github.io/carousel-webgl/

動画はこちら↓
https://x.com/YuYamada_opt/status/1982462003307487637

2. WebGLの座標変換の基本

WebGLとは

WebGL (Web Graphics Library)とはインタラクティブな3Dや2DのグラフィックをレンダリングできるJavaScript APIです。
https://developer.mozilla.org/ja/docs/Web/API/WebGL_API

Three.jsのようなWebGLラッパーライブラリとは違い、生のWebGLではより低レイヤーの制御が必要です。自分で頂点を定義し、シェーダーを通して描画命令を送る必要があります。

WebGLの基本概念

WebGLでは、描画するすべての3Dモデルが頂点の集合でできています。そして、それらの頂点をどのように配置し、どのように動かすかがキモです。
頂点の座標に対して行列演算を用いて「拡大」「回転」「移動」といった変換をまとめておこなうことでグ、3Dモデルを動かしたり変形したりできます。
WebGLでの座標変換は、大きく3段階に分かれます。

名称	目的	主に扱う変換
モデル変換	ワールド座標でのモデルの変形	拡大・回転・平行移動
ビュー変換	カメラ中心の座標に変換	回転・平行移動
プロジェクション変換	3Dを2D画面に投影	パースの設定（遠近感）

この記事では、上のうちモデル変換に焦点を当てます。
すなわち、モデルを三次元空間上でどう動かすかに集中します。

• 拡大：大きさを変える
• 平行移動：位置を変える
• 回転：角度を変える

これらの行列演算により座標表現を行います。
また座標系は右手系です。
右手-左手座標系について詳しく知りたい方はこちら↓
https://zenn.dev/boiledorange73/articles/0040-rhs-lhs

3. 拡大・平行移動・回転行列を理解する

3.1 同次座標系

コンピュータビジョン分野では、任意の変換を「変換行列と同次座標ベクトル積」として表すために同次座標系を用います。
平行移動では定数項部分の演算を表現するために同次座標が必要です。(3.3で説明)以降は同次座標系の4x4行列を考えます。
https://cvml-expertguide.net/terms/cv/homogeneous-coordinates/

3.2 拡大行列

拡大行列はオブジェクトの大きさを変えるための行列です。
三次元空間の任意のベクトル$p$を考えます。

$$p = \begin{bmatrix} x \\\\ y \\\\ z \end{bmatrix}$$

ベクトル$p$をx軸方向に$s_x$倍、y軸方向に$s_y$倍、z軸方向に$s_z$倍に拡大したベクトルのそれぞれの成分は$x'={s_x}​x,\,y'={s_y}​y,\,z'={s_z}​z$と表すことができます。
同次座標系にするために4x4行列に拡張すると、拡大行列は以下で表すことができます。

$$S = \begin{bmatrix} s_x & 0 & 0 & 0 \\\\ 0 & s_y & 0 & 0 \\\\ 0 & 0 & s_z & 0 \\\\ 0 & 0 & 0 & 1 \end{bmatrix}$$

3.3 平行移動行列

平行移動行列はオブジェクトの位置を動かす行列です。
同様に三次元空間の任意のベクトル$p$を考えます。このベクトルを$(t_x,t_y,t_z)$だけ平行移動すると、それぞれの成分は$x'=​x+{t_x},\,y'=​y+{t_y},\,z'=z+{t_z}$と表すことができます。
しかしながらこの行列は定数項が存在するため乗算だけでは表すことができません。
そこで同次座標系の出番です。4x4行列に拡張することで定数項を表現でき、平行行列を以下で表すことができます。

$$T = \begin{bmatrix} 1 & 0 & 0 & t_x \\\\ 0 & 1 & 0 & t_y \\\\ 0 & 0 & 1 & t_z \\\\ 0 & 0 & 0 & 1 \end{bmatrix}$$

3.4 回転行列

回転行列は、オブジェクトをある軸のまわりに回転させる行列です。
三次元空間では、x軸、y軸、軸の3つの回転軸があります。

• x軸回転：上下方向に回転(縦に回す)
• y軸回転：左右方向に回転(横に回す)
• z軸回転：奥行き方向に回転(平面上で回す)

---

x軸回転行列

x軸を中心に回転する場合、y–z平面上の点が円を描くように動きます。
任意のベクトル$p$を三角関数を用いて以下で表します。

$$p = \begin{bmatrix} x \\\\ r\cos\phi \\\\ r\sin\phi \end{bmatrix}$$

このベクトルをx軸周りに角度$\theta$だけ回転させたベクトル$p'$を考えます。この時のy-z平面は以下のように図示できます。

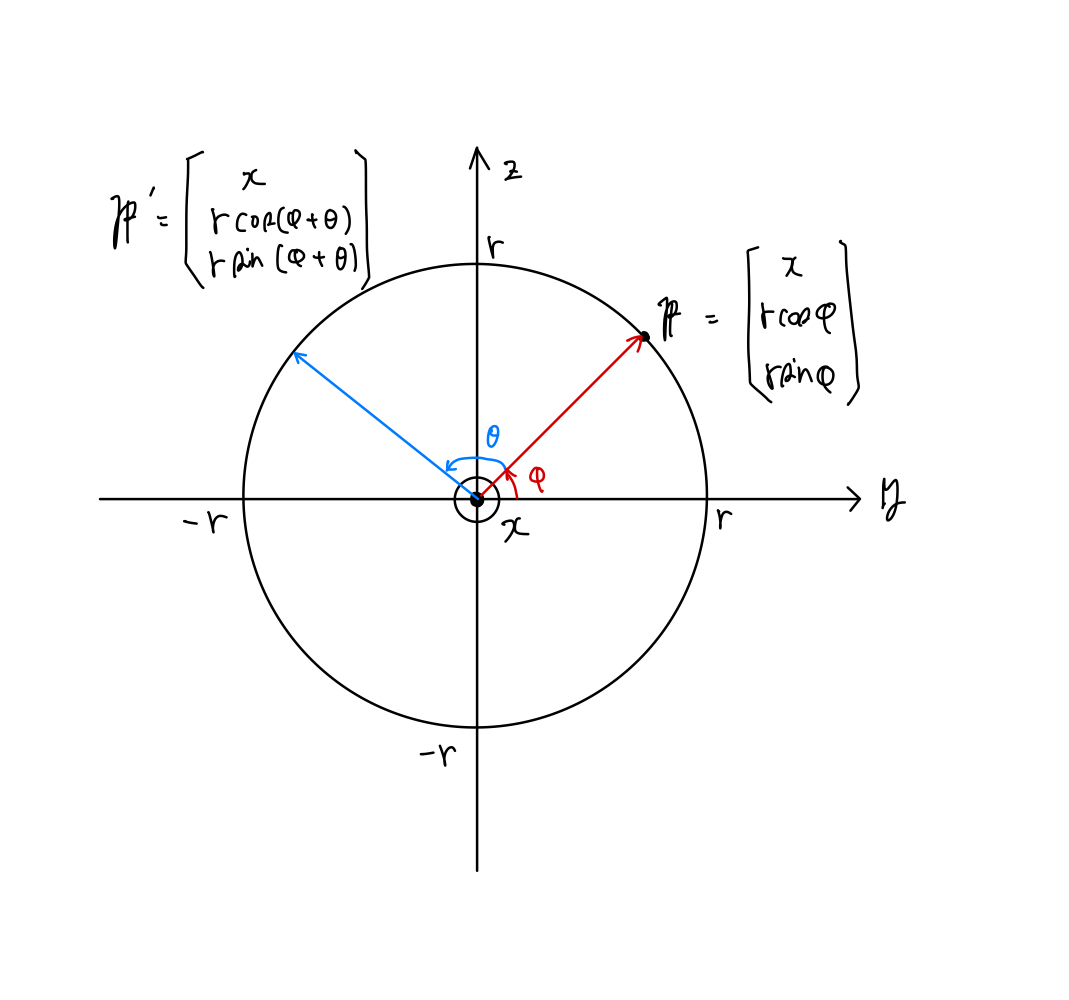
y-z平面の回転なので、ベクトル$p'$は以下で表すことができます。
⚠️y-z平面(x軸まわり)の回転のためx成分は不変

$$p' = \begin{bmatrix} x \\\\ r\cos(\phi + \theta) \\\\ r\sin(\phi + \theta) \end{bmatrix}$$

と表すことができます。ここで加法定理より

$$\cos(\phi + \theta) = \cos\phi\cos\theta - \sin\phi\sin\theta \\ \sin(\phi + \theta) = \sin\phi\cos\theta + \cos\phi\sin\theta$$

となるので、ベクトル$p'$を変形して以下で表すことができます。

$$p' = \begin{bmatrix} x \\\\ r(\cos\phi\cos\theta - \sin\phi\sin\theta) \\\\ r(\sin\phi\cos\theta + \cos\phi\sin\theta) \end{bmatrix} = \begin{bmatrix} x \\\\ y\cos\theta - z\sin\theta\ \\\\ y\sin\theta + z\cos\theta\ \end{bmatrix}$$

同次座標系にするために4x4行列に拡張すると、x軸回転行列は以下で表すことができます。

$$R_x= \begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & \cos\theta & -\sin\theta & 0 \\ 0 & \sin\theta & \cos\theta & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix}$$

---

y軸回転行列

y軸を中心に回転する場合、x–z平面上の点が円を描きます。
yの値は変わらず、xとzが角度 $\theta$ に応じて変化します。
導出はx軸回転行列に対して、回転軸を変えるだけなので省略します。

$$R_y= \begin{bmatrix} \cos\theta & 0 & \sin\theta & 0 \\ 0 & 1 & 0 & 0 \\ -\sin\theta & 0 & \cos\theta & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix}$$

---

z軸回転行列

z軸を中心に回転する場合、x–y平面上の点が円を描きます。
zの値は変わらず、xとyが角度 $\theta$ に応じて変化します。
導出はx軸回転行列に対して、回転軸を変えるだけなので省略します。

$$R_z= \begin{bmatrix} \cos\theta & -\sin\theta & 0 & 0 \\ \sin\theta & \cos\theta & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix}$$

3.5 表現行列の合成

線形写像の合成は、表現行列の積に対応しています。
例えばx, y, z方向にそれぞれ0.5, 1.0, 2.0倍に拡大し、x方向に3000px, y方向に4000px平行移動し、x軸方向に$\pi/4$だけ回転する行列は以下で表せます。
⚠️本来平行移動は無次元だが、簡単のためpx単位に変換
⚠️行列は右側から作用することに注意

$$M \;=\; R_x|_{\theta=\tfrac{\pi}{4}}\; \cdot\; T\big|_{t_x=3000,\; t_y=4000,\; t_z=0}\; \cdot\; S\big|_{s_x=0.5, s_y=1.0, s_z=2.0}$$

4. WebGLを実際に動かす

3.5節で示した行列$M$を使った座標変換を実際に行います。

4.1 初期設定

まず風景画像を配置します。
モデルは4つの頂点からなる板ポリ、つまり2枚の三角形ポリゴンです。
モデルデータの生成と表示（頂点やポリゴン定義など)については本記事では割愛します。
例として、「拡大→平行移動→回転」の順で体験してみましょう。
⚠️行列の積は非可換なので、作用させる順番が変わると結果が変わることに注意

4.2 拡大行列を作用

まず4.1のモデルに、x, y, z方向にそれぞれ0.5, 1.0, 2.0倍に拡大する拡大行列$S\big|_{s_x=0.5, s_y=1.0, s_z=2.0}$を作用させます。

画像からもわかるように以下が観察できました！

• x軸(横幅):0.5倍に縮小 → モデルが横に細くなる
• y軸(高さ): 1.0倍で変化なし → 高さはそのまま
• z軸(奥行き): 2.0倍に拡大 → 2Dモデルでは直接見えないが、三次元空間での奥行きが拡大される

4.3 平行移動行列を作用

同様に4.2のモデルに、x方向に3000px, y方向に4000px平行移動する平行移動行列$T\big|_{t_x=3000,\; t_y=4000,\; t_z=0}$を作用させます。

画像からもわかるように以下が観察できました！

• x軸方向: 3000px → モデルが右に移動
• y軸方向: 4000px → モデルが上に移動
• z軸方向: 0px → 奥行きは変化なし

4.4 回転行列を作用

同様に4.2のモデルに、x軸方向に$\pi/4$だけ回転する回転行列$R_x|_{\theta=\tfrac{\pi}{4}}$を作用させます。

画像からもわかるように、モデルの上部が奥側に、下部が手前側に傾きます

4.5 合成した表現行列を作用

いよいよ本題です。4.2-5は一つの行列の積を考えていましたが、最後に式3.5の表現行列$M$を作用させます。(x, y, z方向にそれぞれ0.5, 1.0, 2.0倍に拡大し、x方向に3000px, y方向に4000px平行移動し、x軸方向に$\pi/4$だけ回転する)

このように行列を作用させることで、座標変換を行うことができます。

5. 円形カルーセルを作成

前置きが長くなりましたが、いよいよ本題です！
これまでは行列を使った座標変換の基礎を学びました。
ここからは実際に複数枚の画像(モデル)を配置してカルーセルを作成していきます。

今回は以下の3種類のカルーセルを作成しました。

• 直線カルーセル: カードを一列に並べ、中央を手前に
• 水平カルーセル: y軸周りに円形配置
• 垂直カルーセル: z軸周りに円形配置

5.1 共通の設定

3種類のカルーセルの共通設定

• カード間の距離: 各カードは3000px分の間隔で配置
• 無限スクロール: ボタンでモデルが左右に移動し、ループ処理により端に到達したカードは反対側から再び現れる
• 14枚のカード: 14枚の画像を円周上または直線上に配置

5.2 直線カルーセル

最もシンプルなカルーセルです。14枚のカードを横一列に等間隔で並べます。
中央に来たモデルを強調するために、拡大します。
画面中央(x = 0)からの距離で判定し、最も距離が近いモデルに対して平行移動行列を使ってz方向に移動します。
このとき滑らかに変化させるために、sin関数をイージング関数として使用しました。
https://x.com/YuYamada_opt/status/1982464085716586974

5.3 水平カルーセル

水平カルーセルでは、水平方向に複数のモデルを円状に並べ、それぞれのカードが常に正面を向くように配置します。
y軸を中心に円を描くようにカードを並べることで、横に広がる見え方を実現します。
https://x.com/YuYamada_opt/status/1982464705496256731

モデルの位置:円周上に配置

• 1枚あたりの角度は約 25.7°(=360° ÷ 14)になる
• 正面のカード(θ=0°)は円の手前(z方向)に配置される
• 右に行くほど x方向に動きz方向に奥へ回り込んでいくように配置する

モデルの向き: 常に正面を向く

モデルを円の外周に沿って並べただけだと、それぞれが外側を向いてしまいます。
そこで各モデルをy軸まわりに$-{\theta}$回転させて、正面方向(接線方向)に向かせます。

中央を拡大

正面のカードだけを3倍大きく表示して、立体感を表現します。ここでも5.2と同様にイージング関数を用いてカードの角度に応じて滑らかに拡大することで、中央のカードが自然に浮き上がるような表現をします。

行列で表現

この一連の変換は以下の行列積で表されます。

$$M(\theta) = T_{\text{center}} \cdot T_{\text{circle}}(\theta) \cdot R_y(-\theta) \cdot S(\theta)$$

各行列の意味は

1. $S(\theta)$：拡大して中央を強調
2. $R_y(-\theta)$：y軸回転させてモデルを正面に向ける
3. $T_{\text{circle}}(\theta)$：モデルをx方向へ円周上に配置
4. $T_{\text{center}}$：円全体を手前に寄せて、画面中央に表示

この順番で行列を掛け合わせることで、モデルは「拡大 → 向き合わせ → 配置 → 中央寄せ」という順で整列していきます。

5.4 垂直カルーセル

垂直カルーセルでは、垂直方向に複数のモデルを円状に並べ、z軸を中心に回転させることで、上下に回り込むような動きを実現します。
水平カルーセル（y軸回転）との違いは、回転軸と円の向きです。
水平ではy軸のまわりに円を描きましたが、垂直ではz軸を中心に円を描きます。
https://x.com/YuYamada_opt/status/1982464960547709038

モデルの位置:円周上に配置

5.3の軸を変えただけなので、詳細は省略します。

モデルの向き: 常に正面を向く

5.3の軸を変えただけなので、詳細は省略します。

中央を拡大

5.3と同じロジックで拡大率を変えただけなので、詳細は省略します。

行列で表現

この一連の変換は以下の行列積で表されます。

$$M(\theta) = T_{\text{center}} \cdot R_z(-\theta) \cdot T_{\text{circle}}(\theta) \cdot R_x(\pi) \cdot S(\theta)$$

各行列の意味は

1. $S(\theta)$：拡大して中央を強調
2. $R_x(\pi)$: 裏返り防止のため上下反転
3. $T_{\text{circle}}(\theta)$: モデルをy方向へ円周上に配置
4. $R_z(-\theta)$: z軸回転でカードを正面に向ける
5. $T_{\text{center}}$: 円全体を上に寄せて、画面中央に表示

この順番で行列を掛け合わせることで、モデルは「拡大 → 反転 → 円周配置 → 向き合わせ → 中央寄せ」という順で整列していきます。

水平と垂直の比較

項目	水平カルーセル	垂直カルーセル
回転軸	y軸	z軸
並び方向	左右方向	上下方向
円の平面	x–z平面	y-z平面
正面カード	z方向に手前	y方向に上側
見え方	横に回転するステージ	縦に回転する観覧車

6. まとめ

本記事では、WebGLと行列演算を使ったカルーセルUIの実装について解説しました。
感想としては、WebGL楽しいけどすごく難しかったです...

質問や感想等ございましたら、Xアカウントまでお願いします！