【三体問題#3】 実際に軌道伝播してみた

投稿の目的

一つ前の投稿の続きとして、軌道力学における三体問題を扱う。軌道力学における三体問題は、人口衛星(3つ目の天体)の運動が他の二つの天体（例えば地球と、月）の万有引力によって決定される力学モデルを表す。この投稿では、実際に運動方程式を立式して数値計算することで、三体問題の非線形性について紹介することを目的とする。

円制限三体問題 (CRTBP) の立式

本投稿では前回に引き続き、三体問題のうち、円制限三体問題を扱う。円制限三体問題の立式については、前回の投稿も参考にしていただきたい。
https://zenn.dev/soyster/articles/1f1d0b41dc8f7f
さて、運動方程式を二つの天体の共重心から見た回転座標系で記述すると、以下のようになる。

$$\begin{align*} \ddot{x}-2\dot{y}-x &= -\frac{(1-\mu)(x+\mu)}{r_1^3}-\frac{\mu(x-1+\mu)}{r_2^3}\\ \ddot{y}+2\dot{x}-y &= -\frac{(1-\mu)y}{r_1^3}-\frac{\mu y}{r_2^3}\\ \ddot{z} &= -\frac{(1-\mu)z}{r_1^3}-\frac{\mu z}{r_2^3}\\ \end{align*}$$

まずはこの運動方程式を実装し、実際に軌道計算を行う。今回は"Julia"言語を用いる。数値計算のライブラリが豊富なプログラムミング言語であるが、高速計算も可能な言語である。筆者はMATLABでの実装は経験があるが、Juliaは大学の時に少しだけ触った程度なので、思い出しがてら実装してみる。

https://julialang.org/
実際に実装した円制限三体問題の運動方程式の関数スクリプトは以下である。この際、JAXA (宇宙科学研究所) の方のZennの記事を参考にさせていただいた。
https://zenn.dev/naoyaozaki/articles/a3c0b199cdf23f

#EQUATION OF CIRCULAR RESTRICETED THREE-BODY PROBLEM 
function eom_crtbp!(dx,x,µ,t)
	r1 = x[1:3] + [µ,0,0]
	r2 = x[1:3] - [1-µ,0,0]
	a_cori = [2x[5],-2x[4],0]
	a_cf = [x[1],x[2],0]
	dx[1:3] = x[4:6]
	dx[4:6] = -(1-µ)*r1/(norm(r1)^3)-µ*r2/(norm(r2)^3) + a_cori + a_cf
end

しかし、かつて言及したが、この問題は解析的には解けず数値的にしか値が求められないので、軌道を設計するためには初期値が非常に重要である(制御しない限り、天体の質量と初期値によって軌道はほぼ決まると言っても良い)。ここでは初期値を少し変えるだけで軌道が全く異なることを紹介する。

初期値1

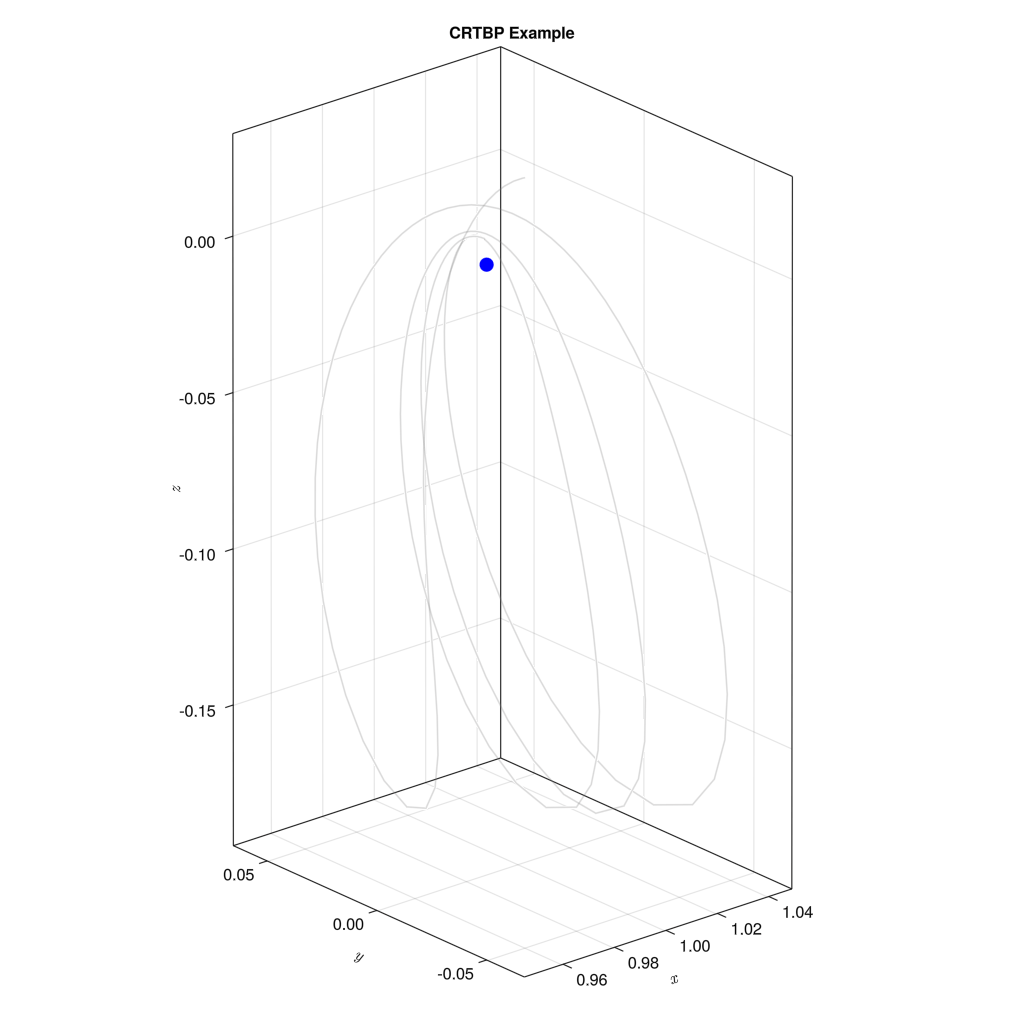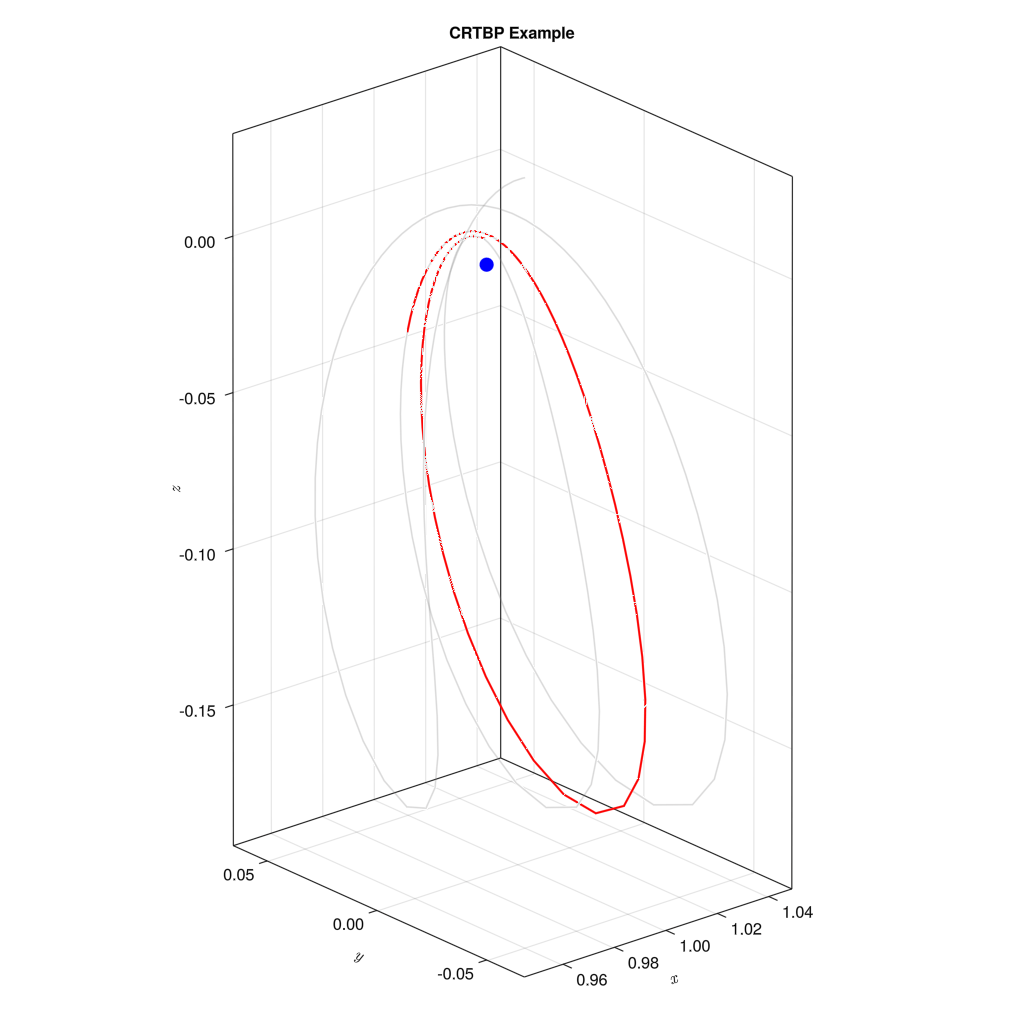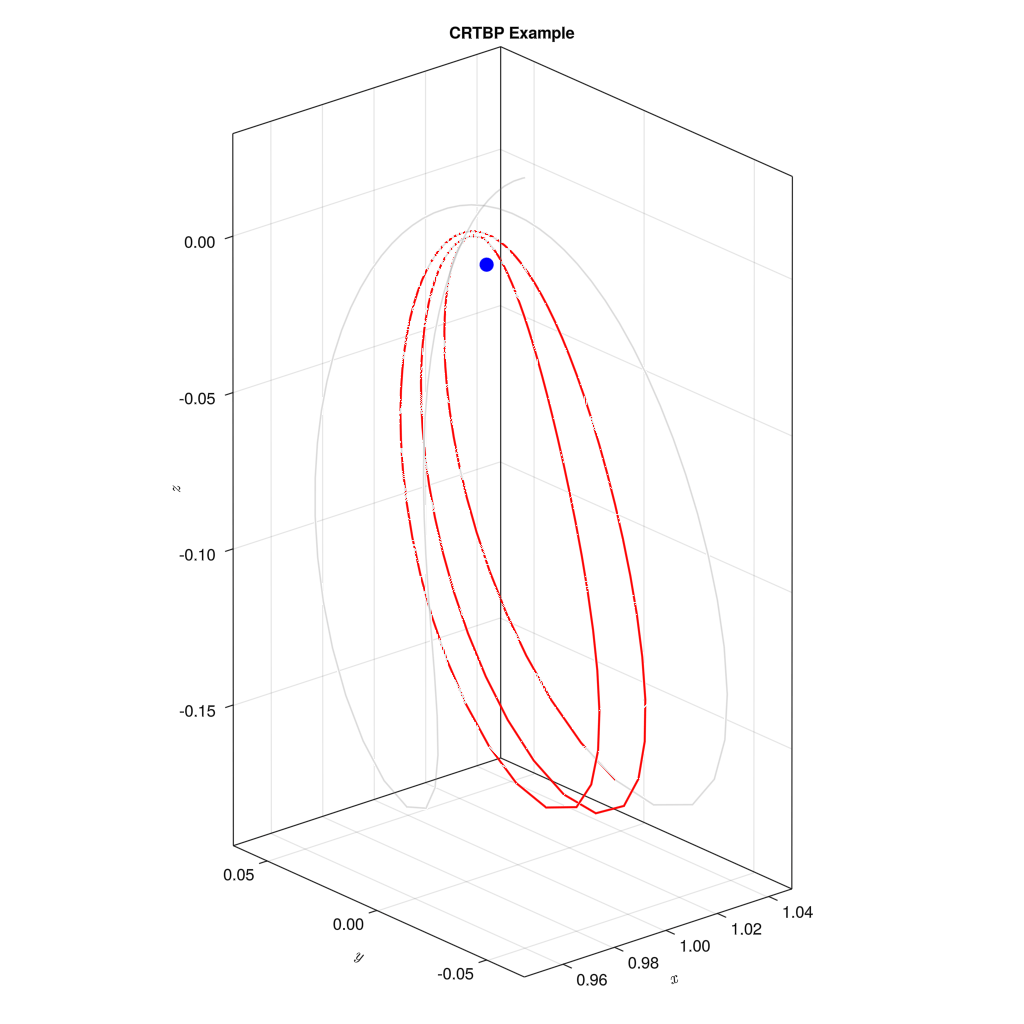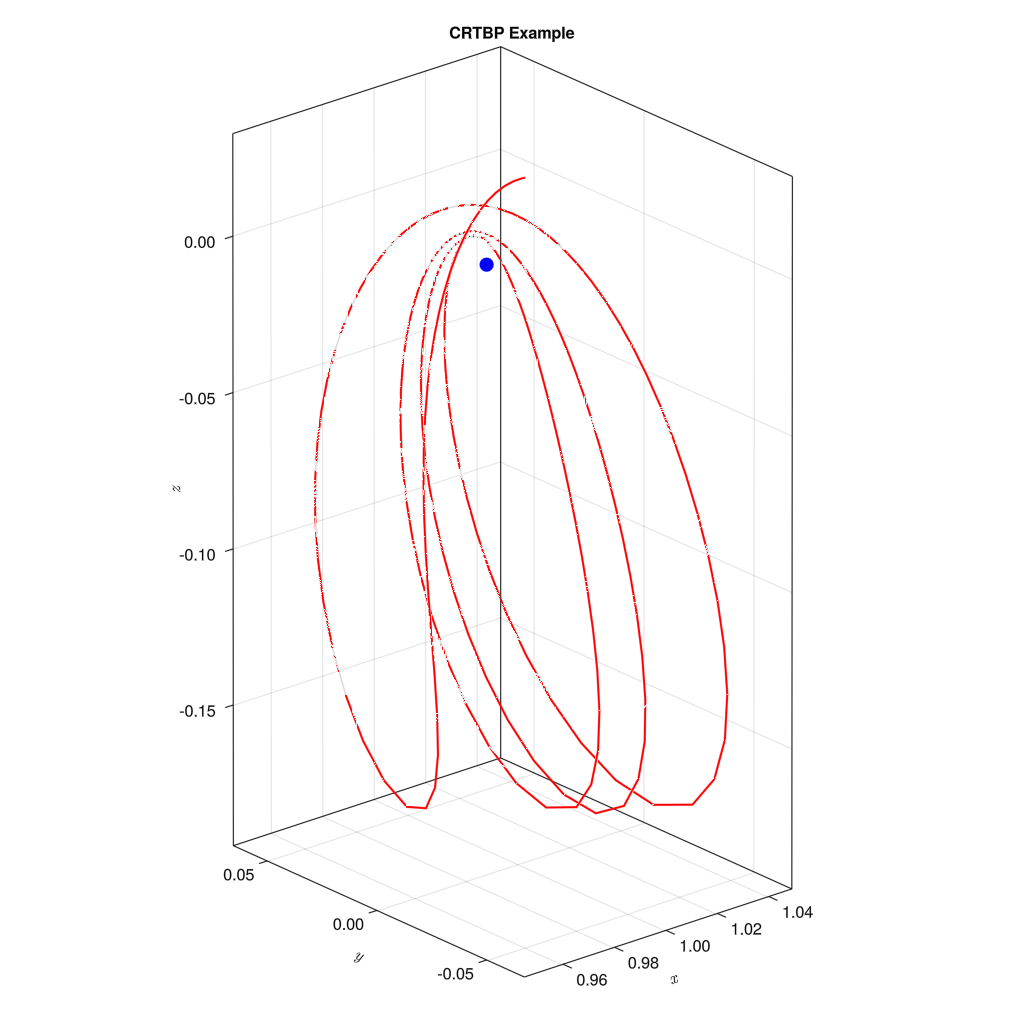
なお、プロット上の青い点は第二天体 (ここでは月)を表す。

x0 = [0.987384153663276, 0.0, 0.008372273063008, 0.0, 1.67419265037912, 0.0]

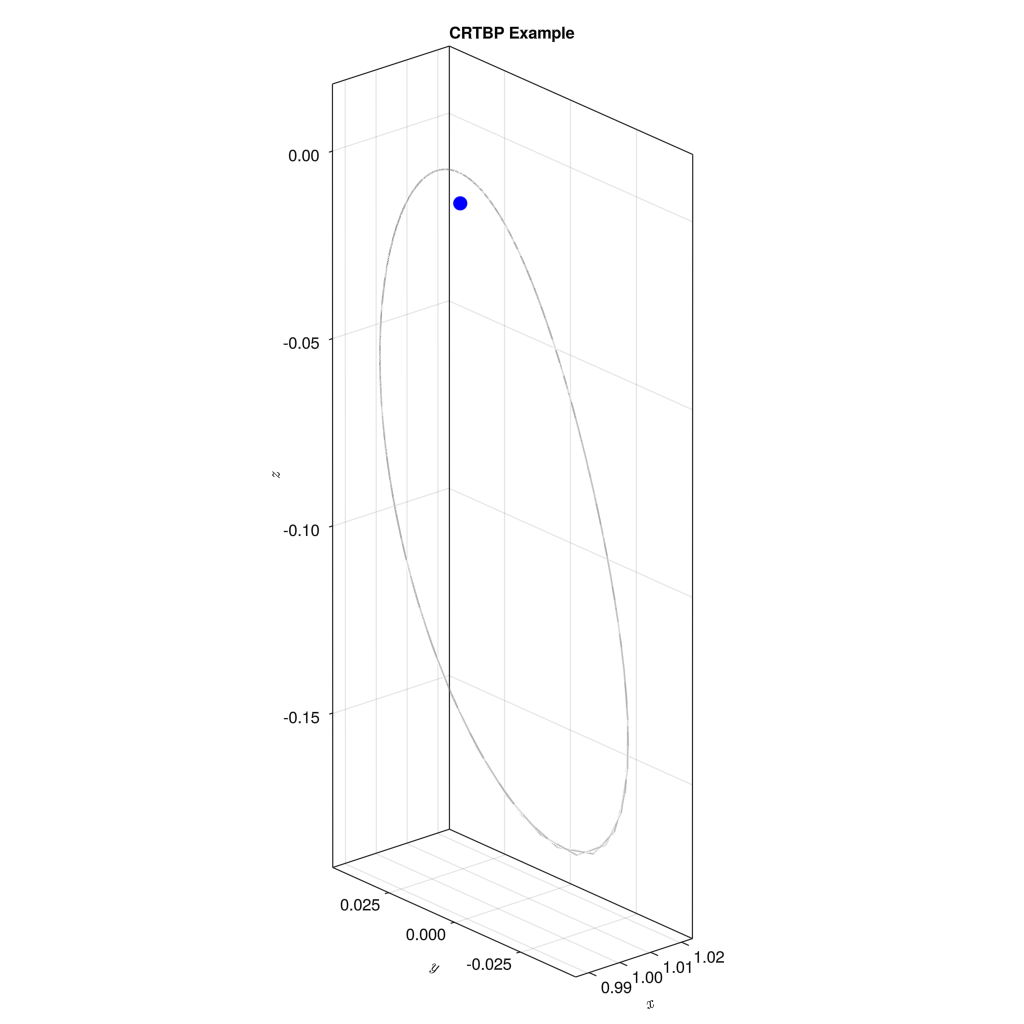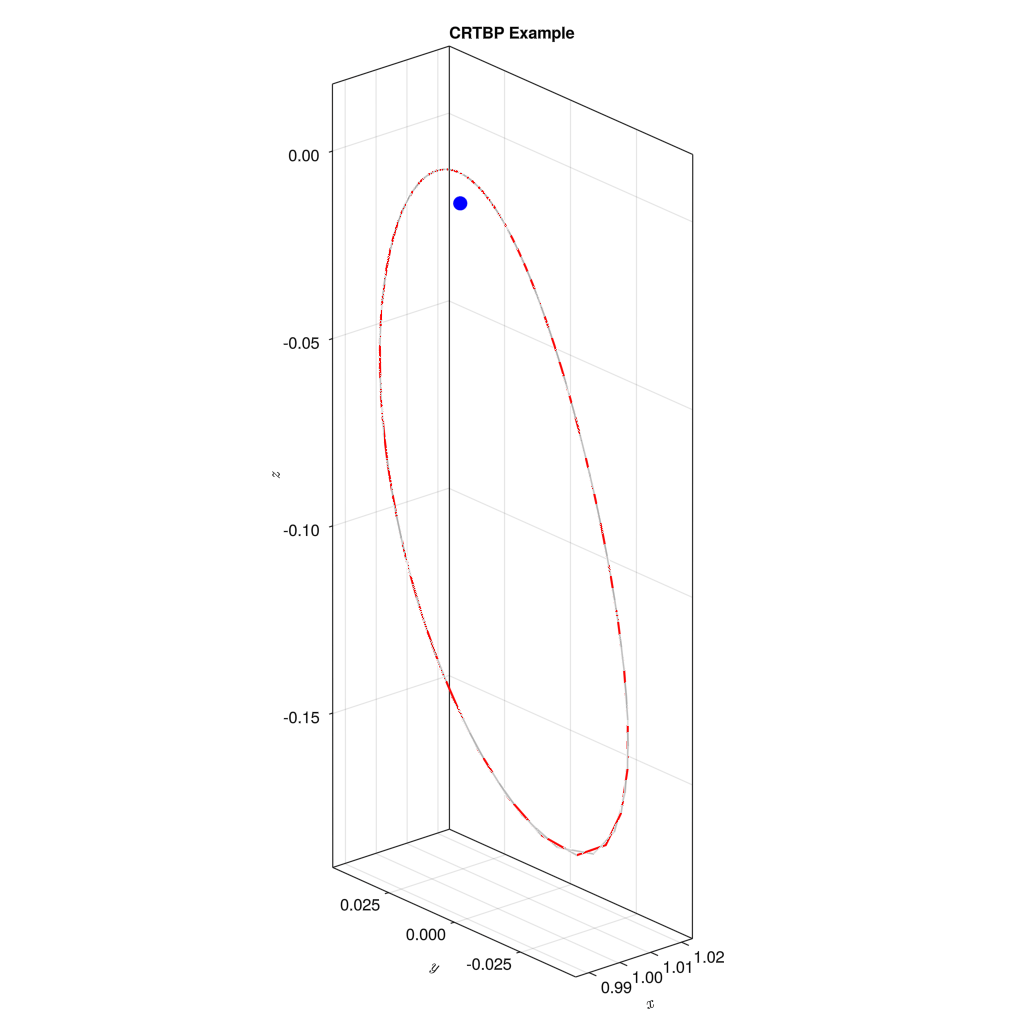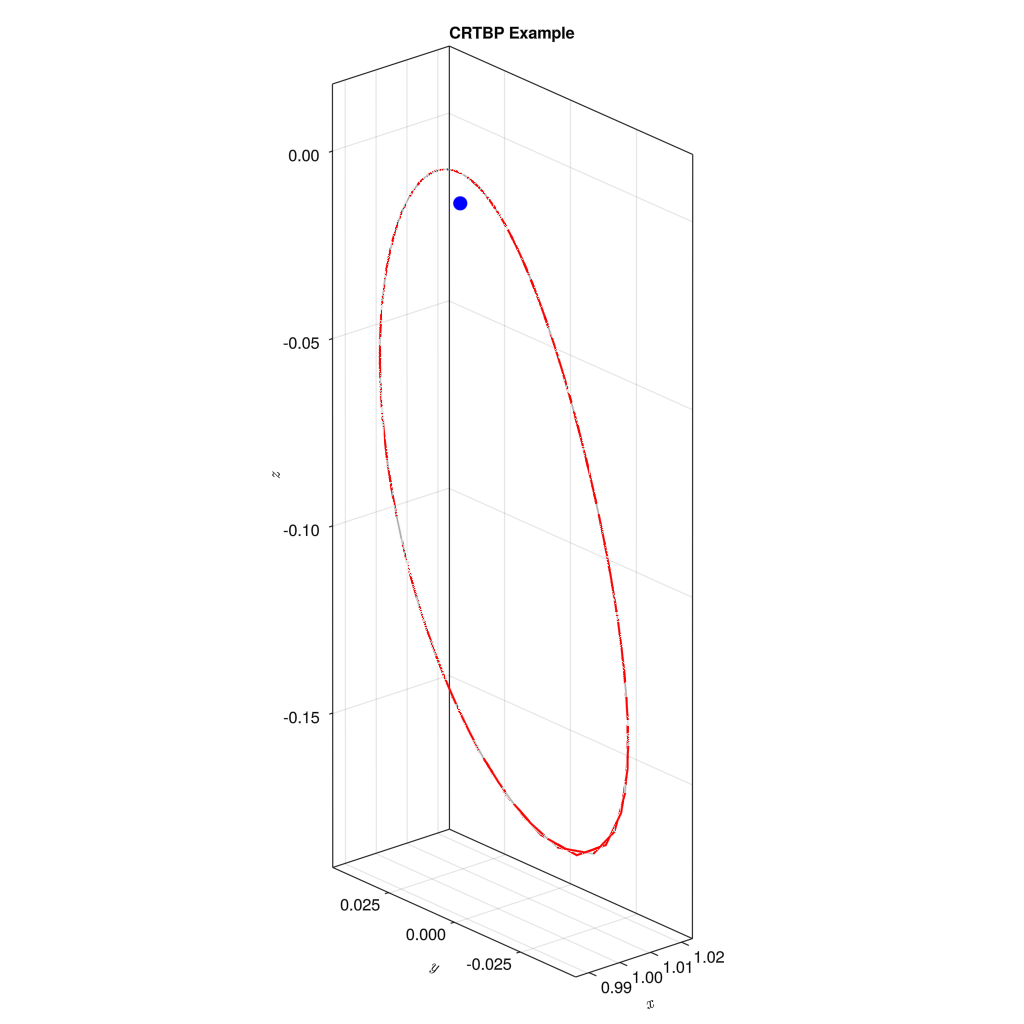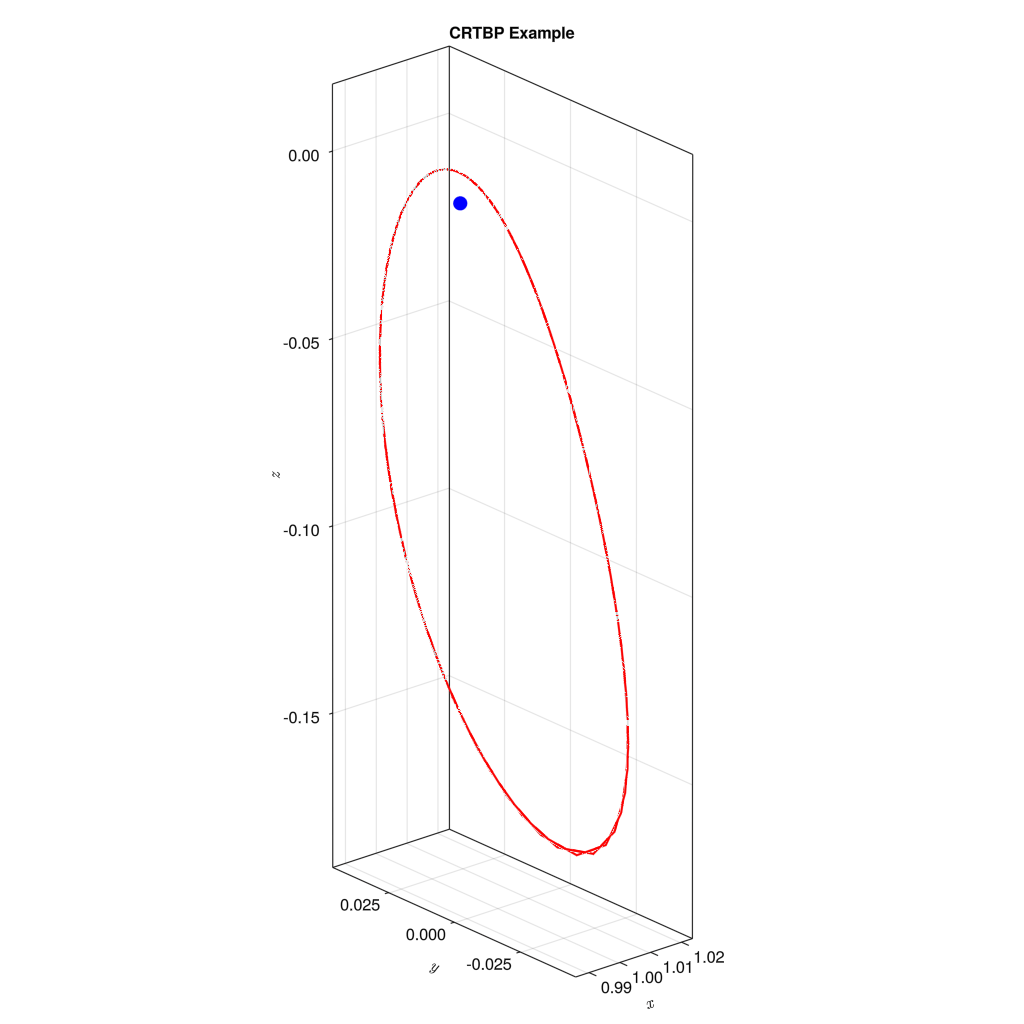
初期値2

少しだけ、値を変えてみる。$x$の値が$1e-4$のオーダーで異なる。

x0 = [0.987284153663276, 0.0, 0.008372273063008, 0.0, 1.67419265037912, 0.0]

比較結果に対するコメント

結果は上記の通りである。初期値を少し変えるだけで、初期値1のような安定した軌道から、少しずれたような軌道へ変化する。ちなみに、「この初期値を使えば比較的安定した軌道が描けますよ」というのをNASAが提供してくれているデータベースが存在する。
https://ssd.jpl.nasa.gov/tools/periodic_orbits.html

本投稿のまとめ

今回は、以前までに紹介した円制限三体問題を実装してJulia言語で描画してみた。Julia言語にまだあまり慣れていないが、実際に計算できると楽しいので、引き続き遊んでみる。